План лекций: Введение Ценные бумаги (акции, облигации) Рынок денег Товарный рынок

Вид материала

Анализ

Содержание Оценивание облигаций» Требуемая доходность (required yield)

Подобный материал:

• Лекция. Основные понятия фондового рынка. Фондовый рыно, 82.73kb.
• Облигации как объект инвестиций, особенности инвестиций в облигации, 1796.25kb.
• Список вопросов к экзамену по курсу, 30.12kb.
• Рынок финансовых услуг сущность, функции и структура рынка финансовых услуг, 449.67kb.
• Курс лекций по дисциплине «Рынок ценных бумаг» Составитель: к э. н., доцент Бобылев, 258.71kb.
• Программа дисциплины «Неэмиссионные ценные бумаги», 279.64kb.
• В число которых не входят сами ценные бумаги, 207.91kb.
• Вопросы для подготовки к тестированию по курсу «Рынок ценных бумаг», 148.48kb.
• «Учет финансовых вложений в акции и долговые ценные бумаги». Научный Березина, 249.1kb.
• Ценные бумаги, 780.7kb.

ОБЛИГАЦИИ.

Облигации относятся к группе ценных бумаг, которые являются инструментами займа , т.е. это долговые ценные бумаги , подтверждающие обязательство эмитента выплачивать фиксированный процент в течение определенного периода и возвратить основную сумму при наступлении срока погашения .


Основой этого рынка являются государственные ценные бумаги, выпускаемые на значительный срок, например, 30 лет, для покрытия дефицита государственного бюджета. К ним также относят муниципальные и корпоративные облигации. Долговые обязательства являются исключительно надежным финансовым инструментом, однако их доходность невысока.


Фундаментальными свойствами облигаций являются:


- отношения займа между инвестором и эмитентом. Лицо, приобретающее

облигацию, не становится совладельцем предприятия, а является его

кредитором;

• наличие конкретного срока обращения облигации, по истечении которого она погашается, т.е. выкупается эмитентом по номинальной стоимости;
  
• приоритет облигаций по сравнению с акциями в получении дохода. Выплата процентов по облигациям производится в первоочередном порядке по сравнению с выплатой дивидендов по акциям;
  
• наличие у владельца облигации права на первоочередное удовлетворение его требований по сравнению с акционером при ликвидации его предприятия.
  

Оценивание облигаций»

Оценивание облигаций

Цена любого финансового инструмента равна текущей стоимости ожидаемого денежного потока от этого финансового инструмента. Таким образом, для определения цены необходимо:

1. Оценить ожидаемый денежный поток.
   
2. Оценить соответствующую требуемую доходность.
   

Ожидаемые денежные потоки некоторых финансовых инструментов вычислить просто, для других это сделать сложнее. Требуемая доходность (required yield) является оценкой доходности финансовых инструментов со сравнимым риском, т.н. альтернативных инструментов.

Первым шагом в вычислении цены облигации является определение ее денежного потока. Денежный поток для облигации, которую эмитент не может отозвать до установленной даты погашения, т.е. неотзывной облигации состоит из:

1. Периодических купонных выплат до даты погашения.
   
2. Выплаты номинала в дату погашения.
   

В нашей иллюстрации оценивания облигаций для упрощения будут сделаны три предположения:

1. Выплаты купона производятся каждые 6 месяцев. (Для большинства облигаций в США купонный процент действительно выплачивается раз в полгода.)
   
2. Следующая выплата по облигации будет произведена ровно через 6 месяцев от настоящего момента.
   
3. Купонная ставка не изменяется в течение всего срока действия облигации.
   

рис. 1.

Поток платежей по облигации.


Следовательно, денежный поток неотзывной облигации состоит из ренты с фиксированными купонными платежами раз в полгода и выплаты номинала. Например, 20-летняя облигация с купонной ставкой 10% и номиналом $1 000 имеет следующие купонные платежи:

Годовой купон = $1 000  0,10 = $100

Полугодовой купон = $100 / 2 = $50

Таким образом, будет получено 40 полугодовых купонов по $50 и номинал $1000 через 40 полугодовых периодов от настоящего момента.

Отметим особенность временной привязки выплаты номинала. Вместо того, чтобы говорить о выплате номинала через 20 лет, говорят о его выплате через 40 купонных периодов.

Требуемая доходность определяется путем исследования доходностей, предлагаемых на рынке по сравнимым облигациям. В нашем случае сравнимыми инструментами могут быть неотзывные облигации с таким же инвестиционным качеством и той же датой погашения. Требуемая доходность обычно выражается в виде годовой процентной ставки. Если платежи поступают раз в полгода, на рынке принято соглашение использовать 1/2 годовой процентной ставки в качестве процентной ставки за купонный период, с помощью которой дисконтируются денежный поток.

Если известны денежные потоки и требуемая доходность, то мы обладаем всей информацией, необходимой для оценивания облигаций. Т.к. цена облигации – это текущая стоимость денежного потока, то она определяется путем сложения следующих двух значений:

1. Текущей стоимости полугодовых купонных выплат.
   
2. Текущей стоимости номинала (или суммы погашения).
   

Текущая стоимость облигации определяется приведением её денежного потока к начальному моменту времени. В роли ставки дисконтирования при этом выступает требуемая доходность. (см. рис. 2).



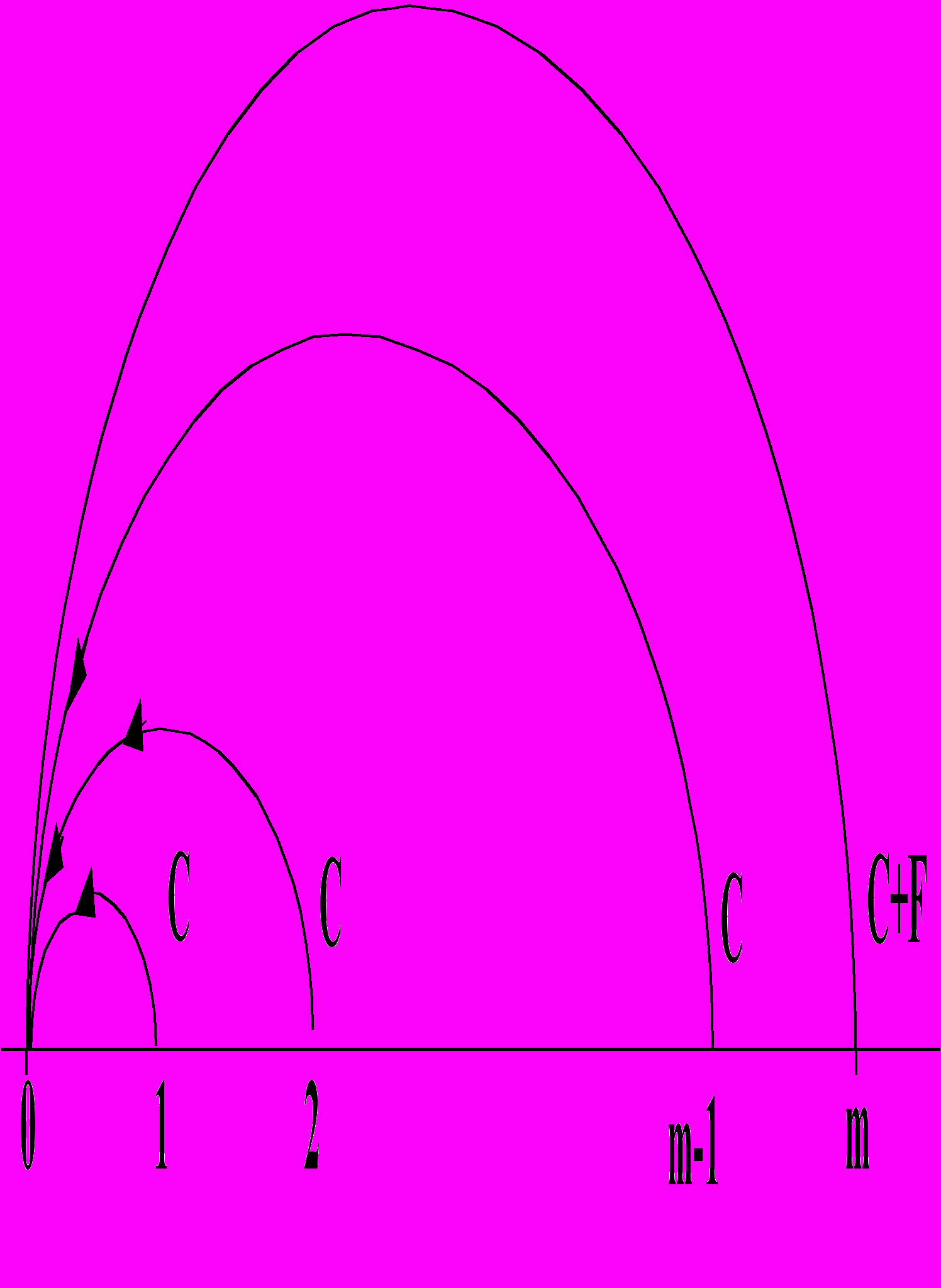
рис. 2

Дисконтирование потока платежей.


Если 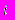- процентная ставка дисконтирования за купонный период, то внутренняя цена 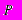облигации вычисляется по формуле: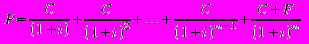





или




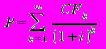
где P – цена (â $)

m – число купонных периодов (число лет * 2)

C – полугодовая купонная выплата (в $)

i – процентная ставка за купонный период (требуемая годовая доходность : 2)

F – сумма погашения

k – период времени, когда производится выплата

Поскольку полугодовые купонные выплаты эквивалентны обычной ренте, то их текущая стоимость может быть найдена по следующей формуле:


текущая стоимость купонных выплат = C(1/i-1/i(1+i)m)


Процентные ставки, с точки зрения инвестора, характеризуют эффективность или доходность инвестиций. Годовая процентная ставка показывает инвестору ожидаемый годовой доход на единицу инвестируемого капитала. Рыночная процентная ставка для заданного класса активов (например, облигаций) дает "усредненную" величину доходности активов этого класса. Заданный уровень процентных ставок (доходности) определяет стоимость облигаций, на которую можно смотреть как на оценку некоторой теоретической или, как еще говорят, внутренней цены облигации. Реальная рыночная цена, складывающаяся под взаимодействием спроса и предложения, зависит от множества различных факторов, как относящихся к самой облигации (срок погашения, купонная ставка и т. п.) так и внешним по отношению к ней (экономическая конъюнктура, уровень инфляции , налога, транзакционные издержки и т. п.). Как будет показано ниже, рыночная цена облигации в условиях "равновесного рынка" совпадает с ее стоимостью, реально она колеблется "вблизи" этого значения.

Можно показать, что если требуемая доходность равна купонной ставке (10%), то цена облигации будет равна ее номиналу ($1 000).

По бескупонным облигациям не производится никаких купонных выплат. В этом случае инвестор получает процентный доход как разность между суммой погашению и ценой покупки. Цена бескупонной облигации находится из уравнения (1) подстановкой нуля вместо C:

Р= F/(1+i)m (3)

Уравнение (3) утверждает, что цена бескупонной облигации – это просто текущая стоимость суммы погашения. Однако при вычислении приведенной стоимости число периодов, используемое для дисконтирования, не является числом лет до погашения облигации, а равна удвоенному числу лет. Несмотря на то, что по бескупонной облигации купонных выплат не осуществляется, её временные параметры измеряются тем же способом, что и для купонных облигаций. Это делается для соизмеримости вычисляемых доходностей. Ставка дисконтирования равна половине требуемой годовой доходности.


Соотношение цены и доходности