Geum.ru

Учебно-практическое пособие для студентов очной и заочной форм обучения с применением дистанционных образовательных технологий

Вид материалаУчебно-практическое пособие

Содержание


3.2. Закон самосохранения
Подобный материал:
1   ...   9   10   11   12   13   14   15   16   ...   28

3.2. Закон самосохранения


Закон самосохранения: любая организация, также как и её отдельный элемент, стремятся сохранить себя как единое целое.

Условия выполнения закона самосохранения формально принято записывать следующим образом [1]:


,


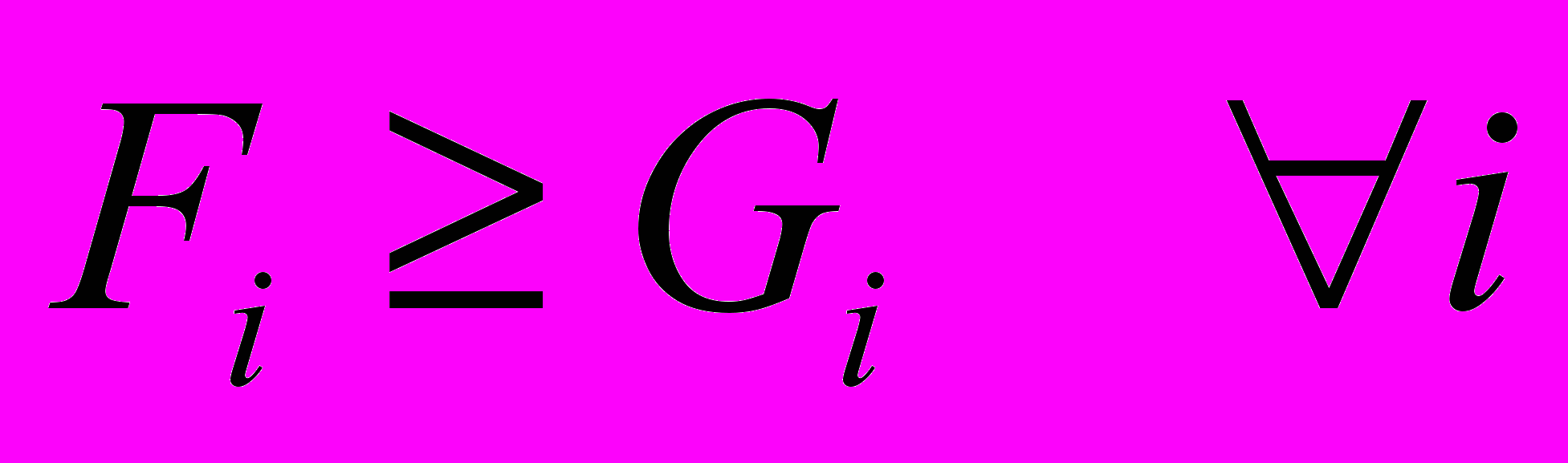где - потенциал (ресурс) организации в некоторой области деятельности i (для хозяйственных организаций могут рассматриваться разработки, производство, сбыт, финансы и т.п.); 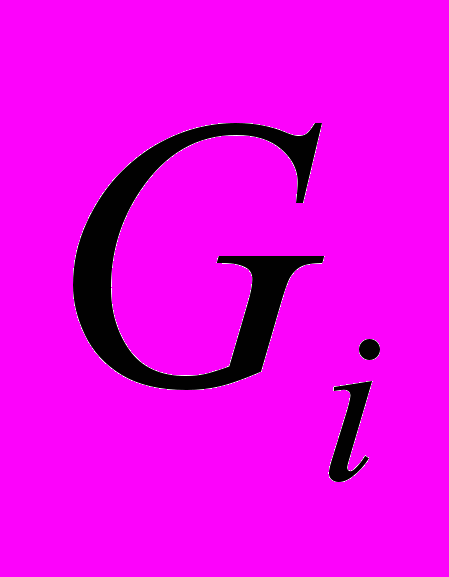- потенциал внешнего или внутреннего воздействия (например, действия конкурентов или оппонентов руководству), разрушающий или уменьшающий этот ресурс.

Закон самосохранения требует соблюдения организационной устойчивости. Организационная устойчивость – это способность организации противостоять разрушающим внешним воздействиям и неблагоприятным ситуациям, возникающим во внутренней среде организации.

Классификация видов устойчивости систем (организаций) впервые была предложена Богдановым. Согласно этой классификации принято различать два вида устойчивости: количественную и структурную [10] (в последнее время вместо термина структурная устойчивость часто используется термин системная устойчивость).

Количественная устойчивость прямо связана с числом элементов, входящих в состав организации. Рассмотрим пример, приведенный Богдановым.




Рис. 3.3. Иллюстрация понятия количественной устойчивости


На поверхности (рис. 3.3) расположены две капли жидкости, которые испаряются. Очевидно, что первой испарится меньшая капля. Вывод: организация, охватывающая большее количество элементов, более устойчива к воздействиям окружающей среды.

Положительный прогрессивный отбор ведет к возрастанию количественной устойчивости, отрицательный - к ее уменьшению. Для хозяйственных организаций эффект количественной устойчивости проявляется в виде действия масштабного фактора (например, организация, обеспечивающая больший объем производства, имеет преимущество).

Реальная устойчивость системы зависит не только от количества элементов, но и от способа их организационной связи, т.е. от структуры системы. Выражением структурной устойчивости является закон равновесия Ле-Шателье, сформулированный для систем равновесия – систем, сохраняющих своё строение (структуру) в данной среде.

Закон Ле-Шателье. Если система равновесия подвергается воздействию, изменяющему какое-либо из условий равновесия, то в ней возникают процессы, направленные так, чтобы противодействовать этому изменению.

Для живых организмов последний закон приводит к понятию гомеостазиса (гр. homoios – подобный и stasis - состояние). Гомеостазис – совокупность сложных приспособительных реакций организма, направленных на устранение или максимальное ограничение действия различных факторов внешней или внутренней среды, нарушающих относительное динамическое постоянство внутренней среды организма (например, постоянство температуры тела, кровяного давления и др.).

Структурная устойчивость всегда может быть выражена количественно. Так, в физике коэффициенты сопротивления разрыву, кручению и т.п. являются численным выражением структурной устойчивости разных тел по отношению к определенным внешним воздействиям. В то же время масса характеризует количественную устойчивость этих тел.

Структурная устойчивость зависит от однородности организационных связей. Для обоснования этого тезиса, Богданов сформулировал закон «наименьших сопротивлений»:

Закон наименьших сопротивлений. Устойчивость целого зависит от наименьших сопротивлений всех его частей в каждый момент времени.

Суть этого закона тривиальна и сводится к известной русской пословице: «где тонко, там и рвется». Иными словами: разрушение структуры организации начинается с наименее сильных связей. Отсюда вывод: если все связи однородны, то нет и «слабого звена».

Возрастание однородности структуры системы приводит к возрастанию её структурной устойчивости и наоборот, возрастание неоднородности структуры чревато снижением структурной устойчивости. Отрицательный прогрессивный отбор, приводящий к увеличению однородности структуры, одновременно приводит к увеличению структурной устойчивости системы. Наоборот, положительный прогрессивный отбор ведет к возрастанию неоднородности структуры и, как следствие, к снижению структурной устойчивости. Отсюда следует вывод о существовании предела роста любой организации. При превышении этого предела нарушается структурная устойчивость организации и происходит ее разрушение.

Интересный результат, касающийся устойчивости систем, получен Джоном Клиром [18]. Его идея состояла в следующем: численные зависимости устойчивости системы от её размера (числа элементов) и её связанности (числа зависимостей между элементами), являющейся характеристикой структуры, могут быть получены в результате компьютерных экспериментов. В результате был открыт следующий статистически достоверный закон: если динамическая система достаточно велика (содержит 10 и более переменных) и её связанность меньше 13% (критическая связанность), тогда система почти наверняка устойчива. Если её связанность больше 13% , она почти наверняка неустойчива; 2% отклонения от критической связанности оказывается достаточным для того, чтобы ответ на вопрос об устойчивости из «почти наверняка устойчива» превратился в «почти наверняка неустойчива». Зависимость вероятности устойчивости системы 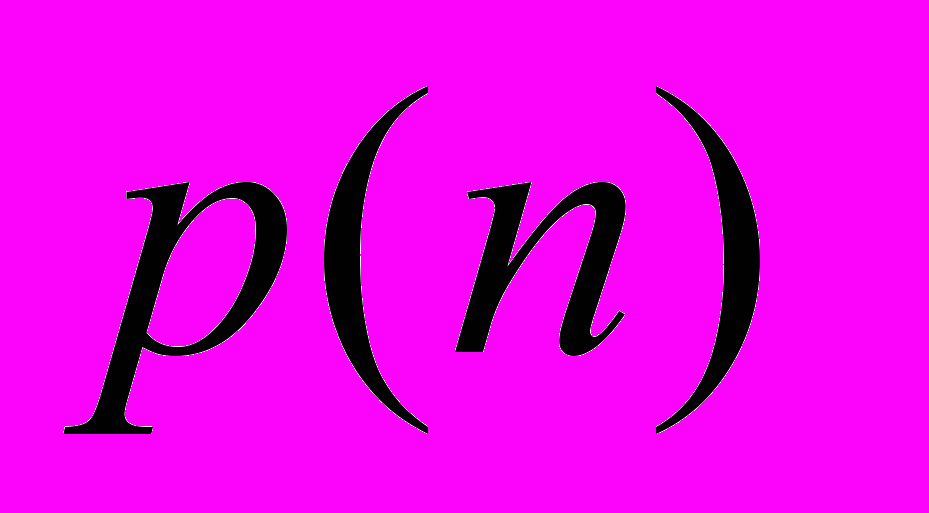от числа её элементов n имеет вид:


.


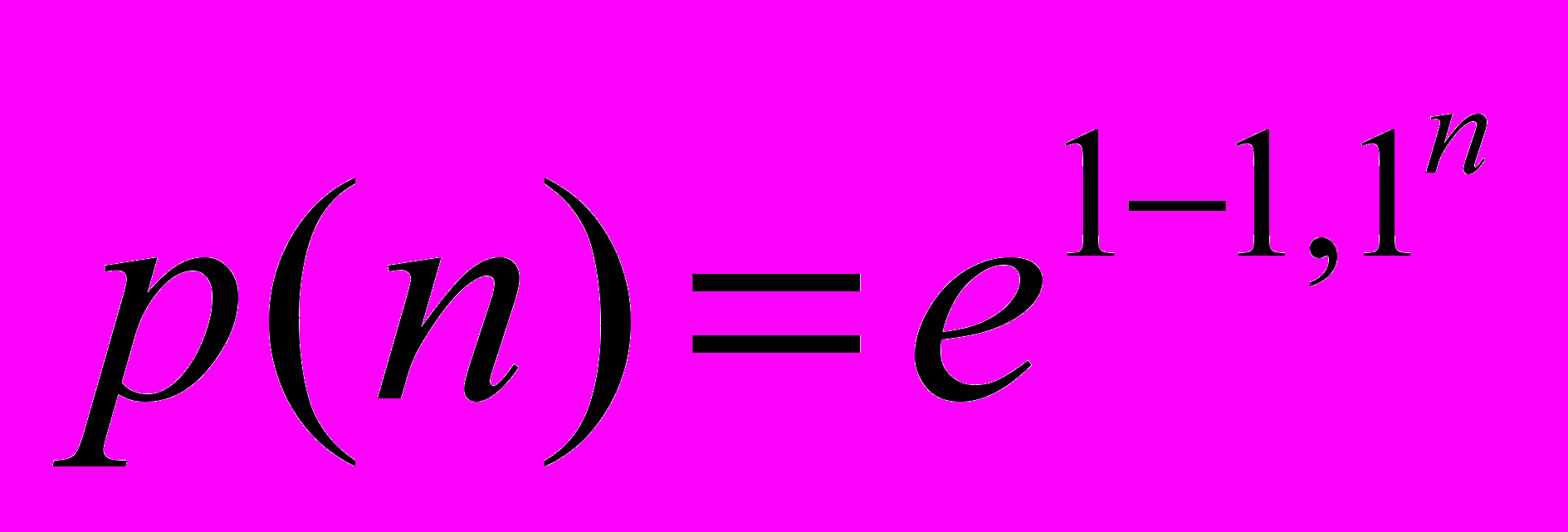В силу значительного количества проведенных вычислений приведенное выше соотношение можно рассматривать как общий закон устойчивости систем.