Учебно-методический комплекс для студентов очной и заочной форм обучения по специальностям 080105. 65 «Финансы кредит» (по циклу дисциплин ен. В. 01а)

Вид материала

Учебно-методический комплекс

Содержание Цель преподавания Учебно-тематические планы занятий Наименование темы Учебно-тематический план занятий Наименование темы 2 Учебная программа дисциплины Тема 2. Математическое программирование, его место Тема 3. Экономическая динамика. Примеры моделей Тема 4. Математические модели оптимальных процессов Тема 5. Дискретные процессы. Динамическое программирование Тема 6. Задача оптимального управления для непрерывных Тема 7. Метод вариационного исчисления и его применение Тема 8. Методы статистического моделирования и их применение Тема 9. Математические методы принятия решений в условиях Тема 10. Принятие решений в условиях конфликта Тема 11. Теория графов. Сетевые модели Тема 12. Методы и модели массового обслуживания Тема 13. Многокритериальная оптимизация 3 Список литературы 4 Планы практических занятий ... Полное содержание

Подобный материал:

• Учебно-методический комплекс для студентов очной и заочной формы обучения по специальностям:, 565.24kb.
• Учебно-методический комплекс по циклу дисциплин гсэ. В. 01а для студентов очной (заочной), 610.27kb.
• Учебно-методический комплекс по циклу дисциплин сд. 04 Для студентов очной и заочной, 382.23kb.
• Учебно-методический комплекс для студентов очной и заочной формы обучения по специальностям:, 340.96kb.
• Учебно-методический комплекс для студентов очной и заочной формы обучения по специальностям:, 412.98kb.
• Учебно-методический комплекс для студентов очной и заочной формы обучения по специальностям:, 422.73kb.
• Учебно-методический комплекс для студентов очной и заочной формы обучения по специальностям:, 434.06kb.
• Учебно-методический комплекс для студентов заочной формы обучения по специальностям:, 287.37kb.
• Учебно-методический комплекс для студентов очной формы обучения по специальностям:, 250.32kb.
• Учебно-методический комплекс по циклу дисциплин гсэ. Ф. 08 Для студентов очной формы, 440.95kb.

НЕГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«КУЗБАССКИЙ ИНСТИТУТ ЭКОНОМИКИ И ПРАВА»

ЭКОНОМИЧЕСКИЙ ФАКУЛЬТЕТ

КАФЕДРА МАТЕМАТИЧЕСКИХ И ЕСТЕСТВЕННОНАУЧНЫХ ДИСЦИПЛИН

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ

МЕТОДЫ

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС

для студентов очной и заочной форм обучения

по специальностям

080105.65 - «Финансы кредит» (по циклу дисциплин ЕН.В.01а)

080502.65 - «Экономика и управление на предприятии

(информационные технологии и связь)» (по циклу дисциплин ЕН.В.02а)

080503.65 - «Антикризисное управление» (по циклу лисциплин ЕН.Ф.03)

КЕМЕРОВО 2007

Экономико-математические методы: учебно-методический комплекс для студентов очной и заочной форм обучения / сост. В. А. Чекменев; Кузбас. ин-т зкон. и права. – Кемерово, 2007. – 24 с.


Настоящий учебно-методический комплекс разработан в соответствии с Государственным образовательным стандартом высшего профессионального образования по специальностям – 060400 (080105.65) «Финансы и кредит», квалификация – экономист; 060800 (080502.65) «Экономика и управление на предприятии (в информационных технологиях и связи)», квалификация - экономист-менеджер;351000 (080503.65) «Антикризисное управление», квалификация – экономист-менеджер.


УМК содержит все необходимые для изучения и преподавания курса «Экономико-математические методы» учебно-методические материалы; предназначен для студентов очной и заочной формы обучения экономического факультета института.


Утвержден на заседании кафедры математических и естественнонаучных дисциплин

Протокол № __ от « __ » ______ 2007г.

Зав. кафедрой _______________Ан.И.Щербаков


Рекомендован для издания методической комиссией института

Протокол № ___ от «___ » ___________ 2007 г.

Секретарь комиссии _________О.Ю. Сиялко


Утверждаю

Проректор по учебной работе

_____________ Г.А. Мартынов

«____» _____________ 2007 г.


Зарегистрирован в методкабинете «_____» ________________ 2007г.

Регистрационный номер _______

СОДЕРЖАНИЕ

Введение 4

1 Учебно-тематические планы 5

1.1 Учебно-тематический план занятий

для студентов очной формы обучения 5

1.2 Учебно-тематический план занятий

для студентов заочной формы обучения 7

2 Учебная программа дисциплины 9

3 Список литературы 11

4 Планы практических занятий

для студентов очной формы обучения 12

5 Планы практических занятий

для студентов заочной формы обучения 16

6 Методические рекомендации по выбору и выполнению

контрольной работы для студентов заочной формы обучения 17

7 Задания для контрольной работы 18

8 Контрольные вопросы для самостоятельной проверки знаний 23

9 Примерные вопросы зачету 24


ВВЕДЕНИЕ


Предметом учебной дисциплины «Экономико-математические методы» является математический анализ общественных явлений, а также количественное выражение закономерностей общественного развития в конкретных условиях места и времени.

Экономико-математические методы дают количественную и качественную характеристику изучаемых процессов и закономерностей, позволяют раскрывать взаимосвязь между явлениями и процессами, находить оптимальные управленческие решения.

Цель преподавания дисциплины заключается в подготовке специалистов, умеющих проводить экономический анализ состояния и развития общественного производства, а также находить наиболее оптимальные пути повышения его эффективности, используя математические методы. Этой цели соответствуют содержание и структура курса, а также стоящие перед ним задачи.


В результате изучения дисциплины студенты должны:

- знать основные математические модели и методы исследования для различных сфер экономики.

- уметь применять модели и методы математики для анализа экономических систем, делать обоснованные выводы о развитии экономических процессов и явлений.

1. УЧЕБНО-ТЕМАТИЧЕСКИЕ ПЛАНЫ ЗАНЯТИЙ
   

1. УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН ЗАНЯТИЙ
   

для студентов очной формы обучения

№ п/п	Наименование темы	Количество часов
		Аудиторные занятия				Сам. работа	Всего
		Специальность	всего ауд.	лек-ции	практ.занят.
3 семестр
1	Экономико-математические методы и модели	ФиК АУ ЭиУп	2 2 2	2 2 2	- - -	4 4 2	4 6 4
2	Математическое программирование, его место при принятии управленческих решений	ФиК АУ ЭиУп	10 10 10	6 6 6	4 4 4	12 10 10	22 20 20
3	Экономическая динамика. Примеры моделей	ФиК АУ ЭиУп	2 2 2	2 2 2	- - -	4 2 2	4 4 4
4	Математические модели оптимальных процессов управления	ФиК АУ ЭиУп	2 2 2	2 2 2	- - -	4 2 2	4 4 4
5	Дискретные процессы. Динамическое программирование	ФиК АУ ЭиУп	4 4 4	2 2 2	2 2 2	4 4 2	8 8 6
6	Задача оптимального управления для непрерывных процессов	ФиК АУ ЭиУп	2 2 2	2 2 2	- - -	2 2 2	4 4 4
7	Метод вариационного исчисления и его применение	ФиК АУ ЭиУп	4 4 4	2 2 2	2 2 2	4 4 2	12 8 6
8	Методы статистического моделирования и их применение в экономике	ФиК АУ ЭиУп	4 4 4	2 2 2	2 2 2	4 4 2	10 8 6
9	Математические методы принятия решений в условиях неопределенности и риска	ФиК АУ ЭиУп	4 4 4	2 2 2	2 2 2	6 4 2	8 8 6
10	Принятие решений в условиях конфликта (элементы теории игр)	ФиК АУ ЭиУп	4 4 4	3 3 3	1 1 1	4 2 2	8 6 6
11	Теория графов. Сетевые модели	ФиК АУ ЭиУп	4 4 4	3 3 3	1 1 1	2 2 2	6 6 6
12	Методы и модели массового обслуживания	ФиК АУ ЭиУп	2 2 2	2 2 2	- - -	2 2 2	4 4 4
13	Многокритериальная оптимизация	ФиК АУ ЭиУп	2 2 2	2 2 2	- - -	2 2 2	4 4 4
Всего:		ФиК АУ ЭиУп	46 46 46	32 32 32	14 14 14	54 44 34	100 90 80
Форма итогового контроля:		Зачет

2. УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН ЗАНЯТИЙ
   

для студентов заочной формы обучения

№ п/п	Наименование темы	Количество часов
		Аудиторные занятия				Сам. работа	Всего
		Специальность	всего ауд.	лек-ции	практ.занят.
2 семестр (ВПО, СПО) 4 семестр (СОО)
1	Экономико-математические методы и модели	ФиК АУ ЭиУп	- - -	- - -	- - -	4 4 4	4 4 4
2	Математическое программирование, его место при принятии управленческих решений	ФиК АУ ЭиУп	4 4 4	2 2 2	2 2 2	14 12 10	18 16 14
3	Экономическая динамика. Примеры моделей	ФиК АУ ЭиУп	- - -	- - -	- - -	6 6 4	6 6 4
4	Математические модели оптимальных процессов управления	ФиК АУ ЭиУп	1 1 1	1 1 1	- - -	8 6 6	9 7 7
5	Дискретные процессы. Динамическое программирование	ФиК АУ ЭиУп	- - -	- - -	- - -	6 6 6	6 6 6
6	Задача оптимального управления для непрерывных процессов	ФиК АУ ЭиУп	1 1 1	1 1 1	- - -	12 10 8	13 11 9
7	Метод вариационного исчисления и его применение	ФиК АУ ЭиУп	- - -	- - -	- - -	6 6 4	6 6 4
8	Методы статистического моделирования и их применение в экономике	ФиК АУ ЭиУп	1 1 1	1 1 1	- - -	6 6 6	7 7 7
9	Математические методы принятия решений в условиях неопределенности и риска	ФиК АУ ЭиУп	1 1 1	1 1 1	- - -	6 4 4	7 5 5
10	Принятие решений в условиях конфликта (элементы теории игр)	ФиК АУ ЭиУп	1 1 1	1 1 1	- - -	6 6 6	7 7 7
11	Теория графов. Сетевые модели	ФиК АУ ЭиУп	- - -	- - -	- - -	6 4 4	6 4 4
12	Методы и модели массового обслуживания	ФиК АУ ЭиУп	1 1 1	1 1 1	- - -	6 6 4	7 7 5
13	Многокритериальная оптимизация	ФиК АУ ЭиУп	- - -	- - -	- - -	4 4 4	4 4 4
Всего:		ФиК АУ ЭиУп	10 10 10	8 8 8	2 2 2	90 80 70	100 90 80
Форма итогового контроля:		Зачет, контрольная работа 3 семестр (ВПО, СПО) 5 семестр (СОО)

2 УЧЕБНАЯ ПРОГРАММА ДИСЦИПЛИНЫ


Тема 1. Экономико-математические методы и модели


Математические методы моделирования в экономике и их использование для выделения и формального описания наиболее важных связей экономических переменных. Обзор основных групп методов.


Тема 2. Математическое программирование, его место

при принятии управленческих решений


Задача и методы математического программирования. Задача линейного программирования. Задачи нелинейного программирования. Метод множителей Лагранжа. Численные методы оптимизации.


Тема 3. Экономическая динамика. Примеры моделей


Постановка задачи экономической динамики. Показатели экономической динамики. Понятие динамического равновесия. Модель макроэкономической динамики, модель Солоу, модель Харрода-Домара.


Тема 4. Математические модели оптимальных процессов

управления


Основные понятия теории оптимального управления. Постановка задачи оптимального управления. Критерии оптимальности. Методы нахождения оптимальных решений.


Тема 5. Дискретные процессы. Динамическое программирование


Оптимизация многошаговых процессов. Постановка задачи динамического программирования. Принцип оптимальности Р. Беллмана. Основное уравнение динамического программирования. Оптимизация дискретных и непрерывных систем.


Тема 6. Задача оптимального управления для непрерывных

процессов


Постановка основной задачи. Принцип максимума Понтрягина. Примеры применения принципа максимума. Задача синтеза оптимального управления.


Тема 7. Метод вариационного исчисления и его применение


Основные принципы вариационного исчисления. Каноническая форма уравнений Эйлера. Вариационные задача при наличии ограничений. Задачи с неподвижными границами. Достаточные условия экстремума. Вариационные задачи на условный экстремум. Принцип максимума и вариационное исчисление.


Тема 8. Методы статистического моделирования и их применение

в экономике


Методы получения случайных чисел с заданным законом распределения. Применение метода статистического моделирования к задачам оптимизации систем обслуживания, систем управления запасами и др.


Тема 9. Математические методы принятия решений в условиях

неопределенности и риска


Основные понятия теории принятия решений. Игры с «природой». Понятие риска и его оценка. Критерии оптимальности Вальда, Гурвица, Сэвиджа и др. Статистические решения и статистические решающие правила.


Тема 10. Принятие решений в условиях конфликта

(элементы теории игр)


Основные понятия теории игр и их классификация. Антагонистические игры. Седловая точка. Бескоалиционные игры. Ситуация равновесия.


Тема 11. Теория графов. Сетевые модели


Основные понятия теории графов. Виды графов. Классы задач, решаемых с помощью теории графов. Решение сетевых задач. Метод Крускаля. Метод Беллмана-Форда.


Тема 12. Методы и модели массового обслуживания


Системы массового обслуживания, их типы. Потоки событий. входящий и выходящий потоки. Вероятности состояний. Уравнения Колмогорова. Финальные вероятности. Оптимизация систем обслуживания.


Тема 13. Многокритериальная оптимизация


Постановка задачи многокритериальной оптимизации. Методы оптимизации: линейная свертка, метод контрольных показателей, введение метрики в пространстве критериев. Оптимальность по Парето.


3 СПИСОК ЛИТЕРАТУРЫ


Основная литература

1. Бурков, А. В. Моделирование экономических процессов и систем: учеб. пособие / А.В. Бурков, С.Л. Миньков, В.М. Ушаков. – Томск: Изд-во ТГПУ, 2001. – 158 с.
   
2. Замков, О. О. Математические методы в экономике / О.О. Замков, А.В. Толстопятенко, Ю.Н. Черемных.- М.: ДиС, 1997.
   
3. Математика в экономике: учебник. В 2 ч. Ч. 2 / Солодовников А. С. и др. – М.: Финансы и статистика, 1999. – 367 с.
   
4. Общий курс высшей математики: учебник / под ред. В. И. Ермакова. – М.: ИНФРА-М, 2002. – 656 с.
   

Дополнительная литература

5. Воробьев, Н. Н. Теория игр для экономистов – кибернетиков / Н.Н. Воробьев.- М.: Наука, 1985.
   
6. Дубров, А. М. Математико-статистическая оценка эффективности в экономических задачах / А.М. Дубров. – М.: Финансы и статистика, 1982. – 176 с.
   
7. Ермаков, С. М. Статистическое моделирование / С.М. Ермаков, Г.А. Михайлов.- М.: Наука, 1982.
   
8. Кузнецов, А. В. Высшая математика. Математическое программирование: учебник /А. В. Кузнецов, В. А. Сакович, Н. И. Холод. – Мн.: Выш. шк., 1994. – 286 с.
   
9. Мышкис, А. Д. Элементы теории математических моделей / А.Д. Мышкис. – М.: Физматгиз, 1994. – 192 с.
   
10. Раскин, Л. Г. Анализ сложных систем и элементы теории оптимального управления / Л.Г. Раскин. – М., 1976. – 344 с.
    
11. Справочник по математике для экономистов / под ред. В. И. Ермакова. – М.: В. шк., 1997. – 384 с.
    
12. Таха, Х. Введение в исследование операций. В 2 кн / Х. Таха. - М.: Мир, 1985.
    
13. Теория массового обслуживания / Г.И. Ивченко и др.- М.: Высш. школа, 1982.
    
14. Теория прогнозирования и принятия решений / С.А. Саркисян и др.- М.: Высш. школа, 1977.
    

4 ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

для студентов очной формы обучения


Тема 1. Математическое программирование,

его место при принятии управленческих решений

Время - 4 часа


Задача нелинейного программирования без ограничений. Необходимые и достаточные условия экстремума. Задача нелинейного программирования с ограничениями. Метод множителей Лагранжа. Необходимое условие экстремума. Выпуклые функции, достаточные условия экстремума.


Типовое задание. Решить задачу потребительского выбора: найти функции спроса при доходе I = 60 и ценах благ p₁ = 10 и p₂ = 2 со следующими функциями предпочтения:


1) u = x₁ x₂ → max; 2) u = x₁^1/3 x₂^2/3 → max;

3) u = (x₁ -1)^1/4( x₂ -3)^3/4 → max; 4) u = 5(4- x₁)² +(20 - x₂)² → min.


Литература: [4,8]


Тема 2. Дискретные процессы. Динамическое программирование

Время - 2 часа


Постановка задачи динамического программирования. Уравнение Беллмана. Метод решения уравнения Беллмана.


Типовое задание 1. Методом динамического программирования для заданной сетевой модели определить оптимальный путь из пункта А в пункт В:

а) с наименьшей стоимостью; б) с наибольшей стоимостью.


Типовое задание 2. Решить задачу распределения капиталовложений при следующих условиях. Пусть фирма имеет несколько предприятий. Для их расширения выделяются средства в объеме N единиц. Каждое предприятие представляет на рассмотрение проекты, которые характеризуются величинами суммарных затрат (С ед.) и доходов (R ед.), связанных с их реализацией (см. исходные данные в табл.).

№ проекта	Предприятие 1		Предприятие 2		Предприятие 3
	C1	R1	C2	R2	C3	R3
1 2 3 4	3 4 - -	5 6 - -	3 4 5 -	4 5 8 -	0 2 3 6	0 3 5 4

Построить сетевую модель динамического программирования с целью максимизации дохода фирмы при N =8.


Литература: [1,8]


Тема 3. Метод вариационного исчисления и его применение

Время - 2 часа


Постановка задачи вариационного исчисления. Уравнение Эйлера. Задача синтеза оптимального управления.


Типовое задание. Найти путь у = у(х) наименьшей стоимости, выводящий экономическую систему из состояния А(х₁, у₁) в планируемое состояние В(х₂, у₂), если эффективность системы определяется функционалом:

а)

б) .

Воспользоваться необходимым условием вариационного исчисления – уравнением Эйлера. Найти явный вид функции у = у(х) и функционала стоимости L(y(x)).


Литература: [1]


Тема 4. Методы статистического моделирования и

их применение в экономике

Время - 2 часа


Методы получения случайных чисел с заданным законом распределения. Применение метода статистического моделирования к задачам оптимизации систем обслуживания, систем управления запасами и др.


Типовое задание. Методом обратной функции получить формулу для моделирования значений следующих непрерывных распределений:

а) экспоненциальное распределение с плотностью ;

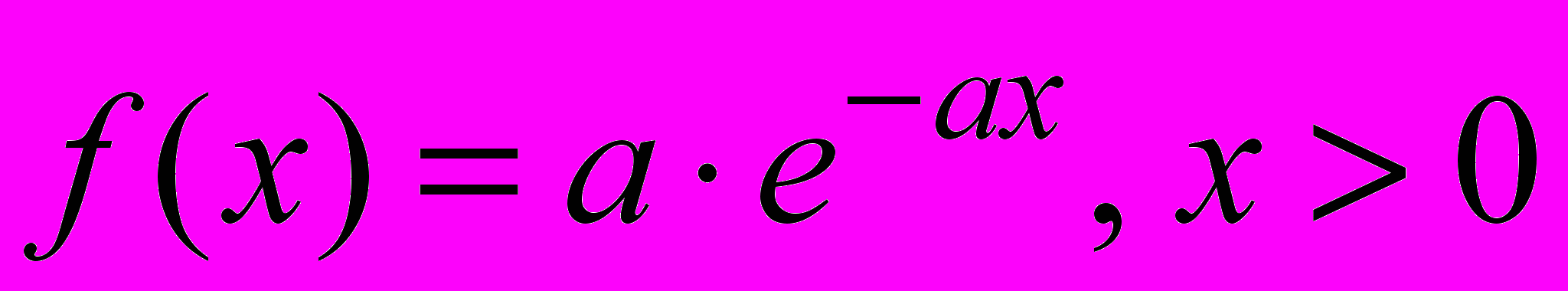б) распределение Релея с плотностью .

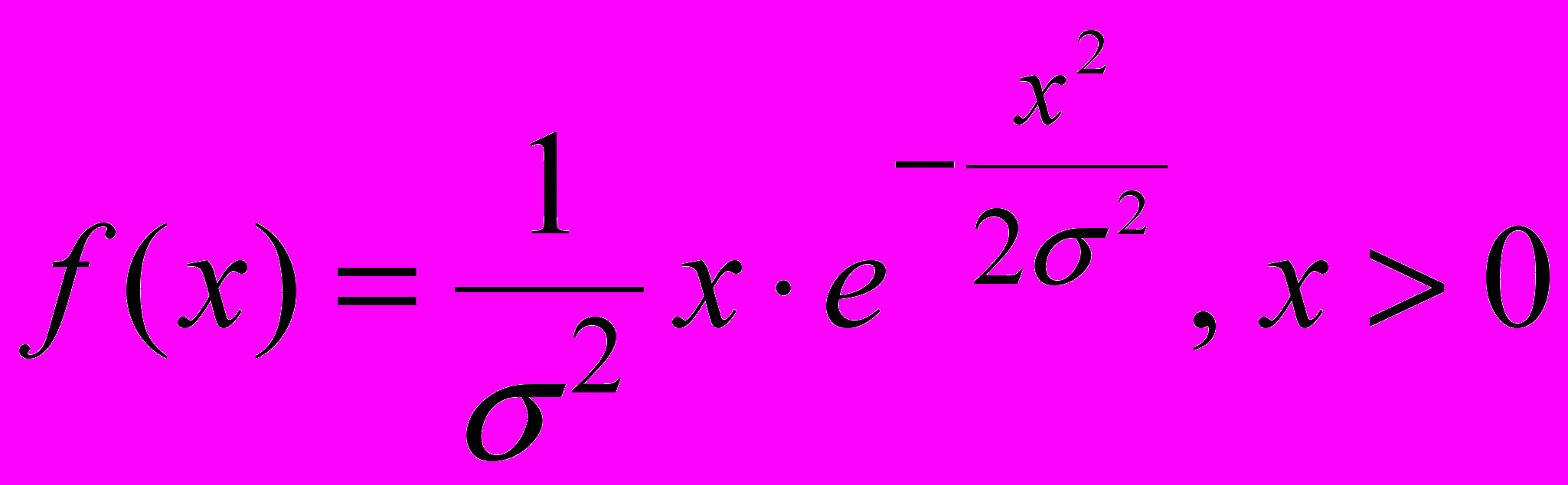С помощью найденных формул получить по 10 реализаций значений заданных случайных величин.


Литература: [1,2]


Тема 5. Математические методы принятия решений в условиях

неопределенности и риска

Время - 2 часа


Игры с «природой». Критерии оптимальности: Гурвица, Севиджа, минимакса. Статистические решение и статистические решающие правила.

Типовое задание. Рассмотрим игру с природой, заданную следующей матрицей:

	S1	S2	S3	S4
α1	20	30	15	15
α2	75	20	35	20
α3	25	80	25	25
α4	85	5	45	5

где числа задают выигрыши игрока в различных ситуациях, определяемых состоянием «природы» S и выбором игрока α. Найти оптимальные стратегии игрока по критериям: Вальда, Сэвиджа, Байеса, Гурвица.


Литература: [2]


Тема 6. Принятие решений в условиях конфликта

(элементы теории игр). Теория графов. Сетевые модели

Время - 2 часа


Нахождение седловых точек и ситуаций равновесия в антагонистических и бескоалиционных играх. Определение решения в кооперативных играх.


Типовое задание 1. Рассматривается экономика, в которой имеется два субъекта: Игрок 1 и Игрок 2. Игроки выбирают стратегии (принимают решения) независимо друг от друга; соглашения не допускаются. Функции выигрыша игроков Н₁ и Н₂ в зависимости от их стратегий х₁ и х₂ заданы в виде матриц:

Н1(х1, х2) =		х1	х2	Н2(х1, х2) =		х1	х2
	х1	4	0		х1	1	0
	х2	2	1		х2	2	4

Найти ситуации равновесия для игроков и их оптимальные выигрыши.


Виды графов. Решение сетевых задач. Метод Крускаля. Метод Беллмана-Форда.

Типовое задание 2. Построить остовное дерево минимального веса (МОД) для заданного неориентированного графа методом Крускаля.

Типовое задание 3. Для заданного ориентированного графа определить кратчайший маршрут методом Беллмана-Форда.


Литература: [2, 4, 8].


5 ПЛАНЫ ПРАКТИЧЕСКИХ ЗАНЯТИЙ

для студентов заочной формы обучения


Тема 1. Математическое программирование,

его место при принятии управленческих решений

Время - 2 часа


Задача нелинейного программирования без ограничений. Необходимые и достаточные условия экстремума. Задача нелинейного программирования с ограничениями. Метод множителей Лагранжа. Необходимое условие экстремума. Выпуклые функции, достаточные условия экстремума.


Типовое задание. Решить задачу потребительского выбора: найти функции спроса при доходе I = 60 и ценах благ p₁ = 10 и p₂ = 2 со следующими функциями предпочтения:


1) u = x₁ x₂ → max; 2) u = x₁^1/3 x₂^2/3 → max;

3) u = (x₁ -1)^1/4( x₂ -3)^3/4 → max; 4) u = 5(4- x₁)² +(20 - x₂)² → min.


Литература: [4,8]


6 МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ВЫБОРУ И ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

для студентов заочной формы обучения


Контрольная работа по дисциплине представлена 3 вариантами, каждый из которых содержит три задачи:

- задача 1 относится к теме «Нелинейное программирование» и предполагает знание необходимого условия экстремума и умение им пользоваться для нахождения минимума функции потерь и определения оптимального объема поставки;

- задача 2 относится к теме «Динамическое программирование» и предполагает знание метода динамического программирования и умение им пользоваться для определения оптимальных маршрутов по сетям;

- задача 3 относится к теме «Стохастическое программирование» и включает задачи на изучение случайного спроса, его прогнозирование, а также на оптимизацию систем обслуживания.

Выбор варианта контрольной работы осуществляется по последней цифре номера зачетной книжки:

№ варианта	Последняя цифра номера зачетной книжки
1	1, 2, 3
2	4, 5, 6
3	7, 8, 9, 0

При выполнении контрольной работы необходимо пользоваться материалами лекций и практических занятий, а также учебной литературой, примерный список которой приведен в разделе 3 УМКд.

В каждой задаче нужно приводить условие и исходные данные. В решении должны быть представлены формулы, а также последовательность действий по их применению (т. е. недостаточно после формул сразу писать ответы).

Контрольная работа должна быть оформлена в соответствии с имеющимися требованиями в тетради или на отдельных листах формата А4 (в переплетенном виде, например, в скоросшивателе) и может быть написана от руки либо напечатана.


7 ЗАДАНИЯ ДЛЯ КОНТРОЛЬНОЙ РАБОТЫ

Вариант 1

Задача 1. Задача оптимальной поставки продукции

Пусть задан вид функции потерь, которые имеют место в задаче определении объема поставки:



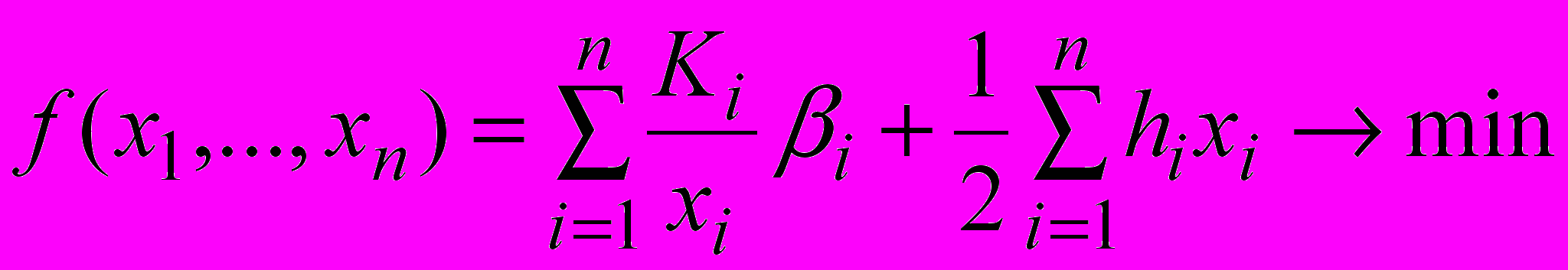
где

х_i – объем поставки продукции i-го вида (i = 1,…, n);

К_i – стоимость поставки объема х_i продукции i-го вида;

β_i – спрос (количество единиц продукции i-го вида, запрашиваемых в единицу времени);

h_i – затраты на хранение единицы продукции i-го вида в единицу времени.


Требуется:

1. получить аналитическое выражение для нахождения значений х_i, доставляющих минимум функции потерь в единицу времени;
   
2. определить оптимальный объем поставки и величину потерь при заданных значениях параметров задачи:
   

n = 2; К₁= 100; К₂ = 150; β₁ = 10; β₂ = 30; h₁ = 1; h₂ = 3.


Задача 2. Задача оптимизации маршрута

Динамический процесс изменения состояний некоторой системы во времени представлен в виде ориентированного графа:




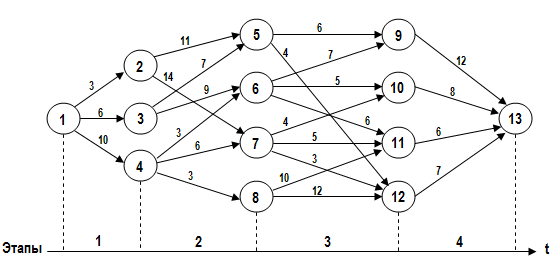
где i, j – номера состояний системы (в кружочках); числа а_ij – стоимости переходов из состояния i в состояние j; стрелками обозначены возможные переходы из состояния в состояние (т. е. возможные управления).


Применяя метод динамического программирования, найти оптимальный маршрут из состояния 1 в состояние 13 и его оценку с точки зрения:

а) минимальной стоимости маршрута;

б) максимальной стоимости маршрута.


Задача 3. Оптимальное управление объемом поставок при случайном спросе

Пусть для задачи оптимизации объемов поставок при случайном спросе функция потерь имеет вид:




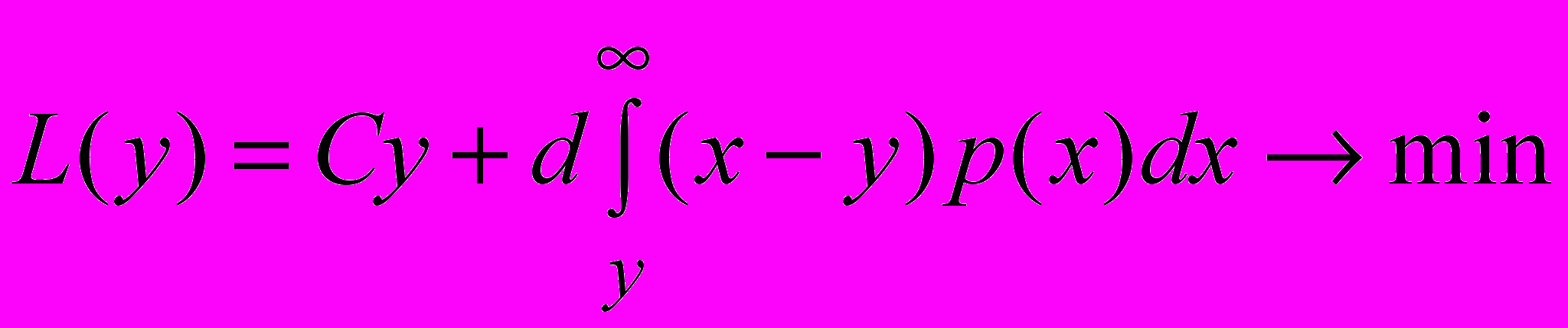
где

у – объем поставки в начале периода;

х – величина спроса (случайная величина с плотностью р(х));

С – издержки на единицу продукции, связанные с поставкой;

d – издержки на единицу продукции из-за отсутствия в продаже (дефицит).


Определить оптимальный объем поставки у, если плотность распределения спроса задана в виде:



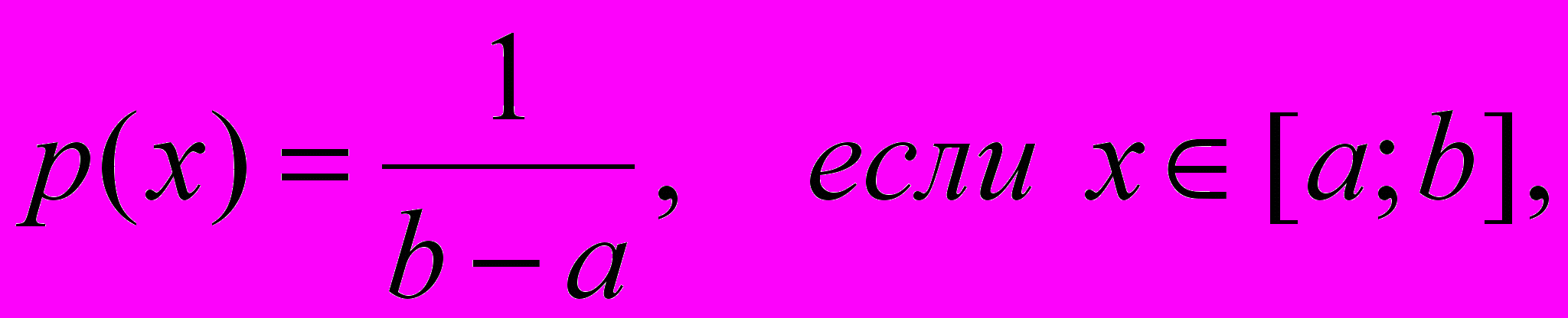
где а, b – минимальное и максимальное значения величины спроса.

Вариант 2

Задача 1. Задача потребительского выбора

Пусть функция полезности задана в виде:



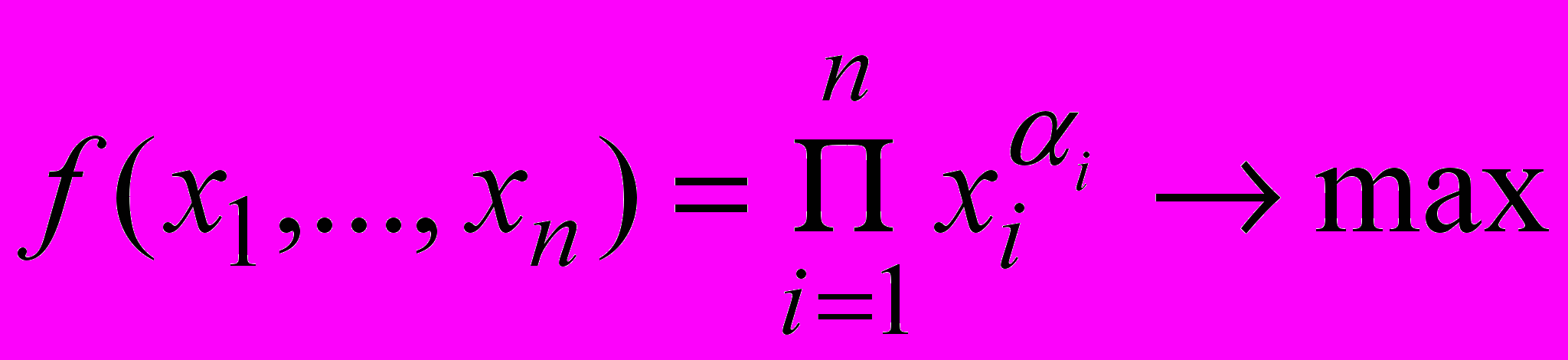
при ограничении


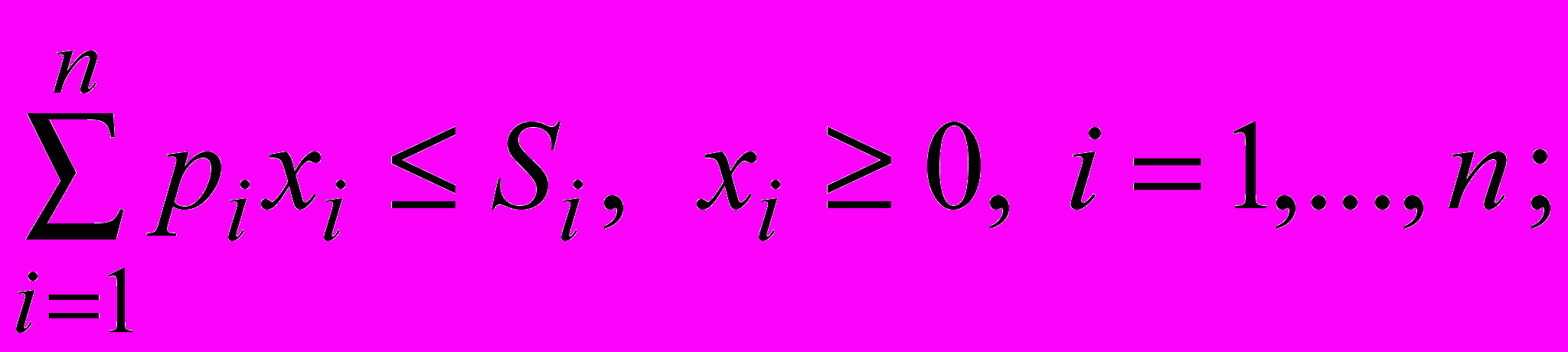
где



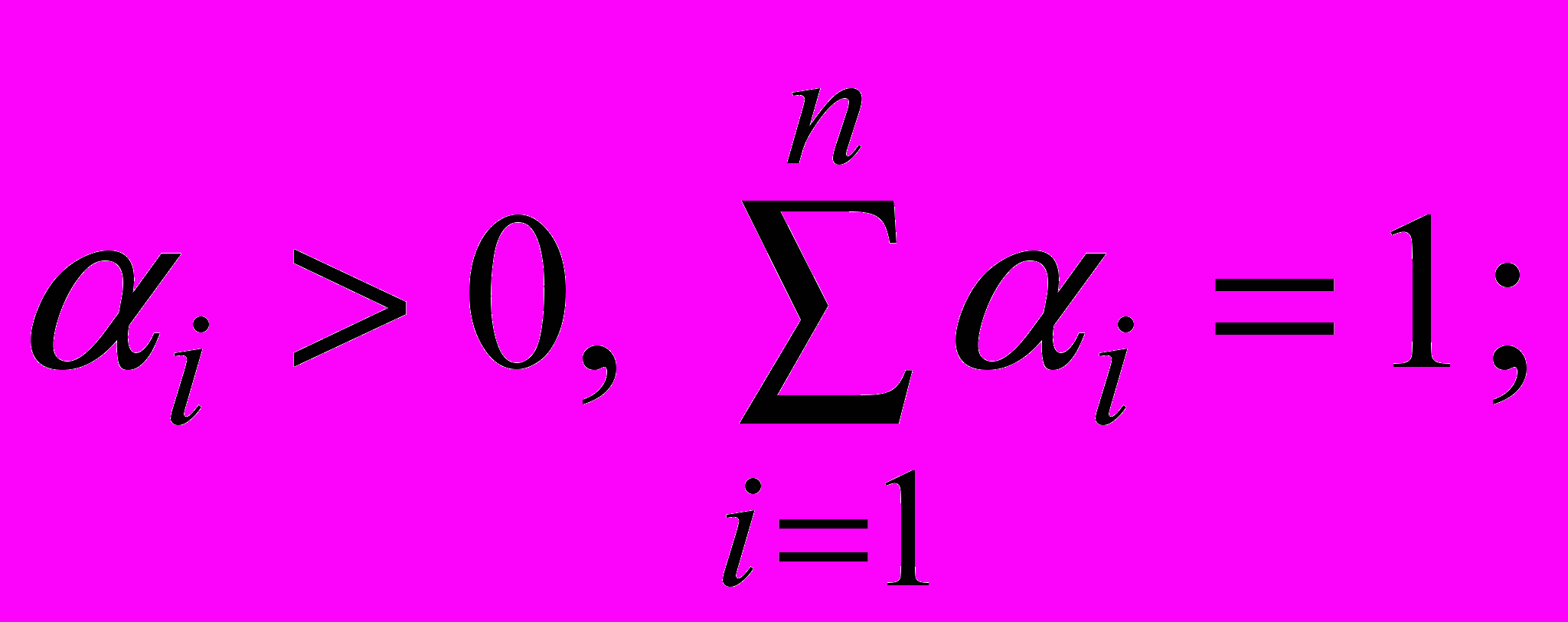
х_i – количество единиц i-го блага;

р_i – стоимость единицы i-го блага;

S – бюджетное ограничение.


Требуется:

1. получить аналитическое выражение для нахождения значений х_i, доставляющих максимум функции полезности в единицу времени;
   
2. определить оптимальный объем поставки и величину потерь при заданных значениях параметров задачи:
   

n = 2; 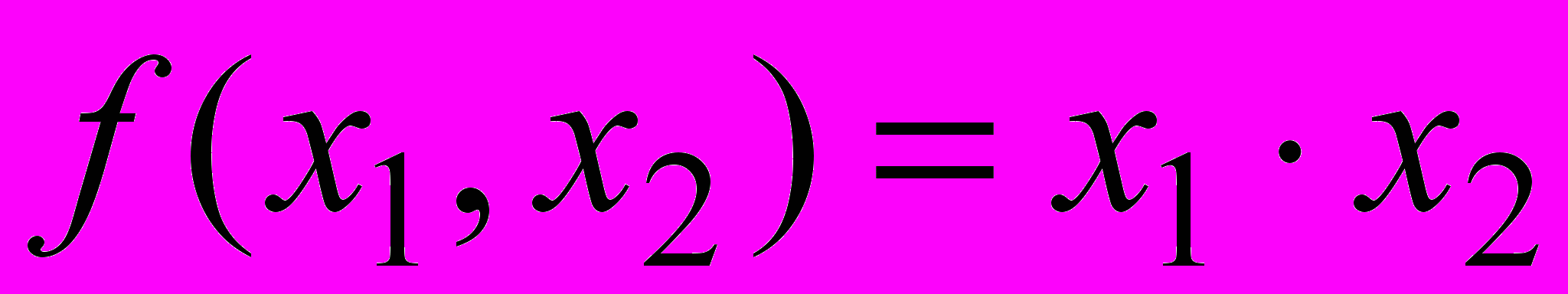; p₁ = 10; p₂ = 2; S = 60.


Предложить метод решения для нахождения значений х, доставляющих максимум функции полезности.


Задача 2. Задача оптимизации маршрута

Динамический процесс изменения состояний некоторой системы во времени представлен в виде ориентированного графа:



где i, j – номера состояний системы (в кружочках); числа а_ij – стоимости переходов из состояния i в состояние j; стрелками обозначены возможные переходы из состояния в состояние (т. е. возможные управления).


Применяя метод динамического программирования, найти оптимальный маршрут из состояния 1 в состояние 13 и его оценку с точки зрения:

а) минимальной стоимости маршрута;

б) максимальной стоимости маршрута.


Задача 3. Задача оптимального управления объемом поставок при случайном спросе

Пусть для задачи оптимизации объемов поставок при случайном спросе функция потерь имеет вид:



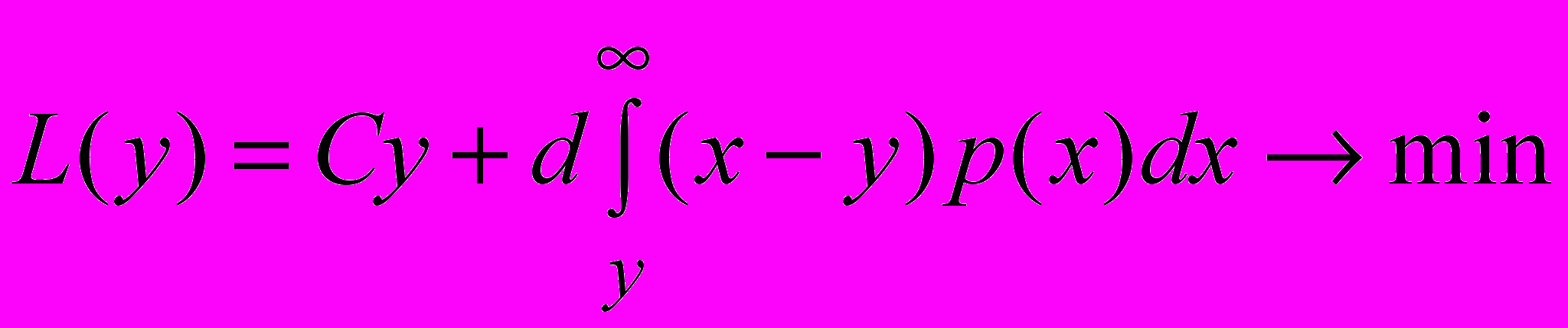
где

у – объем поставки в начале периода;

х – величина спроса (случайная величина с плотностью р(х));

С – издержки на единицу продукции, связанные с поставкой;

d – издержки на единицу продукции из-за отсутствия в продаже (дефицит).

Определить оптимальный объем поставки у, если плотность распределения спроса задана в виде:

,

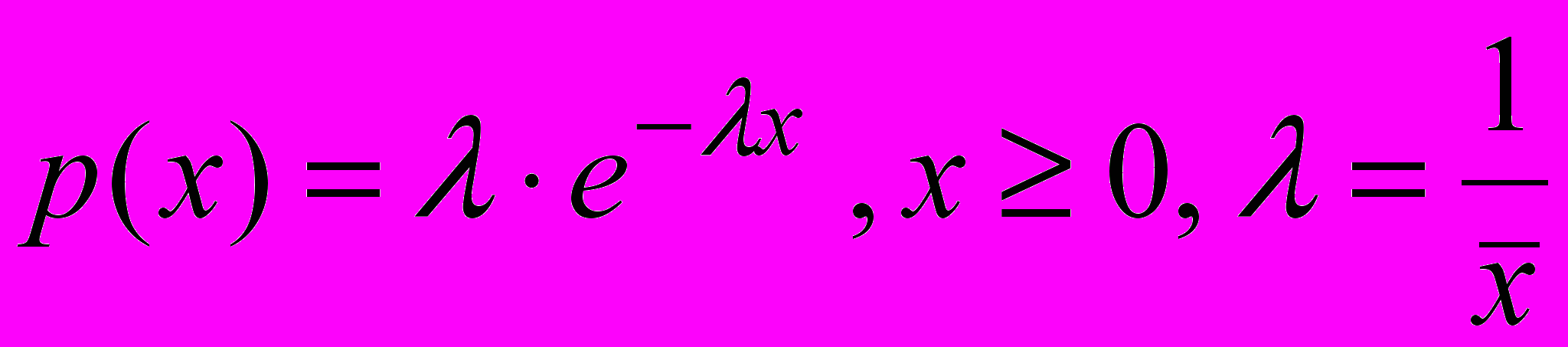где 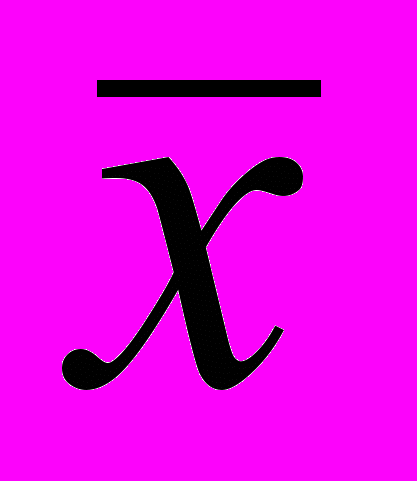– средняя величина спроса.

Вариант 3

Задача 1. Задача определения оптимальных объемов производства

Пусть функция дохода задана в виде:




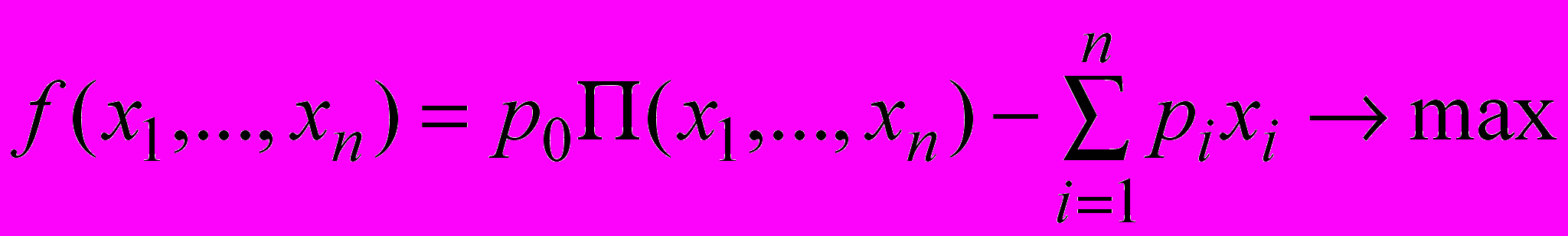
где

х_i – количество ресурсов i-го вида;

р_i – стоимость единицы ресурса i-го вида;

р₀ – рыночная цена единицы произведенной продукции;

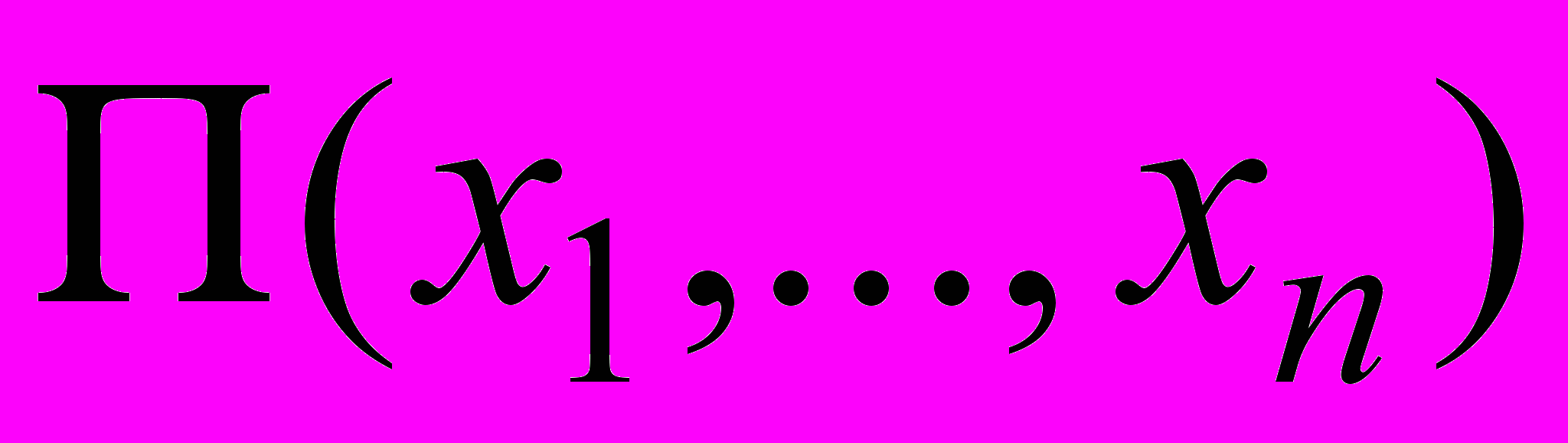– производственная функция (количество продукции, получаемой из ресурсов ).


Требуется:

1. получить аналитическое выражение для нахождения значений х_i, доставляющих максимум функции дохода;
   
2. определить оптимальные объемы производства и величину дохода при заданных значениях параметров задачи:
   

n = 2; 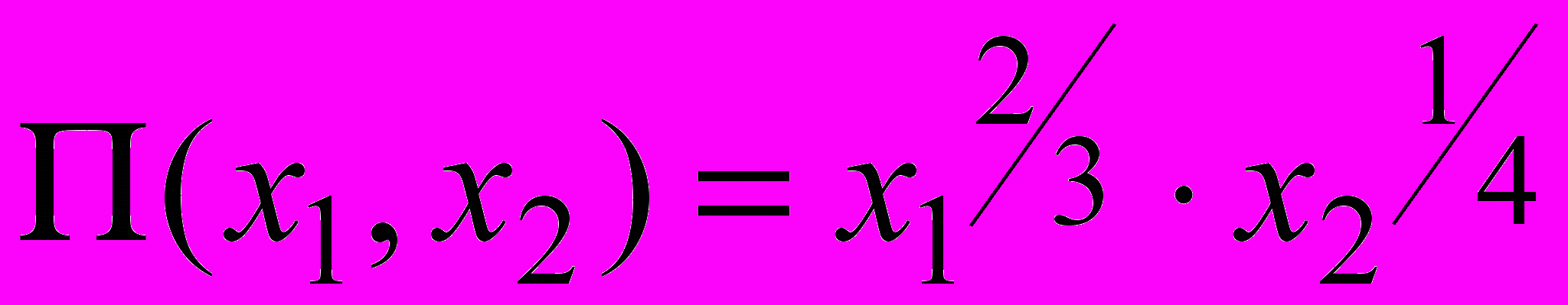; p₁ = 50; p₂ = 100; p₀ = 140.


Задача 2. Задача оптимизации маршрута

Динамический процесс изменения состояний некоторой системы во времени представлен в виде ориентированного графа:



где i, j – номера состояний системы (в кружочках); числа а_ij – стоимости переходов из состояния i в состояние j; стрелками обозначены возможные переходы из состояния в состояние (т. е. возможные управления).


Применяя метод динамического программирования, найти оптимальный маршрут из состояния 1 в состояние 13 и его оценку с точки зрения:

а) минимальной стоимости маршрута;

б) максимальной стоимости маршрута.


Задача 3. Задача оптимального управления объемом поставок при случайном спросе

Пусть для задачи оптимизации объемов поставок при случайном спросе функция потерь имеет вид:



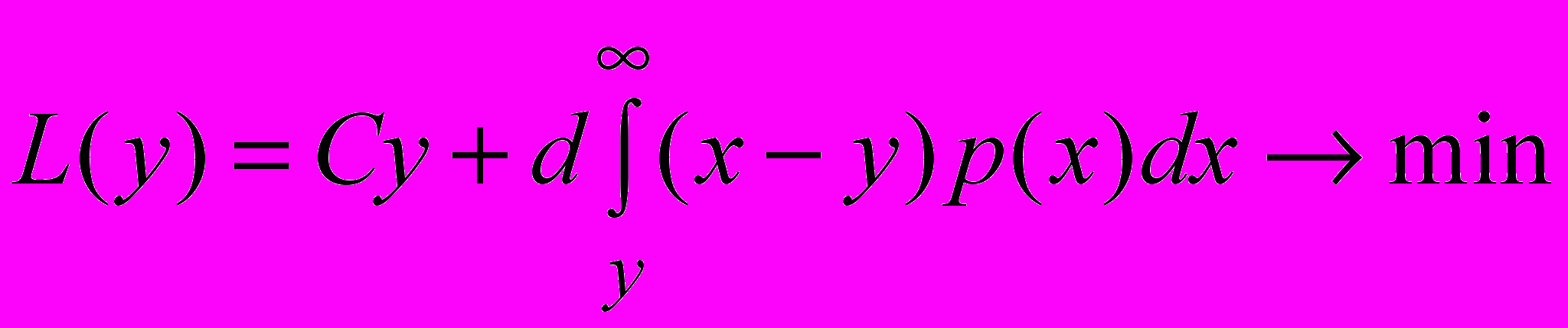
где

у – объем поставки в начале периода;

х – величина спроса (случайная величина с плотностью р(х));

С – издержки на единицу продукции, связанные с поставкой;

d – издержки на единицу продукции из-за отсутствия в продаже (дефицит).


Определить оптимальный объем поставки у, если плотность распределения спроса задана в виде:

.


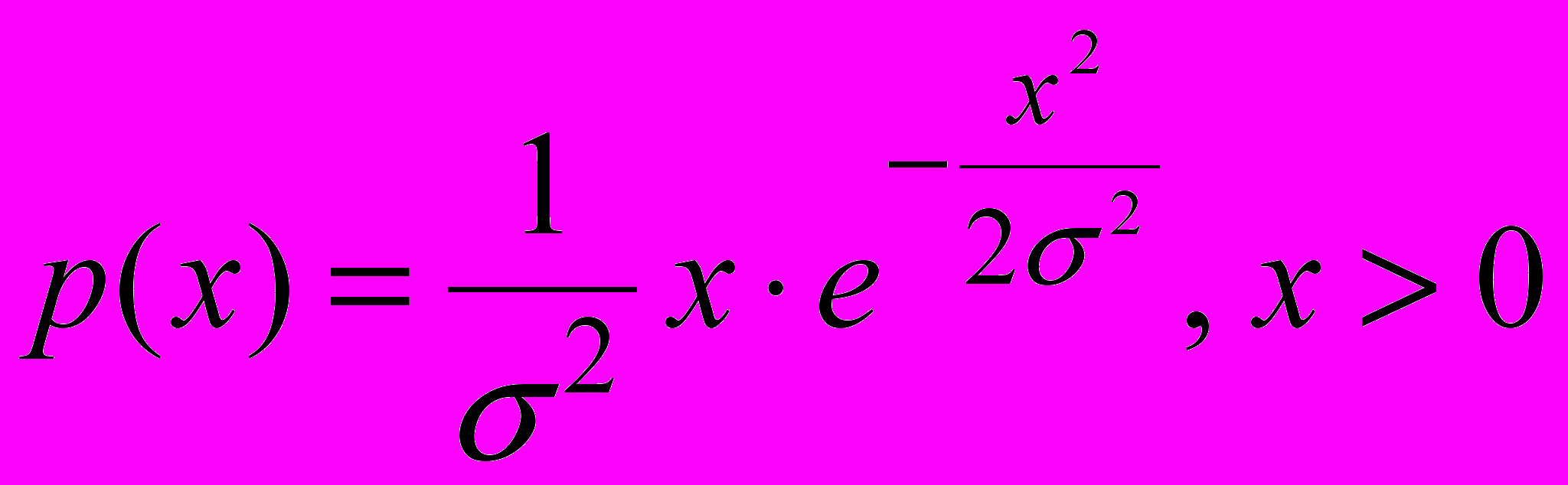8 КОНТРОЛЬНЫЕ ВОПРОСЫ

для самостоятельной проверки знаний

1. Какие основные группы математических методов применяются в экономике?
   
2. Какие основные задачи решаются методами математического программирования?
   
3. Какие бывают виды задач нелинейного программирования?
   
4. В чём состоит задача линейного программирования?
   
5. В чём суть теории двойственности задач ЛП?
   
6. Какие классы задач формализуются моделью задачи ЛП?
   
7. В чём состоит основная задача экономической динамики?
   
8. Какие показатели используются при оценке экономической динамики?
   
9. Что означает термин «динамическое равновесие»?
   
10. Какие вы знаете модели макроэкономической динамики?
    
11. В чем состоит задача оптимального управления динамическими процессами в экономике?
    
12. В чем состоит принцип оптимальности Р. Беллмана?
    
13. В каких задачах используется принцип максимума Понтрягина?
    
14. Какие задачи решаются методами вариационного исчисления?
    
15. чем суть метода статистического моделирования?
    
16. На чём основаны моделирование и оптимизация сложных систем?
    
17. Что является математической моделью конфликтной ситуации?
    
18. Какими методами анализируются конфликтные ситуации в экономике?
    
19. Какая игра называется антагонистической?
    
20. В чём состоит принцип минимакса?
    
21. Что подразумевает понятие игры с непротивоположными интересами?
    
22. Что такое игры с «природой»?
    
23. Какие вы знаете критерии принятия решений?
    
24. Как оцениваются риски с помощью количественных методов?
    
25. Что является предметом изучения в теории графов?
    
26. Какие вы знаете виды графов?
    
27. Что означает термин «сетевое управление»?
    
28. Из каких основных элементов состоит система массового обслуживания?
    
29. Что подразумевает термин «финальные вероятности состояний»?
    
30. Какие основные методы применяются для решения многокритериальных задач оптимизации?
    

9 ПРИМЕРНЫЕ ВОПРОСЫ К ЗАЧЕТУ

1. Задача нелинейного программирования без ограничений. Примеры.
   
2. Задача нелинейного программирования с ограничениями.
   
3. Метод множителей Лагранжа.
   
4. Численные методы решения задач нелинейного программирования.
   
5. Основные показатели динамики, их содержательный смысл.
   
6. Равновесие в динамических системах.
   
7. Модель макроэкономической динамики Солоу.
   
8. Модель макроэкономической динамики Харрода-Домара.
   
9. Общая постановка задачи теории оптимального управления. Критерии оптимальности.
   
10. Постановка задачи динамического программирования.
    
11. Принцип оптимальности Р. Беллмана. Основное уравнение динамического программирования.
    
12. Принцип максимума Понтрягина для непрерывных процессов.
    
13. Задача синтеза оптимального управления.
    
14. Основные принципы вариационного исчисления.
    
15. Каноническая форма уравнений Эйлера.
    
16. Достаточные условия экстремума в вариационных задачах.
    
17. Постановка вариационной задачи на условный экстремум.
    
18. Статистическое моделирование. Методы получения случайных чисел
    
19. Методы статистического моделирования.
    
20. Задачи принятия решения в условиях риска. Критерии оптимальности.
    
21. Задачи принятия решения в условиях неопределенности. Критерии оптимальности.
    
22. Модель антагонистического конфликта. Седловая точка.
    
23. Модель неантагонистического конфликта. Ситуация равновесия.
    
24. Кооперация. Модель. Дележи.
    
25. Многокритериальные задачи. Оптимальность по Парето.
    

Оригинал-макет учебно-методического комплекса дисциплины

НОУ ВПО КузИЭП


Подписано в печать АКТ № « » 200 г.


Формат 60 х 90/16

Объем - п.л. Тираж экз.


Стоимость руб.


Бумага многофункциональная офисная

Отпечатано в копировально-множительном отделе

Кузбасского института экономики и права