Geum.ru

Дополнительные образовательные программы. Повышение квалификации Кострома, 2000 Сборник печатается по решению Ученого Совета Костромского института повышения квалификации

Вид материалаДокументы
Ректор Костромского областного
Категория слушателей
Режим занятий
Наименование разделов и дисциплин
Наименование разделов, дисциплин и тем
Содержание занятий
Тема 2. Развитие понятия число, числа и выражения.
Тема 3. Тождественные преобразования в курсе алгебры.
Тема 4. Основы математического анализа.
Тема 5. Формирование геометрических знаний, умений.
Тема 6. Тригонометрический круг и числовая прямая в решении задач по тригонометрии.
Тема 7. Урок математики в современной школе.
Тема 8. Анализ результатов экзаменов.
Тема 9. Внеклассная работа по математике.
Тема 11. Итоговый контроль.
Подобный материал:
1   ...   4   5   6   7   8   9   10   11   ...   43

Ректор Костромского областного


института повышения квалификации

работников образования

_____________________ Лушина Е.А.



Образовательная программа курса

«Теория и методика преподавания математики»


Цель: создание условий для углубления теоретической предметной подготовки обновления знаний по методике преподавания предмета.

Категория слушателей: учителя математики основной и старшей школы.

Срок обучения: 156 часов + 12 = 168

Формы обучения: с отрывом от работы, с частичным отрывом от работы.

Режим занятий: 6 ч. (36 ч. в нед.); 4 ч. (24 ч. в нед.).


Учебный план



№
Наименование разделов и дисциплин
Всего часов
В том числе
Форма контроля

Лекции
Практические занятия

I
Цель, структура, содержание базового математического образования.
8
6
2
Собеседование

II
Цель, содержание, методика обучения учащихся вопросам арифметики.
18
10
8
Аукцион

III
Цель, содержание, методика обучения учащихся алгебре.
28
16
12
Контрольная работа

IV
Цель, содержание, методика обучения учащихся алгебре и началом анализа.
18
8
10
Зачет

V
Цель. Содержание, методика обучения учащихся геометрии.
32
22
10
Зачет

VI
Цель, содержание, методика обучения учащихся вопросам тригонометрии.
14
6
8
Семинар

YII
Технологии обучения учащихся математике
16
12
4



YШ
Формы, методы, средства контроля за уровнем математической подготовки школьников
14
4
10
Зачет

IX
Внеклассная работа по математике
8
6
2
Круглый стол

X
Спецкурсы









Реферат

XI
Итоговый контроль
12



12






Итого
168
90
78




Учебно-тематический план


№
Наименование разделов, дисциплин и тем
Всего часов
В том числе
Форма контроля

Лекции
Выездные занятия, стажировка, деловые игры и др.
Практические, лабораторные, семинары

I
Цели, структура, содержание базового математического образования
8
6



2
Собеседование

1.1
Концепция школьного математического образования
2
2









1.2
Обязательные результаты обучения математике
2
2









1.3
Структурные, методические и содержательные особенности основных и параллельных учебников
2
2









1.4
Роль математического образования в формировании личности
2



2






II
Цели, содержание, методика обучения учащихся вопросам арифметики
18
10
2
6
Аукцион

2.1
Содержательные линии курса арифметики















2.2
Методика формирования понятия числа.
2
2









2.3
Основы арифметики 5 – 6 классы. Методика изучения основ арифметики
4
2



2



2.4
Проценты. Методика решения задач на проценты
4
2



2



2.5
Методика решения текстовых задач арифметическим способом
4
2



2



2.6
Приемы устной работы на уроках математики. Отработка приемов устных вычислений
2
2









2.7
Приемственность в обучении математике
2



2






III
Цели. Содержание, методика обучения учащихся алгебре
28
16



12
Контрольная работа

3.1
Содержательные линии курса алгебры и их теоретическое и методическое обоснование
2
2









3.2
Тождественные преобразования выражений
6
4



2



3.3
Уравнения и неравенства. Системы
4
2



2



3.4
Уравнения и неравенства с параметрами
4
2



2



3.5
Модуль в алгебре
4
2



2



3.6
Функции и их графики. Свойства
4
2



2



3.7
Методика обучения учащихся решению задач с помощью уравнения и системы уравнений
4
2



2



IV
Цели. Содержание. Методика обучения учащихся алгебре и началам анализа
18
8
2
8
Зачет

4.1
Содержание курса алгебры и начала анализа 10 – 11 классах. Программа. Учебники
4
2



2



4.2
Теория пределов. Непрерывность. Производная. Техника дифференцирования. Применение производной
6
2
2
2



4.3
Первообразная. Интеграл. Применение первообразной в решении технических задач
4
2



2



4.4
Показательная, логарифмическая, степенная функции и их производные
4
2



2



V
Цели. Содержание, методика обучения учащихся геометрии
32
22
4
6
Зачет

5.1
Программа. Теоретические, методические, структурные особенности учебников геометрии

2
2









5.2
Аксиоматическое и логическое построение курса геометрии А.В. Погорелова
4
2
2






5.3
Основные геометрические фигуры и их свойства. Формирование геометрических знаний и умений
4
2



2



5.4
Параллельность в плоскости и пространстве
2
2









5.5
Перпендикулярность в плоскости и пространстве
2
2









5.6
Геометрические преобразования на плоскости и в пространстве
2
2









5.7
Многогранники. Их свойства. Площади. Объемы
2
2









5.8
Тема вращения. Площади. Объемы
2
2









5.9
Методика обучения решению геометрических задач 7 – 9, 10 – 11 кл.
8
4
2
2



5.10
Решение задач координатой и векторным методом
4
2



2



VI
Цели. Содержание, методика обучения учащихся вопросам тригонометрии
14
6



8
Семинар

6.1
Выражения. Условия их существования. Тригонометрические выражения. Тригонометрические тождества. Формулы
4
2



2



6.2
Тригонометрические функции, свойства, графики
4
2



2



6.3
Тригонометрический круг и числовая программа в решении упражнений и задач по тригонометрии
4
2



2



6.4
Тригонометрические уравнения и неравенства системы
2






2



VII
Технологии обучения учащихся математике
16
12
2
2
Реферат

7.1
Концептуальные основы и показатели современного урока. Типы и формы уроков.
2



2






7.2
Новые педагогические технологии: сущность, правила. Классификация
2
2









7.3
Процессуальный аспект теории развивающего обучения

2
2









7.4
Технология поэтапного формирования умственных действий П.Я. Гальперина
2
2









7.5
Технология организации общения учащихся на уроках КФО
2
2









7.6
Технология игрового обучения
2
2









7.7
Блочное изучение курса математики
4
2



2



VIII
Формы, методы, средства контроля за уровнем математической подготовки школьников
14
4
6
4
Круглый стол

8.1
Разнообразие форм итогового контроля
2



2






8.2
Текущий контроль за уровнем математической подготовки учащихся
2






2



8.3
Письменные работы по математике. Требования. Оценка
2
2









8.4
Тестирование. Содержание. Роль и место в системе контроля
2



2






8.5
Письменные и устные экзамены. Анализ экзаменационных работ
4
2



2



8.6
Организация и содержание текущего, итогового повторения. Подготовка учащихся к экзаменам
2



2






IX
Внеклассная работа по математике
8
6



2
Круглый стол

9.1
Цель. Организация и содержание внеклассной работы
2
2









9.2
Формы внеклассных и внешкольных занятий по математике
2






2



9.3
Факультативы. Цель, содержание. Роль
2
2









9.4
Школьный интеллектуальный марафон
2
2












Итого
168
90
78



X
Спецкурсы (по выбору)












Реферат

XI
Итоговый контроль: деловая игра, аукцион, семинар, зачеты, математическое моделирование, реферат, собеседование, тестирование, диагностирование, контрольная работа
12






12




учебная Программа

Введение



Перемены, происходящие в общественно-политической жизни страны, существенно изменяют требования общества к школе. Обновление содержания и развития альтернативных форм образования, разработка новых технологий обучения требуют от учителя глубоких теоретических знаний по предмету, развитию педагогического мышления, постоянного поиска творческих решений в обучении и воспитании школьников.

Предлагаемая программа и тематический план предназначены для проведения курсов повышения квалификации учителей математики основной и старшей школы. Программа ориентирует учителей на работу в условиях качественно новых требований, предъявляемых обществом к общеобразовательной школе, знакомство с передовым опытом лучших учителей, повышение психолого-педагогического и общекультурного уровня.

Основным содержанием программы обучения учителей является углубление теоретической предметной подготовки, обновление знаний по методике преподавания предмета, по психолого-педагогическим вопросам, ознакомление с новыми технологиями обучения.

В настоящее время приоритетной линией образования является развитие детей. Поэтому в программе уделяется особое внимание процессуальным аспектам теории развивающего обучения Д.В. Эльконина – В.В. Давыдова, П.Я. Гальперина.

Нашли отражение в программе вопросы демократизации и гуманизации учебно-воспитательной работы в школе, новые подходы в работе на основе педагогического сотрудничества.

Занятия на курсах предлагается проводить в форме лекций, практикумов, консультаций, семинаров, моделирования уроков, деловых и ролевых игр и т. п.

В заключение курсов предлагается проведение зачетной работы по математике, защита рефератов, собеседование с учетом возможностей каждого слушателя.

Содержание занятий


Тема 1. Концепция школьного математического образования.

Основные направления развития школьного математического образования.

Новая философия образования, психология обучения. Роль математики в гуманизации образования.

Преподавание математики в условиях перехода на новый базисный учебный план. Место математики в нем.

Обязательный минимум содержания образования за курс основной школы как компонент государственного стандарта.

Содержательные линии школьного курса математики.

Перспективы развития содержания математического образования.

Актуальные проблемы преподавания математики на современном этапе.

Тема 2. Развитие понятия число, числа и выражения.

Методика формирования понятия числа в курсе математики 5 – 6 классов.

Методика формирования числа в курсе математики 7 – 9 классов.

Дальнейшее развитие понятия числа в курсе алгебры и начал анализа.

История возникновения процента как части числа. Понятие процента.

Методика решения задач на проценты, смешивание растворов и соединение сплавов.

Применение методов математического анализа при решении задач на проценты.

Конкурсные задачи на проценты.

Методика решения текстовых задач (арифметические и алгебраические способы решений).

Тема 3. Тождественные преобразования в курсе алгебры.

Выражение. Виды выражений. Степень. Одночислительное. Многочислительное.

Алгебраическая дробь. Арифметический квадратный корень, его свойства. Формулы сокращенного умножения и деления.

Тождественные преобразования всех видов выражений.

Функциональные и алгебраические методы в математике.

Уравнения – простейшая модель взаимосвязи величин.

Понятие об алгебраических уравнениях и неравенствах с параметрами и их системах.

Простейшие уравнения и неравенства с параметрами.

Знакомство с основными постановками задач с параметрами, методами их решения. Рекомендации по подбору задач для общеобразовательного уровня, для углубленного изучения, для факультативной работы.

Графическая интерпретация решений уравнений, неравенств, систем уравнений и неравенств.

Свойства функций в задачах с параметрами.

Модуль в алгебре и математическом анализе.

Систематизация материала, связанного с понятием модуля, числа и аспектами его применения.

Рассмотрение различных методов решения уравнений и неравенств с модулем, основанных на его определении, свойствах и графической интерпретации.

Выделение вопросов приложения модуля к преобразованию корней и к обеспечению равносильности уравнений.

Изложение теории вопросов параллельно решению задач.

Функции и их графики.

Определение функции, аргумента, значение функции, область определения функции.

Элементарные функции, их свойства, графики.

Тема 4. Основы математического анализа.

Концепция непрерывности в анализе, производная функции и ее применение к исследованию функций. Первообразная, применение первообразной в вычислению площадей.

Показательная, логарифмическая и степенная функции.

Методика их изучения в курсе алгебры и началах анализа.

Тема 5. Формирование геометрических знаний, умений.

Планиметрия. Аксиоматика. Плоскостные фигуры, из свойства. Доказательства. Решение геометрических задач. Построение геометрических фигур.

Планиметрия при решении стереометрических задач.

Многогранники. Круглые тела. Площадь поверхности. Объемы. Сечения. Вектор и его координаты. Применение метода координат при решении геометрических задач. Расстояние и углы между определяющими прямыми. Углы между прямыми и плоскостями. Методика изучения темы: «Декартовые координаты», «Векторы в пространстве».

Тема 6. Тригонометрический круг и числовая прямая в решении задач по тригонометрии.

Понятие тригонометрического круга. Запись чисел, соответствующих точкам окружности (5 случаев). Анализ тригонометрических функций.

Простейшие тригонометрические неравенства. Основные типы тригонометрических уравнений. Тригонометрические уравнения, содержащие модуль, параметры.

Решение нестандартных тригонометрических задач и помощью тригонометрического круга и числовой прямой.

Тема 7. Урок математики в современной школе.

Элементы демократизации и гуманизации в учебном процессе.

Новые аспекты в проведении традиционных уроков.

Организация уроков нового типа.

Творческие приемы обучения.

Моделирование уроков.

Педагогический анализ урока (видеоуроков).

Тема 8. Анализ результатов экзаменов.

Сообщаются итоги проверки областной комиссией работ, представленных на золотые и серебренные медали. Раскрываются недочеты, допущенные в теоретическом обосновании, неточность или избыточность обоснований. Показываются различные подходы к обоснованию заданий. Рассматриваются и анализируются тексты для гуманитарных и математических классов, основные и дополнительные тексты.

Предлагаются методические рекомендации по организации обобщающего повторения по содержательным линиям курса.

Тема 9. Внеклассная работа по математике.

Организация и содержание внеклассной и внешкольной работы по математике.

Формы внеклассных и внешкольных занятий по математике.

Факультутивы.

Тема 10. Спецкурсы по выбору.

Спецкурс 1.

Теория вероятностей и математическая статистика.

Цель: Способствовать выработке вероятностного мышления.

Задачи: познакомить слушателей со стахостической линией в математике и формой изложения ее основ.

Содержание:

Введение понятия случайного события. Различные подходы к определению вероятности.

Алгебра событий и теория о полной вероятности.

Повторение независимых событий, формула Бернулли.

Знакомство с простейшими законами распределения.

Числовые характеристики случайной величины.

Функциональная и корреляционная зависимость случайных величин.

Методы статистического анализа.

Методические рекомендации по распределению материала в школьной программе и по выбору задач в курсе математики основной школы.

Спецкурс 2.

Система учебной работы по формированию познавательной деятельности школьников.

Общие и специфические виды познавательной деятельности.

Логические приемы мышления (сравнение, подведение под понятие, выведения следствия из факта принадлежности объекта к данному понятию, приемы доказательств, классификации и т. д.).

Работа с определениями понятий. Доказательство логико-математических утверждений.

Поэтапное формирование умственных действий. Основные закономерности процесса усвоения знаний.

Спецкурс 3.

Методика решения задач, вызывающих трудности у выпускников школ при поступлении в ВУЗы.

Цель: повысить математическую культуру в области решения конкурсных задач.

Содержание:

Решение стереометрических задач на наибольшее и наименьше значение с использование производной.

Расстояние между скрещивающимися прямыми.

Методика решения задач на комбинацию многогранников и круглых тел.

Исследование квадратного трехчлена с параметрами. Применение исследований к решению задач повышенной трудности.

Спецкурс 4.

Повышение эффективности преподавания математики в сельской малочисленной школе.

Содержание:

Специфика урока к сельской малочисленной школе.

Выявление и учет возможностей и интересов учащихся в процессе преподавания математики в малочисленной школе.

Индивидуализация деятельности учащихся как основа дифференцированного обучения математике.

Методика отбора индивидуальных заданий с учетом возможностей учащихся.

Повышение роли творческих заданий, способствующих созданию атмосферы поиска, проявлению инициативы, развитию наблюдательности, внимания.

Организация коллективной деятельности учащихся при обучении математики в малочисленной школе.

Эффективные формы работы по формированию устойчивого интереса к предмету.

Тема 11. Итоговый контроль.

Итоговые разноуровневые зачетные работы для слушателей, отражающих тематику курсов, их анализ с целью осуществления срочной обратной связи и корректировка содержания последующих курсов.

В целях эффективности курсовой подготовки слушателей предлагается при поступлении на курсы проводить собеседование (примерные вопросы прилагаются) (выявление потребности и возможности слушателя) тестирование.

Во время курсов – применение различных форм обратной связи.

По окончании курсов слушатели защищают рефераты (тематика рефератов прилагается), а также могут сдать зачет по практическому курсу математики 5 – 11 класс.

Например:

Зачет № 1
  1. Решите неравенство

(17 х – 4 х2 – 4) • lg2 (х – 1) < 0
  1. Найдите все корни уравнения sin 2 х + cos х + 2 sin х = - 1, удовлетворяющее условию 0 < х < 5
  2. Изобразите на координатной плоскости линию, задаваемую уравнением

|у| = - х2 + 2 |х| + 3 и найдите площадь фигуры, ограниченной этой линией.
  1. Население области, состоящее из двух районов, составляет 800 тыс. человек. Через год прирост населения в первом районе составил 10 тыс. человек, а во втором районе – 9 тыс. человек. Каков процент прироста населения в каждом районе, если, известно, что в первом районе этот процент был не единицу меньше, чем во втором?
  2. Дан треугольник со сторонами 12 см, 15 см, 18 см. Проведена окружность, касающаяся обоих меньших сторон и имеющая центр на большей стороне. Найти отрезки, на которые цент окружности делит большую сторону треугольника.
  3. Укажите все значения параметра «а», при которых система уравнений имеет единственное решение. Найти это решение при каждом «а».



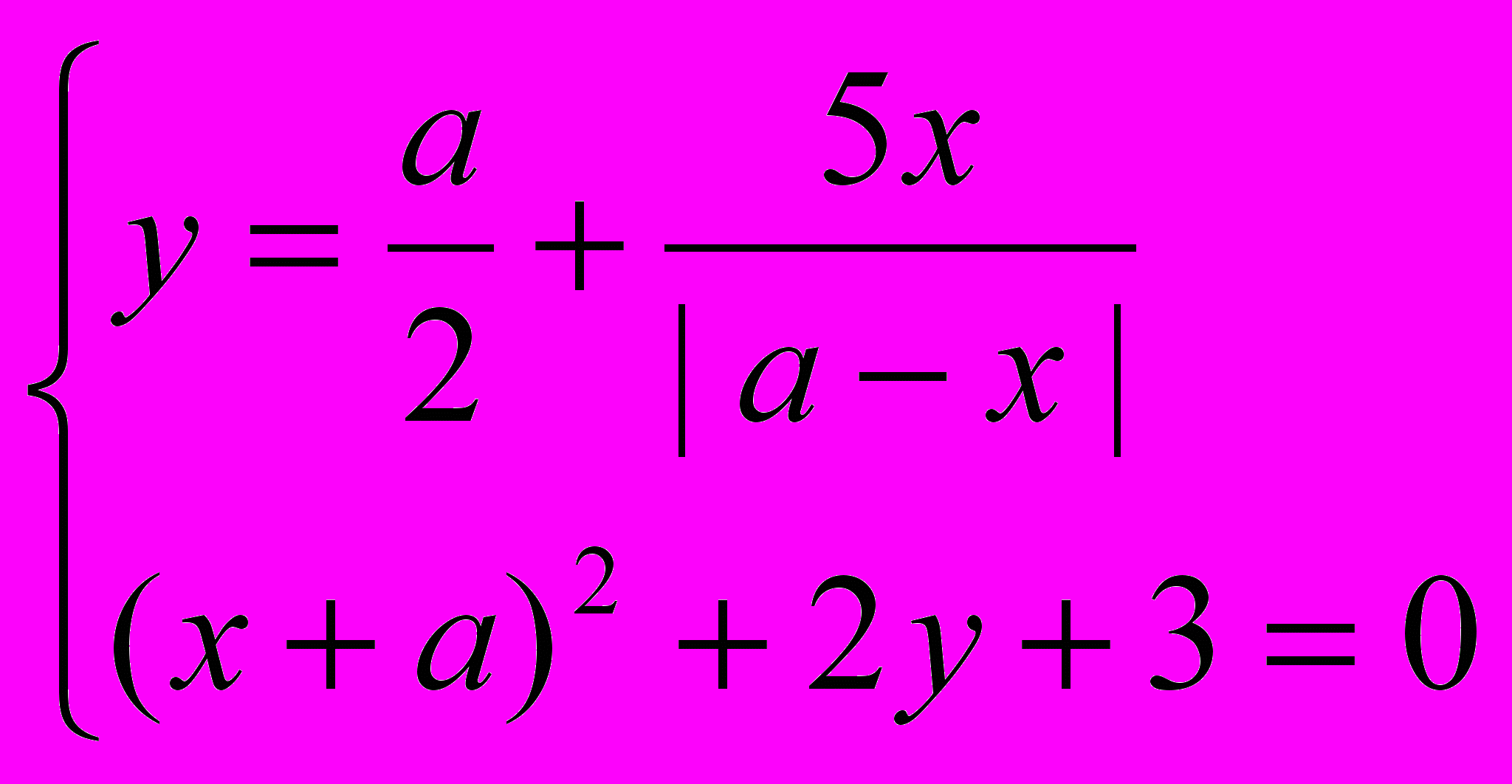
Контрольные задания

Контрольные вопросы:
  1. Знание задач преподавания математики на современном этапе развития общеобразовательной школы, глубокое и всестороннее знание действующих программ, учебников и учебных пособий.
  2. Знание теоретических основ методики преподавания математики, как педагогической науки.
  3. Знание путей практического осуществления воспитания учащихся в процессе обучения математики.
  4. Знание «трудных мест» школьной программы, понимание природы трудностей (содержательная, психологическая, методическая и т. п.).
  5. Готовность вести один из факультативных курсов математики, другая форма внеклассной работы.
  6. Функциональное владение методикой преподавания (умение, опираясь на основные положительные дидактики, возрастной и педагогической психологией, выбрать оптимальный вариант обучения в определенных условиях, умение в нужный момент заменить один прием обучения другим, не предусмотренным планом урока.
  7. Умение решать стандартные задачи по школьному курсу математики и обучение решению задач учащихся.
  8. Умение пробудить и развить интерес к математике, стимулировать у учащихся познавательную активность.
  9. Наличие навыков общения с техническими средствами обучения.
  10. Умение изготовлять и применять средства наглядности.
  11. Наличие навыков руководства внеклассной работой по математике.
  12. Знакомство с опытом учителей – новаторов. Использование его в практической работе.



Темы рефератов
  1. Формы и методы изложения новых знаний на уроках математики 5 – 9, 10 – 11 классы.
  2. Блочное изучение курса геометрии 9, 10 – 11 классы.
  3. Формы проверки домашнего задания.
  4. Тестовый контроль в 5 классе за уровнем математической подготовки.
  5. Развитие творческих способностей учащихся в 5 классе.
  6. Развитие логического мышления средствами математики.
  7. Развитие абстрактного мышления средствами математики.
  8. Повторительно-обобщающие уроки геометрии 9, 11 классы.
  9. Дифференцированный подход в обучении математики 5 – 9, 10 – 11 классы.
  10. Модульное изучение курса математики 10 – 11 класс.
  11. Элементы историзма на уроках математики.
  12. Эстетическое воспитание на уроках математики.
  13. Производная и ее применение.
  14. Тригонометрические функции.
  15. Показательные и логарифмические функции.
  16. Олимпиадные задания 5 – 6 класс.
  17. Олимпиадные задания 7 – 8 класс.
  18. Олимпиадные задания 10 – 11 класс.
  19. Самостоятельная работа. Роль, место в структуре урока.
  20. Домашние контрольные работы.
  21. Организация и содержание внеклассной работы по математике в 5 – 9, 10 – 11 классах.
  22. Отработка вычислительных навыков (содержание, методы, формы, средства).
  23. Роль наглядных средств в обучении школьников математике.
  24. Дидактические, раздаточные материалы. Роль и место на уроке математики.
  25. Формы и методы контроля за знаниями и умениями учащихся по математике:
  • письменный;
  • устный;
  • зачеты;
  • реферат;
  • собеседование.
  1. Виды учебных занятий по математике. Роль, актуальность, результативность.


Литература
  1. Геометрия Лобачевского. Авт. Атаносян Л.С.
  2. Домашняя математика: 7 класс, 8 класс, 9 класс. Авт. Ткачева М.В.
  3. Дополнительные главы к школьному учебнику алгебры 8 и 9 класс. Авт. Макарычев Ю.М.
  4. Дополнительные главы к школьному учебнику геометрии. Авт. Атанасян Л.С.
  5. За страницами учебника алгебры (для учащихся 7 – 9 класса). Авт. Пичурин Н.Ф.
  6. За страницами учебника геометрии (для учащихся 7 – 9 класса). Авт. Семенов Е.Е.
  7. За страницами учебника математик (для учащихся 5 – 6 класс). Авт. Депман И.А., Вимыкин Н.А.
  8. За страницами учебника математики: арифметика, алгебра, геометрия (для учащихся 10 – 11 классов). Авт. Виленкин Н.Я., Шибаев Л.П.
  9. За страницами учебника математики: математический анализ. Вероятность. Старинные и занимательные задачи (для учащихся 10 – 11 классов). Авт. Шибаев Л.П., Шибаства З.Ф.
  10. Задача одна – решения разные. Авт. Готман Э.П., Скопец З.Л.
  11. Изучение геометрии в 7 – 9 классе. Авт. Атанасян Л.С. и др.
  12. Математика 5. Задачи на смекалку. Авт. Шарыгин И.Ф., Шевкин А.В.
  13. Математика 5. Книга для учителя. Авт. Суворова С.Б., Бунимович Е.А. и др.
  14. Математика для любознательных. Авт. Петров И.С.
  15. Математика и искусство. Авт. Волошинов А.В.
  16. Математика. Учебник – собеседник. Авт. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В.
  17. Математические олимпиады школьников 9, 10, 11 класс. Авт. Резниченко С.В., Купцов Л.П. и др.
  18. Начала анализа и математические модели в естествознании и экономике. Авт. Баврин И.И.
  19. Нескучные вычисления. Авт. Скворцов В.В.
  20. Ну-ка, реши! Авт. Гриценко Н.П.
  21. О тригонометрии и не только о ней. Авт. Пичугин А.Ф.
  22. Обучение математическим доказательствам в школе. Авт. Саранцев Г.И.
  23. Прикладные задачи по алгебре 7 – 9 класс. Авт. Фоминых Ю.Ф.
  24. Решение типовых задач по геометрии 10 – 11 класс. Авт. Литвиненко В.М.
  25. Русская школа и математическое образование: Наша гордость и наша боль. Авт. Колягин Ю.М.
  26. Сборник задач по алгебре и началам анализа. Авт. Карт А.Г.
  27. Сборник задач по стереометрии с методами решения. Авт. Литвиненко В.М.
  28. Тестовые задания по алгебре для 9 класса. Пособие для учителя. Авт. Балашов Ю.В., Балашова Ю.М.
  29. Углубленное изучение алгебры и математического анализа. Авт. Галицкий М.Л. и др.
  30. Углубленное изучение геометрии в 10, 11 классе. Авт. Поповский В.М. т др.
  31. Углубленное изучение геометрии в 8, 9 классе. Авт. Окунев А.А.
  32. Журналы:
  • «Математика в школе»;
  • «Квант»;
  • «Наука и жизнь»;
  • «Алгебра и анализ».

Известия РАН. Серия математическая
  • математические заметки;
  • математический сборник;
  • математическое моделирование;
  • прикладная математика и механика;
  • успехи математических наук;
  • экономика и математические методы.

Газета «Математика».

Костромской областной институт повышения квалификации

работников образования



«Согласовано»

Начальник департамента общего

профессионального образования

администрации Костромской области

___________________ Тарабухин С.А.


«Утверждаю»