Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»

Вид материала

Учебное пособие

Содержание Лекция 5.Алгоритм Гаусса.Метод последовательного исключениянеизвестных

Подобный материал:

• Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
• Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
• Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
• Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
• Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
• Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
• Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
• Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.

Лекция 5.
Алгоритм Гаусса.
Метод последовательного исключения
неизвестных

Рассмотрим систему:


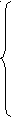а₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁

а₂₁x₁ + a₂₂x₂ + a₂₃x₃ + … + a_2nx_n = b₂ (1)

а₃₁x₁ + a₃₂x₂ + a₃₃x₃ + … + a_3nx_n = b<sub>3

…………………………………………………………</sub>

а_n1x₁ + a_n2x₂ + a_n3x₃ + … + a_nnx_n = b_n

Система не изменится, если

1. поменять местами любые 2 уравнения;
   
2. умножить правую и левую часть уравнения на одно и то же число (разумеется, не равное "0");
   
3. прибавить к одному уравнению другое, умноженное на любое число.
   

На этих утверждениях основан алгоритм Гаусса, который часто называют методом последовательного исключения неизвестных.

Сделаем 1-й шаг: будем умножать 1-е уравнение на такие числа, чтобы при сложении со всеми остальными уравнениями коэффициенты при х₁ во всех уравнениях, начиная со 2-го, обнулились. Другими словами, добьемся исключения неизвестного х₁ из всех уравнений, кроме 1-го.

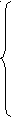а₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁

а₂₁x₁ + a₂₂x₂ + a₂₃x₃ + … + a_2nx_n = b₂ +(1)(- а₂₁/а₁₁)

а₃₁x₁ + a₃₂x₂ + a₃₃x₃ + … + a_3nx_n = b₃ +(1)(- а₃₁/а₁₁)

_{…………………………………………………………}

а_n1x₁ + a_n2x₂ + a_n3x₃ + … + a_nnx_n = b_n +(1)(- а_n1/а₁₁); а₁₁0

После 1-го шага получим систему в следующем виде:

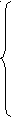а₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁

(2) a₂₂x₂ + a₂₃x₃ + … + a_2nx_n = b₂

a₃₂x₂ + a₃₃x₃ + … + a_3nx_n = b₃ +(2)( - а₃₂/а₂₂)

_{…………………………………………………………}

a_n2x₂ + a_n3x₃ + … + a_nnx_n = b_n +(2)( - а_n2/а₂₂); а₂₂0


На 2-м шаге будем добиваться исключения неизвестного х₂ из всех уравнений после 2-го. Для этого будем умножать 2-е уравнение на такое число, чтобы после сложения его с другими уравнениями, начиная с 3-го, коэффициенты при х₂ обнулились. После 2-го шага система преобразуется в следующий вид (3):




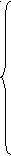
а₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁

(3) a₂₂x₂ + a₂₃x₃ + … + a_2nx_n = b₂

a₃₃x₃ + … + a_3nx_n = b₃

a₄₃x₃ + … + a_4nx_n = b<sub>4

…………………………………………………………</sub>

a_n3x₃ + … + a_nnx_n = b_n

Делая последовательно (n–1) шаг, мы исключим все неизвестные, кроме x_n, оставшегося в последнем уравнении.

После (n-1) шага система будет иметь следующий вид (4):

а₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁

(4) a₂₂x₂ + a₂₃x₃ + … + a_2nx_n = b₂

a₃₃x₃ + … + a_3nx_n = b<sub>3

………………………………………………………</sub>

a^(n-1) _nnx_n = b^(n-1) _n


(4) будем называть треугольным видом, причем 2-е уравнение осталось после 1-го шага, 3-е – после 2-го, 4-е – после 3-го и т.д., последнее  после (n-1) преобразования. На этом этап исключения неизвестных закончился. Видно, что теперь можно найти все неизвестные, начиная с x_n из последнего уравнения:

х_n=b_n^(n-1) / a_nn^(n-1)

Найденный x_n, подставленный в предпоследнее уравнение, даст х_n-1 и т. д. Двигаясь снизу вверх, по очереди будут найдены все n-неизвестные: (x_n, x_n-1, …, x₂, x₁).

Неизвестные исключаются так: (x₁, x₂, …, x_n), находились они в обратном порядке.

Если в результате преобразований на к-м шаге коэффициенты при неизвестных в некотором уравнении обнулились, а правая часть этого уравнения не равна 0, то преобразование необходимо прекратить, так как очевидно, что в этом случае система не совместна. Если же в результате преобразования в некотором уравнении обнулились и коэффициенты при неизвестных и правая часть, то такое уравнение следует вычеркнуть, т.е. оно не будет принимать участие в дальнейших преобразованиях. Таких уравнений может быть несколько. В этом случае система (1) не может быть приведена к треугольному виду (4), а может быть приведена к трапециевидному виду (5):


а₁₁x₁ + a₁₂x₂ + a₁₃x₃ + a₁₄x₄+ … + a_1nx_n = b₁

(5) a₂₂x₂ + a₂₃x₃ + a₂₄x₄ + … + a_2nx_n = b₂

a₃₃x₃ + a₃₄x₄ + … + a_3nx_n = b₃

a⁽³⁾₄₄x₄ + … + a⁽³⁾_4nx_n = b⁽³⁾ <sub>4

………………………………………………………</sub>

a^(к-1) _ккx_к + a^(к-1) _к,к+1x_к+1 + …+ a^(к-1) _кnx_n = b^(к-1) _n


Очевидно, что в этом случае система определена не однозначно, т. е. имеет бесконечное множество решений, связанных линейной зависимостью неизвестных (x_к, x_к+1, …, x_n).

Надо это понимать так: для всех (x_к, x_к+1, …, x_n) таких что a^(к-1) _ккx_к + a^(к-1) _к,к+1x_к+1 + …+ a^(к-1) _кnx_n = b^(к-1) _n, могут быть найдены все неизвестные, начиная с х_к-1 до х₁.

В некоторых частных случаях в системе (1) некоторые из диагональных коэффициентов (а₁₁, а₂₂, …, а_nn) могут быть равны 0.

Так, например, а₁₁=0. Тогда 1-й шаг, предполагающий вычисление а₂₁ / а₁₁, а₃₁ / а₁₁, …, а_n1 / а₁₁, невозможен. Это означает, что невозможно исключение неизвестного х₁. В этом случае можно поменять местами 1-е уравнение с любым другим, у которого коэффициент при неизвестном х₁ не равен 0, либо начать исключать неизвестные не с х₁, а с любого другого. При этом, если исключаются неизвестные в выбранном порядке, находить их необходимо в обратном выбранному порядке.

Так, например, имея систему линейных уравнений 5-го порядка (т.е. систему с 5-ю неизвестными), мы исключали неизвестные так:

(х₃, х_2, х_1, х₄, х₅)

Тогда находить их надо обязательно в обратном порядке:

(х₅х₄х₁х₂х₃)

Т.к. при решении системы методом Гаусса мы добиваемся обнуления коэффициентов при неизвестных, то, пользуясь данным алгоритмом и экономя время, обычно работают с матрицей коэффициентов. Такую матрицу называют расширенной матрицей системы: это матрица, составлена из коэффициентов при неизвестных с добавлением столбца свободных членов.

Пример.

х₁ + х₂ + х₃ + х₄ = 10

х₁ + 2х₂ + 3х₃ + 4х₄= 30

х₁ + 3х₂ + 4х₃ + 5х₄= 39

х₁ + 4х₂ + 5х₃ + 6х₄= 52


Составим расширенную матрицу системы и будем обнулять коэффициенты при х₁, х₂, х₃, начиная со 2-го , 3-го уравнения:

1	1	1	1	10				1	1	1	1	10			
1	2	3	4	30	-(1)			0	1	2	3	20
1	3	4	5	39	-(1)			0	2	3	4	29	-(2)2
1	4	5	6	52	-(1)			0	3	4	5	42	-(2)3

	1	1	1	1	10				1	1	1	1	10			
	0	1	2	3	20				0	1	2	3	20
	0	0	-1	-2	-11	(-1)			0	0	1	2	11
	0	0	-2	-4	-18	(-0,5)			0	0	1	2	9	-(3)

	1	1	1	1	10
	0	1	2	3	20
	0	0	1	2	11
	0	0	0	0	-2

Последняя строчка расширенной матрицы соответствует уравнению 0х₁ + 0х₂ + 0х₃ + 0х₄= -2, что невозможно не при каких х₁, х₂, х₃, х₄, следовательно, система несовместна.

Метод последовательного исключения неизвестных имеет преимущества перед методом Крамера:

1. быстродействие;
   
2. в случае бесконечного множества решений существует возможность указать линейную зависимость, образующую бесконечное множество решений. Другими словами метод Гаусса дает возможность описать бесконечное множество решений, а метод Крамера только констатирует факт;
   
3. методом можно пользоваться и в случае, когда число неизвестных не равно числу уравнений;
   
4. алгоритм Гаусса позволяет быстро вычислять определители высших порядков.