Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»

Вид материала

Учебное пособие

Содержание Лекция 2. Минор и алгебраическое дополнение. Основная теорема о разложении. Свойства определителей Основная теоремао разложении определителя

Подобный материал:

• Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
• Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
• Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
• Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
• Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
• Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
• Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
• Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.

Лекция 2.
Минор и алгебраическое дополнение.
Основная теорема о разложении.
Свойства определителей

Минор и алгебраическое дополнение

Рассмотрим элемент а_ij в определителе III порядка. При вычеркивании i-строки и j-столбца не вычеркнутыми останется определитель II порядка. Этот определитель II порядка будем называть минором элемента a_ij и обозначать M_ij. Таким образом, каждому элементу соответствует минор.

Например, дан определитель

a11	a12	a13
a21	a22	a23
a31	a32	a33

Рассмотрим элемент а₁₂. После вычеркивания 1-й строки и 2-го столбца остался не вычеркнутым определитель

а21	а23	=М12
а31	а33

Алгебраическим дополнением элемента называется определитель минора этого элемента, взятый со знаком «+», если сумма номера строки и номера столбца – четное число; «-», если сумма номера строки и номера столбца – нечетное число.

Будем обозначать алгебраическое дополнение А_ij.

А_ij = ΔM_ij (- 1)^i+j

Так, например, А₁₂ = - ΔМ₁₂, т.к. 1+2=3,(-1)³ = -1

Основная теорема
о разложении определителя

Теорема: Определитель равен алгебраической сумме произведений элементов любой строки или столбца на их алгебраические дополнения.

Другими словами, определитель может быть разложен по любой строке или столбцу.

Доказательство: Разложим определитель III порядка по 1-й строке или по 2-му столбцу. Так как определитель – это число, то очевидно, что при любом разложении должно получиться одно и то же число.

а11	а12	а13	= а11А11 + а12А12 + а13А13 =
а21	а22	а23
а31	а32	а33
=а11	а22	а23	- а12	а21	а23	+а13	а21	а22	=
	а32	а33		а31	а33		а31	а32
=а11(а22а33 – а32а23) – а12(а21а33 – а31а23) + а13(а21а32 – а31а22)=
= a11a22a33 – a32a23a11 – a33a21a12+ a12a23a31 + a13a21a32 – a31a22a13

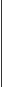
а11	а12	а13	= а12А12 + а22А22 + а32А32 =
а21	а22	а23
а31	а32	а33
= - а12	а21	а23	+ а22	а21	а23	- а32	а11	а13	=
	а31	а33		а31	а33		а21	а23
= - а12(а21а33 – а31а23) + а22(а21а33 – а31а23) – а32(а11а23 – а21а13)=
=– a33a21a12 + a12a23a31 + a11a22a33 – a31a22a13 – a32a23a11 + a13a21a32

Нетрудно видеть, что результат получился одинаковый (т.е. выбор строки или столбца не влияет на результат). Кроме того, если сравнить данный результат с вычисленным по правилу Саррюса (лекция 1), то видно, что они одинаковы.

Используя теорему о разложении, можно вычислять определители.

Например,

1	2	3	= 7	2	3	- 8	1	3	+ 9	1	2	=
4	5	6		5	6		4	6		4	5
7	8	9
= 7(12 – 15) – 8(6 – 12) + 9(5 – 8) =
= 7( - 3) – 8( – 6) +9( - 3) = - 3 (7 – 16 +9)=0

О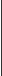собенно рационально использовать теорему о разложении в случае, когда в строке или столбце есть нулевые элементы.

1	0	3	= 5	1	3
4	5	6		7	9	= 5(9 – 21) = - 60
7	0	9

Раскладывая данный определитель по 2-му столбцу, все произведения элементов на их алгебраические дополнения равны «0», так как сами элементы равны нулю, кроме одного а₂₂ = 5.