Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»

Вид материала

Учебное пособие

Содержание Лекция 4.Системы линейных уравнений.Метод Крамера Решением системы Метод Крамера Таким образом, система (1) преобразовалась в систему 2) – называются уравнениями Крамера. Эти уравнения (2) позволяют найти единственное решение системы (3) в случае, когда Очевидно, что система в этом случае не определена однозначно, т.е. существует бесконечное множество решений. Составим и вычислим добавочные определители Δх , Δх , Δх . х2= Δх /Δ х3= Δх /Δ , т.е.

Подобный материал:

• Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
• Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
• Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
• Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
• Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
• Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
• Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
• Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.

Лекция 4.
Системы линейных уравнений.
Метод Крамера

Системой линейных уравнений n-ного порядка называется система следующего вида:

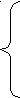а₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁

а₂₁x₁ + a₂₂x₂ + a₂₃x₃ + … + a_2nx_n = b₂

………………………………………

а_m1x₁ + a_m2x₂ + a_m3x₃ + … + a_mnx_n = b_m


(x₁, x₂, …x_n) – n неизвестных, связанных между собой линейной зависимостью;

(b₁, b₂, …b_m) - свободные члены;

a_ij – коэффициенты при j- неизвестных в i-м уравнении.

Видно, что в системе m уравнений и n неизвестных. В общем случае mn.

Решением системы называются конкретные числа (x₁^*, x₂^*, x₃^*_{, …,} x_n^*), при подстановке которых в систему уравнения обращаются в тождества.

Система называется однородной, если свободные члены уравнений все равны «0».

Система может иметь одно или бесконечное множество решений. В этом случае систему будем называть совместной определенной или соответственно совместной неопределенной.

Система может не иметь ни одного решения. Такую систему будем называть несовместной. Однородная система всегда совместна, т.к. имеет, по крайней мере, одно решение. Действительно, если в уравнение однородной системы подставить х₁=0, x₂=0, …, x_n=0, то все уравнения обратятся в тождества 00.

Такое нулевое решение (0, 0,….,0) будем называть тривиальным. Тем не менее, однородную систему исследуют для нахождения других, нетривиальных решений, конечно, если они существуют.

Существуют различные методы решения систем линейных уравнений.

Метод Крамера

Рассмотрим систему:


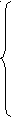а₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁

а₂₁x₁ + a₂₂x₂ + a₂₃x₃ + … + a_2nx_n = b₂ (1)

а₃₁x₁ + a₃₂x₂ + a₃₃x₃ + … + a_3nx_n = b<sub>3

…………………………………………………………</sub>

а_n1x₁ + a_n2x₂ + a_n3x₃ + … + a_nnx_n = b_n

Главным определителем системы Δ будем называть определитель n-го порядка, составленный из коэффициентов при неизвестных x_j, т.е.

Δ=	а11	а12	…	а1n
	a21	a22	…	a2n
	а31	а32	…	а3n
	- - - - - - - - - - - - - - - - - - - -
	an1	an2	…	ann

b1	- правые части всех уравнений (свободные члены) назовем столбцом свободных членов.
b2
b3

bn

Из школьного курса известно, что правую и левую часть уравнений можно умножить на одно и то же число, а также уравнения системы можно складывать (вычитать) друг с другом. От этого система не изменится.

Тогда умножим правую и левую часть 1-го уравнения системы на алгебраическое дополнение А₁₁ элемента а₁₁ главного определителя Δ; правую и левую часть 2-го уравнения  на А₂₁ элемента а₂₁ и т.д., а затем сложим все уравнения. Имеем:




а₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁ А₁₁

+ а₂₁x₁ + a₂₂x₂ + a₂₃x₃ + … + a_2nx_n = b₂ А<sub>21

…………………………………………………………</sub>

а_n1x₁ + a_n2x₂ + a_n3x₃ + … + a_nnx_n = b_n A_n1




(a₁₁A₁₁+a₂₁A₂₁+…+a_n1A_n1)x₁ + (a₁₂A₁₁+a₂₂A₂₁+…+a_n2A_n1)x₂ + …. +(a_1nA₁₁+a_2nA₂₁+…+a_nnA_n1)x_n = b₁A₁₁+b₂A₂₁+…+b_nA_n1

Таким образом, каждое уравнение системы было умножено соответственно на алгебраические дополнения элементов 1-го столбца главного определителя Δ. После сложения видно, что при неизвестном х₁ имеем коэффициент, равный алгебраической сумме произведений элементов 1-го столбца определителя Δ на их алгебраические дополнения. По теореме о разложении определителя такая алгебраическая сумма равна определителю Δ. При всех остальных неизвестных, начиная со второго: (х₂, х₃, …,х_n), коэффициенты соответственно равны алгебраическим суммам произведений элементов 2-го, 3-го, …, n-го столбцов на алгебраические дополнения элементов 1-го столбца. Такие алгебраические суммы по свойству 7 равны "0". Таким образом, в левой части осталось только одно неизвестное х₁. В правой части уравнения – алгебраическая сумма, соответствующая разложению определителя, у которого 1-й столбец – столбец свободных членов:

b1	a12	…	a1n	=Δx 1
b2	a22	…	a2n
			
bn	an2	…	ann

Δ_х - добавочный при неизвестном х₁. Таким образом, имеем

¹

Δх₁=Δ_х

¹

Если правую и левую части каждого уравнения системы (1) умножить на алгебраические дополнения элементов 2-го столбца соответственно, а затем сложить, то в левой части уравнения–суммы обнулятся коэффициенты при всех неизвестных, кроме х2. Коэффициент при неизвестном х2 будет равен:

a₁₂A₁₂ + a₂₂A₂₂ +…+ a_n2A_n2 = Δ

Это главный определитель Δ, разложенный по элементам 2-го столбца.

В правой части уравнения–суммы будем иметь

b₁A₁₂+b₂A₂₂+…+b_nA_n2,

что соответствует разложению по второму столбцу определителя

a11	b1	…	a1n	=Δx 2
a21	b2	…	a2n
			
an1	bn	…	ann

Δ_х - добавочный при неизвестном х₂.

²

Далее, если умножить правую и левую часть уравнений на алгебраические дополнения 3-го, 4-го, …, n-го столбцов, а затем сложить, то очевидно, что этими действиями исключим по очереди все неизвестные, кроме (х₃, х₄,…,x_n). Нетрудно видеть, что все добавочные определители – это определители, полученные из главного путем замены соответствующего столбца на столбец свободных членов.

Таким образом, система (1) преобразовалась в систему:

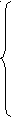
Δх₁=Δ_х

¹

Δх₂=Δ_х (2)

<sup>2

…………………</sup>

Δх₁=Δ_х

ⁿ

(2) – называются уравнениями Крамера. Эти уравнения (2) позволяют найти единственное решение системы (3) в случае, когда

Δ0, Δ_х 0, Δ_х 0,…, Δ_х 0,

^{1 2 n}

а также исследовать систему на совместность.

х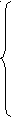₁= Δх /Δ

¹

х₂= Δх /Δ (3)_

²

…………

х_n= Δх /Δ

ⁿ

Итак, справедливы следующие 4 случая:

1. Δ0, Δ_х 0, Δ_х 0,…, Δ_х 0,

^{1 2 n}

Система совместна и определена, т.е. имеет единственное решение (3).

2. Δ=0, Δ_х 0, Δ_х 0,…, Δ_х 0,

^{1 2 n}

В этом случае система не совместна.

3. Δ0, Δ_х =0, Δ_х =0,…, Δ_х =0,

^{1 2 n}

Система имеет тривиальное решение.

4. Δ=0, Δ_х =0, Δ_х =0,…, Δ_х =0,

^{1 2 n}

Уравнения Крамера (2) обращаются в этом случае в следующий вид:

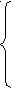0х₁ =0

0х₂ =0

………

0х_n =0

Очевидно, что система в этом случае не определена однозначно, т.е. существует бесконечное множество решений.

Пример 1. Решить систему методом Крамера.


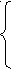х₁ + х₂ – х₃ = 3

х₁ + 2х₂ + 3х₃ = - 4

- 2х₁ – х₂ + х₃ = 0


Главный определитель Δ – определитель, составленный из коэффициентов при х₁, х₂, х₃

	1	1	- 1
Δ=	1	2	3	= - 5
	- 2	- 1	1

Составим и вычислим добавочные определители

Δ_х , Δ_х , Δ_х .

^{1 2 3}

Столбец свободных членов	3
	- 4
	0

по очереди подставим вместо 1-го, 2-го и 3-го столбцов определителя Δ.

Имеем,		3	1	- 1
	Δх = 1	- 4	2	3	=15
		0	-1	1
		1	3	- 1
	Δх = 2	1	- 4	3	= - 17
		- 2	0	1
		1	1	3
	Δх = 3	1	2	- 4	= 13
		- 2	- 1	0

Ни один из определителей не равен "0", следовательно, система однозначно определена и решение ее:

х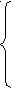₁= Δх /Δ

¹

х₂= Δх /Δ

²

х₃= Δх /Δ , т.е.

³

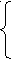х₁ = - 3

х₂ = 17/5

х₃ = - 13/5

Сделаем проверку:

• 3 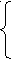+17/5 +13/5 =3
  
• 3 +2  17/5 +3 (- 13/5) =- 4
  
• 2 (-3) – 17/5 – 13/5 =0
  

Уравнения обратились в тождества. Следовательно, решение найдено верно.