Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»
| Вид материала | Учебное пособие |
СодержаниеЛекция 10. Теорема Кронекера – Копелли. Решение произвольных системлинейных уравнений |
- Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
- Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
- Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
- Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
- Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
- Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
- Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
- Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
- Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
- Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.
Лекция 10.
Теорема Кронекера – Копелли.
Решение произвольных систем
линейных уравнений
Произвольной системой линейных уравнений называется система следующего вида:
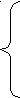 а11x1 + a12x2 + … + a1nxn = b1
а11x1 + a12x2 + … + a1nxn = b1(1) а21x1 + a22x2 + … + a2nxn = b2
………………………………………
аm1x1 + am2x2 + … + amnxn = bm
Матрицей системы А называется матрица, составленная из коэффициентов при неизвестных
| А  = = | а11 | а12 | … | а1n |
| а21 | а22 | … | а2n | |
| …………………. | ||||
| аm1 | аm2 | … | аmn | |
Расширенной матрицей А системы называется матрица(АВ) – это матрица А, к которой добавлен столбец свободных членов:
| А  = = | а11 | а12 | … | а1n | b1 |
| а21 | а22 | … | а2n | b2 | |
| ......................................... | |||||
| аm1 | аm2 | … | аmn | bm | |
Справедлива следующая теорема Кронекера – Копелли:
Система совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.
Эта теорема лежит в основе методики исследования и нахождения решения произвольных систем.
Предположим, что rang(А)= rang(А)=r, т.е. система (1) совместна, тогда любой минор r-го порядка Мr0 может быть выбран в качестве базового минора.
Соответствующие ему неизвестные будут базовыми неизвестными, а оставшиеся неизвестные назовем свободными константами. Для определенности изложения, предположим, что Мr0 соответствует первым неизвестным: (х1, х2,..., хr), которые, таким образом, являются базовыми, тогда (хr+1, хr+2,..., хn) – свободные константы.
Перепишем систему (1) в соответствии с выбранным Мr
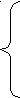 а11x1 + a12x2 + … + a1rxr = b1 - a1,r+1xr+1 - ... - a1nxn
а11x1 + a12x2 + … + a1rxr = b1 - a1,r+1xr+1 - ... - a1nxn(2) а21x1 + a22x2 + … + a2rxr = b2- a2,r+1xr+1 - ... – a2nxn
………………………………………
аr1x1 + ar2x2 + … + arrxr = br- ar,r+1xr+1 - ... – arnxn
Все уравнения, начиная с (r+1), откинуты, т.к. они являются линейными комбинациями первых r. Это стало известно после вычисления рангов А и А. Все свободные константы перенесены в правые части уравнений со своими коэффициентами с противоположными знаками.
Система (2) имеет основную матрицу или главный определитель =Мr0, следовательно, по правилу Крамера (2) совместна и имеет бесконечное множество решений, зависящих от свободных констант хr+1=c1, хr+2=c2,..., хn=cn-r.
Общее решение системы может быть записано в виде (3)
| | x 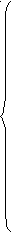 1=x(c1, c2,..., cn-r) / 1=x(c1, c2,..., cn-r) / 1 | |
|---|---|---|
| | x2=x(c1, c2,..., cn-r) / 2 | |
| (3) .............................................. | | |
| | xr=x(c1, c2,..., cn-r) / r | |
| | хr+1=c1 | |
| | хr+2=c2 | |
| | ............................................. | |
| | хn=cn-r | |
Из общего решения (3) может быть получено любое частное. Для этого необходимо присвоить свободным константам с1, с2,..., сn-r конкретные значения и вычислить х1, х2,..., хr
Пример.
-
х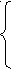 1-4х2+2х3= - 1
1-4х2+2х3= - 1
2х1-3х2-х3-5х4= - 7
3х1-7х2+х3-5х4= - 8


1
-4
2
0
1
-4
2
0
-1
rang
2
-3
-1
-5
=rang
2
-3
-1
-5
-7
=2
3
-7
1
-5
3
-7
1
-5
-8
(проверить самостоятельно)
Следовательно, по теореме Кронекера – Копелли система совместна и ее решение может быть записано через любой базовый минор 2-го порядка, не равный 0. Например,
-
М2=
1
-4
=5
2
-3
(минор находится в левом верхнем углу основной матрицы системы)
Выберем его в качестве базового минора. Тогда, неизвестные х1 и х2 – базовые, а х3,х4 – свободные константы.
Перепишем систему в соответствии с выбранным базовым минором:
 х1-4х2 = -1 – 2х3
х1-4х2 = -1 – 2х32х1-3х2 = - 7 +х3+5х4
Вычислим добавочные определители при базовых неизвестных х и х :
1 2
-
х=
1
-1 – 2х3
- 4
= 3+6х3-28+4х3+20х4=
- 7 +х3+5х4
- 3
= -25+10х3+20х4=-5(5-2х3-4х4)
х=
2
1
-1 – 2х3
=-7+х3+5х4+2+4х3=
2
- 7 +х3+5х4
=-5+5х3+5х4=- 5(1-х3-х4)
 Общее решение
Общее решение-
х1= х /=-5(5-2х3-4х4) / 5=-5+2х3+4х4
1
х2= х /=- 5(1-х3-х4) / 5=- 1+х3+х4
2
х3=с1
х4=с2
 Найдем какое-нибудь частное решение. Положим, например, с1 и с2 – нули, тогда
Найдем какое-нибудь частное решение. Положим, например, с1 и с2 – нули, тогдах1= -5
х2= -1
х3= 0
х4= 0
Если с1 и с2 – какие-нибудь другие величины, то в соответствии со свободными константами.
Например:
 х1= -1
х1= -1х2= -1
х3= 1
х4= 1 и т.д.
Мы можем в качестве базового минора выбрать любой другой
| М20. Например, М2= | 2 | 0 | = -10. |
| 1 | -5 |
Этот минор соответствует х3 и х4 в 1-м и в 3-м уравнениях.
Тогда система будет
 2х3=-1-х1+4х2
2х3=-1-х1+4х2х3-5х4=-8-3х1+7х2
-
х=
3
-1 – х1+4х2
0
= 5+5х1 +20х2=
- 8 -3х1+7х2
-5
= 5(1+х1+4х2)
х=
4
2
-1 – х1+4х2
=-16-6х1+14х2+1+х1-4х2=
1
- 8 -3х1+7х2
=-15-5х1+10х2=- 5(3+х1-2х2)
Общее решение при таких выбранных базовых неизвестных («в такой базе»):
 х1=с1 х1=с1 | |
| х2=с2 | |
| | х3= х /=5(1+х1+4х2) / (-10)=-1/2(1+х1+4х2) 3 |
| | х4= х /=- 5(3+х1-2х2) / (-10)=1/2(3+х1-2х2) 4 |
Если с1 и с2 – нули, то частное решение

х1=0
х2=0
х3=-1/2
х4=3/2
Из этого общего решения можно получить частное решение, полученное из любого другого, записанного «в любой другой базе».
Например,

х1=-5
х2=-1
х3=0
х4=0 может быть получено из последнего общего при х1=-5, х2=-1
 х1=-5
х1=-5х2=-1
х3= -1/2(1-5+4)=0
х4=1/2(3-5+2)=0
