Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»
| Вид материала | Учебное пособие |
Содержание2. Матрицы. Действия над матрицами.Матричные уравнения |
- Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
- Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
- Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
- Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
- Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
- Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
- Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
- Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
- Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
- Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.
2. Матрицы. Действия над матрицами.
Матричные уравнения
Вычислить:


| 2.1 | 3А + 2В, | А = | 2 | 1 | – 1 | , В = | – 2 | 1 | 0 |
| 0 | 1 | – 4 | – 3 | 2 | 2 |




| 2.2 | 3 | – 2 | 3 | 7 | 2.3 | 4 | 0 | – 2 | 3 | 1 | 3 |
| 5 | – 4 | 6 | – 1 | | | | | | 1 | ||
| 0 | 1 | | | | | | | | – 1 | ||
| | | | | | | | | | | 5 | |
| | | | | | | | | | | 2 |


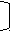




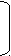
| 2.4 | 3 | 4 | 0 | – 2 | 3 | 1 | 2.5 | 0 | 0 | 1 | – 1 | – 1 | 4 | | ||||
| 1 | | | | | | 1 | 1 | 2 | 2 | 2 | 1 | | ||||||
| – 1 | | | | | | 2 | 2 | 3 | 1 | 1 | | |||||||
| 5 | | | | | | 3 | 3 | 4 | | | | | ||||||
| 2 | | | | | | | | | | | | |||||||
    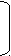 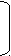 | | | 3 | | | n | | | n |
| 2.6 | 1 | – 2 | 2.7 | 1 | Q | 2.8 | | 1 | |
| | 3 | – 4 | | 0 | 1 | | 0 | | |

| 2.9 | f(x) = 3x2 – 4, | A = | 2 | 1 |
| 0 | 3 |
| 2.10 | АВ – ВА, | если А = | 2 | 3 | 1 | , В = | 1 | 2 | 1 |
| – 1 | 1 | 0 | 0 | 1 | 2 | ||||
| 1 | 2 | – 1 | 3 | 1 | 1 |

| 2.11. Найти все матрицы второго порядка, такие, что их квадраты равны нулевой матрице | 0 = | 0 | 0 |
| 0 | 0 |

| 2.12 | ААТ, если А = | 1 | 2 | 1 | 3 |
| 4 | – 1 | 5 | – 1 |
Вычислить обратную матрицу при помощи союзной


| 2.13 | 3 | 4 | 2.14 | cos | – sin |
| 5 | 4 | sin | cos |
    2.15 2.15 | 1 | 1 | 1 | 1 | 2.16 | 3 | – 4 | 5 |
| | 1 | 1 | – 1 | – 1 | | 2 | – 3 | 1 |
| | 1 | – 1 | 0 | 0 | | 3 | – 5 | – 1 |
| | 0 | 0 | 1 | – 1 | | | | |
Методом элементарных преобразований найти обратные матрицы:




| 2.17 | 1 | 2 | 2 | 2.18 | 1 | 1 | 1 | 1 |
| | 2 | 1 | – 2 | | 1 | 1 | – 1 | – 1 |
| | 2 | – 2 | 1 | | 1 | – 1 | 1 | – 1 |
| | | | | | 1 | – 1 | – 1 | 1 |
Решить матричные уравнения:


| 2.19 | 1 | 2 | Х | = | 3 | 5 |
| 3 | 4 | 5 | 9 |



| 2.20 | Х | 3 | – 2 | = | – 1 | 2 | ||||
| | 5 | – 4 | | – 5 | 6 | |||||



| 2.21 | 3 | – 1 | Х | 5 | 6 | = | 14 | 16 |
| 5 | – 2 | 7 | 8 | 9 | 10 |


| 2.22 | 1 | 2 | – 3 | Х = | 1 | – 3 | 0 |
| 3 | 2 | – 4 | 10 | 2 | 7 | ||
| 2 | – 1 | -0 | 10 | 7 | 8 |


| 2.23 | Х | 5 | 3 | 1 | = | – 8 | 3 | 0 | |
| 1 | – 3 | – 2 | – 5 | 9 | 0 | ||||
| – 5 | 2 | 1 | – 2 | 15 | 0 | ||||




| 2.24 | A2 B + C2 = D, A = | 1 | 1 | , B = | – 1 | 3 | , C = | 1 | –2 | , |
| 2 | 1 | 0 | 1 | 1 | 3 |

| D = | 3 | 4 |
| 0 | –1 |
