Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»
| Вид материала | Учебное пособие |
Содержание3. Решение систем линейных уравнений |
- Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
- Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
- Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
- Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
- Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
- Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
- Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
- Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
- Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
- Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.
3. Решение систем линейных уравнений
Решить системы линейных уравнений методом Крамера
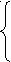
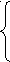
| 3.1 | 3x – 4y = – 6 | 3.2 | 3x – 5y = 13 |
| 3x + 4y = 18 | 2x + 7y = 81 |
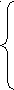
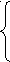
| 3.3 | 2ax – 3by = 0 | 3.4 | 2x + y = 5 |
| 3ax – 6by = ab | x + 3z = 16 | ||
| | | 5y – z = 10 |

| 3.5 | x + y – 2z = 6 | 3.6 | 2x1 + 5x2 + 4x3 + x4 – 20 = 0 |
| 2x + 3y – 7z = 16 | x1 + 3x2 + 2x3 + x4– 11 = 0 | ||
| 5x + 2y + z = 16 | 2x1 + 10x2 + 9x3 + 9x4 – 40 = 0 | ||
| | 3x1 + 8x2 + 9x3 + 2x4 – 37 = 0 |
Решить системы линейных уравнений методом Гаусса

| 3.7 | x1 + x2 + x3 + x4 + x5 = 15 |
| x1 + 2x2 + 3x3 + 4x4 + 5x5 = 35 | |
| x1 + 3x2 + 6x3 + 10x4 + 15x5 = 70 | |
| x1 + 4x2 + 10x3 + 20x4 + 35x5 = 126 | |
| x1 + 5x2 + 15x3 + 35x4 + 70x5 = 210 |

| 3.8 | 2x1 + 7x2 + 3x3 + x4 = 5 |
| x1 + 3x2 + 5x3 - 2x4 = 3 | |
| x1 + 5x2 - 9x3 + 8x4 = 1 | |
| 5x1 + 18x2 + 4x3 + 5x4 = 12 |
| 3.9 | 5x1 + 2x2 - 7x3 + 14x4 = 21 |
| 5x1 - x2 + 8x3 - 13x4 + 3x5 = 12 | |
| 10x1 + x2 - 2x3 + 7x4 - x5 = 29 | |
| 15x1 + 3x2 + 15x3 + 9x4 + 7x5 = 130 | |
| 2x1 - x2 - 4x3 + 5x4 - 7x5 = - 13 |
| 3.10 | 2x1 - x2 + x3 - x4 = 3 |
| 4x1 - 2x2 - 2x3 + 3x4 = 2 | |
| 2x1 - x2 + 5x3 - 6x4 = 1 | |
| 2x1 - x2 - 3x3 + 4x4 = 5 |
Указание: ввести неизвестное
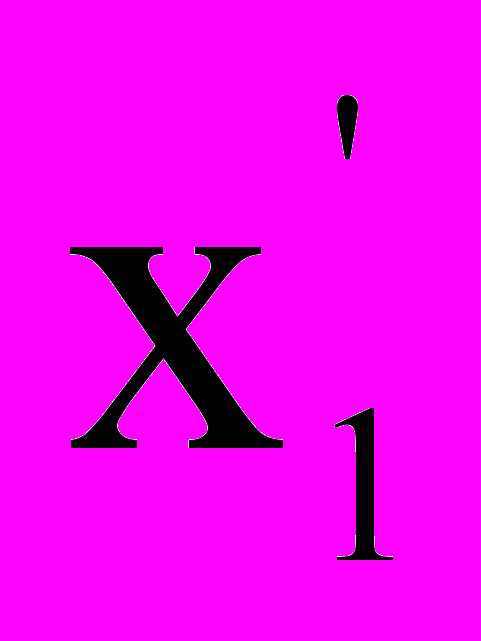 = 2x1
= 2x1Вычислить ранги следующих матриц:




| 3.11 | 2 | - 1 | 3 | - 2 | 4 | 3.12 | 25 | 31 | 17 | 43 |
| 4 | - 2 | 5 | 1 | 7 | 75 | 94 | 53 | 132 | ||
| 2 | - 1 | 1 | 8 | 2 | 75 | 94 | 54 | 134 | ||
| | | | | | | 25 | 32 | 20 | 48 |


| 3.13 | 0 | 1 | 1 | 0 | 0 | 3.14 | 0 | - 1 | 0 | 1 | 3 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | - 2 | 0 | - 1 | - 1 | ||
| 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | ||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | ||
| 0 | 0 | 1 | 1 | 0 | - 1 | - 3 | - 1 | 2 | 2 | 0 | ||
| | | | | | | 3 | 2 | - 1 | - 1 | - 1 | - 1 |
Решить произвольные системы, предварительно исследуя их на совместность
| 3.15 | 3x1 - 2x2 - 5x3 + x4 = 3 |
| 2x1 - 3x2 + x3 + 5x4 = - 3 | |
| x1 + 2x2 - 4x4 = - 3 | |
| x1 - x2 - 4x3 + 9x4 = 22 |
| 3.16 | 2x1 + 7x2 + 3x3 + x4 = 6 |
| 3x1 + 5x2 + 2x3 + 2x4 = 4 | |
| 9x1 + 4x2 + x3 + 7x4 = 2 |
| 3.17 | 3x1 + 2x2 + 2x3 + 2x4 = 2 |
| 2x1 + 3x2 + 2x3 + 5x4 = 3 | |
| 9x1 + x2 + 4x3 - 5x4 = 1 | |
| 2x1 + 2x2 + 3x3 + 4x4 = 5 | |
| 7x1 + x2 + 6x3 – x4 = 7 |
Исследовать совместность и найти общее решение в зависимости от значения параметра
| 3.18 | (1 + )x1 + x2 + x3 = 1 |
| x1 + (1 + )x2 + x3 = 1 | |
| x1 + x2 + (1 + )x3 = 1 |
