Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»

Вид материала

Учебное пособие

Содержание Бином Ньютона.Метод математической индукции Теорема Лапласа Алгебраическим дополнением минора k–го порядка Список рекомендуемой литературы

Подобный материал:

• Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
• Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
• Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
• Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
• Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
• Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
• Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
• Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.

Бином Ньютона.
Метод математической индукции

Формула бинома Ньютона:

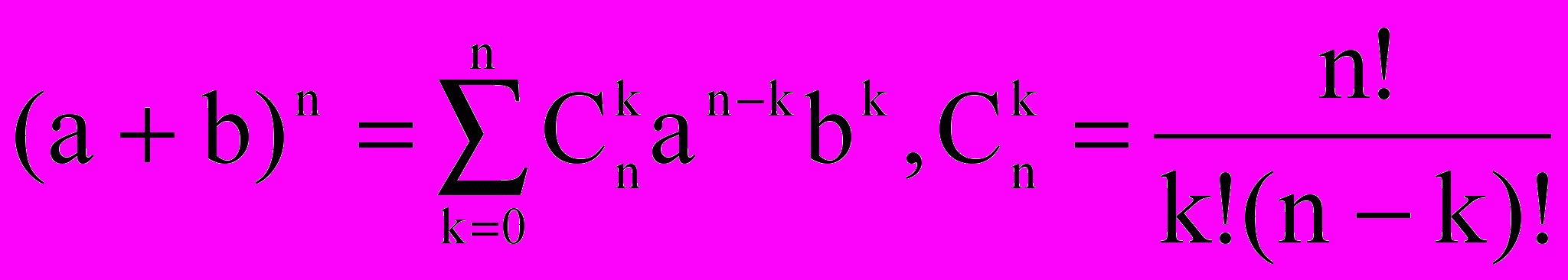- биномиальные коэффициенты

может быть доказана при помощи метода математической индукции.

Метод заключается в следующем:

1. проверяется справедливость утверждения при n = 1, 2, 3, 4, …;
   
2. делается предположение, что утверждение справедливо только до некоторого n;
   
3. доказывается, что утверждение справедливо для следующего (n – 1), а, следовательно, справедливо для любого n.
   

Этот метод основан на принципе, который является аксиомой арифметики натуральных чисел.

Продемонстрируем этот метод на примере.

Пример.

Доказать справедливость неравенства Я.Бернулли

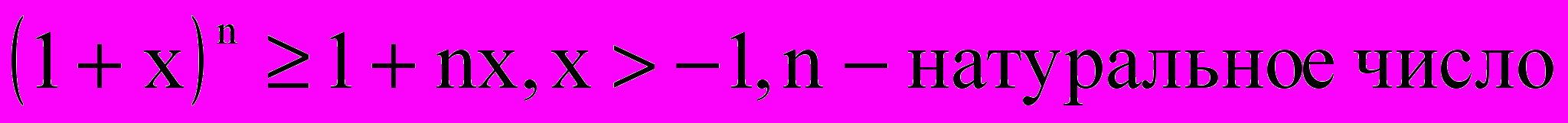1. При n = 1
   

(1 + x)¹ = 1 + x,

n = 2

(1 + х)² = 1 + 2х + х²  1 + 2х, т.к. х²  0

и так далее.

2. Предположим, что неравенство Я.Бернулли справедливо только для k членов натурального ряда
   

   (1 + x)k  1+ kx

   ()

3. Докажем, что неравенство () справедливо для следующего (k + 1) натурального числа. Умножим правую и левую часть неравенства () на
   (1 + х), т.к. (1 + х)  0 (по условию х  - 1), то неравенство не меняет знак:
   

(1 + x)^k+1  (1 + kx)(1 + x)

(1 + x) ^k+1  1 + (k + 1)x + kx²,

так как kx²  0, то тем более справедливо:

(1 + x) ^k+1  1 + (k + 1)x,

то есть неравенство Я.Бернулли справедливо для (k + 1) натурального числа, то справедливо для любого n.

Докажем справедливость формулы бинома Ньютона при помощи метода математической индукции.

1. Проверим справедливость формулы
   

при n = 0

(a + b)⁰ = 1;

n = 1

(a + b) ¹ = a + b;

n = 2

(a + b) ² = a² + 2ab + b²;

n = 3

(a + b) ³ = a³ + 3a²b + 3ab² + b³;

n = 4

(a + b) ⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴

n = 5

(a + b) ⁵ = a⁵ + 5a⁴b + 10a³b² + 10a²b³ + 5ab⁴ + b⁵

и так далее.

Коэффициенты каждого члена разложения называются биномиальными коэффициентами.

Нетрудно проверить, что любой коэффициент разложения может быть вычислен по формуле

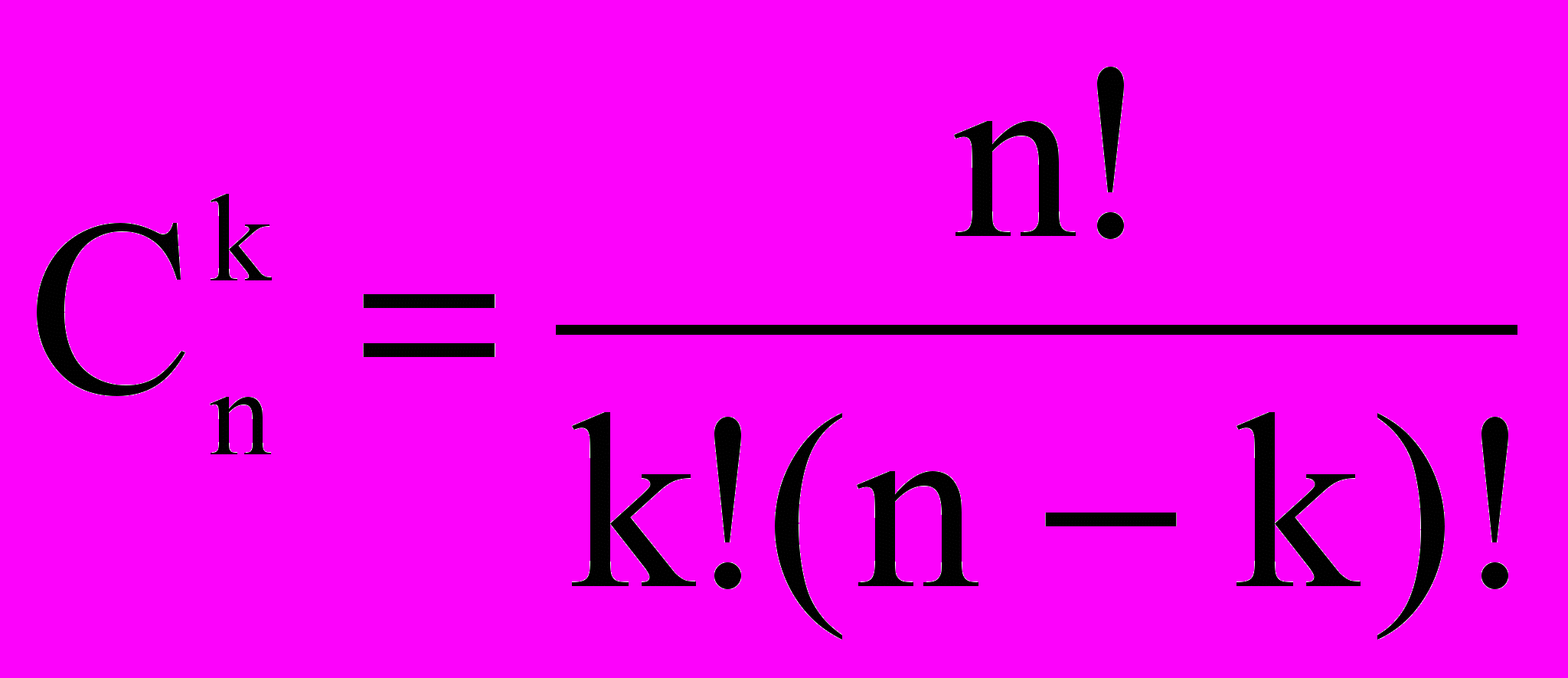(читается: С из «n» по «k»)

Значения биномиальных коэффициентов могут быть последовательно определены из так называемого треугольника Паскаля:

n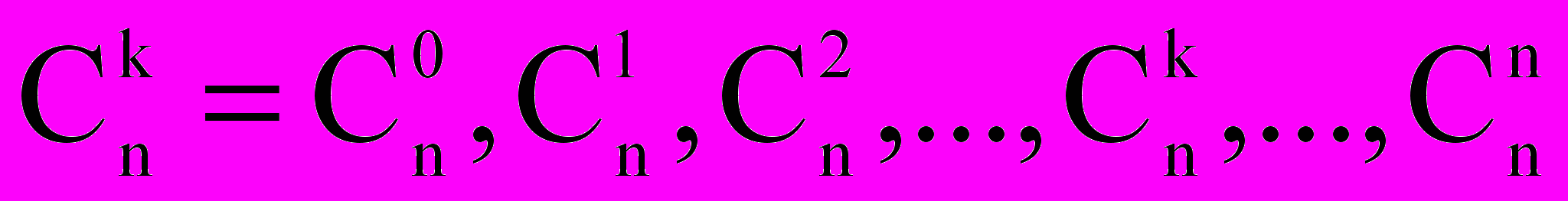
0											1
1									1			1
2								1		2			1
3							1		3			3		1
4						1		4			6		4		1
5				1			5		10			10		5		1
6			1		6			15		20			15		6		1
7		1		7			21		35			35		21		7		1
…

Каждый коэффициент образуется путем сложения двух стоящих над ним (справа и слева). Крайние значения для любого n = 1, так как



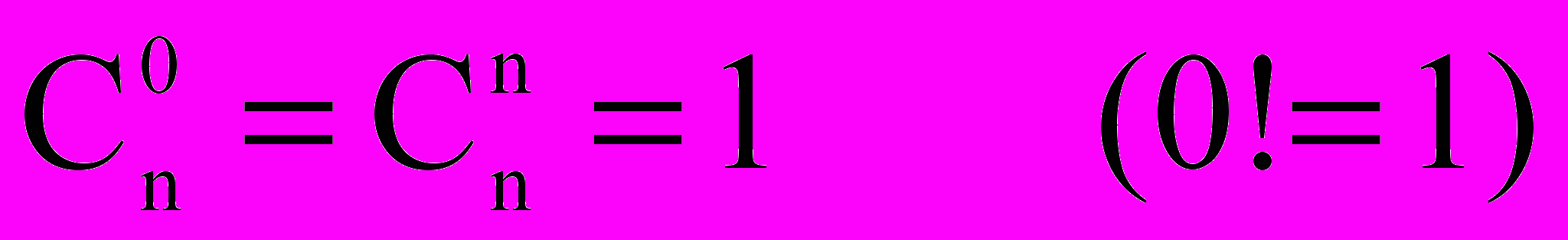
Видно, что биномиальные коэффициенты для любого n симметричны. Действительно, так как



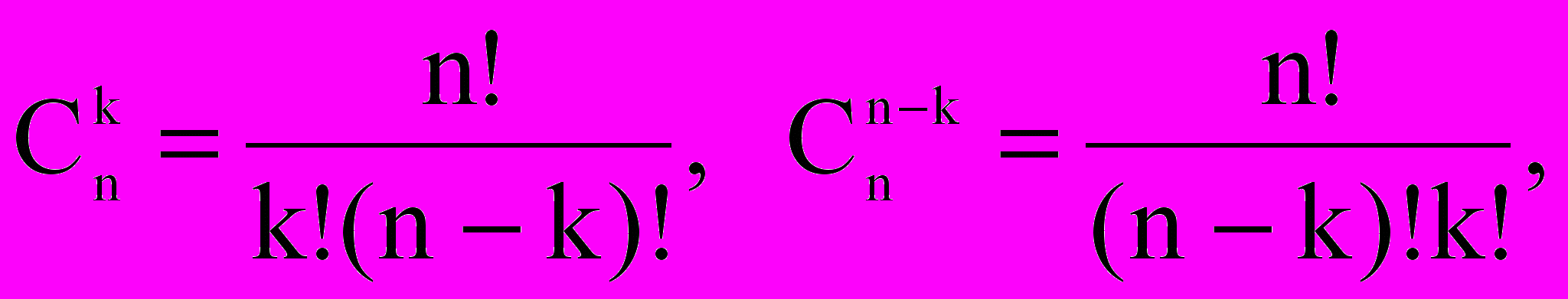
то

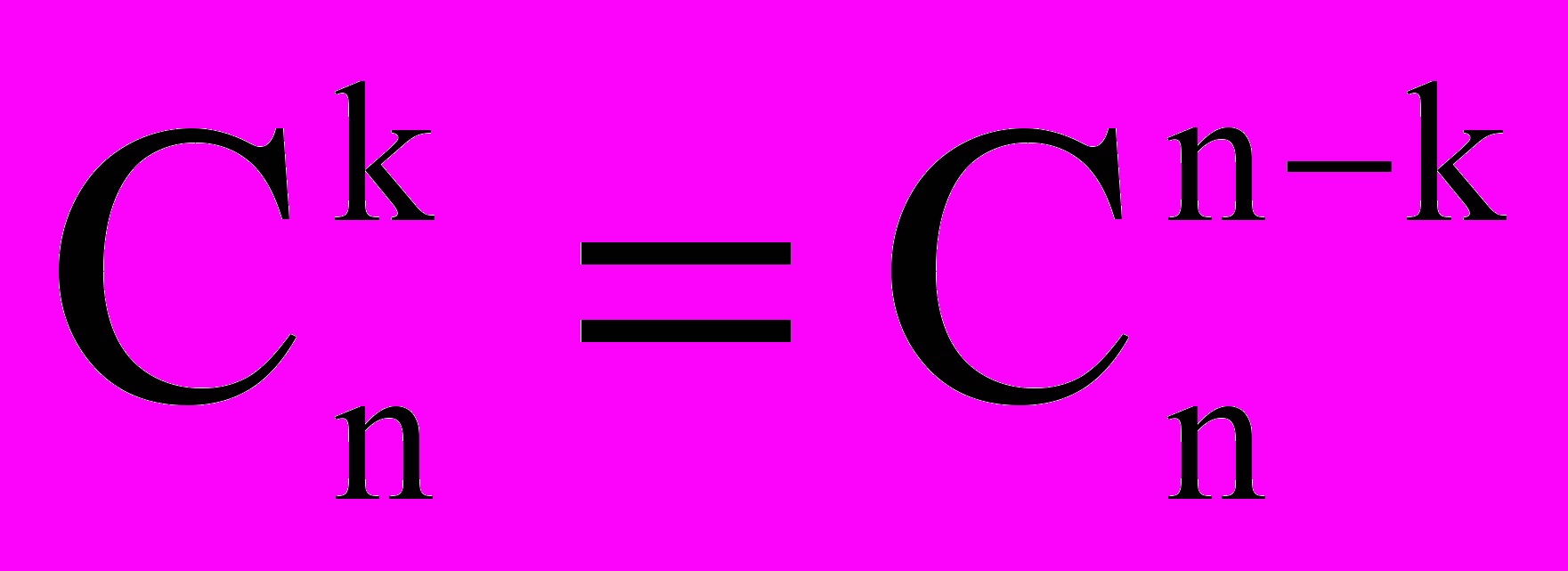
2. Предположим, что формула бинома верна для первых n членов натурального ряда, то есть
   

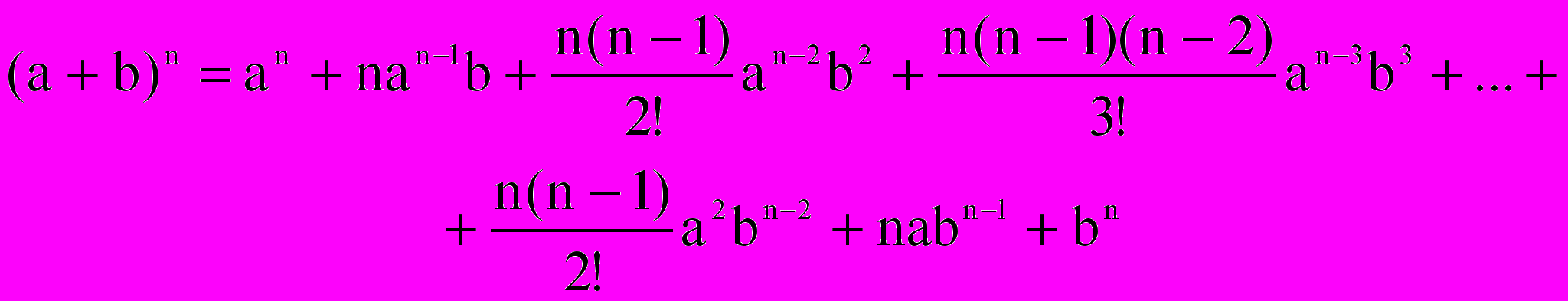
3. Докажем, что формула верна для (n + 1) натурального числа:
   

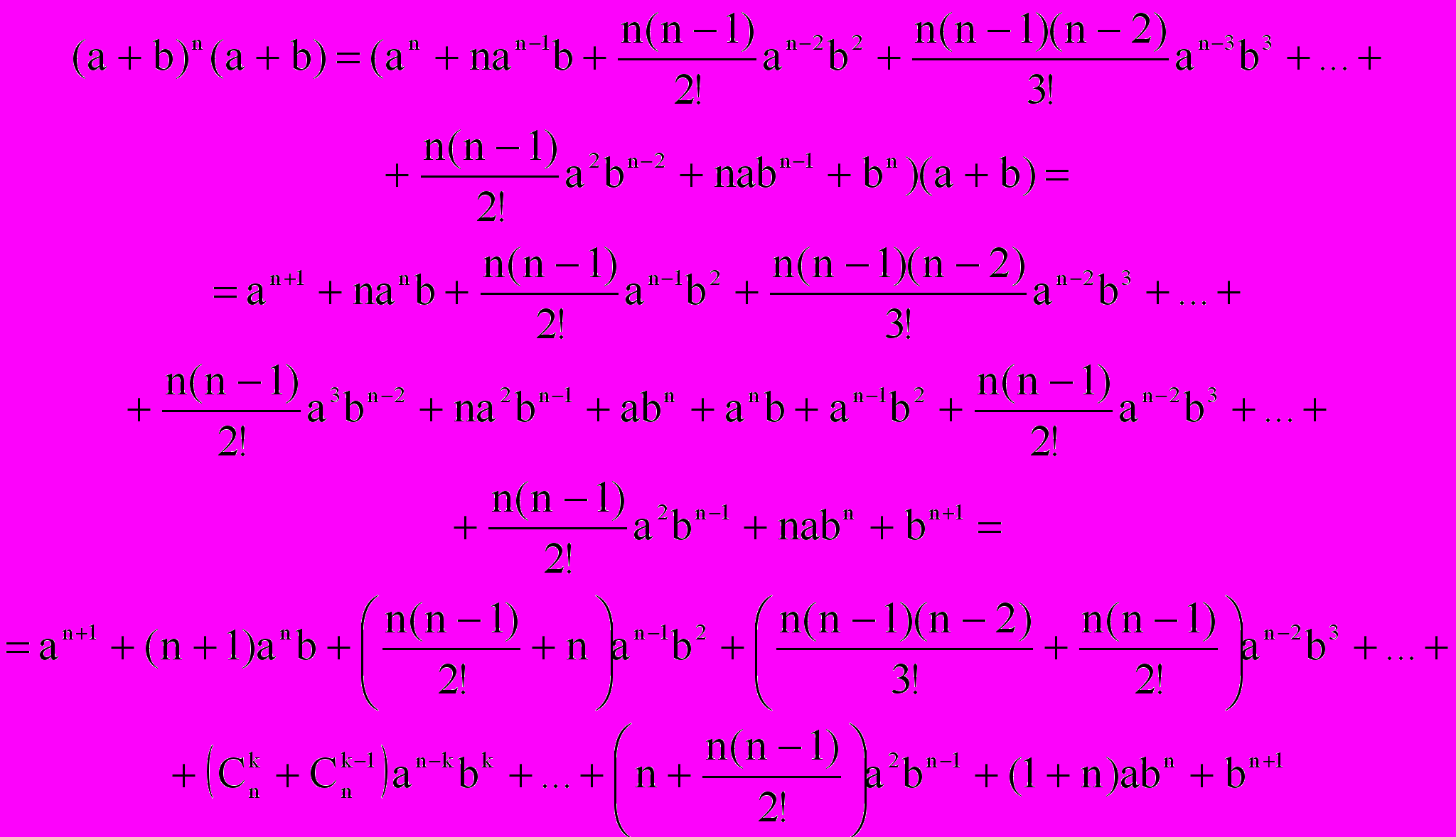
Структура полученной формулы совпадает со структурой бинома Ньютона, докажем, что коэффициенты полученного разложения представляют собой биномиальные коэффициенты для (n + 1) натурального числа.





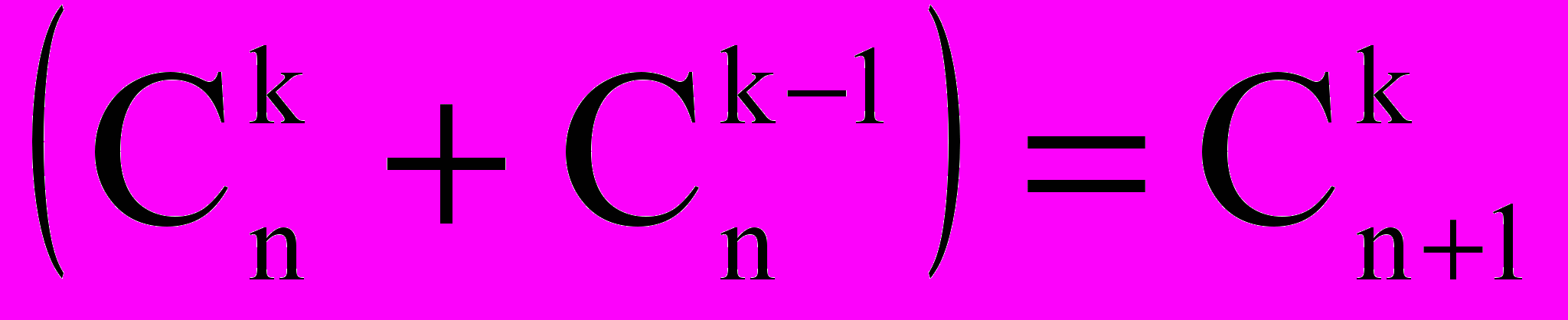
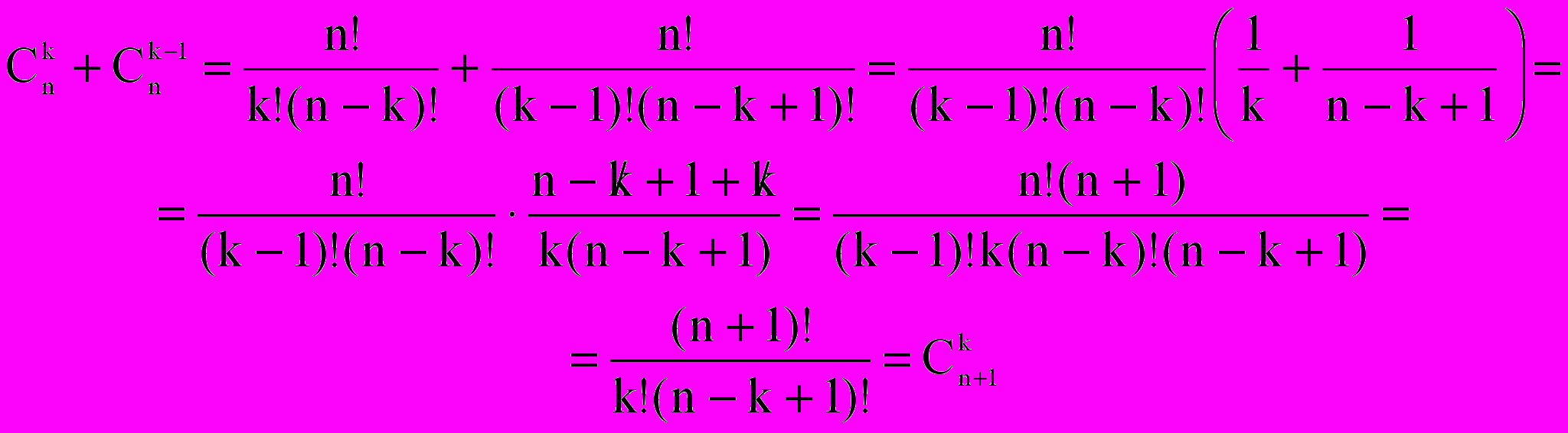
Таким образом, формула бинома Ньютона справедлива для любого n.

Бином Ньютона и биномиальные коэффициенты играют огромную роль во всех разделах высшей математики.

Так, например, в комбинаторике 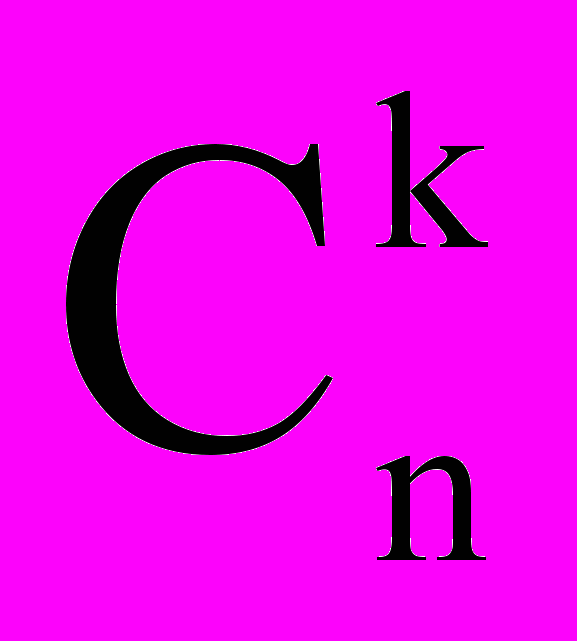показывают числами сочетаний (без повторений) групп по «k» элементов из множества «n» элементов.

Примеры.

1. Сколькими способами можно рассадить группу из 28 человек по двое за парту?
   

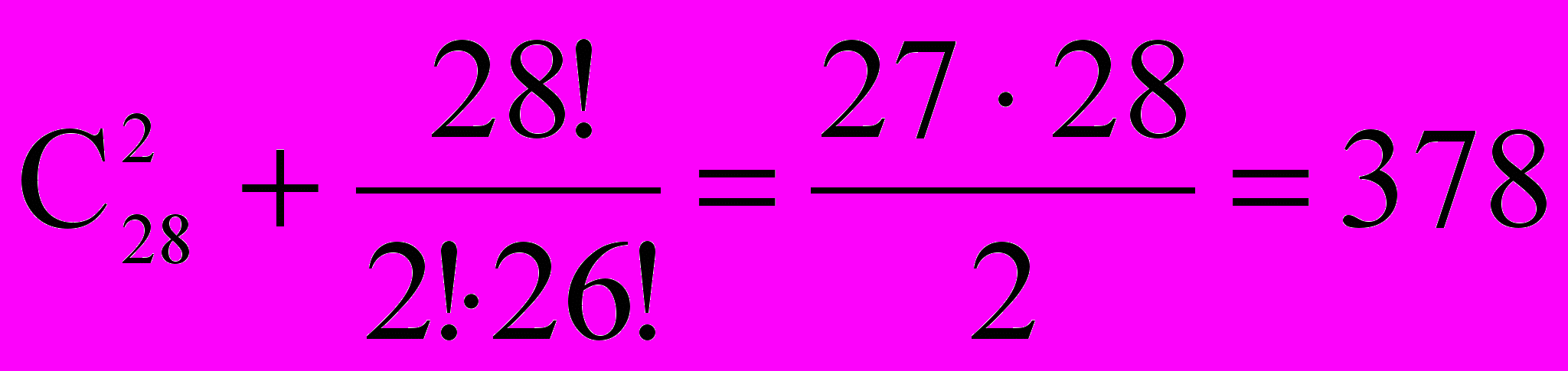
Всего 378 способов рассадить по двое группу из 28 человек.

2. Сколько миноров k–го порядка М_k содержится в k строках (или k столбцах) в определителе n–го порядка?
   

Очевидно, что всего таких миноров М_k .

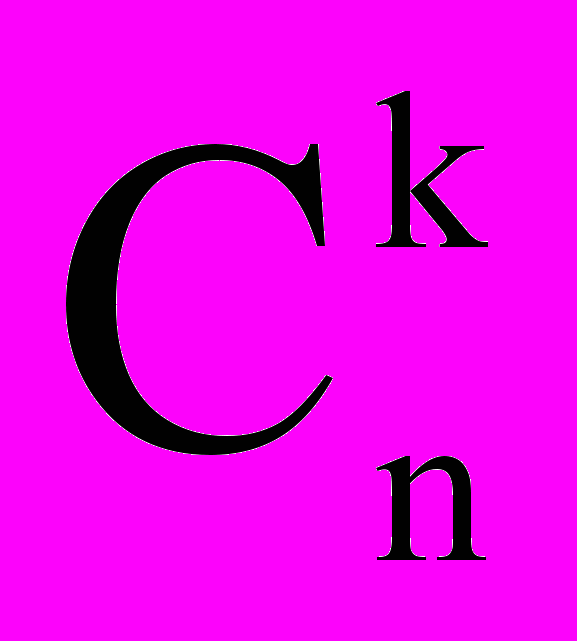Теорема Лапласа

Теорема. Определитель n–го порядка может быть разложен одновременно по k строкам (или k столбцам), при этом он равен алгебраической сумме произведений всех миноров k–го порядка М_k на их алгебраические дополнения А_k.

Определение минора k–го порядка было рассмотрено в лекции 9.

Минором k–го порядка М_k называется определитель k–го порядка, оставшийся после вычеркивания любых k строк и k столбцов.

При этом невычеркнутые (n–k) строк и (n–k) столбцов составляют определитель (n–k)–го порядка. Назовем его минором (n–k)–го порядка и обозначим М_n–k .

По отношению к М_k М_n–k будет являться дополняющим его минором, назовем М_n–k = М_k'. Таким образом, М_k – основной минор, М_k' – дополняющий его минор.

Замечание. Если бы мы вычеркивали (n–k) строк и (n–k) столбцов, то минор М_k' был бы основной, а невычеркнутый минор k–го порядка М_k был бы дополняющий его минор, то есть



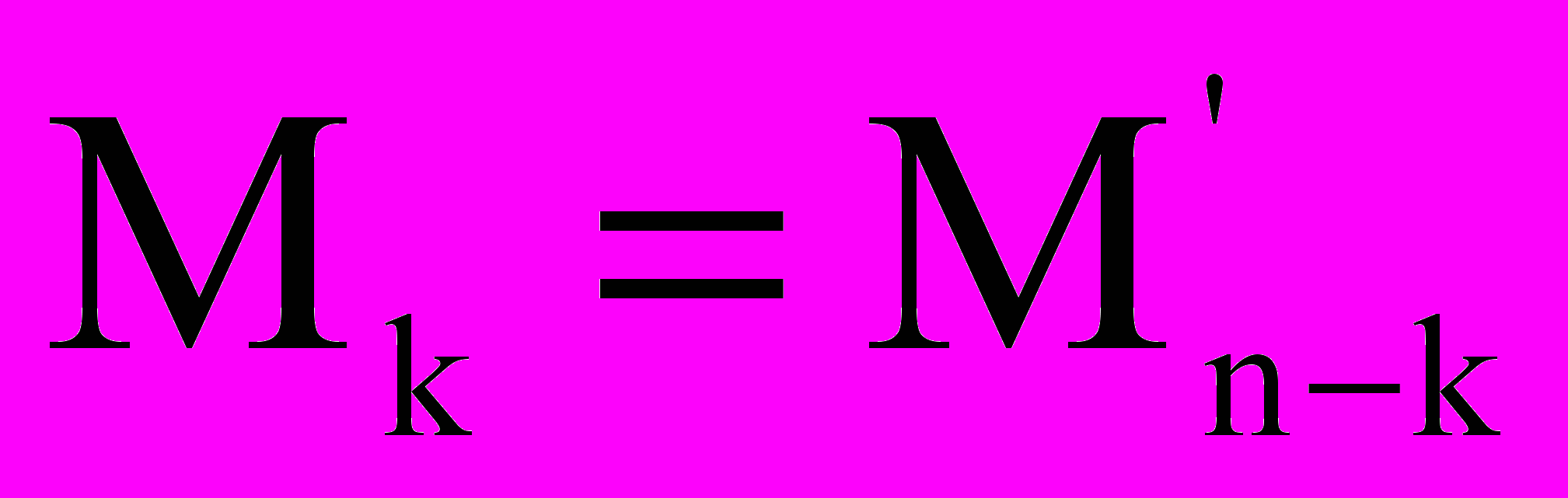
Алгебраическим дополнением минора k–го порядка М_k назовем число А_k, равное определителю дополняющего его минора М_k', взятому со знаком «плюс» или «минус»: «плюс», если сумма номеров вычеркнутых строк и столбцов четная, «минус» – нечетная.

Таким образом,

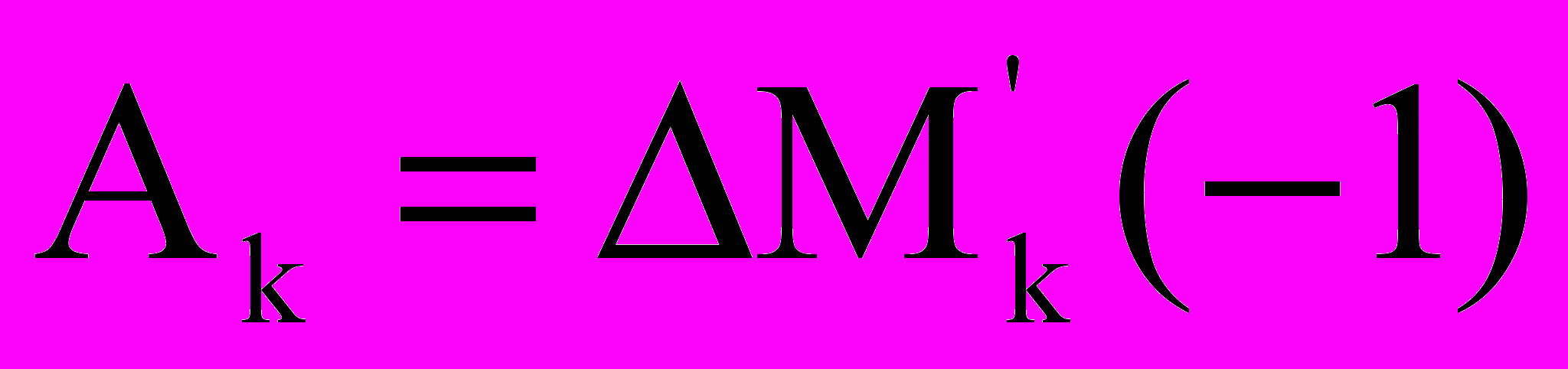^{[сумма номеров всех вычеркнутых строк и столбцов]}

Итак, определитель n–го порядка  по теореме Лапласа может быть разложен одновременно по k строкам (или k столбцам).

Замечание. Основная теорема о разложении может рассматриваться как частный случай теоремы Лапласа при k = 1.

Теорему Лапласа выгодно применять для вычисления определителей, содержащих симметрично расположенные нули.

Продемонстрируем применение теоремы Лапласа на примерах.

Примеры.

1. 
   

4 =	0	1	1	0
	– 1	2	2	1
	3	4	4	3
	0	2	3	0

Разложим этот определитель по 2–м строкам: первой и четвертой (т.е. вычеркнем 1–ю и 4–ю строки).

В вычеркнутых строках содержится С₄²= 6 миноров 2–го порядка М₂, но только один из этих миноров не равен нулю: он содержится в 1–й и 4–й строке и 2–м и 3–м столбце, остальные равны нулю из–за симметрично расположенных нулей. Тогда

4 =	1	1		– 1	1	(– 1)1+4+2+3 = – 6
	2	3		3	3

2. 
   

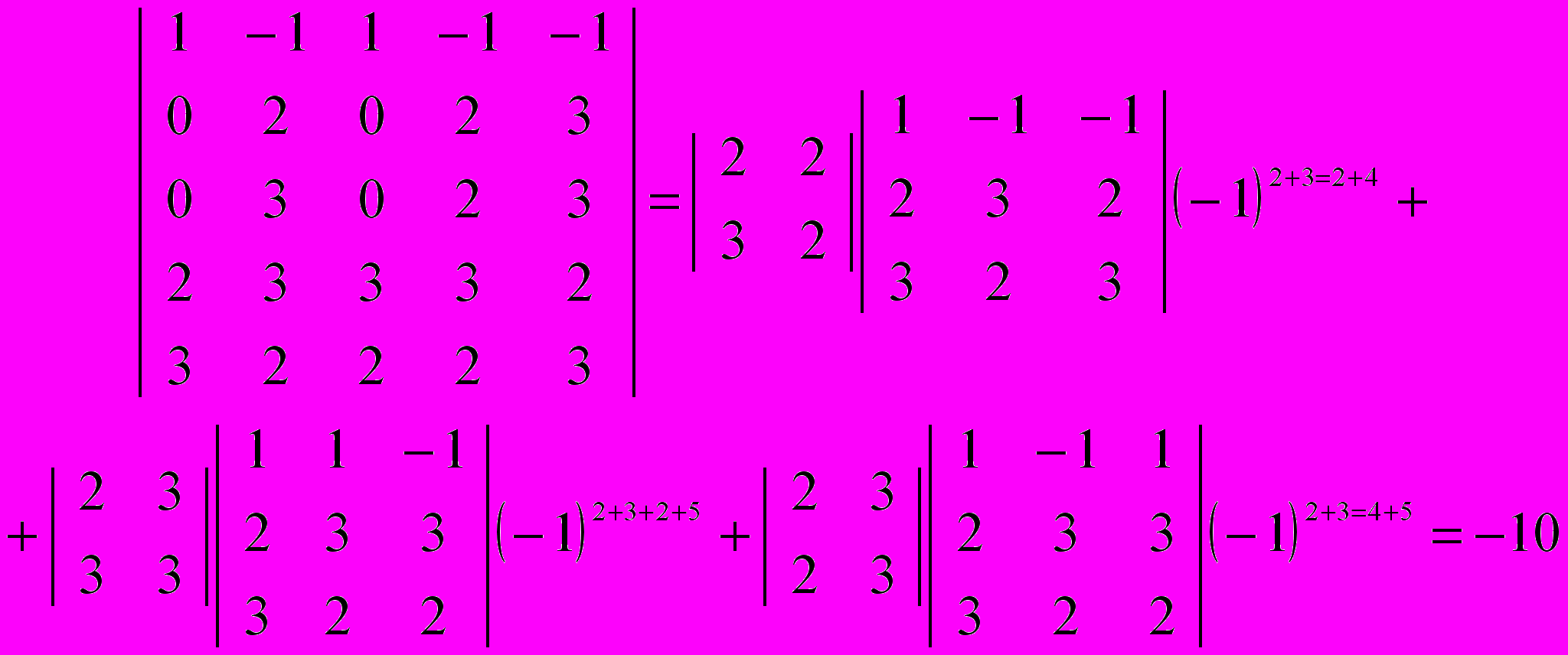
Список рекомендуемой литературы

1. Баврин И.И. Высшая математика: учебник для вузов / И.И.Баврин. – 6 е изд., стереотип. – М.: Академия, 2007.
   
2. Щипачев В.С. Курс высшей математики: учебник для вузов / В.С.Щипачев. – М.: Оникс 21 век, 2007.
   
3. Щипачев В.С. Задачник по высшей математике: учебное пособие для вузов / В.С.Щипачев. – 7 е изд., стереотип. – М.: Высшая школа, 2007.
   
4. Зуева Т.В. Линейная алгебра: учебное пособие / Т.В.Зуева. – СПб.: УМЦ Комитета по образованию, 2006.
   
5. Данко П.Е. Высшая математика в упражнениях и задачах в 2 частях: учебное пособие для вузов / П.Е.Данко, А.Г.Попов, Т.Я.Кожевникова. – М.: Оникс 21 век, 2006.