Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»
| Вид материала | Учебное пособие |
СодержаниеЗадача о пересечении2-х прямых на плоскости |
- Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
- Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
- Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
- Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
- Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
- Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
- Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
- Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
- Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
- Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.
Задача о пересечении
2-х прямых на плоскости
Простая задача о пересечении 2-х прямых на плоскости приводит к необходимости и обоснованности введения понятия определителя II порядка.
Пусть даны 2 прямые на плоскости:
Уравнение a1x + b1y= c1 – уравнение 1-й прямой
Уравнение a2x + b2y= c2 – уравнение 2-й прямой
Решим систему уравнений:
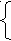a1x + b1y= c1 a2x + b2y= c2
Исключим неизвестное «y» из системы. Для этого правую и левую часть каждого уравнения умножим на «b2» и «b1» соответственно. Теперь, вычтем из 1-го уравнения 2-е уравнение. Получим:
(a1b2 – a2b1) x = c1b2 – c2b1
| x = | c1b2 – c2b1 | = | c  1 | b1 |
| c2 | b2 | |||
| a1b2 – a2b1 | a1 | b1 | ||
| a2 | b2 |
Видно, что удобно для вычисления x записать числитель и знаменатель дроби через определитель II порядка.
Аналогично, для вычисления «y» исключим неизвестное «x». Для этого умножим правую и левую части каждого уравнения на «a1» и «a2» соответственно и вычтем из 2-го уравнения 1-е уравнение. Получим:
(a1b2 – a2b1) y = a1c2 – a2c1
-
y =
a1c2 – a2c1
=
a1
c1
a2
b2
a1b2 – a2b1
a1
b1
a2
b2
Видно, что знаменатель дроби для вычисления «y» такой же, как и знаменатель дроби для вычисления «x», и он равен определителю II порядка, элементы которого –коэффициенты при неизвестных «x» и «y» в 1-м и 2-м уравнениях. Назовем его условно главным определителем Δ.
Определители II порядка, стоящие в числителях дробей получены из главного, но определитель для вычисления «x» - путем замены 1 столбца на столбец с1, с2, а «y» - путем замены 2 столбца на столбец с1, с2. Назовем эти определители добавочными при x и при y: Δ x и Δy
-
Δx=
c1
b1
Δy=
a1
c1
c2
b2
a2
c2
Т
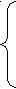аким образом, решение системы| x= | Δx |
| Δ | |
| y= | Δy |
| Δ |
Полученный результат, записанный через определители II порядка, облегчает и убыстряет решение данной задачи и систем линейных уравнений.