Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»
| Вид материала | Учебное пособие |
СодержаниеЛекция 3. Определители n-го порядка.Вычисление определителей |
- Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
- Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
- Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
- Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
- Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
- Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
- Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
- Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
- Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
- Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.
Лекция 3.
Определители n-го порядка.
Вычисление определителей
Определителем n-го порядка называется число Δ, соответствующее таблице элементов из n строк и n столбцов и равное алгебраической сумме произведений элементов, взятых по одному из каждой строки и каждого столбца.
| = | а11 | а12 | | а1n |
| a21 | a22 | | a2n | |
| - - - - - - - - - - - - - - - | ||||
| an1 | an2 | | ann | |
Совершенно очевидно, что, пользуясь определением, трудно перебрать все возможные произведения элементов по одному из каждой строки и столбца, кроме того, неизвестно, как выбирать знаки произведений, входящих в алгебраическую сумму.
Теорема о разложении справедлива для вычисления определителя любого порядка: определитель равен алгебраической сумме произведений любой строки (или столбца) на их алгебраические дополнения.
Минор Мij элемента аij в определителе n-го порядка – это определитель (n-1)-го порядка, который остался после вычеркивания i-строки и j-столбца.
Алгебраическое дополнение Аij элемента аij – это число, соответствующее определителю Мij, взятому со знаком «+», если сумма (i+j) – четная, и «-» , если (i+j) – нечетная.
Таким образом, определитель n-го порядка может быть разложен на сумму n определителей (n-1)-го порядка, каждый из которых в свою очередь может быть разложен на сумму (n-1) определителя (n-2)-го порядка и т.д.
Этим способом может быть вычислен определитель любого порядка, хотя это и не самый радикальный метод.
Если же в определителе n-го порядка есть столбец (или строка), состоящий (состоящая) из нулевых элементов, кроме одного, то, раскладывая определитель именно по этому столбцу (или строке), можно понизить определитель на один порядок.
Н
 апример,
апример,| a  11 11 | 0 | 0 | | 0 | | | | | |
| a21 | a22 | a23 | | a2n | = а11 | a22 | a23 | | a2n |
| | | | | | | | | | |
| an1 | an2 | an3 | | ann | | an2 | an3 | | ann |
Здесь видно, что, раскладывая по элементам 1-й строки, только элемент а11 в произведении со своим алгебраическим дополнением дает отличное от нуля произведение.
Все свойства определителей, сформулированные и доказанные в лекции 2, справедливы и для определителей n-ного порядка. Используя эти свойства, можно делать линейные преобразования над строками и столбцами, добиваясь обнуления элементов строк (или столбцов) кроме одного (условно назовем его «главным элементом»).
Н

 апример,
апример,| 1 | 2 | 4 | 6 | = 2 3 | 1 | 1 | 4 | 2 |
| - 2 | 4 | 7 | - 9 | - 2 | 2 | 7 | - 3 | |
| 2 | - 6 | - 5 | 3 | 2 | - 3 | - 5 | 1 | |
| 3 | 8 | 4 | 6 | 3 | 4 | 4 | 2 |
(из 2-го столбца вынесли общий множитель 2, из 4-го столбца – 3)
Любой из элементов этого определителя может быть условно назван «главным элементом». Лучше в качестве «главного элемента» выбирать «1» либо «- 1», чтобы избежать дробных вычислений.
В
 качестве главного элемента выберем, например, «1», как элемент а11
качестве главного элемента выберем, например, «1», как элемент а11| 1    | 1 | 44 | 22 | = | 1 | 0 | 0 | 0 | = | | | |
| - 2 | 2 | 7-8 | - 3-4 | - 2 | 4 | 15 | 1 | 4 | 15 | 1 | ||
| 2 | - 3 | -58 | 14 | 2 | - 5 | -13 | - 3 | - 5 | -13 | - 3 | ||
| 3 | 4 | 412 | 26 | 3 | 1 | - 8 | - 4 | 1 | - 8 | - 4 |
Используя свойство 6, можно за счет а11 обнулить элементы строки, в которой стоит «главный элемент» (или столбца, в котором стоит «главный элемент»), кроме этого элемента. Предположим, что необходимо обнулить элементы строки. Тогда столбец, в котором стоит «главный элемент», назовем условно главным столбцом. То есть 1-й столбец – главный.
Подбирая коэффициенты и складывая 1-й столбец (или вычитая, если коэффициент отрицательный) по очереди со 2-м, 3-м, 4-м, можно добиться, что элементы 1-й строки будут равны 0, кроме а11. Так, чтобы обнулить а12, необходимо 1-й столбец вычесть из 2-го; чтобы обнулить а13, необходимо 1-й столбец умножить на 4 и вычесть из 3-го; чтобы обнулить а14, необходимо элементы 1-го столбца умножить на 2 и вычесть из 4-го. Теперь все элементы 1-й строки, кроме главного, равны «0».
Раскладывая определитель по 1-й строке, понизим его порядок с 4-го до 3-го.
Определитель 3-го порядка также может быть понижен до 2-го, который легко вычисляется.


| 4   | 15 | 1 | = | 4 | 15 | 1 | = |
| - 512 | -1345 | -33 | 7 | 32 | 0 | ||
| 116 | -860 | -44 | 17 | 52 | 0 | ||
| | | ||||||
| = | 7 | 8 | = 4 | 7 | 8 | = | |
| 17 | 52 | 17 | 13 | | |||
| | | ||||||
| = 4(91 – 136) = - 180 | | ||||||
Так как в исходном определителе 4-го порядка были вынесены множители 2 и 3, то необходимо для окончательного ответа сделать умножение
2 3(-180) = - 1080.
В качестве «главного элемента» в самом начале вычисления можно было выбрать любой другой элемент. На результат выбор элемента не влияет. Например,


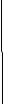
| 2   3 3 | 1 | 1 | 4 | 2 | = 6 | 1 | 1 | 4 | 2 | = | ||||||
| -22 | 22 | 78 | -34 | -4 | 0 | -1 | -7 | |||||||||
| 23 | -33 | -512 | 16 | 5 | 0 | 7 | 7 | |||||||||
| 34 | 44 | 416 | 28 | -1 | 0 | -12 | -6 | |||||||||
  | ||||||||||||||||
| =   -6 -6 | -4 | -1 | -7 | =-6 | 4 | 1 | 7 | =-6 | 4 | 1 | 7 | = | ||||
| 5 | 7 | 7 | 528 | 77 | 749 | -23 | 0 | -42 | ||||||||
| -1 | -12 | -6 | 148 | 1212 | 684 | -47 | 0 | -78 | ||||||||
| | ||||||||||||||||
| = 6 | -23 | -42 | = 6 | 23 | 42 | = | | | | | | |||||
| -47 | -78 | 47 | 78 | | | | | | ||||||||
| | ||||||||||||||||
| = 6(1794 – 1974) = 6( -180) = - 1080 | ||||||||||||||||
Очень часто в определителях нет строк (столбцов) с кратными элементами, нет элементов, которые по абсолютной величине равны «1», т.е. представляет затруднение выбор «главного элемента». Существует много способов искусственно получить «единичные» элементы, за счет которых можно обнулять элементы строк (столбцов), избегая дробных вычислений. Эти способы часто индивидуальны, зависят от опыта и интеллекта вычисляющего. Однако существуют и некоторые стандартные приемы.
Например,
| 5 | 6 | 6 | 6 |
| 6 | 5 | 4 | 3 |
| 6 | 4 | 5 | 3 |
| 6 | 3 | 4 | 5 |
В данном определителе нет единиц. Все элементы не кратные. Можно этот определитель разложить по строке (столбцу) на сумму 4х определителей 3-го порядка. Однако, если а11=5 представить, как (6 - 1), а все «6»-ки в 1-м столбце (или в 1-й строке), как (6 - 0), то
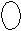


| 6     -1 -1 | 6 | 6 | 6 | = | 6 | 6 | 6 | 6 | - | 1 | 6 | 6 | 6 | = | 6 | 6 | 6 | 6 | - | |||
| 6-0 | 5 | 4 | 3 | 6 | 5 | 4 | 3 | 0 | 5 | 4 | 3 | 0 | -1 | -2 | -3 | |||||||
| 6-0 | 4 | 5 | 3 | 6 | 4 | 5 | 3 | 0 | 4 | 5 | 3 | 0 | -2 | -1 | -3 | |||||||
| 6-0 | 3 | 4 | 5 | 6 | 3 | 4 | 5 | 0 | 3 | 4 | 5 | 0 | -3 | -2 | -1 | |||||||
| | ||||||||||||||||||||||
| - | 5 | 4 | 3 | = -6 | 1 | 2 | 3 | - | 5 | 4 | 3 | = | | | | | | | ||||
| 4 | 5 | 3 | 2 | 1 | 3 | 4 | 5 | 3 | | | | | | | ||||||||
| 3 | 4 | 5 | 3 | 2 | 1 | 3 | 4 | 5 | | | | | | | ||||||||
| | ||||||||||||||||||||||
| = - 6 12 – 24 = - 24(3 + 1) = - 24 4= - 96 | ||||||||||||||||||||||
Здесь по свойству 4 определитель разложен на сумму двух определителей 4-го порядка, каждый из которых понижен до 3-го. Определители III порядка могут быть вычислены по правилу Саррюса, либо по теореме о разложении с использованием (или не использованием) линейных преобразований над строками (столбцами).
