Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»
| Вид материала | Учебное пособие |
СодержаниеПриложение 2 Некоторые сведения из теории множеств.Комбинаторика.Перестановки и подстановки Определитель n-го порядка |
- Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
- Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
- Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
- Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
- Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
- Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
- Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
- Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
- Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
- Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.
Приложение 2
Некоторые сведения из теории множеств.
Комбинаторика.
Перестановки и подстановки
Рассмотрим упорядоченное множество из n элементов. Пусть это будет множество натуральных чисел
1, 2, 3, …, n.
Установленный в конечном множестве порядок называют перестановкой его элементов. Число перестановок конечного множества элементов зависит только от числа элементов. Для множества из n элементов число перестановок обозначают Рn
Рn = 1 2 3 … (n – 1) n = n! (читается n-факториал)
Рассмотрим некоторую перестановку множества из n элементов
(… i … j …).
Числа i и j называются инверсией, если i в перестановке стоит раньше, чем j, но i j.
Если число инверсий в перестановке четное, то и перестановка называется четной, если нечетное число инверсий, то и перестановка называется нечетной.
Например, n = 5, тогда (1, 2, 3, 4, 5) – одна из возможных 5! перестановок этого множества. Очевидно, что в этой перестановке нуль инверсий.
Рассмотрим какую-нибудь другую перестановку множества из пяти элементов. Например,
(3, 5, 2, 1, 4)
Перечислим пары чисел, которые составляют инверсии
3 и 2, 3 и 1, 5 и 2, 5 и 1, 5 и 4, 2 и 1.
Таким образом, в этой перестановке число инверсий – 6. Перестановка – четная.
Очевидно, что максимальное число инверсий будет соответствовать перестановке, где все элементы взяты в обратном порядке:
(5, 4, 3, 2, 1)
Для перестановки множества из 5 элементов максимальное число инверсий 10.
Часто возникает вопрос: чему равно максимальное число инверсий в перестановке множества из n элементов?
Очевидно, что минимальное число инверсий 0 соответствует прямой перестановке (1, 2, 3, …, n), а максимальное число соответствует обратной перестановке (n, n – 1, n – 2, …, 3, 2, 1).
С элементом n составляют инверсии остальные (n – 1)-элементы, с
(n – 1) – остальные (n – 2)-элементы, стоящие за ним справа, и т.д.
Тогда
[max число инверсий] = (n – 1) + (n + 2) + … + 2 + 1 = Sn–1,
где Sn–1 – сумма (n – 1)-числа натурального ряда, которую можно вычислить как сумму убывающей арифметической прогрессии, начинающейся с (n – 1) с разностью прогрессии (- 1):
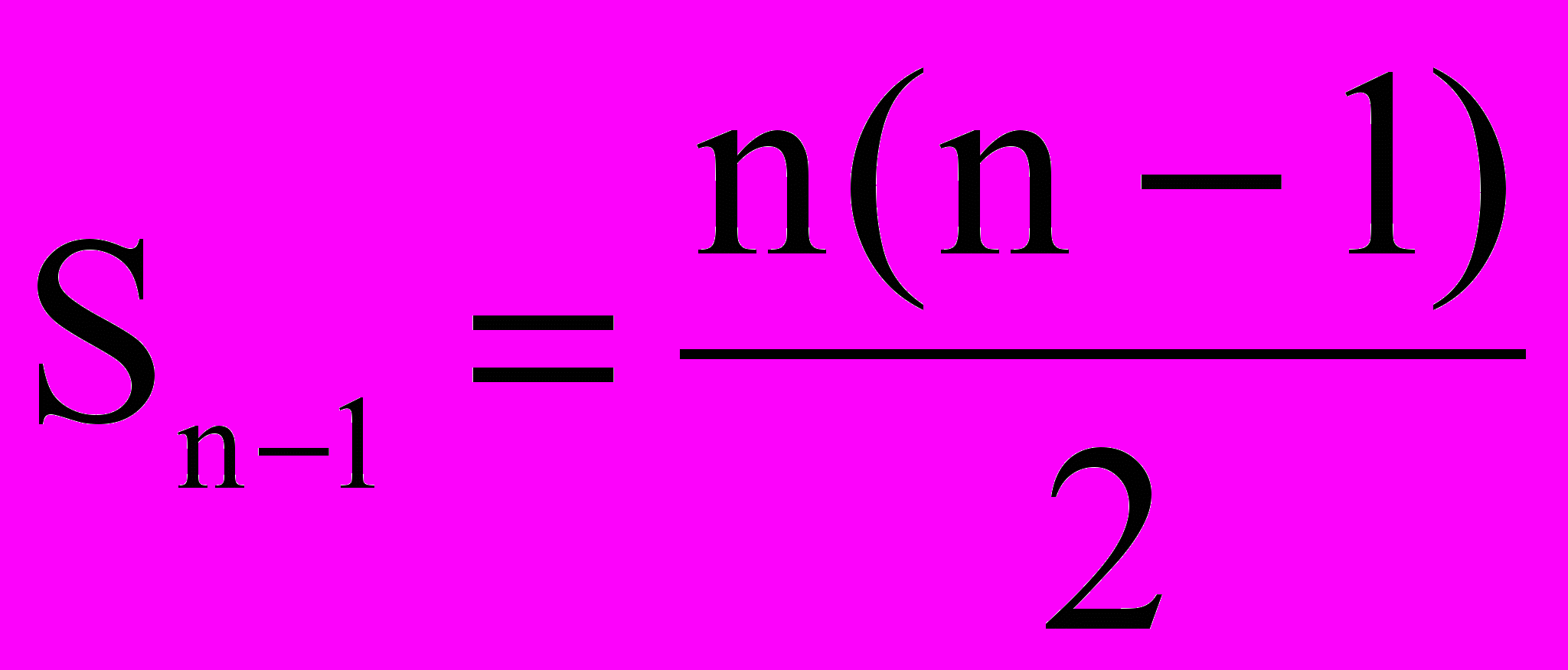 |
Таким образом, число инверсий изменяется от 0 до
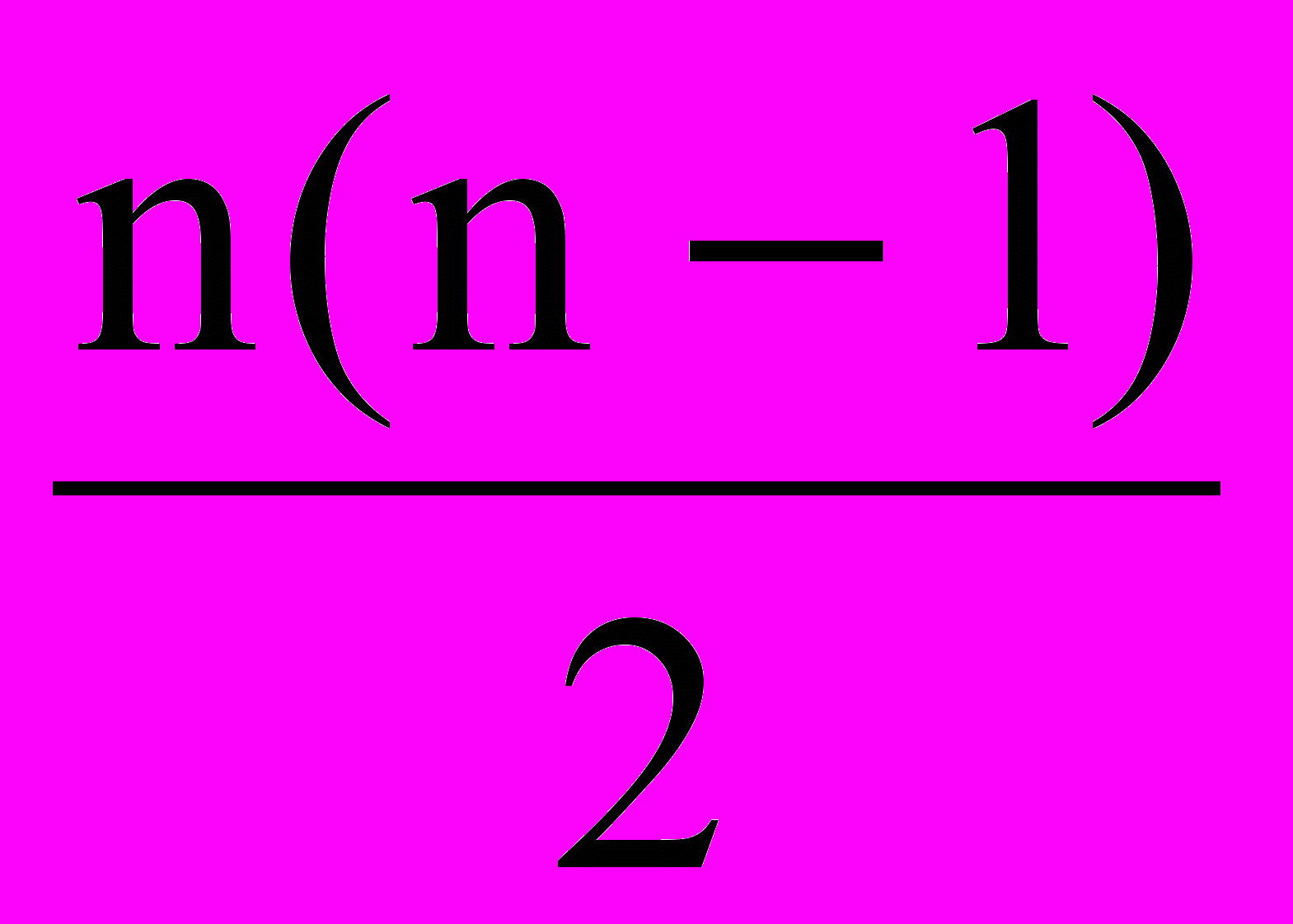 .
.Количество четных и нечетных перестановок очевидно одинаково.
Если написать одну перестановку под другой, получим подстановку из n элементов. Такая запись выглядит следующим образом:
 1 2 … n
1 2 … n1 2 … n , где
(1 2 … n) – одна из (n!) перестановок множества.
Часто говорят, «1» переходит в «1», «2» - в «2», …, «n» - в n.
Очевидно, что в подстановке из n элементов можно перебрать n! различных подстановок.
По общему числу инверсий подстановки разделяются на четные и нечетные. Например,
5 4 3 2 1 | В верхней перестановке 0 инверсий, в нижней – 10. Общее число инверсий – 10, подстановка – четная. |
 1 3 4 5 1 3 4 5 | Эта запись не является подстановкой, т.к. нижняя перестановка не является перестановкой множества из 5 элементов |
Определитель n-го порядка
На примере определителя III порядка рассмотрим определитель n-го порядка как алгебраическую сумму произведений элементов, взятых по одному из каждой строки и каждого столбца с точки зрения комбинаторских задач конечного множества.
Итак,
| 33 = | а11 | а12 | а13 | =а11а22а33 - а13а22а31 - а12а21а33 + + а12а31а23 + а13а21а32 - а11а23а32 |
| а21 | а22 | а23 | ||
| а31 | а32 | а33 |
В каждое произведение взят один элемент из каждой строки и каждого столбца, то есть в определителе III порядка элементов, входящих в произведение, три. Очевидно, что в определителе n-го порядка элементов, входящих в произведение, n.
Таких произведений из 3-х элементов (из n элементов) можно перебрать столько, сколько существует различных подстановок, соответствующих индексам элементов, входящих в произведение.
Действительно, в определителе III порядка произведений, входящих в алгебраическую сумму, 6, то есть (3!). Очевидно, что в определителе n-го порядка произведений – n!.
Из (n!) произведений с «плюсом» и с «минусом» – одинаковое количество, причем знак произведения соответствует четности (нечетности) подстановки индексов элементов, участвующих в произведении: если подстановка четная, то знак «плюс», если нечетная, то «минус».
В
 определителе III порядка каждому произведению соответствует подстановка индексов:
определителе III порядка каждому произведению соответствует подстановка индексов:| а11а22а33 | | 1 | 2 | 3 | , [число инверсий] = 0; | |
| |  1 1 | 2 | 3 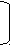 | |||
| - а13а22а31 | | 1 | 2 | 3 | , [число инверсий] = 3; | |
| | 3 | 2 | 1 | |||
| - 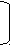 а12а21а33 а12а21а33 | 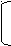 | 1 | 2 | 3 | , [число инверсий] = 1; | |
| | 2 | 1 | 3 | |||
| а12а31а23 |  | 1 | 3 | 2  | , [число инверсий] = 2; | |
| | 2 | 1 | 3 | |||
| а13а21а32 | 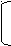 | 1 | 2 | 3 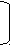 | , [число инверсий] = 2; | |
| | 3 | 1 | 2 | |||
| - 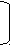 а11а23а32 а11а23а32 | 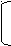 | 1 | 2 | 3 | , [число инверсий] = 1. | |
| | 1 | 3 | 2 | |||
Видно, что знак произведения соответствует четности подстановки индексов.
С
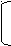 учетом данного подхода к понятию определителя n-го порядка отметим, что произведение элементов главной диагонали входит в алгебраическую сумму произведений со знаком «плюс» для любого n, так как индексы элементов, участвующие в произведении, составляют прямую подстановку.
учетом данного подхода к понятию определителя n-го порядка отметим, что произведение элементов главной диагонали входит в алгебраическую сумму произведений со знаком «плюс» для любого n, так как индексы элементов, участвующие в произведении, составляют прямую подстановку.| 1  | 2 | 3 | … | n | , [число инверсий] = 0. |
| 1 | 2 | 3 | … | n |
Произведению элементов побочной диагонали соответствует обратная подстановка
| 1   | 2 | 3 | … | n - 1 | n | , [число инверсий] = 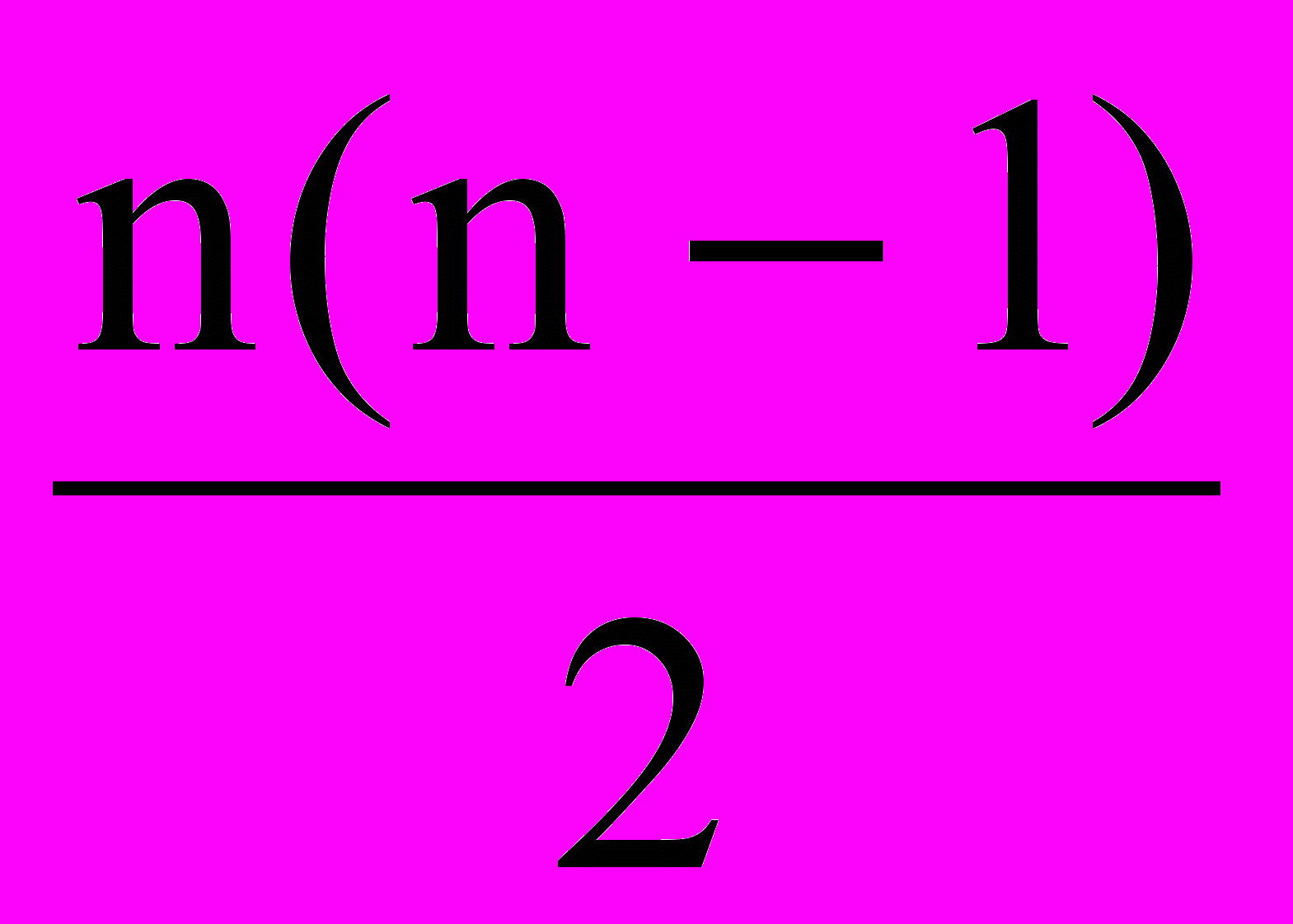 , , |
| n | n – 1 | n - 2 | … | 2 | 1 |
четность зависит от n, то есть знак произведения зависит от порядка определителя. Так, в определителе II и III порядков – «минус», в определителе IV порядка – «плюс» и так далее.

 2 3 4 5
2 3 4 5