Учебное пособие Санкт-Петербург 2007 Составила: Зуева Т. В. Ст методист: Регель Н. И. Пособие предназначено для изучения соответствующих разделов дисциплин «Математика» и«Элементы высшей математики»

Вид материала

Учебное пособие

Содержание Матричные уравнения

Подобный материал:

• Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Учебное пособие Санкт-Петербург 2007 удк алексеева С. Ф., Большаков В. И. Информационные, 1372.56kb.
• Учебное пособие санкт-петербург 2005 удк 339. 9 (075. 80) Ббк, 703.64kb.
• Учебное пособие Нижний Новгород 2007 Балонова М. Г. Искусство и его роль в жизни общества:, 627.43kb.
• Учебное пособие санкт-петербург 2 004 удк 669. 2/8; 669. 4 (075. 80) Ббк 34., 990.55kb.
• Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
• Н. В. Кацерикова ресторанное дело учебное пособие, 1607.02kb.
• Учебное пособие для студентов заочной формы обучения Санкт-Петербург, 1247.83kb.
• Предлагаемое учебное пособие предназначено для студентов, аспирантов и преподавателей, 2052.38kb.

Матричные уравнения

Рассмотрим систему линейных уравнений n-го порядка

а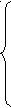₁₁x₁ + a₁₂x₂ + a₁₃x₃ + … + a_1nx_n = b₁

а₂₁x₁ + a₂₂x₂ + a₂₃x₃ + … + a_2nx_n = b₂ (1)

а₃₁x₁ + a₃₂x₂ + a₃₃x₃ + … + a_3nx_n = b<sub>3

…………………………………………………………</sub>

а_n1x₁ + a_n2x₂ + a_n3x₃ + … + a_nnx_n = b_n

Главный определитель системы – определитель квадратной матрицы А, составленный из коэффициентов при неизвестных

А=	а11	а12	…	а1n
	a21	a22	…	a2n
	- - - - - - - - - - - - - - - - - - - -
	an1	an2	…	ann

Неизвестные (х₁, х₂, ..., х_n) представим как матрицу – столбец

Х=	х1
	х2
	...
	хn

Правые части уравнений представим как матрицу – столбец свободных членов

В=	b1
	b2
	...
	bn

Тогда систему (1) можно записать в матричном виде (2)

АХ = В (2)

(2) представляет собой матричное уравнение. Если правую и левую часть этого уравнения умножить на А^-1, которая существует в случае А0 (кстати говоря, по правилу Крамера система совместна в случае А0), тогда получим

А^-1АХ = А^-1В,

т.к. А^-1А = Е, а ЕХ = Х, то

Х = А^-1В (3)

Сопоставим решение (3) в матричном виде с правилом Крамера

А^-1= (1/) Ã

Х=(1/) ÃВ

ÃВ=	А11	А21	: : : :	Аn1	b1	=
	А12	А22		Аn2	b2
	:	:		:	:
	А1n	А2n		Аnn	bn

=	A11b1+A21b2+...+An1bn		=		Δх 1
	A12b1+A22b2+...+An2bn				Δх 2
	.....................................				:
	A1nb1+A2nb2+...+Annbn				Δх n
Δх = 1		A11b1+A21b2+...+An1bn		=	b1	а12	: : : :	а1n
					b2	a22		a2n
					:	:		:
					bn	an2		ann

Δх = 2	A11b1+A21b2+...+An1bn =	а11	b1	: : : :	а1n
		a21	b2		a2n
		:	:		:
		an1	bn		ann

и т.д.

Δх = n	A1nb1+A2nb2+...+Annbn =	а11	а12	: : : :	b1
		a21	a22		b2
		:	:		:
		an1	an2		bn

Тогда

Х=	Δх / 1	, что подтверждает правило Крамера
	Δх / 2
	:
	Δх / n

В общем случае, в матричном уравнении АХ=В Х, В могут быть не только матрицей–столбцом, а матрицей такого размера, что АХ существует и равно В.

Тогда

Х = А^-1В

Матричное уравнение ХА = В решается аналогично, только

ХАА^-1 = ВА^-1, АА^-1=Е, ХЕ = Х,

Тогда

Х = ВА^-1

Матричные уравнения решаются сначала в матричном виде, а затем делаются обращения нужных матриц и далее необходимые действия.

Пример.

АХВ + D = C

AXB = C – D

(A^-1A)X(BB^-1) = A^-1(C – D)B^-1

X = A^-1(C – D)B^-1

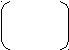
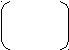
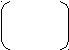
Пусть

А=	2	3	, В=	3	4	, С=	1	2	, D=	0	1
	-4	5		-4	3		2	1		1	0

A-1=(1/A)Ã= 1/22	5	- 3
	4	2

B-1=(1/B)B = 1/25				3		- 4
				4		3
C – D=	1	2	-		0		1		=	1	1
	2	1			1		0			1	1

X=1/221/25	5	-3	1	1	3	-4	=1/550	2	2	3	-4	=
	4	2	1	1	4	3		6	6	4	3

=1/550	14	-2	=1/275	7	-1
	42	-6		21	-3

Проверка

АХВ + D = C

AXB = 1/275						2		3	7		-1			3		4		=
						-4		5	21		-3			-4		3
= 1/275			77		-11			3		4		=1/25				25			25		=	1	1
			77		-11			-4		3						25			25			1	1
AXB+D=				1		1	+		0		1		=		1		2			, где
				1		1			1		0				2		1
1	2	=C Уравнение решено верно.
2	1