Пошаговое приближение распределения стоимости покупки к нормальному закону распределения
| Вид материала | Закон |
- Лабораторная работа 1-08 экспериментальное изучение гауссовского закона распределения, 108.63kb.
- Дискретные случайные величины Ряд распределения, 29.73kb.
- Природа каналов распределения товаров. Их структура и управление, 20.88kb.
- Лабораторная работа №2 Тема: Формирование выборки случайных чисел, распределенных, 151.75kb.
- Функция распределения. Плотность распределения. Основные параметры непрерывных случайных, 7.05kb.
- Законом распределения, 13.27kb.
- Методы и каналы распределения товаров, 82.28kb.
- Лекция 10. Управление системой распределения >10. Управление системой распределения, 258.27kb.
- Задача оптимизации расположения распределительного центра на обслуживаемой территории, 872.4kb.
- Секция №1 Модераторы: В. Стрельченок, Е. Толстая, И. Ратанова, 183.54kb.
Ход решения
(Рекомендуется использовать пакет Excel). Беря исходное значение К=1, вычисляем значения p(x) на указанном отрезке с шагом 0,1. Вычисляем площадь под этой кривой методом прямоугольников (основание каждого прямоугольника равно 0,1). Всего таких прямоугольников будет (примерно) (3,016 + 12,042)/0,1 = 151. <Для сверки: эта площадь равна 6,18; см. рис. 3>
Так как площадь под кривой должна равняться единице, то необходимо выбрать К = 1/6,18. Так как в городе К. 30000 жителей (имеются в виду
жители в возрасте от 5 до 80 лет), а каждый житель ежедневно платит за свой проезд 4*17 рублей, то за месяц он заплатит 30*4*17 рублей, то есть месяч
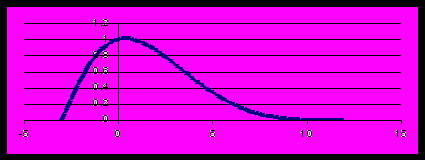
Рис. 3. К методике нахождения параметра K.
ный доход транспортной компании равен 30000*30*4*17 = 61,2 млн. руб.
Теперь необходимо рассчитать, сколько процентов площади под кривой распределения лежит правее икса, соответствующего возрасту 60 лет. Это и будет процент дохода, потерянный компанией из-за распоряжения мэра Стручкова. Так как отрезок [-3,016; 12,042] является просто как бы уменьшенной копией отрезка от 5 до 80 лет, то для расчета значения «х», соответствующего возрасту 60 лет, составляем пропорцию:
(х + 3,016)/15,058 = (60 – 5)/75. Отсюда х = 8,027. Вычислим площадь на отрезке [8,027 ; 12,042] тем же методом, что и выше. Получим число 0,0062 (то есть 0,62% всей площади). Это число получилось малым из-за того, что делалось неочевидное предположение: чем человек старше, тем он реже пользуется транспортом. Так как для другой (более реалистичной) кривой распределения пользователей транспорта по возрасту вычисления делаются по той же схеме, то доведём их до конца. А именно, компания потерпит убыток в 0,0062*61,2 млн. руб. = 337216 рублей.
Задание 13.
Расчет кривой спроса построением параболической и синусоидальной регрессии
Пояснения для преподавателей. Кривая спроса для неограниченно делимого товара может считаться непрерывной (и даже гладкой) функцией. Она должна быть убывающей и выпуклой вниз. Подобного рода кривых имеется много в арсенале математики. Расчет кривой спроса обычно делается построением регрессии на основе нескольких эмпирических точек (p, q), где p - цена товара, постоянная в течение рассматриваемого периода времени, q – суммарное количество, купленное потребителями в течение данного периода. В объясняемых координатах этих точек «спрятаны» случайные погрешности. Мы будем считать, что объясняемой переменной является q. Случайные погрешности (отвечающие условию гомоскедастичности) добавлены к базовой зависимости q = f(p) методом генерации случайных чисел на компьютере. Затем производится подгонка параболической кривой и синусоидальной кривой (на участке, кде она убывает и выпукла вниз). Качество подгонки и для той, и для другой регрессионной кривой проверяется путем расчета минимальной суммы квадратов регрессионных остатков и сравнения этих двух сумм. В качестве товара взят картофель. Чтобы не возникало лишних вопросов о поведении кривой спроса при стремлении p к нулю и к бесконечности, эта кривая рассматривается в диапазоне от 5 до 50 рублей (ориентировка на стоимость килограмма картофеля).
Постановка задачи
Задано пятнадцать точек на кривой спроса: (данные о месячной продаже картофеля в пятнадцати однотипных посёлках)
Руб. 9 11 11 13 15 19 20 20
Кг 4800 3900 3800 3500 3200 2900 2800 2800
Руб. 21 23 27 27 28 30 37
Кг 2800 2700 2600 2600 2500 2500 2400
Сделать расчет, при какой цене будет раскуплено за месяц ровно 3000 кг картофеля. Для этого рассчитать регрессию в двух вариантах:
а) вида y = a x2 + b x + c (13.1)
б) вида y = A sin(π x /30) + B cos(π x /30) + C (13.2)
Оценить, какая регрессия лучше.
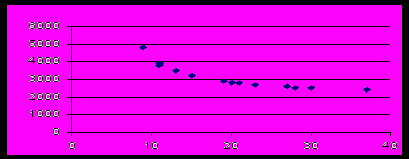
Ход решения
Сначала студент представляет исходные данные графически (следует обратить внимание на то, что кривизна в начале линии спроса больше, чем в конце).
Затем вычисляются коэффициенты параболической регрессии по формуле вида ЛИНЕЙН(E1:E15;F1:G15;1;1) , где в столбце E расположены значения объясняемой переменной, в столбце F – квадраты значений объясняющей переменной, в столбце G – просто значения объясняющей переменной. Первая единица означает, что нужно учесть постоянное слагаемое, а вторая единица – что надо вывести на экран статистические показатели регрессии. Нажав на Enter, можно увидеть один из коэффициентов рассчитанной компьютером регрессиии (какой именно – будет указано ниже).
Чтобы увидеть все данные по регрессии, следует выделить вправо и вниз область, достаточную для размещения всей информации (если будет выделена ячейка, в которой нет данных, то она будет помечена как Н/Д). Затем надо щелкнуть мышью на строке с формулой (формула от этого изменит свой цвет), и нажать комбинацию клавишей Ctrl+Shift+Enter. Ниже показано, что в этом случае получилось на экране:
-251,8 4,1205 6251,759 #Н/Д
33,199 0,7487 338,9115 #Н/Д
0,9303 191,9 #Н/Д #Н/Д
80,042 12 #Н/Д #Н/Д
6E+06 441924 #Н/Д #Н/Д
В первой строке представлены искомые коэффициенты регрессии. На последнем месте располагается постоянное слагаемое (если оно предусмотрено формулой регрессии). На втором месте представлен коэффициент при квадрате объясняющей переменной (обратите внимание: в исходных данных квадраты были записаны раньше, чем первые степени, а коэффициент при квадрате выдается на экран позже (так устроен пакет Excel)). Наконец, на первом месте представлен коэффициент при первой степени. Итак, первый вариант формулы для регрессии имеет вид:
y = 4,12 x2 – 252 x + 6252.
Во второй строке представлены средние квадратичные отклонения, даваемые формулами для вычисления коэффициентов регрессии (в курсовой не используются). Из оставшихся чисел обратим внимание только на три:
0,9303 (коэффициент детерминации),
12 (число степеней свободы в исходных данных); оно равно 15 – 3 (всего данных 15, но три из них как бы «потрачены» для оценки a, b, c),
441924 – остаточная сумма квадратов.
Графически исходные и регрессионные точки изображаются так (см. рис. 4). Рассмотрим теперь расчет синусоидальной кривой регрессии по тем же 15-и точкам. Хотя в формуле (13.2) имеется и синус, и косинус, итоговая кривая все же будет синусоидой, но растянутой и смещенной вдоль осей OX и OY. В описании регрессии участвует только небольшой кусок этой синусоиды. Как и раньше, заносим столбец значений игреков, а за ним – столбцы со значениями синуса и косинуса в соответствии с формулой (13.2) (столбец иксов в данной модели не нужен). Получаем результаты:
1163 -74,964 3543,759
156,4 185,49 168,2931
0,8768 255,07 #Н/Д
42,702 12 #Н/Д
6E+06 780747 #Н/Д
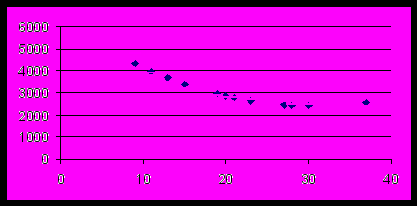
Рис.4. Параболическая модель регрессии (квадратики).
Черточки – исходные данные.
Теперь уравнение регрессии имеет вид
y = -75,0 sin(π x /30) + 1163 cos(π x /30) + 3544
На рис. 5 эта кривая сравнивается с исходными точками.
Заменяя «у» на 3000 и решая полученное уравнение (квадратное или тригонометрическое), мы и получаем искомую цену «х» в каждом из двух случаев
Осталось ответить на ворос, какая из регрессий лучше. Если судить по математическим показателям, то первая лучше: у нее больше коэффициент детерминации (0,9303 > 0,8768), и у нее меньше сумма квадратов (441924 < 780747). Причиной последнего обстоятельства является то, что синусоида слева искривлена меньше, чем справа. А у исходной кривой --– наоборот, слева кривизна больше. С точки же зрения экономики они «обе хуже», так нарушают основное свойство кривой спроса: она должна монотонно убывать, а на обоих кривых регрессии просматривается точка минимума. Как же быть? Искать другие кривые регрессии! (Такой поиск вполне можно доверить студенту-отличнику. Подскажем, что исходная кривая является дробно-линейной функцией, «запылённой» случайными ошибками. Так было задумано автором задания. Значит, и регрессию разумно искать в таком виде).
Если же всё же доводить до конца решение именно с этими регрессиями, то надо из двух корней квадратного уравнения (или из многих корней тригонометрического уравнения) надо отобрать только один, лежащий в экономически допустимых пределах
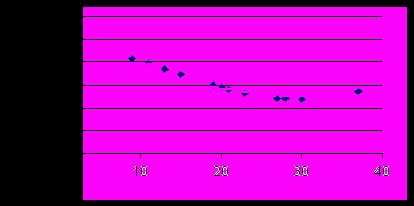
Рис. 5. Синусоидальная регрессия.
Задание 14.
Рекламная акция по продаже «Сникерсов». Расчет прибыли методами ЛИФО и ФИФО
Пояснения для преподавателей. В начале перестройки (в 1991 году) в конце улицы Арбат продавали «Сникерсы», чтобы приучить российских потребителей к новому виду продукции. «Сникерсы» продавались по смехотворно низкой цене (примерно по два рубля за штуку, в переводе на нынешние деньги). Естественно, в очереди наблюдалось несколько старушек с кошёлками, которые закупали продукцию по несколько десятков штук, быстро смекнув, что в Подмосковье её можно будет перепродать намного дороже. В связи с этим возникает вопрос: не сорвут ли такие старушки, заполонив всю очередь, рекламную акцию производителей «Сникерсов» ? По-видимому, разумно постепенно повышать розничную цену. От этого дальнейший рост перекупщиков в очереди сильно сократится, а оставшиеся старушки будут закупать всё меньше и меньше «Сникерсов», опасаясь, что не все их удастся распродать. Но тогда мы попадаем в классическую ситуацию, когда меняется со временем закупочная цена «сырья», то есть при исчислении прибыли необходимо использовать один из разрешенных в России методов расчета стоимости запасов. В данной курсовой выбраны методы ЛИФО и ФИФО. Кроме того, считается, что «рыночные» (не рекламные) цены реализации «Сникерсов» изменяются случайным образом (но всё же постепенно нарастают). После формализации описанных общих соображений мы и получаем формулировку задания для курсовой.
Постановка задачи
Фирма, проводящая рекламную акцию в России по продаже «Сникерсов» по постепенно нарастающей цене (от «рекламного» до «рыночного» уровня), заключила договор с российской фирмой-посредником «Не тормози, сникерсни!» о том, что посредник будет каждые две недели закупать у производителя товар по следующей схеме: 16 единиц по 1 руб. за «Сникерс» (единицей считается упаковка, содержащая 1000 шт. товара); затем 15 единиц по по 2 рубля, затем 14 единиц по 3 руб., 13 единиц по 4 руб., и так далее до 1 единицы по 16 руб. за штуку товара. Исходная рыночная цена «Сникерса» равна 5 руб/шт., но прогнозируется, что она будет нарастать (так как россиянам понравится этот товар) примерно до 12 руб. за штуку. Таким образом, посредник, исходя из этого прогноза, сначала будет иметь крупную прибыль, а конце будет терпеть убыток. В целом, конечно, посредник надеется, что прибыль в начале с лихвой компенсирует убыток. Поставщик же заранее идет на убыток, так как акция носит рекламный характер. Тем не менее, в договоре предусмотрена уплата крупной неустойки как посредником, так и поставщиком, если они нарушат этот договор. (Студент должен сам сформулировать, почему в этой ситуации возможно нечестное поведение как одной, так и другой договаривающейся сторны).
Посредник принял решение в конце каждого месяца распродавать все закупленные в этом месяце упаковки, кроме одной. Тем самым на складе у посредника постепенно нарастает то, что в логистике называется «страховым запасом товара». Благодаря наличию такого запаса, состоящего из упаковок, закупленных в разное время и по разной цене, подсчет прибыли посредника в конце каждого месяца должен призводиться тем или иным методом списания запасов на себестоимость. В данной курсовой предлагается использовать методы ЛИФО и ФИФО и сравнить их между собой.
Вместо подсчета стоимости упаковок, ушедших со склада, достаточно рассчитать стоимость запаса, оставшегося на складе (это будет проще и позволит глубже понять суть методов ЛИФО и ФИФО).
Чтобы смоделировать случайные значения рыночной цены «Сникерса», нарастающие в среднем от 5 (в конце первого месяца) до 12 (в конце 8-го месяца) рублей, студент должен написать уравнение прямой, проходящей через точки (1, 5) и (8, 12), и в конце каждого месяца прибавить к ней случайное число, равномерно распределенное от (-2) до 6 рублей.
Для выполнения этой курсовой необходимо рассчитать прибыль посредника в конце каждого из восьми месяцев методами ЛИФО и ФИФО и представить результаты графически на одной и той же гистограмме.
Ход решения
Напомним суть методов ЛИФО и ФИФО (подробнее о них можно прочитать в любом серъёзном учебнике по бухучёту, например в учебнике Кондракова). Обозначим через q1, q2, q3, … количества товара, поступающие на склад в моменты времени 1, 2, 3, … . Через p1, p2, p3, … обозначим закупочные цены товара, которые имели место на рынке в моменты 1, 2, 3, … Наконец, через Q1, Q2, Q3, … обозначим количества, уходящие со склада в призводство или на продажу в моменты 1, 2, 3, … Чтобы не возникало недоразумений, будем считать, что в один и тот же момент времени не может происходить и приход, и уход товара.
На печати будем изображать значения q, p, Q обычным, курсивным и жирным шрифтом соответственно. Например:
17(4), 15, 10 (6), 7, 10 (9), 8, …
Выше рассмотрены шесть разных моментов времени (неважно, какие именно эти моменты; но важно знать, какой из них раньше, а какой позже). На обычном языке эта строка расшифровывается так: «Сначала склад был пуст. В 1-й момент на него поступило 17 шт. товара по цене 4 руб/шт. Во второй – со склада ушло 15 штук. В 3-й момент поступило еще 10 штук такого же товара, но по цене 6 руб/шт. Затем ушло 7 штук, потом пришло 10 (по 9 рублей), в 6-й момент ушло 8, и так далее.».
Таким образом, физический поток товара описан полностью. Но его сопровождает и финансовый поток (бухгалтерские проводки по оприходованию товара и по его списанию со склада). Если с приходом товара всё ясно (если пришло 17 физических единиц по цене 4 руб/шт, то оприходовано 68 финансовых единиц <рублей>), то с уходом товара иногда возникает недоумение: по какой цене списать ушедший товар? Так, когда ушло 15 единиц товара, было ясно, что каждая из них «унесла» с собой 4 рубля (так как все единицы на складе стоили 4 рубля). На складе остались две единицы по 4 рубля. Затем поступили ещё 10 единиц по 6 рублей. А после этого со склада надо отгрузить 7 единиц, но по какой цене? Две единицы по 4 рубля, прочие по 6? Или все по 6 рублей? Или ещё как-нибудь?
Вот тут-то нам и приходят на помощь методы ЛИФО и ФИФО. Каждый из них позволяет внести ясность в поставленный выше вопрос. Метод ФИФО (FIFO; first input – first output) приказывает раньше списывать со склада тот товар, который поступил раньше. В противоположность ему, метод ЛИФО (LIFO; last input – first output) предписывает отгрузку товара «с конца» - сначала списывают со склада единицы товара, поступившие последними (пока все они не будут выбраны), затем – предпоследними, и так далее.
При поверхностном взгляде на этот вопрос в голову сразу приходит мысль, что метод ФИФО «справедливый», а ЛИФО – «несправедливый» (так как приспособлен для обслуживания нахалов, рвущихся без очереди). На самом деле это, конечно, не так. Имеются ситуации, когда нужно применять метод ЛИФО и вообще невозможно применить метод ФИФО. Например, при программировании надо возвращаться сначала в ту подпрограмму, из которой вышел позже всего, потом – в предыдущую, и так далее. Что же касается бухгалтерии (и логистики), то между учёными долго тянулся спор о законности и преимуществах этих методов, но в итоге было осознано, что оба метода логиески равноправны и вполне могут использоваться для целей учёта. Тем не менее, финансовые результаты за данный период времени, рассчитанные этими методами, могут сильно различаться. Это вовсе не значит, что таким образом «из воздуха» непонятным образом возникают лишние деньги. Просто сумма, не добранная в этом периоде, будет дополучена в каком-то другом периоде времени.
Сначала рассмотрим метод ЛИФО. Согласно ему, надо все семь единиц товара списать по цене последнего прихода товара, то есть по 6 рублей. На складе останется 5 единиц, из них две по цене 4 руб/шт, прочие три – по 6 рублей. (Конечно, на складе все 5 штук лежат в одной куче, так как физически они ничем не отличаются. А различие в цене отразилось лишь в документах склада и бухгалтерии). На складе остались «лежать» 2*4 руб. + 3*6 руб., воплощенные в стоимости пяти единиц товара.
Теперь применим метод ФИФО. Сначала спишем самые ранние единицы товара, то есть две шт. по 4 рубля. Затем спишем ещё пять шт. по 6 руб. На складе остались, в виде стоимости товара, 5*6 руб.
Рекомендуется довести до конца эти рассуждения: как следует производить списание следующих 8 единиц товара?
Опыт преподавания методов ЛИФО и ФИФО привёл автора в убеждению, что даже способные студенты, вроде бы схватившие на лету алгоритмы ЛИФО и ФИФО (тем более, что звучат они обманчиво просто), не понимают, какие крупные подводные камни могут им встретиться на этом пути. Поэтому в качестве первой (и главной) части курсовой работы предлагается заполнить следующую таблицу из восьми групп операций; в каждой группе имеется две операции прихода товара и одна операция ухода. Эти операции описаны выше, в постановке задачи. После каждого ухода товара надо подсчитать, сколько рублей осталось на складе согласно бухгалтерским документам (один раз – методом ЛИФО, другой – методом ФИФО). Первые две из восьми групп уже заполнены (надо только понять, почему они именно так заполнены). Остальные надо заполнить самостоятельно и обсудить результаты с преподавателем.
Рублевые остатки на складе (двумя методами) Остат.на складе
(тысяч рублей)
тыс.шт. руб/шт тыс.шт. руб/шт ФИФО ЛИФО
нач.янв. 16 1 серед.янв. 15 2
отгрузка 30 2 1
нач.фев. 14 3 серед.фев. 13 4
отгрузка 26 8 4
нач.мар. 12 5 серед.мар. 11 6
отгрузка 22 18 9
нач.апр. 10 7 серед.апр. 9 8
отгрузка 18 32 16
нач.мая 8 9 серед.мая 7 10
отгрузка 14 50 25
нач.июн. 6 11 серед.июн. 5 12
отгрузка 10 72 36
нач.июл. 4 13 серед.июл. 3 14
отгрузка 6 98 49
нач.авг. 2 15 серед.авг. 1 16
отгрузка 2 128 64
Подчёркнутые данные в группах 3-8 – это попытка некоторого студента решить данную задачу. Данные подчёркнуты потому, что это решение неверное, и это легко доказать. В самом деле, после каждой отгрузки на складе оставалась одна не распроданная упаковка «Сникерсов». После 8-й отгрузки их осталось восемь, а общая их стоимость (посчитанная методом ФИФО) равна 128 тыс. рублей, то есть 8 раз по 16 тысяч. Но по цене 16 тысяч на склад поступила только одна упаковка. Значит, это число явно завышено, то есть хотя бы одно неверное число среди подчеркнутых есть. А вот с какого места начинаются ошибки, сколько их, и как их исправить – это задача для студента, выполняющего данную курсовую. Пока в этом вопросе не появится ясности, нельзя считать, что методы ЛИФО и ФИФО поняты до конца!
Во второй части курсовой работы следует 10 раз смоделировать случайное нарастание рыночной цены на «Сникерсы» и каждый раз вычислить суммарную прибыль посредника (один раз - по методу ЛИФО, другой раз – по методу ФИФО). Найдя среднее арифметическое прибылей для каждого из этих методов, сделайте вывод о том, какой из методов выгоднее для посредника. Прибыль от перепродажи вычислять как разность между стоимостью приобретения товара и ценой его реализации в конце месяца. Для примера ниже приведены 8 цен на «Сникерсы» для одного из десяти планируемых случайных испытаний (цены даны в рублях, на конец месяца):
3,37
4,94
5,98
8,03
11,68
13,16
16,45
16,06
На методы ЛИФО, ФИФО и средней себестоимости можно подготовить целую серию разных курсовых изложенного выше типа.
Кроме этих трех методов, в практике работы предприятия используются и другие подобные методы. Например, LOFO, HIFO, KIFO (первый из них требует списания запасов, в первую очередь, по более низкой цене покупки; второй – по более высокой, а третий, расшифровывающийся как «Konzern input – first output», в первую очередь списывает запасы, произведенные на этом концерне (предприятии)). Как говорится, «не буди LIFO, пока спит тихо…».
Задание 15.
Прогноз дохода от земельного участка за пять лет (множественная регрессия с двумя объясняющими переменными)
Замечания для преподавателей. Давно уже стали притчей во языцех неграмотные модели множественных регрессий для расчета ориентировочной стоимости квартиры в Москве, в которых учитываются до шести объясняющих переменных, каждая из которых может меняться непрерывно или является дискретной и имеет 9-22 значений (например, номер этажа, на котором находится квартира). При этом для расчета используется только 70-80 данных о последних проданных квартирах такого типа, «потому что надо отбирать данные при прочих равных условиях, а этих условий (то есть параметров квартир) можно насчитать до 25-и и более – как их все сделать равными?». В такой ситуации лучше вообще отказаться от составления регрессии, чем вводить в заблуждение широкие массы покупателей квартир. В то же время имеются экономические ситуации, где и данных много (100-120 точек), и картина ясна с геометрической точки зрения (например, нахождение плоскости регрессии с учётом двух объясняющих переменных и постоянного слагаемого), поэтому построение множественной регрессии вполне уместно и приносит практическую пользу. На занятиях по эконометрике ввиду малого количества часов множественные регрессии подробно рассмотреть не удаётся, так что предлагаемая ниже курсовая послужит хорошим практическим закреплением изученных в теории понятий.
Постановка задачи
Имеется квадратное поле размерами 1000 м на 1000 м, на котором урожайность картофеля зависит от двух факторов: степени увлажнения почвы и количества в ней перегноя. Вследствие особенностей расположения поля и состава его почвы фактор увлажнённости линейно нарастает при движении по одной стороне поля (ось ОХ) независимо от степени смещения по другой стороне (ось OY). Фактор количества перегноя аналогичным образом нарастает линейно вдоль оси OY. Поле разбито на 400 квадратных делянок со сторонами 50 м на 50 м, и в течение десяти предыдущих лет на каждой делянке фиксировался собранный урожай, а в центральной части делянки брались пробы почвы на влажность и на содержание перегноя. Пробы на влажность делались через месяц после посадки картофеля, а на перегной – после уборки урожая. Пробы на влажность необходимо усреднить по 10-и годам, чтобы сделать их более независимыми от погодных условий в конкретном году, а по пробам перегноя сделать вывод о скорости истощения почвы с течением времени. Данные об урожайностях на конкретной делянке также надо усреднить по 10-и годам.
Конкретные исходные данные будут даны преподавателем после беседы со студентом. Требуется рассчитать пять множественных регрессий (с учетом постоянного слагаемого) для прогноза урожайности поля на следующие пять лет (с учетом постепенного истощения перегноя в почве). Использовать их для суммарного прогноза выручки от продажи картофеля в ближайшие пять лет.
