Пошаговое приближение распределения стоимости покупки к нормальному закону распределения
| Вид материала | Закон |
| Себест. Курс долл. Курс евро Ход решения Пояснения для преподавателей. Имя заемщика Ход решения Постановка задачи (напоминание) Ход решения Треугольники на диаграмме – исходные данные |
- Лабораторная работа 1-08 экспериментальное изучение гауссовского закона распределения, 108.63kb.
- Дискретные случайные величины Ряд распределения, 29.73kb.
- Природа каналов распределения товаров. Их структура и управление, 20.88kb.
- Лабораторная работа №2 Тема: Формирование выборки случайных чисел, распределенных, 151.75kb.
- Функция распределения. Плотность распределения. Основные параметры непрерывных случайных, 7.05kb.
- Законом распределения, 13.27kb.
- Методы и каналы распределения товаров, 82.28kb.
- Лекция 10. Управление системой распределения >10. Управление системой распределения, 258.27kb.
- Задача оптимизации расположения распределительного центра на обслуживаемой территории, 872.4kb.
- Секция №1 Модераторы: В. Стрельченок, Е. Толстая, И. Ратанова, 183.54kb.
Себест. Курс долл. Курс евро
4111 33 27
4041 32 28
3699 28 30
4028 31 31
4089 31 33
3869 30 29
4000 31 30
3800 29 30
3742 29 28
Требуется найти оценочные значения коэффициентов линейной регрессии, выражающей себестоимость сапог P через курс доллара D и курс евро E (представить промежуточные расчеты с пояснениями, а также оценку ошибки, даваемой формулой регрессии для девяти приведенных выше наблюдений). Регрессию взять без постоянного слагаемого (возможное экономическое объяснение этого: в себестоимость не входит оплата труда рабочих, так как они выполняют её в порядке благотворительности). Работа ориентирована на решение методом проекции вектора на подпространство. Варианты ответов (один из них – почти правильный):
1) P = 100,27 D + 29,71 E
2) P = 40 D + 25 E
3) P = 20,2 D + 28,7 E
4) P = 90,11 D + 29,71 E
5) P = 10,75 D + 29,01 E
Указать, к какому из вариантов ближе всего правильный ответ
Ход решения
Будет рассмотрен только случай, когда изменяются только значения объясняемой переменной, лежащие в середине списка. При этом верный ответ, который раньше почти совпадал с первым, перейдёт в верный ответ, практически равный ответу номер четыре (P = 90,11 D + 29,71 E ). Студенту даётся для самостоятельной рахзработки один-два подобных же случая.
Первый вариант «Задачи о женских сапогах» может быть решён в пакете Excel по команде ЛИНЕЙН(A1:A9;B1:C9;0;1). Результаты решения приведены ниже:
| 29,71271 | 100,2747 | 0 |
| 0,146703 | 0,142484 | #Н/Д |
| 0,999957 | 1,091398 | #Н/Д |
| 81507,71 | 7 | #Н/Д |
| 194175,7 | 8,338044 | #Н/Д |
| #Н/Д | #Н/Д | #Н/Д |
| #Н/Д | #Н/Д | #Н/Д |
Получена плоскость регрессии z = 100,27 x + 29,71 y. Отсюда видно, что правильным является первый вариант ответа. Теперь используем пункт меню Сервис, Поиск решения для подгонки значений себестоимости (располагающихся со второго по пятое место) таким образом, чтобы правильным ответом стал четвёртый. Чтобы добиться этого, рассмотрим следующую целевую функцию
f = (F1–90,11)2 + (E1–29,71)2 , где
F1 – та ячейка, в которой размещается коэффициент 100,2747 ;
E1 – та ячейка, в которой размещается коэффициент 29,71271 .
Теперь найдём минимум указанной целевой функции, разрешая компьютеру изменять ячейки, в которых хранятся значения себестоимостей
4041
3699
4028
4089
3869
При этом наложим ограничения, что каждая из этих ячеек не может быть меньше 3000. После выполнения оптимизации получаем новые значения себестоимостей:
3151
3367
3481
3704
3258
Значение целевой функции после оптимизации равно 0,0048.
Теперь с новым столбцом себестоимостей из девяти чисел (пять из которых – только что подобранные) по той же формуле делаем расчёт регрессии. Ответ
:
29,76096 90,06321 0
47,15829 45,80221 #Н/Д
0,014223 350,835 #Н/Д
0,050498 7 #Н/Д
12431,13 861596,4 #Н/Д
Получена регрессия z = 90,06 x + 29,76 y , которая весьма близко совпадает с четвёртым ответом.
Задание 19.
Определение степени оправданного риска при выдаче банком потребительских ссуд
Пояснения для преподавателей. Постановку этой задачи и некоторые исходные данные автор позаимствовал из монографии D. N. Chorafas “Systems and Simulation” (New York, 1965).
Руководство коммерческого банка, желая поставить на научную основу работу своего кредитного отдела в части обслуживания физических лиц, предложило специалистам по исследованию операций разработать «форму для оценки клиента, пришедшего за ссудой». Главная цель руководства банка – установить и формализовать для неспециалистов некоторые правила для определения степени «оправданного риска», на который банк должен идти, чтобы повысить матожидание своей прибыли.
Постановка задачи
Прибыль банка зависит от ссудного процента, числа выдаваемых ссуд и доли невозвращаемых ссуд. Ниже приведены сведения о количестве заёмщиков (в общем числе 4100), попадающих в интервалы величины займа (0,100), (100,200), … , (1400,1500):
300 700 1000 575 400 250 185 155
130 105 70 85 65 55 25
В отделе потребительского кредита банка удалось получить следующие усреднённые сведения: ежегодно выдаётся 2000 ссуд размером от 0 до 300 долларов, а также 20000 ссуд размером от 300 до 1500 долларов. По ссудам первого типа банк взимает 10%, а второго – 6%.
90% пользователей погашают ссуду в срок, 5% - после нескольких напоминаний, 3% - только при реальной угрозе судебного преследования, 1% - погашают тогда, когда банк уже списал её в убыток, и 1% - не погашают вообще.
Для оценки качества заёмщиков клерками банка разработана следующая форма:
Имя заемщика
Номер заявления
Служеб. положение
Место работы
Дата подачи заяв.
Размер запрашив. суммы
Оценка факторов, влияющих на риск:
Стабильность пребывания на одной работе J___
Доход N___
Дробь доход/сумма K___
Отсутствие задолженности L___
Способность погасить ссуду B___
Отношение к погашению задолженности P___
Стабильность проживания на одном месте E___
Личные склонности/привычки S___
Занятие Q (по списку риска этих занятий) ___
Текущая предельно допустимая константа риска __
Расчетная константа риска R__
Рекомендация рассмотрителя заявки _____________
Пояснения. Факторы J, N, K, L, B, P, E, S, Q оцениваются рассмотрителем (клерком банка) количеством баллов от 4 (превосходно) до 1 (плохо). Константа риска R является взвешенной средней этих девяти факторов, причем фактор B берется с весом вдвое больше остальных факторов, фактор же P – с весом втрое больше. В итоге применяется формула
R = (J + N + K + L + 2B +3 P + E + S + Q) / 12
По этой формуле константа R всегда будет лежать в пределах от 1 до 4 (чем меньше R, тем хуже заемщик).
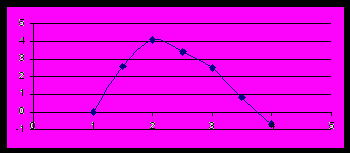
Фактически эта формула является эмпирически подобранной упрощенной множественной регрессией. Изучение зависимости процента потерянных ссуд (по приведенным выше данным) и числа выданных ссуд (с учетом их распределения по интервалам) от константы риска R позволило построить график ожидаемого процента прибыли от выдачи ссуды данному заемщику от той же константы R (см. рис. ниже).
В связи с этим исследованием клеркам банка была дана рекомендация выдавать ссуду только тем просителям, у которых (при прочих равных условиях) константа R лежит в оинтервале от 1,5 до 3.
Сгенерировать поток заявок объёмом 1000 реализаций, где случайным образом будут заданы упомянутые выше показатели J, N, K, L, B, P, E, S, Q (с равной вероятностью принимающие значения 1, 2, 3, 4) для каждого из 1000 заёмщиков данного года, а также просимые величины ссуд (от 0 до 1500 долларов), соответствующие приведенной выше частоте выдачи ссуд. Среди этих 1000 реализаций должно быть 10% заемщиков, которые не вернут вклад (но этот факт клерку банка останется неизвестным), причем не возвращать вклады могут и заемщики группы ссуд до 300 долларов, и прочие заёмщики. После расчета показателя R для каждого заемщика сделать отсечку просителей согласно неравенству 1,5 < R < 3 и затем для каждого из оставшихся рассчитать прибыль банка (учесть, что процент прибыли иногда равен 10%, а иногда 6%). Подтверждается ли в этом случае приведенная выше кривая прибыли?
Ход решения
Порядок генерации значений дискретной случайной величины с заданными вероятностями этих значений описан в методическом пособии:
Савватеев В. В. Профессиональные навыки работы бухгалтера на персональном компьютере. – М.:Изд-во Рос. экон. акад., 2002.– 24 с.
Гистограмму распределения количеств заемщиков по интервалам величин вкладов удобно заменить аналитической формулой y = Ax exp(-Bx). Параметры A, B подбираются с помощью процедуры Поиск решения в пакете Excel. Подробности изложены в задании 20. Поэтому задания 19, 20 удобно делать паре студентов (один рассчитывает кривую y = Ax exp(-Bx), а другой проверяет обоснованность правила отбора заемщиков).
Задание 20.
Подбор параметров нелинейной регрессии
Постановка задачи (напоминание)
Прибыль банка зависит от ссудного процента, числа выдаваемых ссуд и доли невозвращаемых ссуд. Ниже приведены сведения о количестве заёмщиков (в общем числе 4100), попадающих в интервалы величины займа (0,100), (100,200), … , (1400,1500):
300 700 1000 575 400 250 185 155
130 105 70 85 65 55 25
Гистограмма по этим данным имеет вид (интервалы по 100 долл.):
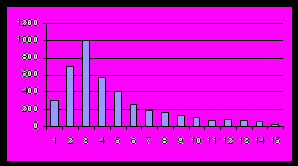
Требуется рассчитать коэффициенты нелинейной регрессии вида y = Ax exp(-Bx). (Этот вид соответствует ходу изменения значений гистограммы).
Ход решения
Так как сумма всех частот равна 4100, а основание каждого прямоугольника равно 100 долл., то общая сумма вкладов равна 410000 долл. Каждый прямоугольник привяжем к середине интервала. Получаются точки (50, 300), (150, 700), … , (1450, 25).
Возьмем логарифмы от обеих частей уравнения:
ln y = ln A + ln x – B x
Обозначая ln y = z, ln A = a, ln x = w, будем искать регрессию
z = k1*x + k2*w + k3.
Для этого у нас имеются 15 значений величины z (логарифм от частоты), играющей здесь роль объясняющей переменной, 15 значений середин интервалов x = 50, 150, 250, … , 1450, и логарифмы от них ( = w).
Результат обращения к функции ЛИНЕЙН:

Итак, k3 = 3,835; k2 = – 0,00333; k1 = 0,5983.
Поэтому линеаризованное уравнение имеет вид:
ln y = 3,835 + 0,5983 w – 0,00333 x ( где 3,835 удобно записать как ln 46,29). Отсюда y = 46,29* x0,5983 * exp(–0,00333 x)
По поводу этой формулы надо сделать три замечания:
1. Найдена формула не того вида, который мы хотели найти (в ней «х» содержится в степени 0,5983, а не в первой степени). Она, тем не менее, выражает особенности поведения гистограммы (см. рис. ниже), и студент, выполняющий эту курсовую, должен сам изменить постановку задачи, чтобы в решении не возникал «порочный круг».
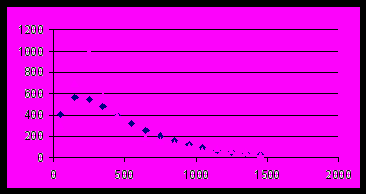
Треугольники на диаграмме – исходные данные
2. Процедура предварительного взятия логарифма исказила поведение кривой в окрестности точки максимума, так сумма квадратов отклонений, наименьшая для логарифмов, может не быть наименьшей для исходных значений. Поэтому рассчитанную кривую следует подогнать с помощью процедуры пакета Excel Поиск решения.
3. Видимо, надо подгонять кривую отдельно на участке (0, 300) и на участке (300, 1500). (См. задание 19). Так как это усложняет формулировку курсовой, такую подгонку можно предложить сделать только студенту, претендующему на отличную оценку.
В заключение приведем типовой список тем с маркетинговым содержанием, к которым и будут подбираться задания по статистике и эконометрике, изложенные выше. Темы подготовлены преподавателями кафедры Маркетинга РЭА им. Г.В. Плеханова.
Тематика
междисциплинарных курсовых работ по комплексу
«Маркетинг, поведение потребителей и эконометрика»
1. Современный потребительский рынок России и портрет российского потребителя (на примере товара, региона, социальной группы и т.д.)
2. Маркетинговые исследования как основа знаний компании о поведении её потребителей.
3. Использование результатов исследования потребителей для построения комплекса маркетинга компании.
4. Применение возможностей Интернета в маркетинговой деятельности компании для воздействия на поведение потребителей.
5. Сегментирование рынка и его значение для изучения поведения потребителей (на примере отдельных сегментов).
6. Влияние особенностей маркетинговой информации в России на проведение исследований потребителей.
7. Измерения и разработка форм для сбора данных для выявления мнения потребителей о товаре.
8. Разработка оценочных критериев при определении отношения потребителей к компании и её товару (услуге).
9. Применение мультиатрибутивной модели отношений М. Фишбайна в изучении поведения потребителей.
10. Промышленный маркетинг и процесс принятия решения о закупке товаров и услуг компаниями и организациями.
11. Глобальные потребительские рынки: кросс-культурные различия в поведении потребителей.
12. Маркетинговая направленность международной системы управления качества товаров и услуг, предлагаемых потребителям.
13. Факторы макросреды компании и получение социально-экономической информации о потребителях с помощью данных государственной статистики.
14. Национальные субкультуры: характеристика, особенности, значение для маркетинга.
15.Знание процессов потребления товаров (услуг) и освобождения от использованных товаров как один из факторов удержания потребителей компании.
16. Экономические, временные и познавательные ресурсы потребителей и их связь с маркетинговой стратегией компании.
17. Личность, ценности и стиль жизни – детерминанты построения программ коммуникации компании с потребителями.
18. Реакция потребителей на рекламную деятельность компании и процесс восприятия.
19. Использование когнитивного и бихевиористского подхода обучения в маркетинговых коммуникациях.
20. Взаимосвязь между жизненным циклом семьи, поведением потребителей и комплексом маркетинга компании.
21. Российское законодательство о защите прав потребителя и реалии и этика маркетинга.
22. Типы инноваций товаров и услуг и их воздействие на поведение потребителей.
23. Основные подходы к теории личности и их использование в маркетинговой деятельности компании.
24. Влияние ситуации на поведение потребителей и маркетинговую деятельность компании.
25. Семья, её основные функции и роль в формировании будущих потребителей товаров и услуг.
26. Влияние персональных продаж на процесс принятия решений о закупках в сфере B2B.
27. Изменение роли женщины как потребителя и ее воздействие на маркетинг товаров и услуг.
28. Референтные группы и их воздействие на поведение потребителей и маркетинговую стратегию компаний.
29. Социальный статус людей и использование его концепции в маркетинге.
30. Культурные аспекты маркетинга и социализация потребителей.
Замечание. Многие из заданий, изложенных выше, носят логистическую направленность. Поэтому в перспективе этот список тем будет пополнен типовыми темами КМКР по логистике.
Рисунок, приведенный ниже. иллюстрирует процесс обсуждения статистической части одной из курсовых работ.


