Пошаговое приближение распределения стоимости покупки к нормальному закону распределения

Вид материала

Подобный материал:

1 2 3 4 5 6 7 8 9 10 11

Постановка задачи

Торговое предприятие завозит арбузы из Астрахани в Москву, пользуясь открытым сверху контейнером размеров 6 м х 3 м х 1,5 м. 50% (по количеству штук) арбузов – крупные (средний вес 10 кг). Остальные 50% - средние (средний вес – 7 кг). Удельный вес арбуза примерно равен единице. В первом приближении форма арбуза шаровая, в более точном приближении – это сплющенный эллипсоид вращения. Рассчитать количество арбузов, помещающееся в контейнере при укладке слоями, где слой крупных арбузов чередуется со слоем средних, а в каждом слое (крупных арбузов) у арбуза, не лежащего на границе, имеется ровно 6 примыкающих к нему соседей («шестиугольная укладка»). Имеются данные о реально проданном количестве арбузов за предыдущие 66 привозов товара. Проверить гипотезу о том, что часть арбузов из заполненного контейнера сначала продавалась «налево», а остальные уже попадали в официальную отчетность. Уровень достоверности проверки гипотезы взять равным 95%.

Пояснения для преподавателей. Предложена стандартная статистическая задача на проверку гипотезы методом использования распределения Стьюдента. Такого рода проверки гипотез часто осуществляются в ходе проведения инспекций и аудиторских проверок. Но в данном случае отражена торговая специфика (возможны хищения неучтенных товаров), а гипотеза, которую нужно подтвердить или опровергнуть, взята не с потолка, а из вполне разумных и понятных студентам соображений («регулярная» укладка арбузов в контейнер хотя и не применяется на практике, однако трудно сомневаться в объективности полученного с её помощью значения вместимости).

Ход решения

Объём сплющенного эллипсоида вращения вычисляется по формуле

V = 4/3 π r²h (если сплющивание отсутствует, то r = h )

Ниже будет поясняться случай арбузов шаровой формы, но студенту может быть дано и задание для формы более общего вида.

Обозначим через R1 и R2 радиус арбуза в 10 кг и арбуза в 7 кг соответственно (в сантиметрах). С помощью формулы для объёма шара легко получить, что R1 = 13,37 см и R2 = 11,87 см. Если считать, что количество слоёв средних арбузов и слоёв крупных арбузов одинаково (при этом количество средних арбузов в слое будет несколько больше, чем количество крупных арбузов в слое, и ниже мы учтём это обстоятельство), то для определения количества слоёв надо поделить высоту контейнера (150 см) на сумму 2*(R1+R2). Получаем 2,97 слоя каждого типа. Так как контейнер открыт сверху, то нагруженные в него арбузы могут несколько выступать выше уровня 150 см, что позволяет считать, что в контейнер можно загрузить 3 пары слоёв (а не 2,97 пары). Теперь оценим количество крупных арбузов, которое можно разместить в одном слое методом 6-угольной укладки (см. рис. 1).

На рис. 1 представлен левый нижний угол дна контейнера (вид сверху). Размер дна по горизонтали рис. 1 равен 600 см, а по вертикали – 300 см. Из-за краевых эффектов не очевидно, что 6-угольная укладка лучше, чем, скажем, квадратная. <В связи с этим можно было бы одному студенту дать случай 6-угольной укладки, а другому – квадратной.> Для 6-угольной укладки получаем, что по вертикали рис. 1 помещается 11 крупных шаров (так как 300/(2*13,37) = 11,22). Значит, во второй вертикальной полосе поместится 10 шаров. Грубая оценка общей ширины двух первых вертикальных полос равна

2*R + 1,732*R , что приближенно равно 49,90 см.

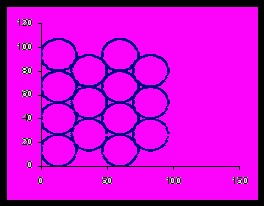
Рис. 1. Левый нижний угол укладки

Так как 600/49,90 = 12,02 , то таких двойных вертикальных полос поместится 12. (Сильному студенту можно дать дополнительное задание: изменится ли этот ответ, если учесть, что вторую «двойную вертикальную полосу» можно намного сместить влево, до соприкосновения с первой). Итого на дне контейнера размещается 21х12 = 252 крупных арбуза.

Что же касается следующего слоя, то возможны два подхода (и, соответственно, две формулировки курсовых работ). Первый подход проще для расчетов, но создаёт неустойчивый тип укладки. В нём арбузы второго слоя (средние по размерам) как бы ставятся на верхние точки первого слоя. Тогда их будет ровно столько же, что и в первом слое (252 штуки). Реально арбузы второго слоя самоуплотнятся как по горизонталям (длина и ширина контейнера), так и по вертикали (высота контейнера). Ведь у них есть возможность заполнить углубления между арбузами первого слоя. Ниже будет взят простейший вариант, в котором «нормальной загрузкой контейнера» будет считатья число 252х6 (так как по высоте помещается три слоя крупных и три слоя мелких арбузов). Это число равно 1512 арбузов.

Далее необходимо сгенерировать 66 разных загрузок контейнера, действительно зафиксированных в предыдущие разы, и затем проверить гипотезу «Арбузы продавались налево». Сделаем стандартное предположение: при исходной загрузке контейнера (и отсутствии хищений) реально загруженное количество арбузов отклоняется от нормативного количества (1512 арбузов) в ту или иную сторону по нормальному закону. Для оценки параметров этого закона (матожидание m и среднее квадратичное отклонение z ) применим стандартные формулы, но в них надо подставлять не все 66 имеющихся данных, а только данные, про которые точно известно, что хищений не было (например, некоррумпированный наблюдатель постоянно сопровождал контейнер от момента загрузки в Астрахани до полной реализации товара в Москве). Для выполнения курсовой примем, что таких «честных» данных имеется только 16 (а остальные 50 находятся под сомнением).

Чтобы студент полностью понял механизм осуществляемой проверки, он должен сам подготовить себе 66 исходных данных для тестирования. Сначала опишем, как готовятся 16 «честных» исходных данных, распределенных по нужному закону. За основу возьмем датчик независимых равномерно распределенных случайных чисел СЛЧИС(), имеющийся в пакете Excel. Числа распределены на отрезке [0,1] и имеют матожидание 0,5 и дисперсию 1/12 . Если рассмотреть сумму 10-и слагаемых такого вида, их закон распределения будет очень похож на нормальный (см. пояснения к заданию № 1). При этом матожидание таких сумм будет равно 10*0,5 = 5 , а дисперсия будет равна 10*(1/12) , так как слагаемые независимы. Нам разумно ориентироваться на числа, у которых матожидание равно 1512, а среднее квадратичное отклонение (то есть корень из дисперсии) равно 70. (Пояснение. Величина с.к.о. зависит от аккуратности грузчиков, загружающих контейнер арбузами. Если бы они строго выполняли правила, по которым рассчитывается нормативное количество арбузов, с.к.о. равнялось бы нулю).

Для преобразования полученных вышеописанным образом случайных чисел, распределенных почти по нормальному закону, к желаемым значениям параметров (1512 и 70) сделаем следующее: вычтем из всех чисел 5 и поделим на корень из 10/12. Получим числа, распределенные по стандартному нормальному закону. Затем умножим числа на 70 и к каждому прибавим 1512. Наконец, округлим полученные числа до целых. Таких чисел нам потребуется 16 («честные» исходные данные).

Аналогичным образом моделируются 50 данных, в которых могли иметь место хищения арбузов. Таких хищений мы «создадим» 10, и они будут случайно разбросаны среди этих 50-и данных. Для целей выполнения курсовой примем, что каждый раз похищалось 200 арбузов, то есть в 10 случаях из 50 надо просто вычесть из сгенерированного случайного числа 200. Данная курсовая не ориентируется на полное изложение методологии выборочных проверок (для более глубокого знакомства см. список литературы со статьями автора), но студенты должны представлять, как она проводится. Например, проверяющий выберет наугад три случая из 50-и, в которых потенциально могут иметь место хищения. С достаточно высокой степенью достоверности один из выбранных случаев попадет на один из 10 случаев, в которых имелись хищения. Тогда стандартная методика проверки гипотезы о том, что матожидание равно 1512 (методом Стьюдента) с 95%-ой надежностью даст ответ, что гипотеза отвергается в пользу того, что матожидание менее 1512 (то есть что хищение в данном случае имело место). В тексте курсовой надо привести только сам процесс вычисления t-переменной Стьюдента и использование таблицы Стьюдента.

Для ориентировки ниже приведены 16 «честных» случайных чисел, сгенерированных вышеописанным способом:

1532 1565 1524 1426 1540 1542 1452 1456

1353 1478 1486 1495 1443 1540 1507 1486

Задание 10 следует рассматривать, скорее,. не как тему отдельной курсовой, а как идеологическую основу для целого семейства курсовых.

Задание 11.

Расчет нелинейной регрессии методом кривых Пирсона

(для тем, связанных с поведением потребителя)

Замечания для преподавателей. С точки зрения маркетинга, речь идет о поведении различных возрастных групп потребителей. С точки зрения эконометрики, речь идет о методе расчета нелинейной кривой регрессии, относящейся к одному из семи типов кривых Пирсона, сглаживающих экспериментальные данные. (См. Сб. задач Л.Д. Мешалкина).

Blog

Пошаговое приближение распределения стоимости покупки к но­р­мальному закону распределения

Постановка задачи

Пошаговое приближение распределения стоимости покупки к нормальному закону распределения