Geum.ru

Пошаговое приближение распределения стоимости покупки к но­р­мальному закону распределения

Вид материалаЗакон
Постановка задачи
Ход решения
Задание 8. Исследование расширения области продаж.
Постановка задачи
Ход решения
Замечания для преподавателей.
Рекомендуется для тем № 27, 30, 18, 11.
Подобный материал:
1   2   3   4   5   6   7   8   9   10   11

Постановка задачи


Оптовик закупает партию из 1000 бутылок сухого вина по исходной цене 100 руб/бут. Он имеет возможность реализовать его либо сразу (по цене 240 руб/бут.), либо через три года (по планируемой цене 320 руб/бут.), либо через 6 лет (по планируемой цене 400 руб/бут.). Допустим, принято решение сделать и то, и другое, и третье в количествах m, n и p бутылок соответст­венно (m + n + p = 1000). Если не принимать во внимание дисконтирование, то выгоднее всего взять m = n = 0, p = 1000 и получить прибыль (400 –100)* 1000 = 300 000 руб. Если ставка дисконтирования в первые три года равна i1, а в следующие три года равна i2, то показатель NPV (net present value), учиты­ваюший изменение ценности денег в зависимости от момента их получения, равен

NPV = –100*1000 + 240*m + 320*n / (1 + i1)3 + 400*p / (1 + i1)3 / (1 + i2)3 .

При больших значениях ставок дисконтирования обесценивание при­были будет настолько боль­шим, что будет выгоднее продать вино ранее, чем через 6 лет.

Осуществить статистическое моделирование значений NPV по ука­занной формуле, задавая i1 и i2 с помощью датчиков случайных чисел (слчис() + слчис())*0,3 и (слчис() + слчис())*0,2 + 0,3 . Привести примеры значений i1, i2 (полученных с помощью вышеприведенных датчиков), при которых вино следует продать ранее 6 лет (полностью или частично).

Ход решения

Генерируются 100 чисел i1 по первой формуле и 100 чисел i2 по вто­рой формуле. Среди них пытаются найти такие, при которых в случае m=n=0 и p=1000 NPV не будет максимальным. Случайные числа, полученные таким образом, имеют симметричный треугольный закон распределения. ВНИМАНИЕ! Вместо слчис() + слчис() нельзя написать просто 2* слчис() !

Задание 8.

Исследование расширения области продаж.


Замечания для преподавателей. Исследование расширения области продаж на примере задачи о торговле пивом в магазине при пивном заводе, находящимися у железнодорожной ветки: имеет ли смысл продавать пиво не только на этой станции, но и на соседних (учитывая, что цена его повысится из-за транспортных расходов), и указать, начиная с каких расстояний это пе­ре­стаёт быть выгодным. Для оценок используется линейная кривая спроса; параметры кривых спроса имеют случайный характер.

Рекомендуется для тем № 5, 20, 24.

Постановка задачи


Напомним понятие «линейная кривая спроса», известное из курса микроэкономики (см. рис. ниже).

Формула кривой спроса связывает между собой цену продажи товара p и количество товара q, которое раскупают потребители при этой цене. (Име­ют­ся в виду потребители, живущие в выбранном регионе, и имеются в виду

покупки, сделанные за данный период времени). Простейшей (линейной) формулой является

p/a + q/b = 1.








В этой формуле a означает «цену отсечки» (начиная с этой цены потребители перестают покупать данный товар), b означает «насыщающее количество» (такое количество потребитель потребил бы, если бы цена на этот товар была ничтожно малой). Отсюда можно выразить q через p (прямая кривая спроса) или p через q (обратная кривая спроса). Линейная кривая спроса удачно сочетает в себе простоту вычислений и сохранение всех экономических особенностей процесса. Например, в данной задаче произво­дитель товара считается монополистом, поэтому он будет назначать цену товара (в данной задаче – пива) такой, чтобы получить максимальную при­быль. Расчеты показывают, что в случае линейной кривой спроса для этого надо назначить цену, равную Pmax = (a + k )/2 (a – цена отсечки, k – стои­мость производства одной еди­ницы товара).

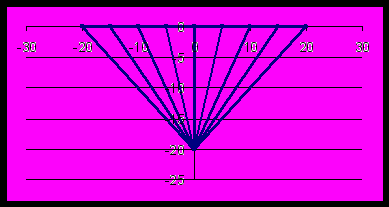
Рассмотрим производителя-монополиста, изготавливающего и реа­лизующего пиво в степной местности в 20 км от железнодорожной линии, на которой имеются равнотстоящие станции с расстоянием 5 км между ними (см. черт.).


На рисунке представлена сеть дорог, идущих из пивного завода к возможным пунктам потребления, находящимся у железнодорожной линии. Так как местность степная, то в любом направлении автотранспорт может ехать по прямой, поэтому все дороги – отрезки прямых. Для пункта потре­бления с координатами (5n, 0) (где n = 0, 1, -1, 2, -2, 3, -3, …) расстояние до пивного завода равно корню из 25n2 + 400. Обозначим это число K(n). Если стоимость производства одного декалитра продукта на пивном заводе составляет s, то в пункте потребления в нее будут включены и транспортные расходы по доставке продукта потребителю, поэтому для потребителя будет назначена цена продажи Pmax = (a + k )/2 , где k равно не s , а s + t K(n) , где t – тариф перевозки 1 декалитра пива на 1 км. Если эта цена превысит цену отсечки, то в данном пункте никто покупать пиво не будет. При расчетах следует считать, что во всех потенциальных пунктах потреб­ления набор пара­метров (a, b) одинаков. Поэтому и цена отсечки везде одинакова. Это рас­-


суж­дение позволяет рассчитать, в какие пункты пиво везти выгодно, а в какие – нет (из-за высоких транспортных расходов).

Далее в каждом из рассчитанных пунктов продажи вычисляется при­быль монополиста, так как из линейной кривой спроса можно определить раскупаемое количество, а значит, и выручку. От нее надо отнять издержки, равные q*( s + t K(n)). Получим прибыль в данном пункте потребления. Ее надо просуммировать по всем пунктам. Зафиксируем b, тогда суммарная при­быль будет зависеть только от выбора s, t, a. Выполняющий задание сту­дент должен сам выбрать разумные значения s, t. Затем надо осуществить стати­сти­ческое моделирование этой ситуации. Для этого генерируются сто значе­ний цены отсечки a и для каждого вычисляется прибыль с учетом того, что количество пунктов потребления может изменяться. Из-за этого прибыль может совершать скачки, хотя цена отсечки может расти (или убывать) непре­рывно.


Ход решения

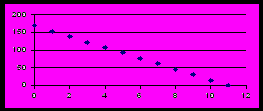
Для генерации случайных значений цены отсечки можно использо­вать формулу типа 20+5*слчис(). По этой формуле получаются случайные числа, равномерно распределенные по отрезку [ 20; 25]. Для каждого из случайных чисел выяснить, в какие именно пункты выгодно везти пиво, и какова будет суммарная прибыль. Желательно построить две столбцовых диа­граммы: значения цены отсечки и соответствующие им значения прибыли.


Задание 9.

Множественная регрессия и особенности её использования для изучения рынка офисов в Москве

Замечания для преподавателей. Регрессия такого типа обычно рас­счи­тывается по 40-50 исходным данным, отвечающим ограничению «при прочих равных условиях». В качестве регрессоров для жилых квартир используются рас­стояние до бли­жай­шего метро, экология района, этажность (и этаж проживания), раздель­ность санузла, пло­щадь кухни. Данные регу­лярно публикуются риэлторскими фирмами, но проблема заключается в том, что 40-50 исходных данных слиш­ком мало, чтобы регрессоры «почув­ствовали» особенности ситуации и позво­лили тем самым найти правильные и пригодные для практики коэффициенты регрессии. В данном задании вместо истинных данных о продаже квартир создан «артефакт», пригодный только для учебного упражне­ния (количество данных, использованное для расчета, не выдерживает никакой критики и равно одиннад­цати). Вместо квартир взяты офисы, состоящие из нескольких зданий, нескольких входов, разной площади и разного срока эксплуатации (среди которых есть даже срок в 99 лет). Несмотря на такие карикатурные исходные данные, расчет регрессии хорошо защищен от нападений критиков, так как большинство статис­тических проверок она проходит успешно. Сту­дент должен оценить пригодность рассчитанной модели для практического применения (испо­льзовать, в частности, многомерный показатель R2 ).

Рекомендуется для тем № 27, 30, 18, 11.