Пошаговое приближение распределения стоимости покупки к нормальному закону распределения
| Вид материала | Закон |
- Лабораторная работа 1-08 экспериментальное изучение гауссовского закона распределения, 108.63kb.
- Дискретные случайные величины Ряд распределения, 29.73kb.
- Природа каналов распределения товаров. Их структура и управление, 20.88kb.
- Лабораторная работа №2 Тема: Формирование выборки случайных чисел, распределенных, 151.75kb.
- Функция распределения. Плотность распределения. Основные параметры непрерывных случайных, 7.05kb.
- Законом распределения, 13.27kb.
- Методы и каналы распределения товаров, 82.28kb.
- Лекция 10. Управление системой распределения >10. Управление системой распределения, 258.27kb.
- Задача оптимизации расположения распределительного центра на обслуживаемой территории, 872.4kb.
- Секция №1 Модераторы: В. Стрельченок, Е. Толстая, И. Ратанова, 183.54kb.
Ход решения
Чтобы рассчитываемая регрессия была более близкой к реальным данным, приведем некоторые сведения об урожайности картофеля и об увлажненности почвы и содержании в ней перегноя. На сайте «Китай в цифрах имеются следующие сведения об урожайности картофеля за несколько лет (в центнерах с гектара):
Год Урожайность картофеля
1980 112.45
1985 108.02
1990 113.21
1995 133.84
2000 140.35
2005 167.62
Для сравнения даны урожайности других стран:
Австрия 319.27
Люксембург 319.11
Швеция 311.06
Канада 293.94
Для измерения влажности используется понятие «полевой влагоёмкости» (естественная способность почвы удерживать воду). Цитируем отрывок с сайта www.mygarden.ru .
«Отличная степень влажности при 75 — 100% полевой влагоемкости. О ней можно судить по тому, что почва скатывается в прочный комок, очень податлива при сдавливании, легко слипается. Если почву сдавить сильнее, к пальцам прилипнет довольно большой комочек. И совсем плохо, если почва слишком влажная, выше полевой влагоемкости, когда при сильном сжатии из комка можно выжать немного воды. Поливать при таком ее состоянии не только расточительно, но даже вредно».
Будем задавать влажность в процентах от полевой влагоёмкости, в диапазонах от 10% (недостаточное увлажнение) до 80% (отличное увлажнение).
Содержание в почве перегноя (гумуса) будем изменять в пределах от 6% (подзол) до 15% (чернозем). Чтобы отразить факт истощения почвы (в упрощённой форме), в каждом следующем году и нижнюю, и верхнюю границу будем уменьшать на 1%.
Отметим, что строить парную регрессию по приведенным выше данным урожайности в Китае хотя и можно (с точки зрения математики), но не имеет особого смысла, так как со временем почва истощается, и нельзя считать. что дисперсии регрессионных остатков постоянны. (Здесь скорее помог бы анализ временных рядов).
Хотя количество делянок равно 400, мы будем выбирать только 100 из них (выбор можно делать случайным либо регулярным образом). Множественную регрессию ищем в виде (х – влага, у – перегной, z – урожайность):
z = A x + B y + C
Представим участок графически (вид сверху):
перегной
0 0 0 1 0 1 0 0 1 0 1 0 0 1 0 0 1 0 0 0
0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 1 0 1 0 1 1 0 0 0 1 0 0
0 0 1 1 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 1
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 1 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0
1 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0
0 0 1 0 1 0 1 1 0 1 0 1 0 0 1 0 0 0 1 0
1 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0 1 0 0 0
0 0 0 0 1 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0
0 1 0 1 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 0 0 0
1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 1 1 0 0 0
1 0 0 0 0 0 1 1 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0
0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 1 0 0 0 0
нач. отсчета влажность
На схеме представлены 400 делянок, помеченных нулями и единицами (единицы означают, что данные с этой делянки будут учтены в расчете регрессии). Единицы были сгенерированы по формуле
Если(СЛЧИС()<0,25;1;0)
Теоретически говоря, вероятность появления единицы в этой формуле равна 0,25. Однако практически единиц оказалось не 100, а только 75. Однако этого количества достаточно для грамотного построения регрессии (наглядно видно, что единицы равномерно покрывают поле). Влажность будем откладывать по горизонтали, содержание перегноя – по вертикали. На делянке в левом нижнем углу влажность и содержание перегноя минимальны (10% и 6%), а в правом верхнем углу – максимальны (80% и 15%). Если условно принять, что на каждой делянке замеры влажности и перегноя делаются именно в левом нижнем углу, то нарастание влажности выражается формулой В = 10 + 70*х/(1000 – 50), где х – абсцисса левого края делянки. В самом деле, для первой делянки в горизонтальном ряду х=0, а В = 10 (процентов). А для последней делянки х=950 (метров), В = 80. Аналогичным образом, нарастание перегноя в почве выразится формулой П = 6 + 9*у/(1000 – 50), где у – ордината нижнего края делянки.
Теперь нам понадобятся сведения об урожайности на делянках, помеченных единицами. Так как реальных данных у нас нет, для объяснения методики расчёта осуществим генерацию урожайности искусственным образом,
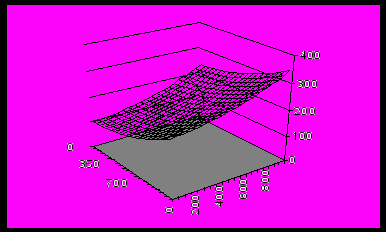
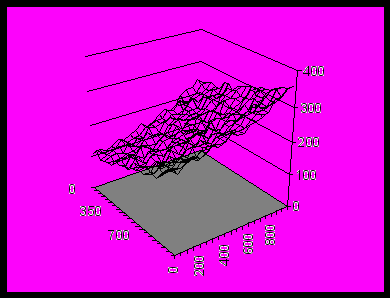
Рис.6. Поверхность урожайности картофеля, смоделированная
с учетом случайных возмущений.
считая, что она ориентировочно лежит в пределах от 170 до 310 (центнеров с гектара; см. реальные данные, приведенные выше). За основу возьмем зависимость вида z = ((x /1000 - 0,1)2 + (y/1000 – 0,2)2)*100 + 100 (смещенный параболоид вращения), график которого привелен перед рис. 6.
Из графика видно, что нелинейность этой поверхности на данной области значений (х,у) слабая, так что вполне уместно будет приближённо изобразить её плоскостью (плоскость регрессии). Значения же z дают правильные с экономической точки зрения значения урожайности картофеля: в точке (0,0) с неблагоприятным сочетанием объясняющих переменных урожайность невелика (около 100 цент./га), а в точке (950,950) с высокими влажностью и содержанием перегноя она высокая (примерно 340 цент./га). Кроме того, в реальной жизненной практике зависимость урожайности от влажности и количества перегноя и в самом деле будет слабо нелинейной (хотя, конечно, вовсе не обязательно эту поверхность можно представить как параболоид вращения). Осталось «запылить» эту поверхность случайными отклонениями, для чего можно прибавить в каждой точке случайное число по формуле СЛЧИС()*30. Результат прибавления представлен на рис. 6. Поверхность имеет характерный вид «скомканной бумаги». Теперь можно приступать к расчету регрессии.
Чтобы рассчитать регрессию, отражающую поведение этих данных рассматриваемых как экспериментальные данные замеров на делянках, надо обычным образом выписать таблицу из трех столбцов и 75-й строки (напомним, что из 400 делянок мы случайным образом выбрали 75 делянок). В первом столбце мы запишем известные значения объясняемой переменной (то есть урожайности), а во втором и третьем столбце – значения объясняющих переменных (влажность, содержание перегноя). Так как в регрессию входит и постоянное слагаемое, то можно было бы записать ещё и третий столбец (состоящий из единиц), но он будет дописан самим компьютером, если задать нужный режим расчёта.
Однако в этом месте возникает чисто техническая трудность: данные надо расположить по столбцам, а в исходный момент они будут записаны внутри матрицы. Изложим удобную компьютерную процедуру преобразования матрицы в столбец. Если матрица имеет размеры 20 на 20 и состоит из чисел a i j , то вектор имеет 400 компонент b k , вычисляемых по формуле (в случае считывания элементов матрицы по столбцам):
k = i + 20*(j – 1)
Для реализации такого рода формул в Excel используем короткую программу на языке Visual Basic:
For j = 1 To 3
For i = 1 To 2
Cells(i + (j - 1) * 2, 5) = Cells(i, j)
Next
Next
Под действием этой программы матрица 2х3, записанная в левом верхнем углу таблицы Excel , переписывается по столбцам в пятый столбец, то есть столбец Е.
Любые другие варианты переписывания матрицы по столбцам легко получить видоизменением этого текста (являющегося макросом для электронной таблицы Excel). Укажем попутно, как без лишнего формализма внедрить макрос в Excel-таблицу:
1) запускаем режим Сервис, Макрос, Начать запись. Переход в режим записи подтверждается появлением в таблице маленького окна, в котором указана синяя кнопка (нажатие на которую приводит к остановке записи). Предварительно надо задать имя макроса и комбинацию клавишей для его вызова (например, Ctrl-h).
2) Делаем в режиме записи некоторое действие (например, закрашиваем красным выделенную курсором ячейку) и щёлкаем мышью на кнопке останова.
3) Входим в режим Сервис, Макрос, Макросы, Изменить. На экране появляется текст макроса, только что записанного нами. Добавляем к нему (без ошибок!) указанный выше (но видоизмененный для данной ситуации) текст с двойным циклом.
4) закрываем окна отладчика Visual Basic и запускаем в появившейся после этого Excel-таблице нужный нам макрос комбинацией Ctrl-h.
Ниже показано, как был изменен текст макроса для расчета столбцов нашей регрессии (речь пока идёт о столбцах длины 400; далее они будут сокращены до длины 75). Результат записывается в столбце W начиная с 46-го места).
For j = 2 To 21
For i = 48 To 67
Cells(i - 2 + (j - 1 - 1) * 20, 23) = Cells(i, j)
Next
Next
Прежде, чем применять этот макрос, необходимо заполнить нулями таблицу 20х20, где вычислены 400 значений урожайности, на тех местах, которые не попали в выборку из 75 делянок. Для вычисления урожайности использовалась формула
((B$24/1000+0,1)2+($A25/1000+0,2)2)*100+100+СЛЧИС()*30
Копирование этой формулы вправо и вниз (с учётом расставленных в ней знаков доллара) и даёт 400 значений урожайности. За основу взята слабо искривленная поверхность, и её значения искажены добавлением случайных чисел в диапазоне от 0 до 30. Вместо формул введены их значения, иначе эта матрица будет изменяться с каждым шагом работы Excel.
Затем значения этой формулы копируются на свободное место Excel-таблицы. На том же листе таблицы уже записана таблица из нулей и единиц, показывающая, какие делянки попали в выборку. При копировании следует применить команду вида Если(В25=0;0;В25). Тогда значения урожайности будут даны только в выбранных 75 точках, а на остальных местах получатся нули.
По аналогичной методике получаются и два столбца (длины 400) со значениями двух объясняющих переменных. В одном из них записаны влажности В (зависят от х), в другом – содержания перегноя П (зависят от у). Формулы для них приведены выше.
Для отделения ненулевых чисел в полученных трех столбцах от нулевых надо выделить все три столбца вместе и отсортировать по убыванию любой из трех столбцов (вместе с ним синхронно будут сортироваться и соседние два столбца). В итоге нули окажутся в самом конце, но при этом порядок данных регрессии (75 чисел) изменится. Как известно, коэффициенты регрессии от такого изменения не меняются.
Окончательно 75 исходных данных для расчета урожайности Z по влажности почвы X и содержания в ней перегноя Y приведены ниже в виде таблицы, имеющей четыре столбца (№ п/п, Z, X, Y) и 75 строк. Для удобства расположения на странице эта таблица разбита на три порции по 25 чисел.
1 332 65,3 15 26 227 76,3 8,37 51 181 54,2 6,5
2 323 80 14,1 27 226 72,6 8,37 52 181 17,4 11
3 315 65,3 14,5 28 225 72,6 6,47 53 179 57,9 6
4 315 61,6 14,5 29 220 61,6 9,32 54 179 24,7 12
5 301 54,2 15 30 219 50,5 10,7 55 173 28,4 9,8
6 289 68,9 13,6 31 217 54,2 10,3 56 171 46,8 6,9
7 285 65,3 13,6 32 215 61,6 10,7 57 170 35,8 9,3
8 279 68,9 12,2 33 213 72,6 7,89 58 169 46,8 7,9
9 274 39,5 15 34 210 50,5 11,2 59 168 39,5 7,9
10 267 72,6 12,2 35 210 10 13,6 60 165 54,2 7,9
11 264 57,9 13,1 36 208 13,7 13,6 61 164 24,7 11
12 261 61,6 12,6 37 208 46,8 11,2 62 161 32,1 8,4
13 260 80 8,84 38 208 43,2 10,7 63 160 21,1 10
14 256 76,3 10,7 39 203 39,5 11,2 64 157 17,4 9,3
15 254 21,1 14,5 40 197 68,9 6 65 157 10 9,8
16 251 68,9 11,7 41 194 13,7 12,2 66 152 21,1 8,4
17 246 68,9 11,2 42 193 32,1 10,7 67 151 39,5 6
18 244 50,5 13,1 43 193 35,8 10,7 68 151 46,8 6
19 244 43,2 13,6 44 193 32,1 11,7 69 150 39,5 7,4
20 243 35,8 14,1 45 193 39,5 10,3 70 150 17,4 8,4
21 241 21,1 15 46 190 57,9 7,89 71 149 32,1 8,8
22 240 80 8,37 47 189 21,1 12,2 72 134 28,4 6
23 238 65,3 10,3 48 189 28,4 12,2 73 132 28,4 6,5
24 232 10 14,1 49 188 50,5 9,79 74 118 21,1 6
25 231 32,1 14,1 50 186 10 11,2 75 116 24,7 6,5
В этой таблице значения урожайности расположены по убыванию, но конкретный порядок следования данных для расчета регрессии роли не играет.
Для расчета коэффициентов регрессии используем стандартную процедуру Excel для расчета множественной линейной регрессии:
ЛИНЕЙН(A1:A75;B1:C75;1;1)
Точки с запятой отделяют друг от друга следующие начальные данные и установки: набор объясняемых переменных; набор пар объясняющих переменных, учесть постоянное слагаемое; рассчитать статистику регрессии. Так как массивы имеют большой объём, сделаем тестирование работы этой процедуры на малом объеме исходных данных и на известном заранее ответе. В роли теста возьмем плоскость регрессии z=7x+8y+9 и будем восстанавливать эту плоскость по следующим данным:
Z X Y
40,05 1 3
78 3 6
69 4 4
54 3 3
Первое значение Z в идеальном случае должно равняться 40, но мы его немного исказили (иначе при расчете статистике получится деление на нуль). Получен ответ для теста:
7,997449 6,983 9,0704
0,0066718 0,007 0,028
0,9999997 0,015 #Н/Д
1826560,3 1 #Н/Д
838,72665 2E-04 #Н/Д
В первой строке идут коэффициенты, близкие к числам 8, 7, 9. Отсюда делаем два вывода: а) процедура дала верный ответ, так как с самого начала мы знали, что верный ответ будет близок к числам 7, 8, 9; б) процедура ЛИНЕЙН устроена так, что коэффициенты рассчитанной регрессии выдаются в следующем порядке: на последнем месте – свободное слагаемое, а коэффициенты при объясняющих переменных идут в обратном порядке по отношению к порядку следования столбцов исходных данных. Третье число в первом столбце дает коэффициент детерминации R2 . Его значение получилось столь близким к единице благодаря малому отличию тестового значения Z=40,05 от идеального значения 40. Действуя аналогичным образом для основного варианта расчета, получаем ответ:
14,148428 1,529 -6,628
0,5376008 0,071 6,7454
0,938929 12,57 #Н/Д
553,47811 72 #Н/Д
174825,75 11371 #Н/Д
#Н/Д #Н/Д #Н/Д
Пользуясь первой строкой, получаем ответ:
Z = 1,529 X + 14,15 Y – 6,63
Первые два коэффициента положительны, что соответствует экономической сути задачи: с ростом увлажнения и с ростом содержания перегноя урожайность тоже нарастает. Третий коэффициент экономического смысла не имеет и позволяет только повысить точность регрессии. Поэтому его отрицательность не является свидетельством неправильности расчета.
Количество степеней свободы равно 72, так как, найдя значения оценок трех коэффициентов регрессии, мы связали 75 исходных данных тремя линейными уравнениями. Остаточная сумма квадратов равна 11371. Этот ответ, зная коэффициенты регрессии, легко проверить. <Студентам рекомендуется включить эту проверку в текст курсовой>.
Имея уравнение регрессии, можно решить ряд практически важных экономических задач. Например, вычисляя значения регрессии на каждой из 400 делянок, можно найти прогноз общего урожая, полученного с этого поля в следующем году. Более того, можно с помощью той же регрессии сделать прогноз урожая на 2,3, 4 и 5 лет вперёд, если значения «у» сместить на нужное расстояние вниз. Тем самым будет учтено постепеноое уменьшение количества перегноя в почве после снятия очередного урожая.
В курсовой работе это необходимо проделать и сложить пять полученных прогнозов величины урожая картофеля. Следует также построить график найденной регрессии в виде плоской поверхности.
Задание 16.
Изучение устойчивости регрессионной прямой при засорении исходных данных случайными ошибками с нарастающей дисперсией
Для преподавателей. Расчет регрессии по классической формуле в случае гетероскедастичности ошибок является, как известно, некорректной операцией. Однако в данной курсовой речь будет идти не об использовании на практике неверно сделанного расчета, а о сравнении большого количества неверно сделанных расчетов (в достаточно большом количестве точек, а именно, в десяти) с верным решением, чтобы найти величину допущенной ошибки. Такое задание поможет понять студенту суть возникающих в этом случае трудностей и развить интуитивное восприятие регрессии.
Постановка задачи
Инновационная фирма «Авто-Водород» объявила о широких продажах через10 месяцев нового типа автомобилей с водородным двигателем. Пробные образцы их будут продаваться в начале каждого из 10 месяцев, оставшихся до начала массовых продаж. Специалисты фирмы считают, что при отсутствии интенсивного рекламного воздействия на покупателей количества пробных закупок нарастали бы по линейному закону, так как новые двигатели действительно лучше бензиновых. Однако в обществе имеются две противоположных тенденции лоббирования, публикующие тенденциозные материалы о новых автомобилях как в сторону преувеличения их достоинств (заголовки «Водород – путь вперёд», «Долой бензиновых чудовищ», «Конец отраве выхлопными газами» и т.д.), так и в сторону нагнетания страха перед непривычной техникой (заголовки типа «Растёт число погибших от взрыва водорода», «Трагедия в цеху фирмы «Авто-Водород»», «Пора запретить недоработанную конструкцию»). По мере приближения момента массового появления водородных автомобилей на рынке воздействия печатных и телевизионных материалов на поведение покупателей усиливаются, так как в перспективе одна группа производителей останется не у дел, а другая – получит крупные прибыли. Это воздействие носит случайный характер, так как одному покупателю попадается на глаза хвалебная статья, а другому – разгромная. Из-за этого кривая продаж носит не линейно-нарастающий характер, а скачкообразный, причем размах скачков усиливается по мере движения от 1-го месяца к десятому.
Осуществить статистическое моделирование ситуации, подготовив 30 наборов по 10 данных в каждом, показывающих купленное количество новых автомобилей в начале каждого из 10 месяцев предварительной продажи. Это количество генерируется на компьютере как сумма двух слагаемых, одно из которых линейно нарастает от 700 до 1600 покупок, а второе является случайной величиной, распределенной по нормальному закону с нулевым средним значением и со значением с.к.о., линейно нарастающим от 20 до 65 автомобилей по мере увеличения номера месяца.
По каждому из тридцати наборов по 10 чисел рассчитать прямую регрессии и все их изобразить на одном чертеже. На том же чертеже изобразить жирной линией линейную функцию, которая имела бы место, если бы рекламное воздействие на потребителей отсутствовало бы. Сделать вывод, можно ли было бы «угадать» эту объективную линию среди тридцати тенденциозных реализаций.
Ход решения
Для пояснения вместо 30 наборов будут обработаны только 5. Прочее студент завершает самостоятельно.
Как обычно, запишем линейную формулу для вычисления продаж согласно объективной линии: y = 700 + 100*(n – 1), где n - номер месяца. Укажем также линейный закон нарастания с.к.о : z = 20 + 5*(n – 1).
Как уже было сделано в одной из предыдущих курсовых, для моделирования случайных чисел, распределенных по нормальному закону, возьмём сумму двенадцати слагаемых вида 2*СЛЧИС()-1. Ниже приведен образец моделирования 30-и таких чисел:
-1,71 3,76 1,63 -5,54 3,20 0,42 0,08 -1,25 -2,61 -1,99
-2,88 1,37 -0,49 2,26 3,31 -0,50 0,74 0,58 -1,46 2,55
-2,44 -1,31 -2,40 2,27 -4,77 2,34 3,05 0,22 0,64 -2,71
Каждое из 12 независимых слагаемых имеет матожидание, равное нулю, и дисперсию, равную 4*(1/12). Поэтому их сумма имеет дисперсию, равную четырём. (Проверка по несмещенной оценке дисперсии дает 4,156). Деля числа пополам, получаем выборку из стандартного распределения N(0,1). Подготовим десять таких выборок (по одной на каждый месяц продаж). Сведём эти выборки в матрицу 30х10. Столбцы матрицы умножим на нужное значение с.к.о. (нарастающее от 20 до 65). К каждой строке матрицы прибавим линейный тренд от 700 до 1600. Получим 30 экземпляров значений объясняющей переменной (номер месяца) для расчета прямых парной регрессии (с учётом постоянного слагаемого). Ниже приведены первые 5 из этих строк.
658 835 907 1022 1043 1166 1222 1404 1428 1506
721 858 890 988 1055 1209 1357 1400 1462 1547
681 802 921 1024 1103 1224 1301 1502 1432 1583
715 776 912 1014 1053 1214 1271 1456 1528 1489
702 767 937 1043 1007 1235 1263 1357 1556 1605
Расчет регрессий по этим данным даёт пять ответов:
90,85455 619,4 #Н/Д 93,77576 632,9333 #Н/Д
4,192102 26,01131 #Н/Д 3,97796 24,6826 #Н/Д
0,983253 38,07666 #Н/Д 0,985809 36,13162 #Н/Д
469,7098 8 #Н/Д 555,7254 8 #Н/Д
681000,2 11598,65 #Н/Д , 725496,1 10443,95 #Н/Д ,
99,30303 611,1333 #Н/Д 96,25455 613,4 #Н/Д
5,032022 31,22288 #Н/Д 5,358688 33,24978 #Н/Д
0,979871 45,70561 #Н/Д 0,975805 48,6727 #Н/Д
389,4394 8 #Н/Д 322,6455 8 #Н/Д
813540,1 16712,02 #Н/Д , 764357,3 18952,25 #Н/Д ,
100,8364 592,6 #Н/Д
5,563394 34,51995 #Н/Д
0,976227 50,53203 #Н/Д
328,5147 8 #Н/Д
838857,7 20427,89 #Н/Д .
Таким образом, вычислены регрессии y = 90,85 x + 619,
y = 93,77 x + 633, y = 99,30 x + 611, y = 96,25 x + 613,
y = 100,83 x + 593.
На рисунке даны пять линий регрессии. Они отличаются слабо, поэтому рекламные усилия не приводят к затемнению сути дела.
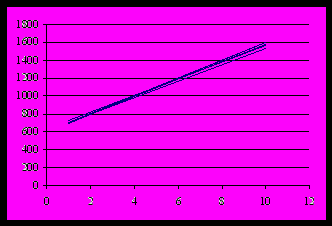
Когда будут изображены на одном чертеже все тридцать реализаций, придётся обдумать вопрос о повышении разборчивости этого чертежа (показ только центральной части, укрупнение масштаба и т.д.). Иначе трудно будет сравнивать невозмущённую прямую регрессии с возмущёнными. Эта задача решается студентом без помощи преподавателя.
Задание 17.
Статистические методы пополнения недостающих рыночных данных
Постановка задачи
Социальный работник делает недельную закупку продуктов на рынке для семьи пенсионеров. Обычно он сразу записывает количество и стоимость приобретенных продуктов, но иногда он закупает их сразу несколько, а затем вспоминает лишь общую стоимость (а объём закупок он восстанвливает по листку заказа). Работник имеет представление о том, каковы должны быть, примерно, цены на закупаемые продукты на этом рынке, но от этих данных возможны случайные отклонения, распределенные по нормальному закону. Закупленная в одном месте группа продуктов может состоять как из однотипных продуктов, так и совершенно разных, но продаваемых в соседних торговых точках. Разработать алгоритм наиболее правдоподобного восстановления
забытых денежных стоимостей.
Типовые примеры закупок, делаемых социальным работником
| Траты 21.10.07 (вс) | Рублей |
| фарш говяжий 1 кг | 132 |
| сыр "Маасдам" 0,65 кг | 115 |
| сыр с паприкой 200 г | 52 |
| рыбн. диски-филе 1,6 кг | 216 |
| мор.окунь (две шт.) | 142 |
| чавыча 1 шт. | 108 |
| тыква кусок | 20 |
| капуста+лук | 50 |
| баклажаны + перец + помид. | 90 |
| виноград+(груши 1 кг) | 95 |
| грейпфруты 2 шт. | 27 |
| гранат 1 шт. | 29 |
| перчатки мужские | 50 |
| чеснок 3 голов. | 15 |
| скумбрия г/к 1 шт. | 90 |
| кефир 0,5 л | 22 |
| хлеб бородин. 0,5 кг | 7 |
| творог с изюмом 300 г | 21 |
| чай черн. "Ахмат" | 42 |
| котлеты из цыпл. 2 шт. | 16 |
| курага 0,5 кг | 40 |
| стир.порошок "Ариэль" | 46 |
| творог 400 г+смет.+ слив. масло | 148 |
| торт йогурт. | 223 |
| вино полусл. | 160 |
| ИТОГО рублей | 1956 |
Анализ данных показывает, что в этом списке три раза была записана не отдельная стоимость продукта, а сумма двух-трёх стоимостей. За основу взяты реальные данные о ценах на Преображенском рынке г. Москвы. Так как закупка продуктов повторялась много раз, то можно получить статистические данные о параметрах распределения цен (они считаются распределенными понормальному закону). Ниже приведён ещё один пример.
| Траты 28.10.07 (вс) | Рублей |
| фарш говяжий 1,1 кг + бёдрышки | 197 |
| сыр "Ренессанс" 0,7 кг | 184 |
| сыр углич. с паприкой 460 г | 115 |
| рыбн. диски-филе 6 шт. | 106 |
| мор.окунь по 115 р. | 40 |
| скумбрия г/к 1 шт. | 106 |
| смет.+сливоч. масло (170р/кг) | 150 |
| хвост сёмги большой | 253 |
| капуст.кваш. 1 кг | 50 |
| помидоры | 40 |
| масло нерафин. | 50 |
| яйца 1 кат. | 34 |
| виногр."тойфи" >1 кг | 70 |
| гранат 2 шт. | 50 |
| черн. редька | 6 |
| картофель 5х13р. | 65 |
| леденцы "Бон Пари" | 19 |
| лук | 10 |
| нутрян жир 200 г | 37 |
| кефир | 28 |
| молоко | 38 |
| сливки 10% | 20 |
| творог 5% | 22 |
| Плав.сырки "Виола" | 35 |
| Творож. сырки по 12,5 р. | 37 |
ИТОГО рублей | 1762 |
Следует пояснить, почему цены на пищевые продукты следует считать случайными величинами, даже если их кто-то и зафиксирует в приказном порядке. Дело в том, что продукты могут иметь разное качество, то есть и разную потребительскую ценность. Стандартизировать продукты (как это делается, например, на биржах, торгующих зерном), очень трудно. Например, сливочное масло домашнего производства продаётся в виде цилиндрических кусков, расфасованных в полиэтиленовые паветы. Куски продаются только целиком, и взвешивание производится только в момент продажи. Покупатель просто осматривает товар и выбирает кусок, который ему приглянулся. Если ему нужен был кусок в 300 г, по цене 170 руб/кг, и выбранный кусок ему подходит, то он не будет возражать, если его цена окажется не 51 рубль, как он ожидал, а 48, 54 или 55 рублей, так как вес его немного отличался от трёхсот грамм, желаемых покупателем. Но это как раз и равносильно тому, что разные покупатели покупают масло по разной фактической цене (остающейся близкой к 170 руб/кг). То же относится к продаже арбузов, апельсинов , сырого мяса и т.п. Поскольку количество закупок велико, по типовым товарам (говяжий фарш, копчёная рыба и т.д. ) можно получить представительную выборку реальных продажных цен, тщательно замеряя в домашних условиях точный вес купленного товара и сравнивая его с тем, который желал получить покупатель. Это и позволит от объявленной продавцом цены товара перейти к реальной цене, по которой совершилась покупка. Следует также отметить, что даже если и цена, и вес соблюдены правильно, есть ещё возможность различных вариаций за счет качества товара, которое проверить очень затруднительно (выдержка сухого вина, крупность куриных яиц, «диетичность» яиц, мясо 1-й и 2-й категории и прочее).
Сформулируем один из возможных конкретных вариантов данной курсовой работы и на нём поясним порядок её выполнения.
Каждое воскресенье на рынке закупается набор пищевых продуктов определенного вида, количесто (вес) которых определяются заранее, а цена покупки является случайной величиной нормального типа, параметры которой (м.о. и с.к.о.) не меняются в течение рассматриваемого периода и известны заранее. (Эти случайные величины должны быть смоделированы студентом на компьютере). В нормальной ситуации социальный работник, делая покупку, тут же записывает вид товара, количество и уплаченную за него сумму. Но иногда приходится закупать несколько продуктов сразу (например, овощи), и работник помнит только общую уплаченную сумму. В плане закупок у него записано, что данного продукта надо закупить, скажем, 400 г. Но реально вместо 400 г могло получиться 435 г (небольшое отличие от запланированного). Как указано выше, можно считать, что закуплено всё-таки 400 г, но по более высокой цене. Например, допустим,что закуплены сразу 323 г мёда по 160 руб/кг (вместо заказанных 300 г), два десятка яиц по 22 рубля (вместо ориентировочной цены 20 руб/десяток), 480 г сливочного масла по 170/руб/кг (вместо желаемых 500 г) и баночка сметаны в 255 г по 130 руб/кг (вместо ориентировочных 250 граммов). Итого уплачено
0,323*160 + 2*22 + 0,48*170 + 0,255*130 = 210,43 рубля.
В расход было записано 211 рублей, а точные веса и цены товаров были забыты. Поэтому при анализе покупок придётся решать уравнение с четырьмя неизвестными 0,3*x + 2*y + 0,5*z + 0,25*u = 211, где
x – забытая цена мёда (при правильном решении задачи она должна оказаться близкой к 160)
y – цена продажи десятка яиц,
z – цена сливочного масла
u – цена 1 кг сметаны.
В обычной ситуации для решения задачи потребовалось бы ещё три уравнения. Трудно надеяться, что такие уравнения удастся составить в пределах одного и того же дня закупки (один и тот же продукт не закупается в разных местах рынка). Однако имеется много аналогичных уравнений по итогам других дней закупки, и в них вполне может входить сливочное масло того же вида. Но в этих уравнениях может оказаться другое количество товара, а главное – набор товаров может быть другим (например, мёд, масло сливочное, масло подсолнечное, рыба копчёная, фарш говяжий). Тогда придётся включить в рассмотрение другие неизвестные и другие уравнения (уравнений заведомо будет больше, так как список продуктов ограничен, а количество закупочных дней достаточно велико). Ниже будет рассмотрено только 4 неизвестных (x, y, z, u) и шесть уравнений
0,3*x + 2*y + 0,5*z + 0,25*u = 211,
0,2*x + 1*y + 0,5*z + 0,45*u = 199,
0,3*x + 0,5*z + 0,27*u = 171,
0,33*x 0,5*z = 142,
0,4*x + 3*y + 1,5*z + 0,29*u = 415,
1*x + 2*z = 502..
В первом уравнении правая часть оставлена прежней (211 рублей), а левая часть изменилась, так как вместо истинных весов продуктов теперь указаны запланированные веса.
Как известно, для решения такого рода систем уравнений (в которых количество линейных уравнений больше количества неизвестных) применяется метод наименьших квадратов. С помощью его добиваются того, чтобы левые части были не точно, а приближенно равны правым, причём сумма квадратов разностей левых и правых частей была бы минимальной.
Ход решения
После беседы с преподавателем выбрать нужное количество неизвестных (то есть цен, которые надо восстановить) и количество уравнений, включающих эти цены (уравнений должно быть больше, чем неизвестных). Задать матожидания всех неизвестных (то есть типовые цены на продукты в 2007/08 годах), и их с.к.о. (для ориентировки использовать приведенные выше реальные данные). Смоделировать для каждого из уравнений числовые значения неизвестных, распределенные по нормальному закону с выбранными значениями м.о. и с.к.о. Значения моделируются тем же методом суммирования 12-и чисел, отвечающих формуле 2*СЛЧИС()-1, который изложен в изложенных ранее заданиях.
Умножая коэффициенты каждого уравнения (их надо подобрать так, чтобы матрица коэффициентов была невырожденной) на смоделированные значения неизвестных, получаем правые части уравнений.
Пример. Для рассмотренной выше системы 6 уравнений с четырьмя неизвестными правые части равны 211, 199, 171, 142, 415, 502.
Решение такой системы методом наименьших квадратов равносильно расчету множественной линейной регрессии без постоянного слагаемого. В роли объясняемого вектора выступают правые части уравнений, а в роли объясняющих векторов выступают коэффициенты при x, y, z, u.
Выполняя команду ЛИНЕЙН с нулем на предпоследнем месте, получаем ответ:
134,8627 156,4 21,802 189,6 0
2,595277 2,174 0,5989 4,341 #Н/Д
0,99998 1,052 #Н/Д #Н/Д #Н/Д
24682,88 2 #Н/Д #Н/Д #Н/Д
109363,3 2,215 #Н/Д #Н/Д #Н/Д
Из этих данных (читая первую строку справа налево) мы получаем, что цена меда получилась равной 189,6 руб. (вместо 160), цена десятка яиц 21,8 руб. (вместо 20), цена сливочного масла 156,4 руб. (вместо 170) и цена сметаны 134,9 руб. (вместо 130).
Задание 18.
Подготовка различных вариантов задания для расчета себестоимости женских сапог методом множественной регрессии
Пояснение для преподавателей. Задача о себестоимости женских сапог регулярно включалась автором в начальный курс эконометрики, читаемый в РЭА на факультетах ОЭФ, БИДА, Маркетинга, Финансовом. Основной целью этой работы было освоение техники расчета регрессии на примере задачи, имеющей ясный экономический смысл. Поэтому вариант был у всех студентов одинаковый, но с каждым из них при защите работы производилась персональная беседа. В конце семестра возрастал поток студентов, которые быстро списывали у товарища текст выполненного задания и шли на собеседование, совершенно не подготовившись. (Обычно беседа заканчивалась на формуле длины вектора в трёхмерном пространстве: для её вычисления студенты предлагали найти корень кубический из суммы кубов его координат). В конце задачи прилагались пять вариантов ответа, один из которых был верным. (Все, естественно, указывали именно верный ответ).
На третий год преподавания эконометрики студентам по традиции была предложена задача о женских сапогах, но с элементом юмора: несколько значений объясняемой переменной были изменены (кроме начальных и конечных значений), причём таким образом, что теперь верным ответом стал другой из пяти вариантов. При беглом взгляде новый текст задания был очень похож на предыдущий, поэтому многие, не мудрствуя лукаво, выбирали прежний ответ, и затем «обосновывали» его. Таким образом, как всегда, перед преподавателем возникла задача обновления своих вариантов. Идеальным было бы, чтобы у каждого студента был вариант, не совпадающий с другими. Но таких вариантов в типичном случае понадобилось бы около ста, и проверка их преподавателем (даже по списку готовых ответов) превратилась бы в тяжкий труд. Так как многие из теперешних студентов выберут для себя нелёгкий труд преподавателя, можно заранее приоткрыть им кое-какие секреты составления «несписываемых» вариантов. Основная идея тут проста: заставить студента ломиться к решению задачи через центральный вход, а самому проникнуть в суть этой задачи через незаметный чёрный ход. Например, рассмотрим такую задачу по теории вероятностей: Задумано случайное целое число N от единицы до ста включительно. Вычислено значение N(N+1)(N+2)(N+3)+1. Какова вероятность того, что корень из этого числа тоже является целым числом? Ответ: вероятность равна единице, так как из всех таких чисел корень извлекается точно. Но доказать это нелегко. Теперь можно составить любое количество вариантов, меняя пределы выбора числа N.
Приступим к постановке основной задачи данной курсовой работы.
Постановка задачи
Ниже приведена задача на расчет регрессии с двумя объясняющими перменными и пятью вариантами ответов (один из которых верный). Составить варианты такой же задачи (и с тем же уровнем технической трудности) за счет малозаметного изменения исходных данных, причём таким образом, чтобы правильным ответом стал другой вариант (из того же списка ответов).
«ЗАДАЧА О ЖЕНСКИХ САПОГАХ»
(домаашняя работа по эконометрике)
Себестоимость женских сапог, изготавливаемых на фабрике «Рассвет» (в рублях) зависит от курса доллара и курса евро, так как в производстве используются материалы и из США, и из Франции. (В данном задании для упрощения считается, что курсы этих валют изменяются независимо. Иначе это задание относилось бы к исследованию временных рядов). Наблюдение за себестоимостью сапог при различных значениях курса доллара и курса евро дали следующие результаты:
