Пошаговое приближение распределения стоимости покупки к но­р­мальному закону распределения

Вид материала

Закон

Содержание Постановка задачи Ход решения Постановка задачи

Подобный материал:

• Лабораторная работа 1-08 экспериментальное изучение гауссовского закона распределения, 108.63kb.
• Дискретные случайные величины Ряд распределения, 29.73kb.
• Природа каналов распределения товаров. Их структура и управление, 20.88kb.
• Лабораторная работа №2 Тема: Формирование выборки случайных чисел, распределенных, 151.75kb.
• Функция распределения. Плотность распределения. Основные параметры непрерывных случайных, 7.05kb.
• Законом распределения, 13.27kb.
• Методы и каналы распределения товаров, 82.28kb.
• Лекция 10. Управление системой распределения >10. Управление системой распределения, 258.27kb.
• Задача оптимизации расположения распределительного центра на обслуживаемой территории, 872.4kb.
• Секция №1 Модераторы: В. Стрельченок, Е. Толстая, И. Ратанова, 183.54kb.

Постановка задачи

В небольшом городке испытывается новая модель электробритвы с повышенной комфортностью, но со сроком службы 1 год (рекламный слоган: «Целый год – без всяких хлопот»). Все лица, купившие такую бритву в теку­щем году, разбиты на возрастные группы: от 20-2,5 до 20+2,5 лет; от 25-2,5 до 25+2,5 лет, от 30-2,5 до 30+2,5 лет, . . . , от 80-2,5 до 80+2,5 лет. Условно считается, что в первой группе все потребители имеют возраст 20 лет, во вто­рой – 25, и так далее. Количества людей в каждой группе заданы таблицей:

Возраст	20	25	30	35	40	45	50	55	60	65	70	75	80
Колич.	11	93	163	178	176	132	100	67	40	24	12	3	1

Изучение гистограммы этих данных (котороая должна быть приведе­на в курсовой) показывает, что кривая распределения отходит от оси иксов, имеет одну точку максимума и затем снова плавно подходит к оси ик­сов. По классификации Пирсона это – кривая I типа. Начало таких кривых Пирсон предложил помещать в точку, где находится максимум, а ширину об­ла­сти определения выбирать некоторым стандартизованным образом (напо­мним, что от сжатия кривой распределения вдоль оси иксов площадь под кривой не изменяется и остается равной единице).

Ход решения

В нашем примере естественная область опреде­ления простирается от 20-2,5 года до 80+2,5 года. Стандартизованная же об­ласть простирается от (–3,017) условных возрастных единиц до 12,043 услов­ных возрастных единиц (формулы, по которым в теории Пирсона находятся границы области, здесь не рассматриваются). Таким образом, вместо прежних возрастных единиц («годы»), в которых ширина области определения равня­лась 65 лет, будут использованы условные единицы, в которых ширина обла­сти определения равна 3,017 + 12,043 = 15,06. Если по оси иксов по-прежнему откладываются годы, график придется сжать в несколько раз вдоль горизон­тали. и во столько же раз растянуть вдоль вертикали. Но если вместо годов выбрать условные единицы в качестве масштаба по оси иксов, то сжатия графика по горизонтали не будет, а будет просто смещение графика так, чтобы начало отсчета иксов совпало с точкой максимума кривой. Соответ­ственно, высота максимальной точки не изменится (в нашем случае оно примерно равно 178 (потребителей)). Кривая регрессии I типа подбирается по формуле, предложенной Пирсоном:


p(x) = K (1 + x/3,017)^a (1 – x/12,043)^b ,


где параметры a, b подбираются методом наименьших квадратов отклонения от экспериментальных данных (параметр K, для упрощения курсовой работы, не подбирается на компьютере, а просто принимается равным 178).

У нас заданы 13 экспериментальных данных в точках 20, 25, 30, …, 80 лет. Эти точки надо пересчитать с учетом перехода от годам к условным единицам и сдвига начала координат в точку максимума. Приближенное расположение точки максимума (если судить по таблице данных) : х = 33,5 лет. Пересчет делается путем вычитания из всех иксов 33,5 лет и умножения затем на поправочный множитель 15,06/67,5. Пояснение. Исходная ширина области определения кривой p(x) равна 65 лет, но ввиду медленного спадания её на правом краю области определения можно продлить кривую до значения 85 лет. Тогда длина области определения будет равна 67,5 лет.

Прежде чем делать подбор параметров a, b , надо убедиться, что все пересчитанные по формуле (х-33,5)*15,06/67,5 значения возраста лежат на естественной области определения приведенной вышн кривой Пирсона, то есть на отрезке (-3,017 ; 12,043). Это условие должно соблюдаться в течение всего процесса подбора параметров a, b. Исходные значения были взяты такие: a = 2, b = 5. При этом сумма квадратов отклонений равна 9120. После минимизации этой суммы путем вызова оптимизатора (пункты меню в Excel: Сервис, Поиск решения) получены значения a = 1,257 , b = 4,270 . Для этих значений сумма квадратов отклонений равна 292.

Приведем исходные и сглаженные значения кривой распределения для оптимизированных значений парметров a, b:


11 93 163 178 176 132 100 67 40 24 12 3 1

0,14 96,1 161 182 170 139 102 66,9 38,5 18,8 7,23 1,9 0,23


На рис.2 эти данные представлены в виде двух гистограмм.



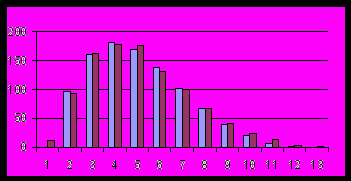
Рис. 2 Теоретическая (слева) и эмпирическая гистограммы


Имея явную теоретическую формулу для кривой распределения потребителей электробритв


p(x) = 178 (1 + x/3,017)^1,257 (1 – x/12,043)^4,270 ,


можно поставить на твердую почву решение многих макретинговых задач, например: как изменится объем покупок бритв в следующем году, если молодежь этого городка в возрасте от 17,5 и до 30 лет будет призвана на службу в армию. Задание 12 также посвящено этой тематике.


Задание 12.

Использование нелинейной кривой регрессии для расчета прибыли городской транспортной компании

Постановка задачи

Методами, изложенными в задании 11, была рассчитана кривая ин­тен­сивности использования городского транспорта жителями города К. Общее количество жителей равно 30000 человек., один билет на любой вид транспорта стоит 17 рублей за одну поездку (независимо от её длительности), один житель делает в среднем четыре поездки в день. Кривая имеет вид


p(x) = K (1 + x/3,017)^1,257 (1 – x/12,043)^4,270 ,

где К подбирается таким образом, чтобы суммарная площадь под кривой (на отрезке [-3,016; 12,042]) равнялась единице.


Пользователи транспорта разбиваются на возрастные группы (5, 10 лет), (10, 15 лет), …, (75, 80 лет). Стандартизованное значение х= –3,017 соответствует возрасту 5 лет, а значение х=12,043 – возрасту 80 лет.

Согласно распоряжению мэра города г-на Стручкова, со следующего года все жители города в возрасте 60 лет и выше будут пользоваться транс­портом бесплатно. Какой убыток (в пересчете на один месяц) потерпит от этого транспортная компания? Сколько процентов от дохода предыдущего года он составит? Вопрос на понимание ситуации: как Вы думаете, сможет ли компания покрыть убыток за счет сокращения количества единиц транспорта, обслуживающего население? Полностью ли она компенсирует убыток, если г-н Стручков даст компании дотацию в размере четырех поездок в день каж­до­му жителю в возрасте 60 лет и выше?