Пошаговое приближение распределения стоимости покупки к но­р­мальному закону распределения

Вид материала

Закон

Содержание Расчет кривой агрегированного спроса методом статистического моделирования. Рекомендуется для тем № 2, 4, 31 по списку, приведенному в конце основного текста. Расчет кривой спроса на конкретный товар на основе N данных, полученных из наблюдения цен на рынках г. Москвы. Постановка задачи Ход решения Замечания для преподавателей. Рекомендуется для тем № 24, 25, 29.

Подобный материал:

• Лабораторная работа 1-08 экспериментальное изучение гауссовского закона распределения, 108.63kb.
• Дискретные случайные величины Ряд распределения, 29.73kb.
• Природа каналов распределения товаров. Их структура и управление, 20.88kb.
• Лабораторная работа №2 Тема: Формирование выборки случайных чисел, распределенных, 151.75kb.
• Функция распределения. Плотность распределения. Основные параметры непрерывных случайных, 7.05kb.
• Законом распределения, 13.27kb.
• Методы и каналы распределения товаров, 82.28kb.
• Лекция 10. Управление системой распределения >10. Управление системой распределения, 258.27kb.
• Задача оптимизации расположения распределительного центра на обслуживаемой территории, 872.4kb.
• Секция №1 Модераторы: В. Стрельченок, Е. Толстая, И. Ратанова, 183.54kb.

Задание 5.

Расчет кривой агрегированного спроса методом статистического моделирования.


Замечания для преподавателей и постановка задачи. После предва­рительного расчета склады­ваются кривые индиви­ду­ального спроса на неде­лимый товар (телевизоры, холодильники, музыкальные центры и т.д.) в коли­честве N кривых. Индивидуальные кривые являются кусочно-постоянными и отли­чаются друг от друга ценовыми порогами, при которых изменяется коли­чество покупаемых изделий. Подробности моделированиия в среде Excel сообща­ются студентам на консуль­тациях по КМКР (ниже описан общий ход расче­тов). Эта тематика углуб­ляет представления студентов о спросе на неделимые товары и о механизме превращения кусочно– посто­янной кривой спроса в практически непрерывную.

Рекомендуется для тем № 2, 4, 31 по списку, приведенному в конце основного текста.

Ход решения

Допустим, что потребителя интересует неделимый товар «телевизор как функциональное устройство» (то есть он не обращает внимание на дизайн, габариты, удобство обслуживания и т.д.). Максимальная потребность в едини­цах такого товара ограничена числом 4 (один телевизор в спальне, один – на кухне, один в машине (шутка) и один на даче). Конкретно покупаемое коли­чество единиц товара может равняться 4, 3, 2, 1 или 0 (в зависимости от его цены). Типовая кусочно-постоянная кривая спроса для отдельного потреби­те­ля изображена ниже. Переключение количества покупаемых изделий проис­ходит при ценах, которые мы обозачим a, b, c, d. Для конкретности примем

a=900, b=1600, c=2000, d=5000 рублей.

Для этих значений параметров график спроса имеет вид:






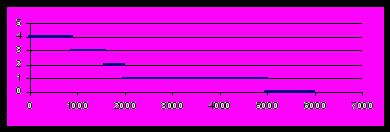
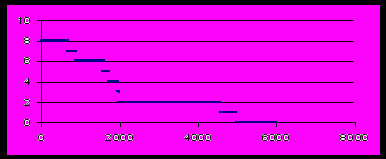
Затем необходимо построить 15-20 таких же кривых с другими пара­метрами a, b, c, d. Их можно получить с помощью датчика случайных чисел. После сложения всех этих кривых получится кривая агрегированного спроса для 15-20 потребителей. Она состоит из большого количества мелких ступе­ней, В случае 20 слагаемых максимальная высота этой кривой равна 20х4 = 80. Ниже приведен график суммы двух кривых, причем для второй a=700, b=1700, c=1980, d=4580.

Генерацию значений ступенчатой функции удобно делать с помощью формулы Excel следующего вида: Если(A1<700;4; Если(A1<1700;3; Если(A1< 1980;2; Если(A1<4580;1;0)))).

Суммирование 15-20 таких функций, записанных по столбцам, с ша­гом 50 рублей, для цен не свыше 8000 руб. за шт., позволяет построить ито-


говый график агрегированного спроса. Подробности генерации случайных значений параметров a, b, c, d сообщаются студенту на консультации (раз­ным студентам могут быть заданы разные законы распределения).

Задание 6.

Расчет кривой спроса на конкретный товар на основе N данных, полученных из наблюдения цен на рынках г. Москвы.

З
амечания для преподавателей. После сбора исходных данных о ценах на данный товар (данных надо собрать не менее 20, но и не более 50 (чтобы не увеличивать объем расчетов)) необходимо выбрать теоретическую формулу для подгонки. Можно считать, что исходные точки, хотя и имеют разброс, в целом лежат на кривой, выражаемой дробно-линейной функцией. Коэффициенты этой кривой подбираются методом наименьших квадратов (возможности Excel позволяют использоать даже нелинейный вариант этого метода). Литература по этому вопросу и метод исследования сообщаются на консультациях. Отметим только, что для получения реалистичной модели вертикальная асимптота дробно-линейной функции должна лежать в области x < 0, кривая при x > 0 должна быть убывающей, а горизонтальная асимптота должна лежать на высоте, которая меньше нуля (или равна нулю). Однако для построения кривой спроса необходимо знать не только цены на товар, но и (что гораздо проблематичнее) общий объем покупок, который согласились сделать потенциальные потребители товара при данной цене. Общий объем покупок можно оценить, фиксируя не только цену продажи, но и покупаемое количество товара. Так как все покупки зафиксировать невозможно (да и если бы это было сделано, еще пришлось бы выяснять, принадлежит ли покупатель к этому региону, или он приезжий), то необходимо сделать репрезентативную выборку и правильно обработать ее результаты. Поэтому в данном задании считается, что точки на кривой спроса уже получены, но их надо сгладить. Со статистической точки зрения представляет интерес изменение коэффициентов дробно-линейной функции при последовательном наращивании допол­нитель­ных точек на кривой спроса. Генерацию дополнительных точек, содержащих случайные добавки, можно осуществить на компьютере, взяв за основу зара­нее известную дробно-линейную функцию, отвеча­ющую упомянутым выше условиям), и прибавляя к ней независимые случайные числа, распределенные по нормальному закону. Изобразив графически серию кривых, получаемых при добавлении всё новых и новых точек, можно увидеть характер стрем­ления этих кривых к предельной кривой.

Рекомендуется для тем № 6, 27, 29.

Постановка задачи

На рынках города Москвы в определенный день была зафиксирована усредненная цена 1 л молока 3,5%-ой жирности и определено оценочное ко­ли­чество литров закупленного продукта. Затем то же самое было проделано в несколько других дней, что позволило получить несколько точек на кривой спроса, искаженных влиянием неучтенных случайных факторов. Произвести расчет коэффициентов кривой спроса в виде дробно-линейной функции D = (ap + b) / (p + c) , где D – спрос, p – цена товара. Сначала сделать расчет параметров a, b, c по семи точкам, затем постепенно довести количество точек до 12. Изобразить получен­ные 6 кривых на одном чертеже и сделать выводы о том, стабилизируется ли кривая.

Ход решения

Методика будет изложена для случая пяти точек (p1, D1), (p2, D2), (p3, D3), (p4, D4), (p5, D5).

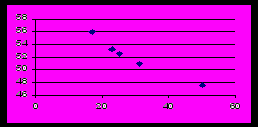
Из экспериментального значения спроса D1 вычитается его теорети­ческое значение (a*p1 + b) / (p1 + c) , и полученное отклонение возводится в квадрат. Сумма квадратов отклонений минимизируется с помощью встроен­ного оптимизатора Excel. Получаются подогнанные значения параметров a, b, c. Для отладки методики рассмотрим дробно –линейную функцию D = (40p + 1000) / (p + 13), выберем пять произвольных значений p и рассчитаем соответ­ствующие значения D. Затем приплюсуем к ним случайные добавки, незначи­тельно изменяющие D.

Числовая иллюстрация. Выбираем p = 17, 23, 25, 31, 50 и вычисляем точные значения D = 56,00; 53,33; 52,63; 50,91; 47,62. Графическое изображение этих точек дано ниже.

Вносим случайные возмущения в значения D и получаем новые пять значений:

56,0 53,3 52,6 50,9 47,6 .







Вызываем пункты меню Excel «Сервис», «Поиск решения», взяв такое исходное приближение для a, b, c: 41; 998; 12. Целе­вая функция вычис­ляется как сумма квадратов откло­нений эксперимен­таль­ных значений спроса от теоретических. Для исходных значений подбира­е­мых пара­метров она равна 20,88. После минимизации она равна 0,000743. Опти­ми­зированные зна­чения a, b, c рав­ны 39,98; 998; 12,96 . (Это близко к значениям 40, 1000, 13 , взятых для тестирования).


Задание 7.

Статистическое исследование феномена «отложенной реали­зации» с привлечением показа­теля NPV и учёта случайных изме­нений процентной ставки.

Замечания для преподавателей. Основная задача: приобретается пар­тия бутылок вина, которое от длительного хранения улучшает свои потреби­тельские качества. Сколько процентов товара надо продавать в том же году, сколько – через три года, сколько – через 6 лет? Для имитации изменения про­центной ставки используются датчики случайных чисел Excel.

Рекомендуется для тем № 24, 25, 29.