Дискретные случайные величины Ряд распределения

Вид материала

Документы

Подобный материал:

• Случайные величины и функции распределения, 49.56kb.
• Задачи линейного программирования. 17. Дискретные случайные величины, 24.38kb.
• Конспект лекции для автора курсового проекта как для преподавателя Дискретные случайные, 103.41kb.
• Программа вступительных испытаний по предмету прикладная математика и информатика для, 16.87kb.
• Основные виды случайных величин, 28.43kb.
• Программа государственного экзамена по направлению (магистерская подготовка) 230100., 37.35kb.
• Линейная регрессия и метод наименьших квадратов, 177.63kb.
• Числовые характеристики случайных величин, 50.29kb.
• Лекция Случайные величины и их распределения, 84.03kb.
• Вопросы к экзаменам 3-й курс вмк вопросы для темы, 70.75kb.

Дискретные случайные величины


Ряд распределения. Дискретная случайная величина 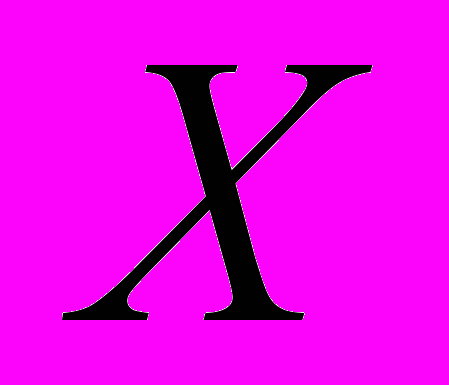определяется своим рядом распределения, т.е. таблицей вида

				…
				…

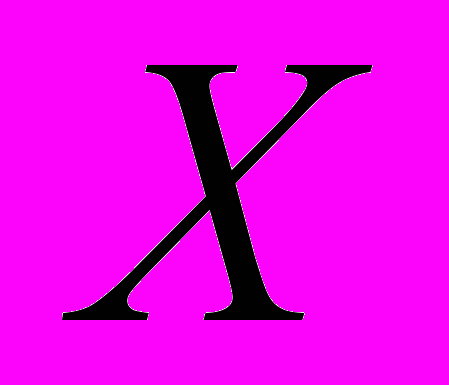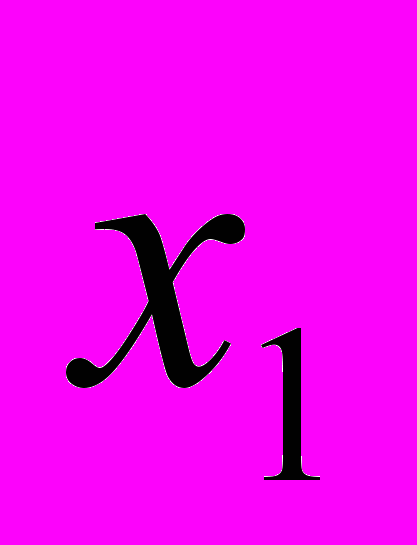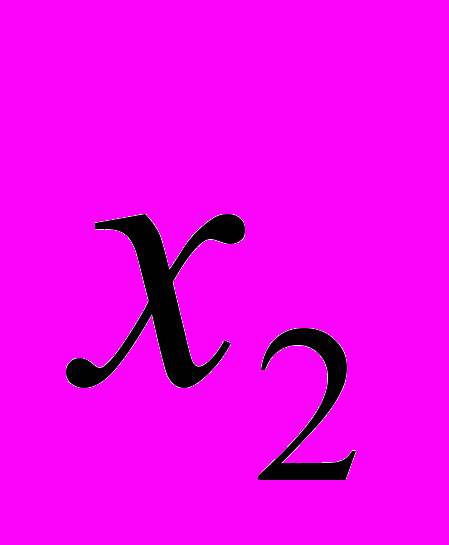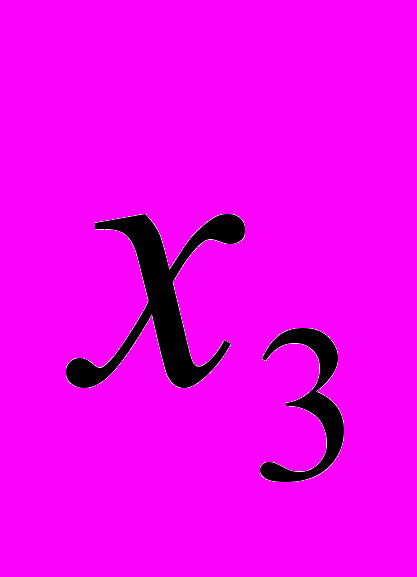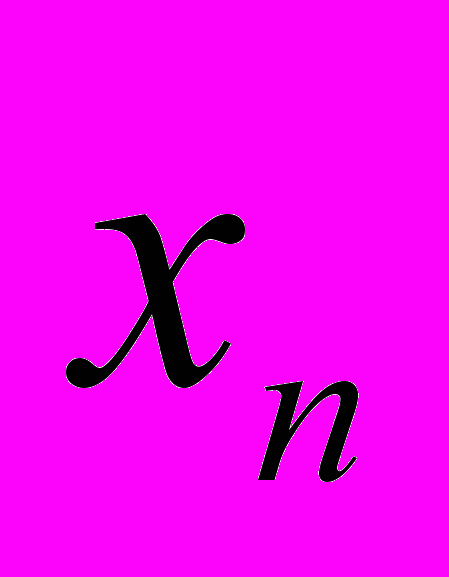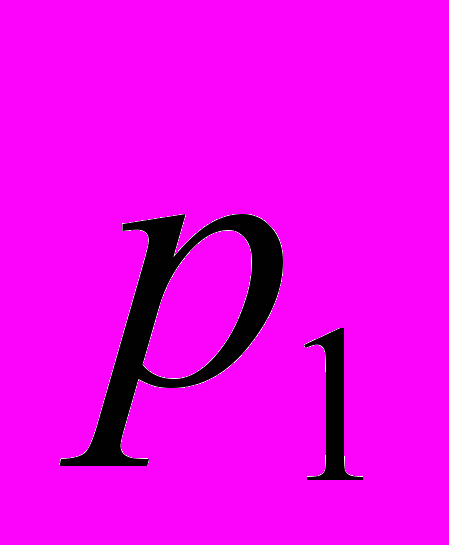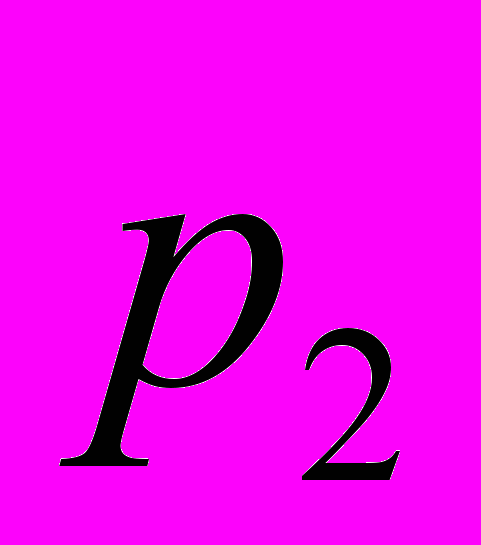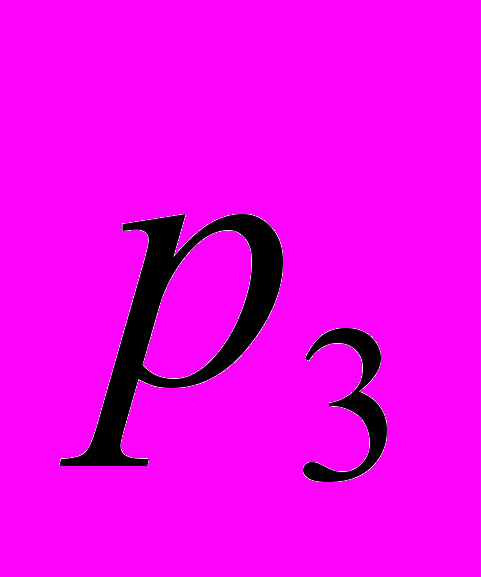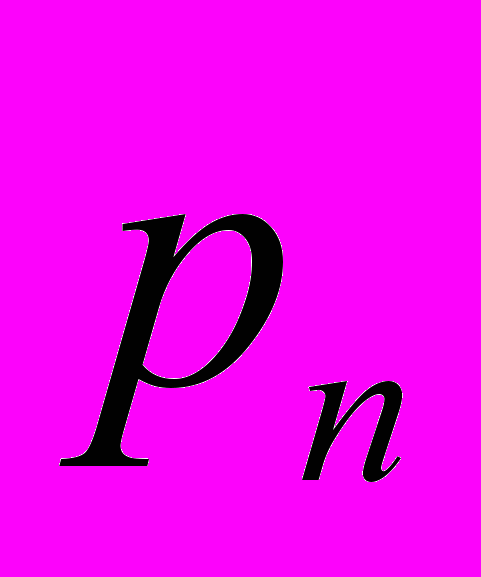В ней в первой строке стоят в порядке возрастания значения 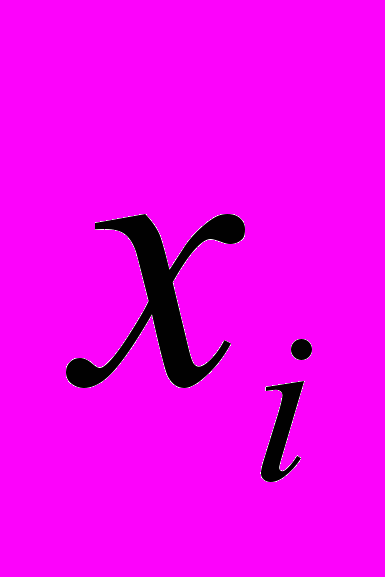, которые может принимать случайная величина, а во второй – вероятности 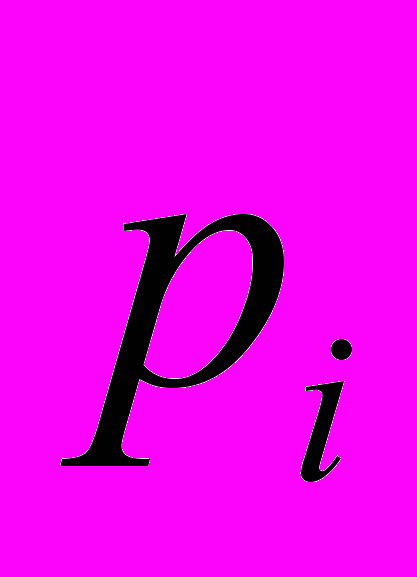, с которыми эти самые значения принимаются. Все вероятности неотрицательны и их сумма равна 1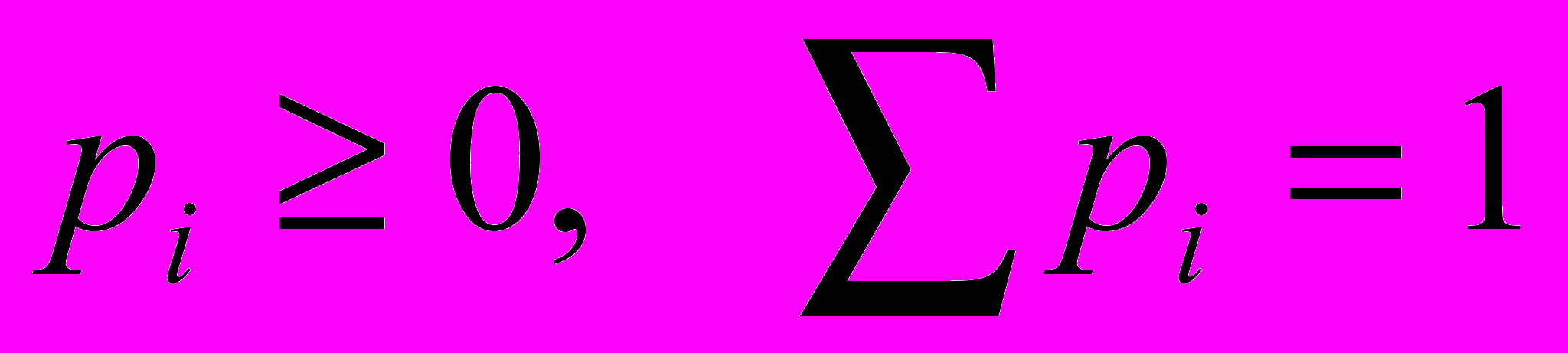


.


Так если случайная величина 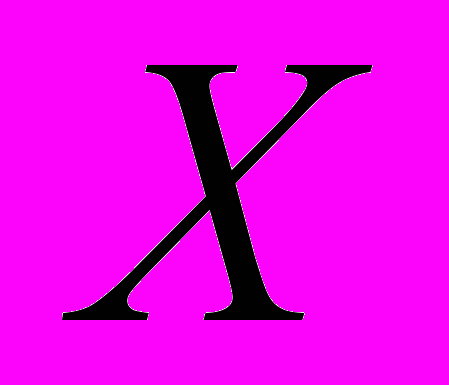– это количества выпавших очков на грани брошенного игрального кубика, то ее ряд распределения имеет вид

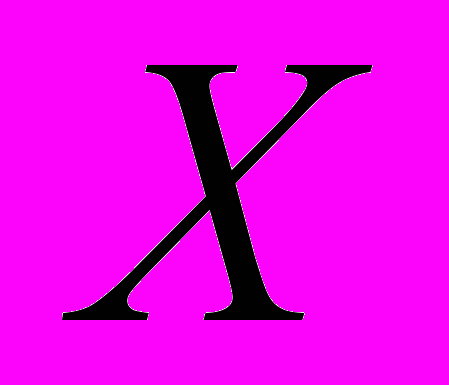	1	2	3	4	5	6
	1/6	1/6	1/6	1/6	1/6	1/6

Если случайная величина 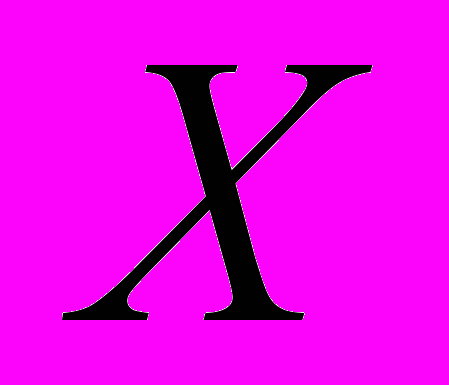– это сумма очков на гранях двух одновременно брошенных игральных кубиков, ее ряд распределения имеет вид

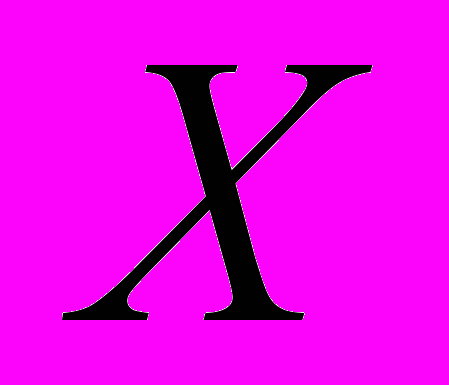	2	3	4	5	6	7	8	9	10	11	12
	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

Упражнение. Составить ряды распределения для случайных величин:

• количество выпадения герба при однократном бросании монеты
  
• количество выпадения герба при двукратном бросании монеты
  
• количество выпадения герба при трехкратном бросании монеты
  
• количество выпадения герба при четырехкратном бросании монеты
  
• сумма очков на случайно выбранной костяшке домино
  

Многоугольник распределения, гистограмма распределения. Для того чтобы можно было геометрически изобразить закон распределения, на оси абсцисс будем откладывать значения случайной величины 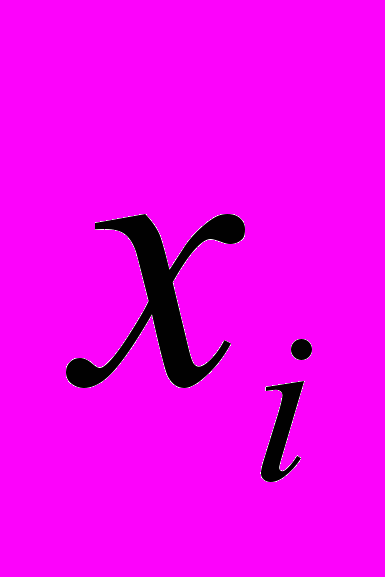, а вдоль оси ординат – соответствующие значения вероятностей. Ломаная, проходящая через точки 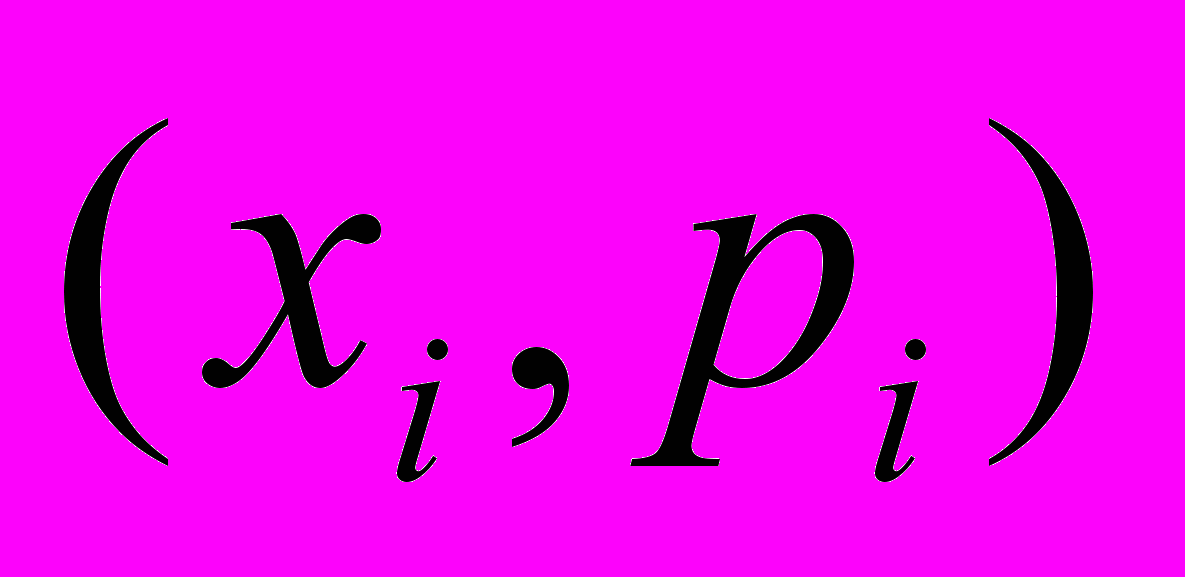, называется многоугольником распределения, а соответствующая гистограмма – гистограммой распределения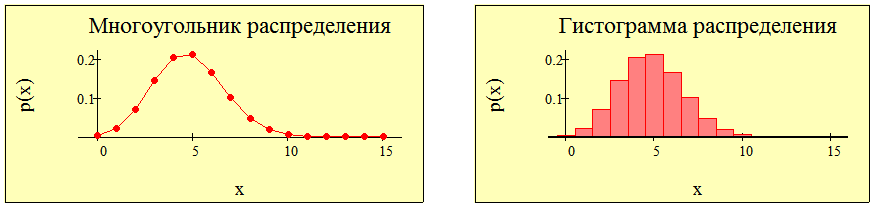





Упражнение. Построить многоугольники распределения и гистограммы для случайных величин из предыдущего упражнения.