Конспект лекции для автора курсового проекта как для преподавателя Дискретные случайные величины и их числовые характеристики

Вид материала

Конспект

Содержание Функцией распределения Свойства функции распределения Средним квадратическим отклонением Биномиальный закон распределения X, имеющей биномиальный закон распределения с параметрами n Закон распределения Пуассона

Подобный материал:

• Случайные величины и функции распределения, 49.56kb.
• Линейная регрессия и метод наименьших квадратов, 177.63kb.
• Задачи линейного программирования. 17. Дискретные случайные величины, 24.38kb.
• Дискретные случайные величины Ряд распределения, 29.73kb.
• Числовые характеристики случайных величин, 50.29kb.
• Методические указания к выполнению курсового проекта Красноярск 2002, 2057.27kb.
• Программа государственного экзамена по направлению (магистерская подготовка) 230100., 37.35kb.
• Методические указания по выполнению курсового проекта для специальности 190631 «Техническое, 957.7kb.
• Методические материалы для выполнения курсового проекта по дисциплине «Проектирование, 635.61kb.
• Методические указания по выполнению курсового проекта Тема курсового проекта, 265.09kb.

Конспект лекции для автора курсового проекта как для преподавателя


Дискретные случайные величины и их числовые характеристики


Дискретная случайная величина (ДСВ) может принимать конечное или бесконечное счетное число значений.

Пример ДСВ – число точек на грани игрального кубика, выпадающее при его подбрасывании.

!Задание привести пример ДСВ из окружающей жизни

Законом распределения ДСВ называется соотношение между ее возможными значениями и их вероятностями (т. е. вероятностями, с которыми случайная величина принимает эти возможные значения).

Закон распределения может быть задан формулой (формулы Бернулли, Пуассона и др.), таблицей или графиком, а также функцией распределения.

Функцией распределения случайной величины называется функция  

,

определяющая вероятность того, что случайная величина примет значение, меньшее .


Свойства функции распределения:

а) функция распределения принимает значения только из отрезка [0,1]:

0 ≤ F(x) ≤ 1;

б) F(x) – неубывающая функция, т.е. если x₂ > x₁, то F(x₂) > F(x₁) ;

в) F(- ∞ ) = 0; F(+ ∞) = 1;

г) вероятность того, что случайная величина примет значение из

интервала (причем ), равна:

 

;

 

д) F(x) непрерывна слева, т. е. F(x) = F(x – 0)


Закон распределения дискретной случайной величины может быть представлен в виде многоугольника распределения – фигуры, состоящей из точек , соединенных отрезками (рис. 1.3).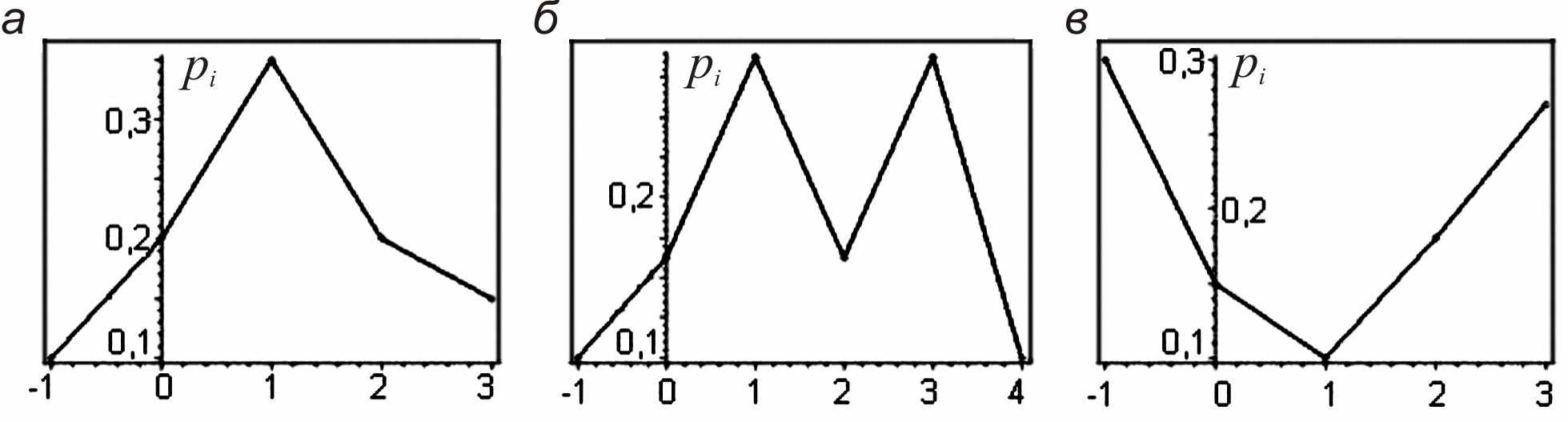

 



 

Рис. 1.3. Многоугольники унимодального (а), полимодального (б) и антимодального (в) распределений

 

Математическим ожиданием ДСВ называется среднее значение данной случайной величины

 

,

 

т. е. математическое ожидание – это сумма произведений значений случайной величины на соответствующие вероятности .


Свойства математического ожидания.

а) , где ;

б) ;

в) ;

г) если случайные величины и независимы, то .


Мода распределения – это значение СВ, имеющее наиболее вероятное значение. Если мода единственна, то распределение называется унимодальным (рис. 1.3, а), в противном случае – полимодальным (рис. 1.3, б) Если в середине диапазона изменения аргумента наблюдается минимум на графике многоугольника вероятностей, тогда распределение называется антимодальным (рис. 1.3, в).

 

Медиана – это значение случайной величины, которое делит таблицу распределения на две части таким образом, что вероятность попадания в одну из них равна 0,5

 

.

 

Медиана обычно не определяется для дискретной случайной величины.

Величина , определяемая равенством , называется квантилью порядка . Соответственно квантиль порядка 0,5 является медианой.


Дисперсией ДСВ называется математическое ожидание квадрата отклонения СВ от ее математического ожидания

 

,

.

 

Дисперсия служит для характеристики рассеяния СВ относительно ее математического ожидания


Свойства дисперсии:

а) , где ;

б) ;

в),

где – ковариация двух случайных величин и ;

г) если и некоррелированы, то , тогда .


Средним квадратическим отклонением называется величина, которая имеет ту же размерность, что и СВ :

 

.

 

Пример Дискретная случайная величина задана законом распределения:

	-1	0	1	2
	0,1	0,2	0,1	0,6

 

Найти числовые характеристики СВ: , моду.

Решение. Построим многоугольник распределения данной случайной величины.

 

Математическое ожидание:

 Дисперсия:



СКО:

Мода равна 2.

 

Основные законы распределения дискретных случайных величин


1. Закон распределения Бернулли. Случайная величина , распределенная по закону Бернулли, принимает значения: 1 – «успех» или 0 – «неудача» с вероятностями и соответственно

	0	1

 

Математическое ожидание: СВ X: .

Дисперсия: .


2. Биномиальный закон распределения. Случайная величина , распределенная по биномиальному закону, принимает значения:

0, 1, 2, …, n с вероятностями, определяемыми по формулам Бернулли:



 

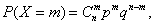
	0	1	2	,,,		,,,

 

Математическое ожидание: .

Дисперсия: .

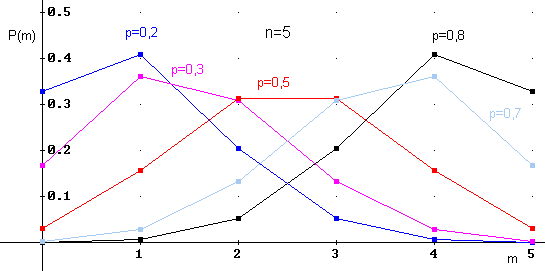
На рисунке приведены многоугольники (полигоны) распределения случайной величины X, имеющей биномиальный закон распределения с параметрами n=5 и p (для p=0,2; 0,3; 0,5; 0,7; 0,8).




Пример . В рекламных целях торговая фирма вкладывает в каждую пятую единицу товара денежный приз размером 100 тенге. Найти закон распределения числа сотен тенге, полученных при четырёх сделанных покупках.


Решение Вероятность того, что в случайно сделанной покупке окажется денежный приз, равна p=1/5=0,2. Случайная величина X - число покупок, в которые вложен денежный приз, имеет биномиальный закон распределения с параметрами n=4 и p=0,2. Ряд распределения X имеет вид:

xi	0	1	2	3	4
pi	0,4096	0,4096	0,1536	0,0256	0,0016

значения p_i=P(X=m), (m=0, 1, 2, 3, 4) вычислены по формуле

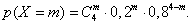
!Задание построить многогранник распределения


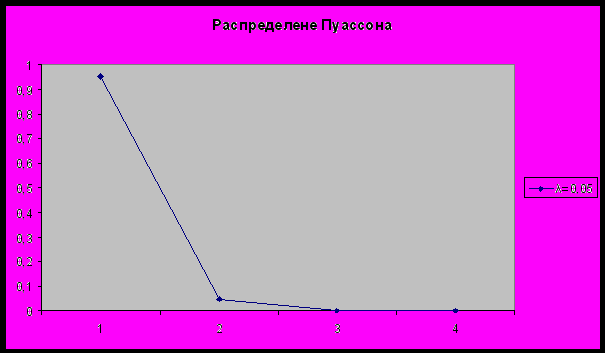
3. Закон распределения Пуассона. Случайная величина , распределенная по закону Пуассона, принимает бесконечное счетное число значений: 0, 1, 2, …, k, …, с соответствующими вероятностями, определяемыми по формуле Пуассона

,

где – параметр распределения Пуассона.

На рисунке приведены многоугольники (полигоны) распределения случайной величины X, имеющей закон распределения Пуассона с параметром 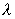 (для 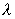=0,5; 1; 2; 3,5; 5).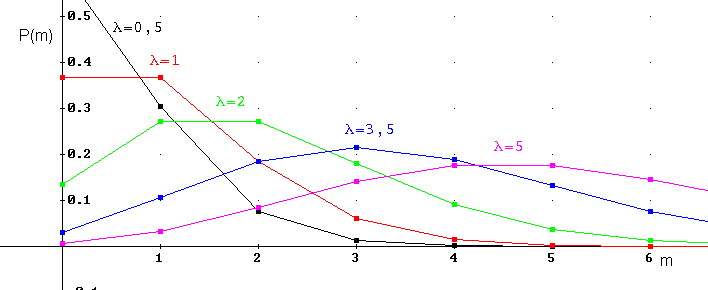




При и биномиальный закон распределения приближается к закону распределения Пуассона, где .

Математическое ожидание .

Дисперсия .


Пример В супе объёмом V плавает N перчинок. С какой вероятностью в ложку объёмом V₀ попадёт ровно n перчинок?

Решение

Если количество перчинок N велико, а отношение 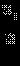мало, то задача описывается распределением Пуассона.

В среднем, в ложке должны оказаться 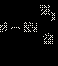перчинок. Вероятность того, что в ложке окажется ровно n перчинок, равна 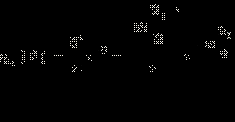В частности, при V = 10 л, 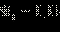л, N = 50 получаем 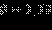(то есть одна перчинка, в среднем, попадается на 20 ложек), а вероятность:

• того, что в ложке окажется ноль перчинок, p₀ ≈ 0,95123,
  
• того, что в ложке окажется одна перчинка, p₁ ≈ 0,04756,
  
• того, что в ложке окажется две перчинки, p₂ ≈ 0,00119,
  
• того, что в ложке окажется три перчинки, p₃ ≈ 0,00002.
  

Как видим, p_n очень быстро уменьшается с ростом n.




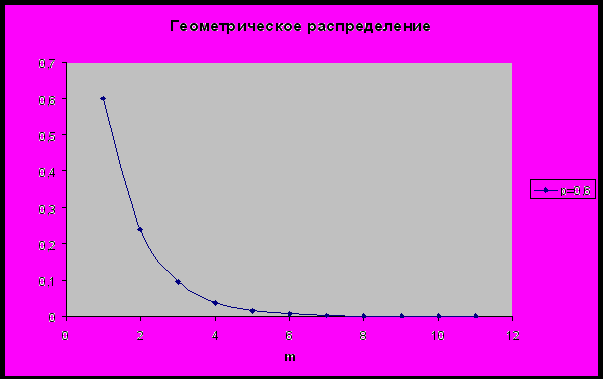
4) Геометрическое распределение. Дискретная случайная величина X имеет геометрическое распределение, если она принимает значения 1, 2, ..., m, ... (бесконечное, но счётное множество значений) с вероятностями





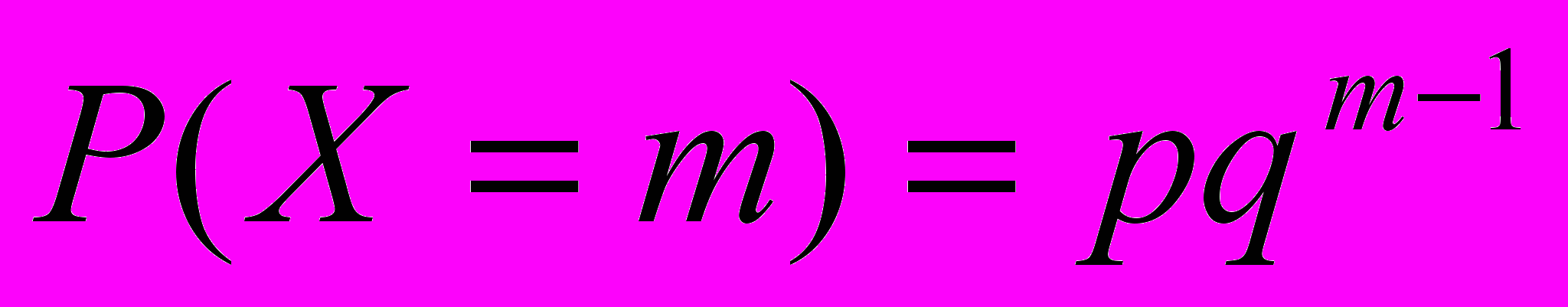
где 0 < p < 1, q=1 - p, m =1, 2, ...


Пример геометрического распределения представлен на рисунке




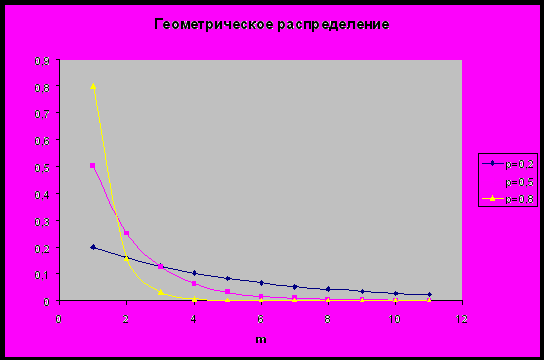
Ряд геометрического распределения имеет вид:

xi	1	2	3	...	m	...
pi	p	pq	pq2	...	pqm-1	...

Очевидно, что вероятности p_i образуют геометрическую прогрессию с первым членом  p и знаменателем q (отсюда и название "геометрическое распределение").


Определение геометрического распределения корректно, так как сумма ряда



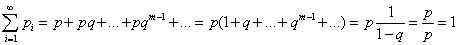
(так как 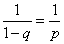есть сумма геометрического ряда 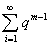при ).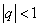

Случайная величина X=m, имеющая геометрическое распределение, представляет собой число m испытаний, проведённых по схеме Бернулли, с вероятностью p наступления события в каждом испытании до первого положительного исхода.

Математическое ожидание СВ X, имеющей геометрическое распределение с параметром p,

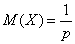
Дисперсия 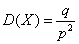, где q= 1-p.


Пример. Вероятность поражения цели равна 0,6. Производится стрельба по мишени до первого попадания (число патронов не ограничено). Требуется составить ряд распределения числа сделанных выстрелов, найти математическое ожидание и дисперсию этой случайной величины. Определить вероятность того, что для поражения цели потребуется не более трёх патронов.

Решение.  Случайная величина X - число сделанных выстрелов - имеет геометрическое распределение с параметром p=0,6. Ряд распределения X имеет вид:

xi	1	2	3	...	m	...
pi	0,6	0,24	0,096	...	0,6·0,4m	...

По формулам

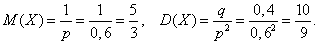
Вероятность того, что для поражения цели потребуется не более трёх патронов равна

P(X≤3)=P(X=1)+P(X=2)+P(X=3)=0,6+0,24+0,096=0,936.

 

Ответы на вопросы:

1. Какие элементы лекции направлены на обеспечение лучшего усвоения материала аудиторией на уровнях:

• понимания; - основные определений.
  
• опознания; - формулы, графики, таблицы.
  
• воспроизведения; - примеры, графики.
  
• применения; - примеры.
  
• творческой деятельности. – решение примеров.
  

2. Чем конкретно использование электронных ресурсов повышает эффективность лекции?

Ответ: Электронные ресурсы повышают интерес у студентов, а также помогают преподавателю изложить материал как можно понятней с различными примерами и т.д.

3. Почему презентация способствует лучшему пониманию данного материала на лекции данной аудиторией?

Ответ: Т.к в презентации в сокращенной, и в понятной форме описана суть лекции, презентация более визуально, что задействует не только слухавую но и другие виды памяти

4. Почему используемая компьютерная программа способствует лучшему пониманию данного материала на лекции данной аудиторией?

Ответ: Потому что программный модуль является тестовым вариантом лекции, что способствует оценки знаний и и остаточного контроля знаний.

5. Что даст аудитории и самому лектору использование на лекции фрагментов теста?

Ответ: Фрагменты теста, дадут возможность лектору оценить степень внимания студентов и уяснить кто из них слушает лекцию внимательно, а кто отвлеченно.