Лекция Случайные величины и их распределения
| Вид материала | Лекция |
Содержание6.2. Дискретные распределения Примеры дискретных распределений Распределение Бернулли. Геометрическое распределение. Распределение Пуассона. |
- Случайные величины и функции распределения, 49.56kb.
- Дискретные случайные величины Ряд распределения, 29.73kb.
- Программа вступительных испытаний по предмету прикладная математика и информатика для, 16.87kb.
- Основные виды случайных величин, 28.43kb.
- Программа государственного экзамена по направлению (магистерская подготовка) 230100., 37.35kb.
- Линейная регрессия и метод наименьших квадратов, 177.63kb.
- Вопросы к экзаменам 3-й курс вмк вопросы для темы, 70.75kb.
- Московский институт радиотехники, электроники и автоматики, 121.14kb.
- Задачи по теории вероятностей и математической статистике, 57.05kb.
- Лабораторная работа 1-08 экспериментальное изучение гауссовского закона распределения, 108.63kb.
Лекция 6. Случайные величины и их распределения
- Случайные величины
- Дискретные распределения
- Примеры дискретных распределений
- Примеры дискретных распределений

6.1. Случайные величины
Мы уже видели, что для очень многих экспериментов нет никаких различий в подсчете вероятностей событий, тогда как элементарные исходы в этих экспериментах очень различаются. Но нас и должны интересовать именно вероятности событий, а не структура пространства элементарных исходов. Поэтому пора во всех таких «похожих» экспериментах вместо самых разных элементарных исходов использовать, например, числа. То есть ввести соответствие (иначе говоря, отображение) между элементарными исходами и вещественными числами (с ними удобно работать).
Пусть имеется случайный эксперимент и задано вероятностное пространство
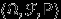 .
. Определение 24.
Функция
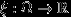 называется случайной величиной, если для любого
называется случайной величиной, если для любого 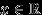 множество элементарных исходов
множество элементарных исходов 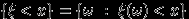
является событием, то есть принадлежит
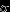 -алгебре событий
-алгебре событий 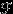 .
. Это нужно ровно затем, чтобы вероятность такого множества была определена! Напомню: вероятность есть неотрицательная, счетно-аддитивная функция, определенная только на множествах из сигма-алгебры
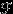 .
.Замечание 9.
Читатель, не желающий забивать себе голову абстракциями, связанными с
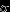 -алгебрами событий и с измеримостью, может смело считать, что любое множество элементарных исходов есть событие, и, следовательно, случайная величина есть произвольная функция из
-алгебрами событий и с измеримостью, может смело считать, что любое множество элементарных исходов есть событие, и, следовательно, случайная величина есть произвольная функция из 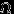 в
в 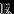 . Никаких неприятностей на практике это обычно не влечет, так что все дальнейшее в этом параграфе можно пропустить. Полезно, тем не менее, помнить: каждая такая «уступка» себе существенно снижает ваши адаптивные способности к жизни. ;-))
. Никаких неприятностей на практике это обычно не влечет, так что все дальнейшее в этом параграфе можно пропустить. Полезно, тем не менее, помнить: каждая такая «уступка» себе существенно снижает ваши адаптивные способности к жизни. ;-)) Определение 25.
Будем говорить, что функция
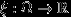 является
является 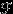 -измеримой, если
-измеримой, если 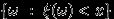
принадлежит
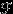 для любого
для любого 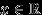 .
. Итак, случайная величина есть
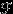 -измеримая функция, ставящая в соответствие каждому элементарному исходу
-измеримая функция, ставящая в соответствие каждому элементарному исходу 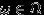 число
число 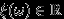 .
. Пример 23.
Подбрасываем 1 раз кубик. Пусть
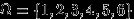 , и две функции из
, и две функции из 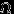 в
в 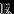 заданы так:
заданы так: 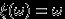 ,
, 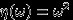 .
. - Если
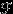 есть множество всех подмножеств
есть множество всех подмножеств 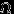 , то
, то  и
и 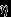 являются случайными величинами, поскольку любое множество элементарных исходов принадлежит
являются случайными величинами, поскольку любое множество элементарных исходов принадлежит 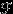 , в том числе и
, в том числе и 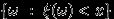 или
или 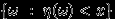 . Можно записать соответствие между значениями случайных величин
. Можно записать соответствие между значениями случайных величин  и
и  и вероятностями принимать эти значения в виде «таблицы распределения вероятностей» или, коротко, «таблицы распределения»:
и вероятностями принимать эти значения в виде «таблицы распределения вероятностей» или, коротко, «таблицы распределения»:
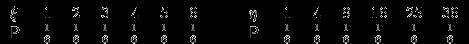
Здесь
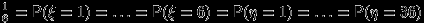 .
. - Пусть
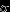 -алгебра событий
-алгебра событий 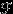 состоит всего из четырех множеств:
состоит всего из четырех множеств:
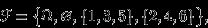
то есть событием является, кроме достоверного и невозможного событий, выпадение четного (соответственно, нечетного) числа очков. Убедимся, что при такой «бедной»
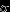 -алгебре ни
-алгебре ни  , ни
, ни 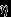 не являются случайными величинами, так как эти функции не
не являются случайными величинами, так как эти функции не 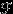 -измеримы. Возьмем (например)
-измеримы. Возьмем (например) 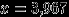 . Видим, что
. Видим, что 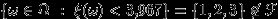 и
и 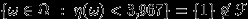 .
. - Упражнение. Описать класс всех функций, измеримых относительно
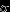 -алгебры
-алгебры 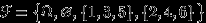 .
.
Пусть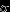 -алгебра событий
-алгебра событий 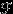 есть тривиальная
есть тривиальная 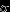 -алгебра :
-алгебра : 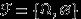 .
.
Упражнение.
Доказать, что
 и
и 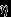 не являются случайными величинами, так как эти функции не
не являются случайными величинами, так как эти функции не 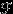 -измеримы.
-измеримы. Доказать, что измеримы относительно тривиальной
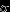 -алгебры только функции вида
-алгебры только функции вида 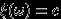 (постоянные).
(постоянные). Теперь попробуем понять, зачем нужна
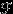 -измеримость и почему требуется, чтобы
-измеримость и почему требуется, чтобы 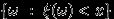 являлось событием.
являлось событием. Если задана случайная величина
 , нам может потребоваться вычислить вероятности типа
, нам может потребоваться вычислить вероятности типа 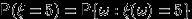 ,
, 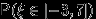 ,
, 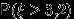 ,
, 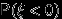
(и вообще самые разные вероятности попадания в различные множества на прямой). Это возможно только если множества, стоящие под знаком вероятности, являются событиями (еще раз напомню, что вероятность есть функция из
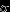 -алгебры событий в [0,1]).
-алгебры событий в [0,1]). Но если потребовать, чтобы
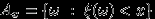 было событием при любом
было событием при любом 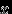 , то мы из свойств
, то мы из свойств 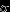 -алгебры сразу получим, что
-алгебры сразу получим, что 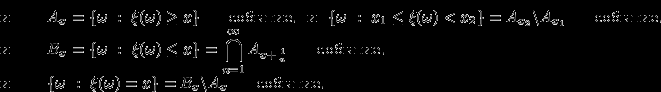 | (11) |
и т.д., и т.п. (операции пересечения, объединения, дополнения событий не выводят из класса событий).
Можно потребовать в определении 24 чего-нибудь другого. Например, чтобы событием было попадание в любой интервал:
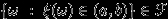 для любых
для любых 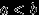 . Или чтобы
. Или чтобы 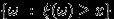 было событием для любого
было событием для любого 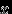 . Любое такое определение эквивалентно исходному.
. Любое такое определение эквивалентно исходному. Замечание 10.
Те, кто не поленился прочесть про борелевскую
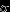 -алгебру в разделе 3.3, могут сформулировать все наши потребности так: мы хотим, чтобы попадание
-алгебру в разделе 3.3, могут сформулировать все наши потребности так: мы хотим, чтобы попадание  в любое борелевское множество являлось событием. Мы могли это потребовать в определении, но ограничились эквивалентным условием, чтобы попадание в любой открытый интервал
в любое борелевское множество являлось событием. Мы могли это потребовать в определении, но ограничились эквивалентным условием, чтобы попадание в любой открытый интервал 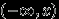 было событием. Эти условия эквивалентны, поскольку борелевская
было событием. Эти условия эквивалентны, поскольку борелевская  -алгебра порождается интервалами, что мы еще раз показали в формулах (11).
-алгебра порождается интервалами, что мы еще раз показали в формулах (11). Опишем различные типы распределений случайных величин. Под распределением случайной величины мы будем понимать соответствие
«значение случайной величины
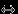 вероятность принимать это значение»,
вероятность принимать это значение», либо (чаще)
«множество на прямой
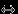 вероятность случайной величине попасть в это множество».
вероятность случайной величине попасть в это множество». 
6.2. Дискретные распределения
Определение 26.
Говорят, что случайная величина
 имеет дискретное распределение, если существует конечный или счетный набор чисел
имеет дискретное распределение, если существует конечный или счетный набор чисел 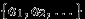 такой, что:
такой, что: а)
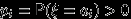 для всех
для всех 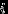 ;
; б)
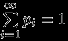 .
. То есть случайная величина
 имеет дискретное распределение, если она принимает не более чем счетное число значений.
имеет дискретное распределение, если она принимает не более чем счетное число значений. Определение 27.
Если случайная величина
 имеет дискретное распределение, назовем таблицей распределения соответствие
имеет дискретное распределение, назовем таблицей распределения соответствие 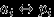 , которое чаще всего рисуют так:
, которое чаще всего рисуют так:  | 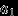 | 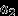 | 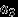 | ... |
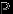 | 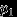 | 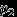 | 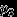 | ... |
Примеры дискретных распределений
Вырожденное распределение.
Говорят, что случайная величина
 имеет вырожденное распределение с параметром
имеет вырожденное распределение с параметром 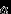 , и пишут
, и пишут 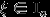 , если
, если  принимает единственное значение
принимает единственное значение 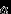 с вероятностью 1, то есть
с вероятностью 1, то есть 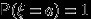 . Таблица распределения
. Таблица распределения  имеет вид
имеет вид  | 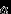 |
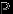 | 1 |
Распределение Бернулли.
Говорят, что случайная величина
 имеет распределение Бернулли с параметром
имеет распределение Бернулли с параметром 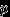 , и пишут
, и пишут 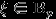 , если
, если  принимает значения 1 и 0 с вероятностями
принимает значения 1 и 0 с вероятностями 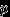 и
и 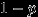 , соответственно. Случайная величина
, соответственно. Случайная величина  с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха
с таким распределением равна числу успехов в одном испытании схемы Бернулли с вероятностью успеха 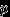 (0 успехов или 1 успех). Таблица распределения
(0 успехов или 1 успех). Таблица распределения  имеет вид
имеет вид  | 0 | 1 |
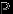 | 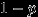 | 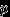 |
Биномиальное распределение.
Говорят, что случайная величина
 имеет биномиальное распределение с параметрами
имеет биномиальное распределение с параметрами 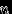 и
и 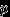 , где
, где 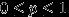 , и пишут
, и пишут 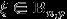 , если
, если  принимает значения
принимает значения 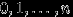 с вероятностями
с вероятностями 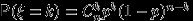 . Случайная величина
. Случайная величина  с таким распределением имеет смысл числа успехов в
с таким распределением имеет смысл числа успехов в  испытаниях схемы Бернулли с вероятностью успеха
испытаниях схемы Бернулли с вероятностью успеха 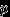 .
. Таблица распределения
 имеет вид
имеет вид 
Геометрическое распределение.
Говорят, что случайная величина
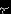 имеет геометрическое распределение с параметром
имеет геометрическое распределение с параметром 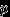 , где
, где 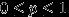 , и пишут
, и пишут 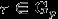 , если
, если 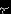 принимает значения
принимает значения 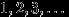 с вероятностями
с вероятностями 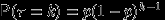 . Случайная величина
. Случайная величина 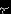 с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха
с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха 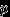 .
. Таблица распределения
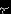 имеет вид
имеет вид 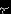 | 1 | 2 | ... | 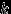 | ... |
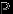 | 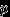 | 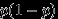 | ... | 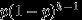 | ... |
Распределение Пуассона.
Говорят, что случайная величина
 имеет распределение Пуассона с параметром
имеет распределение Пуассона с параметром 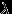 , где
, где 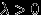 , и пишут
, и пишут 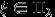 , если
, если  принимает значения
принимает значения 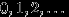 с вероятностями
с вероятностями 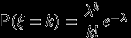 .
. Таблица распределения
 имеет вид
имеет вид  | 0 | 1 | ... | 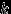 | ... |
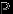 | 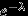 | 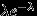 | ... | 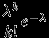 | ... |
Гипергеометрическое распределение.
Говорят, что случайная величина
 имеет гипергеометрическое распределение с параметрами
имеет гипергеометрическое распределение с параметрами 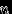 ,
, 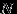 и
и 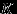 , где
, где 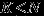 ,
, 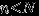 , если
, если  принимает целые значения от
принимает целые значения от 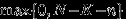 до
до 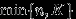 с вероятностями
с вероятностями 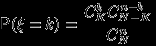 . Случайная величина
. Случайная величина  с таким распределением имеет смысл числа белых шаров среди
с таким распределением имеет смысл числа белых шаров среди 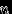 шаров, выбранных наудачу и без возвращения из урны, содержащей
шаров, выбранных наудачу и без возвращения из урны, содержащей 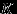 белых шаров и
белых шаров и 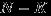 не белых.
не белых. Таблицу распределения
 читатель может нарисовать самостоятельно.
читатель может нарисовать самостоятельно. Заметьте, что со всеми этими распределениями мы уже хорошо знакомы.
Но распределения случайных величин далеко не исчерпываются дискретными распределениями. Так, например, если точка бросается наудачу на отрезок [0,1], то можно задать случайную величину, равную координате этой точки. Но число значений этой случайной величины не счетно, так что ее распределение дискретным не является. Да и вероятность этой случайной величине принять каждое из своих возможных значений (попасть в точку) равна нулю. Так что не только таблица распределения не существует, но и соответствие «значение величины
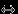 вероятность его принять» ничего не говорит о распределении случайной величины.
вероятность его принять» ничего не говорит о распределении случайной величины. Какими же характеристиками еще можно описать распределение?
