Основные виды случайных величин

Вид материала

Лекции

Подобный материал:

• Лабораторная работа №2 Тема: Формирование выборки случайных чисел, распределенных, 151.75kb.
• Т. И. Алиев Учебно-исследовательская работа И1 Исследование, 295.14kb.
• Основные виды случайных величин, 49.77kb.
• Задачи по теории вероятностей и математической статистике, 57.05kb.
• Программа по дисциплине теория вероятностей и математическая статистика, 95.11kb.
• Тем Введение в моделирование, 34.05kb.
• Функция распределения. Плотность распределения. Основные параметры непрерывных случайных, 7.05kb.
• Методика построения гистограммы и кривой эмпирического распределения 9 Статистические, 26.28kb.
• Числовые характеристики случайных величин, 50.29kb.
• Закон больших чисел и центральная предельная теорема и их роль в природе, технике, 35.67kb.

К лекции № 9


Основные виды случайных величин


9.1. Распределение ²


Пусть случайные величины X_i независимы и распределены по одному и тому же нормальному закону с параметрами a=0 и =1. Т. е. плотность распределения имеет вид



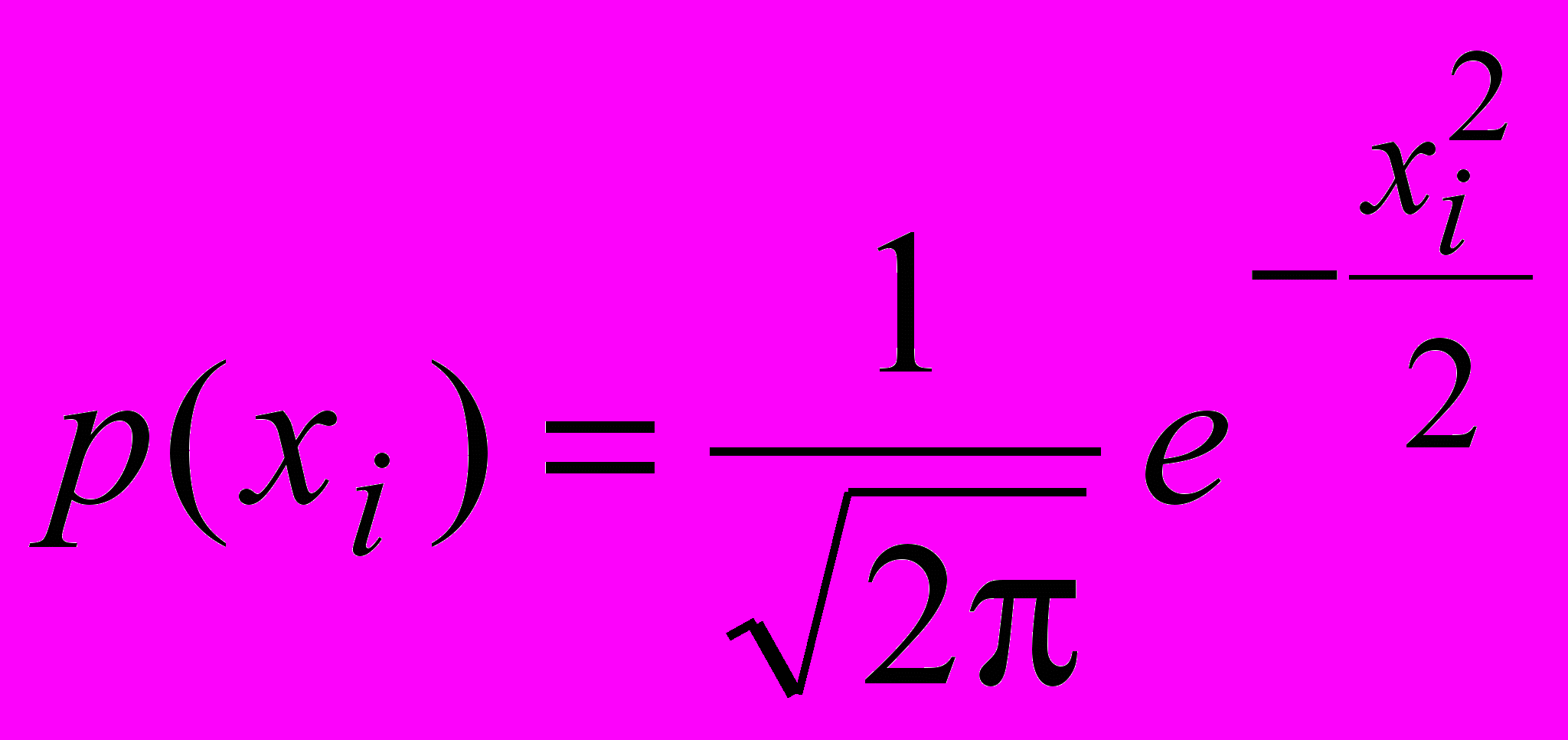
Случайная величина равная



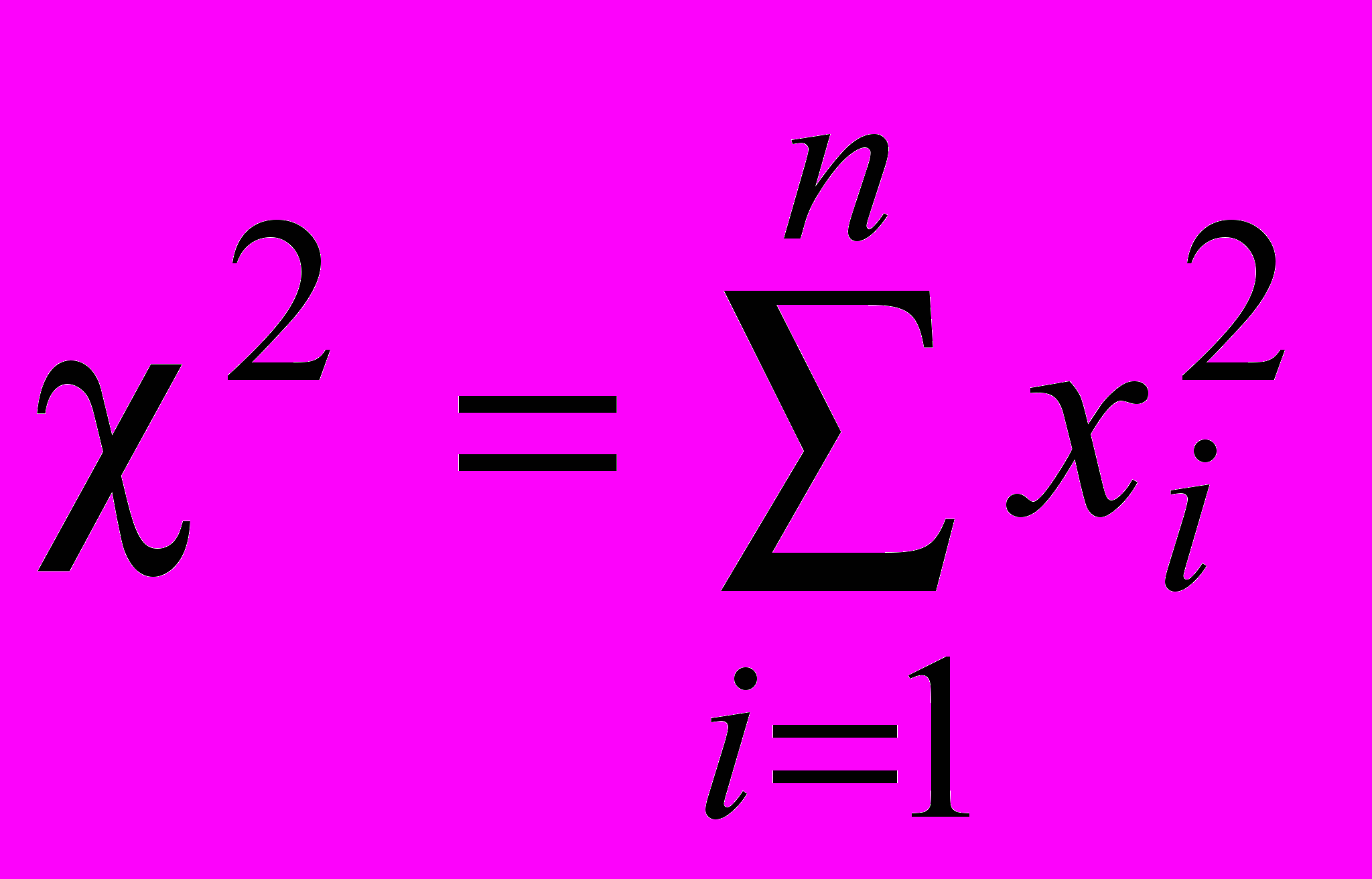
называется распределенной по закону ². Найдем ее функцию распределения K_n(x) и плотность распределения k_n(x) этой величины. Так как величины независимы, то плотность распределения системы равна



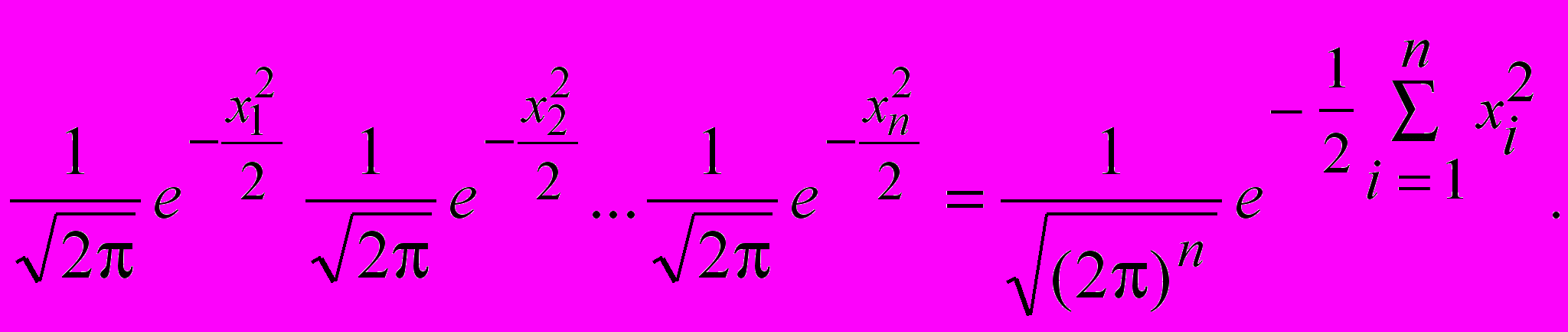
Функция распределения K_n(x) равна

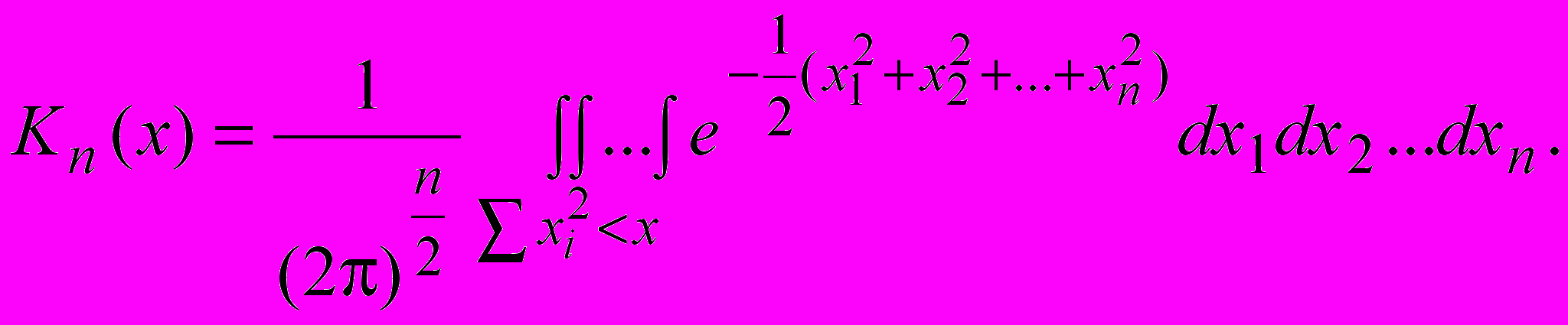при x>0.

Найдем приращение функции. С точностью до бесконечно малых выше первого порядка



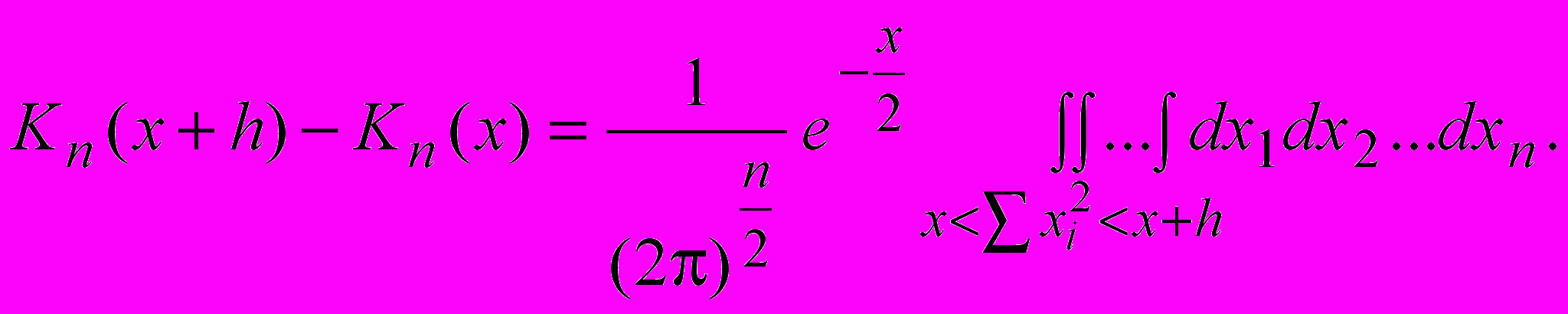
Выражение, стоящее под знаком интеграла, - это объем n-мерного шарового слоя с внутренним радиусом 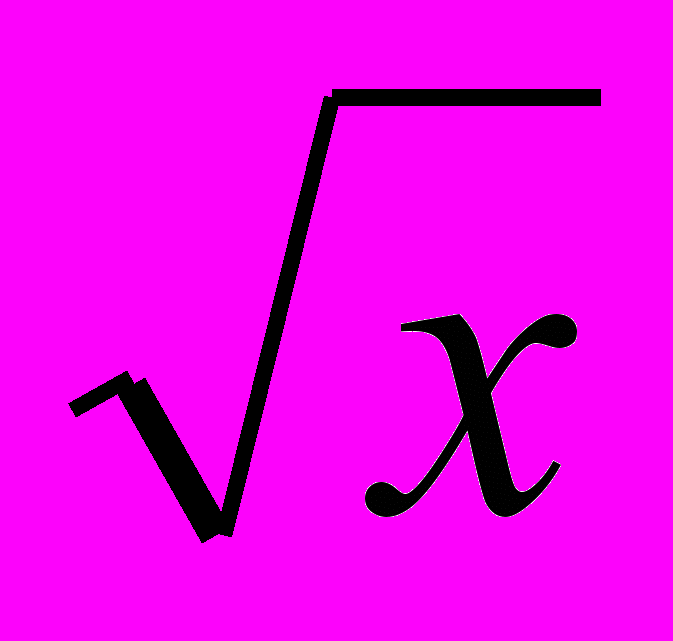и наружным радиусом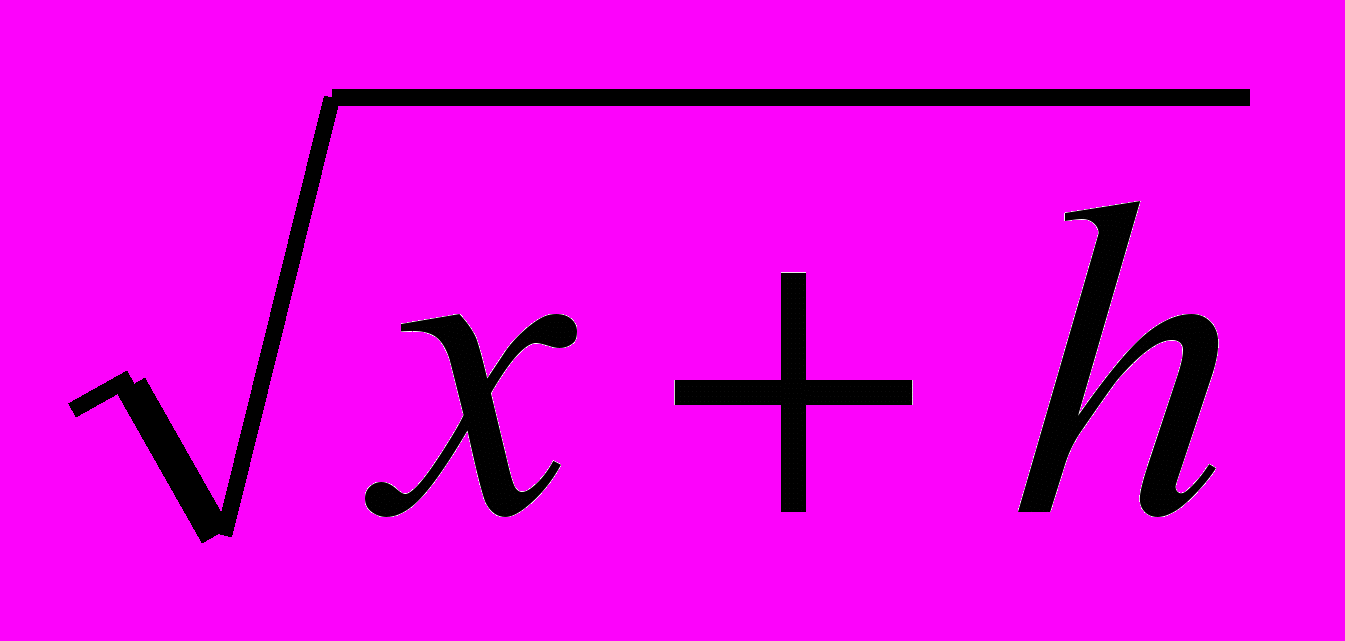. Обозначим V_n(R) - объем n-мерного шара радиуса R. Из соображений размерности ясно, что

V_n(R)=C_n,1Rⁿ,

где C_n,1 - некоторая постоянная

Поэтому



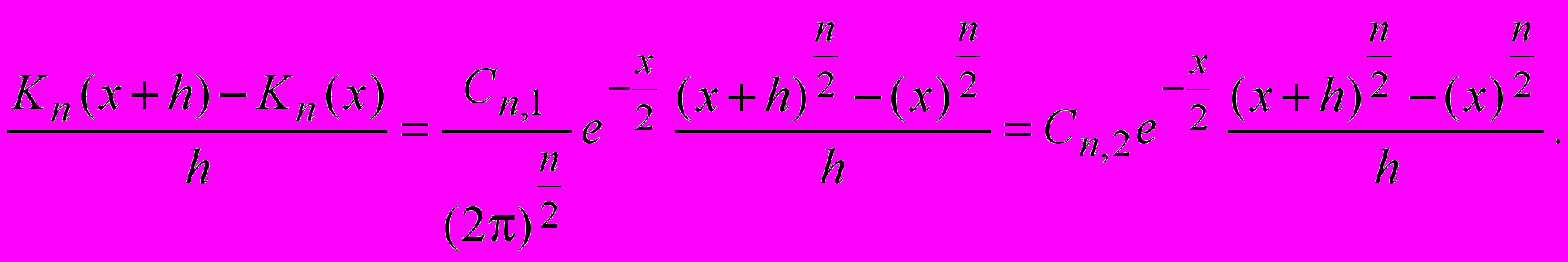
где C_n,2 - некоторая постоянная. После перехода к пределу при h0 в левой части плотность распределения, а в правой части последняя дробь даст производную выражения x^n/2. Получим



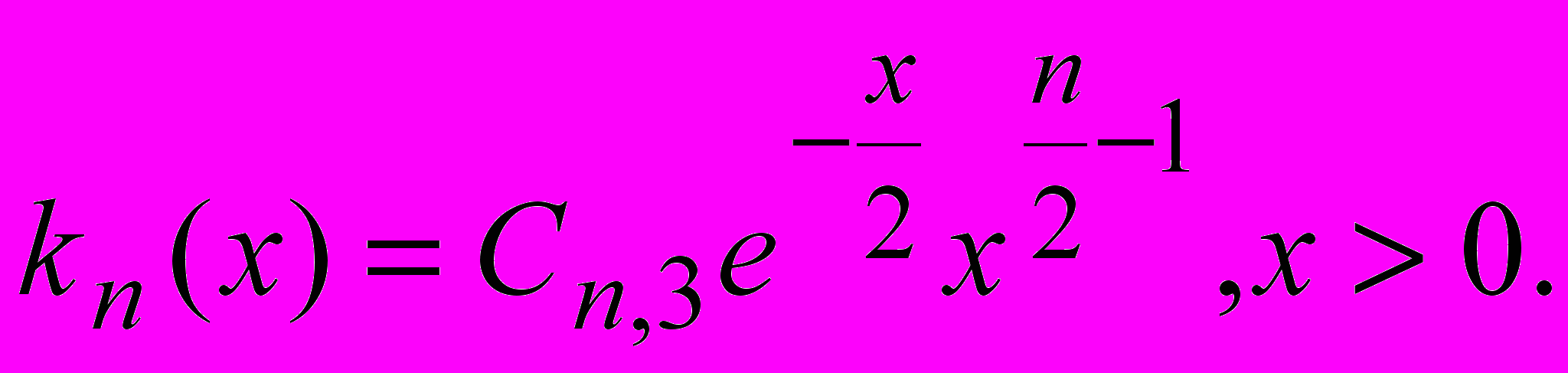
Для определения постоянной C_n,3 используем свойство



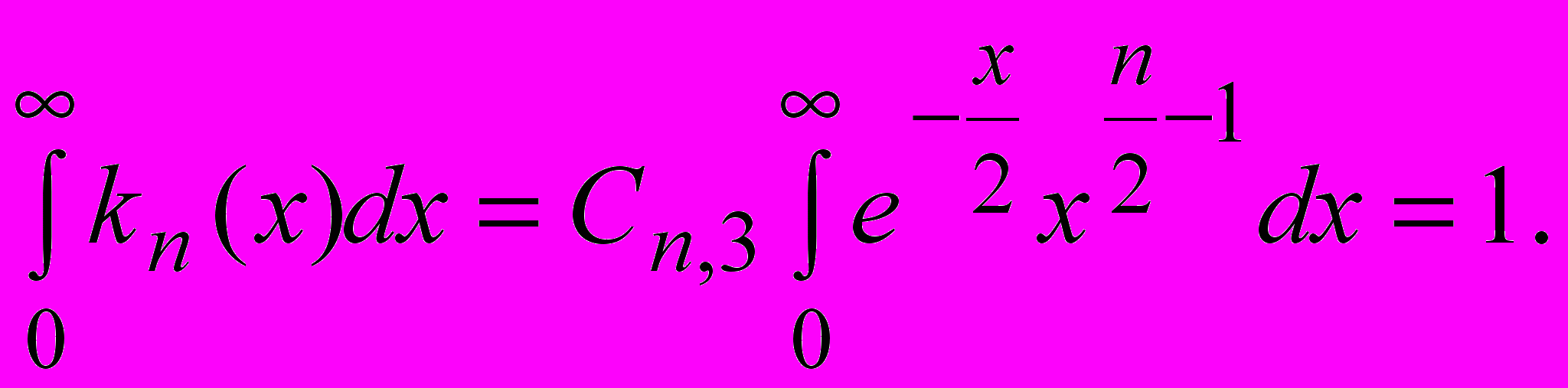
Введем замену u=x/2. Получим



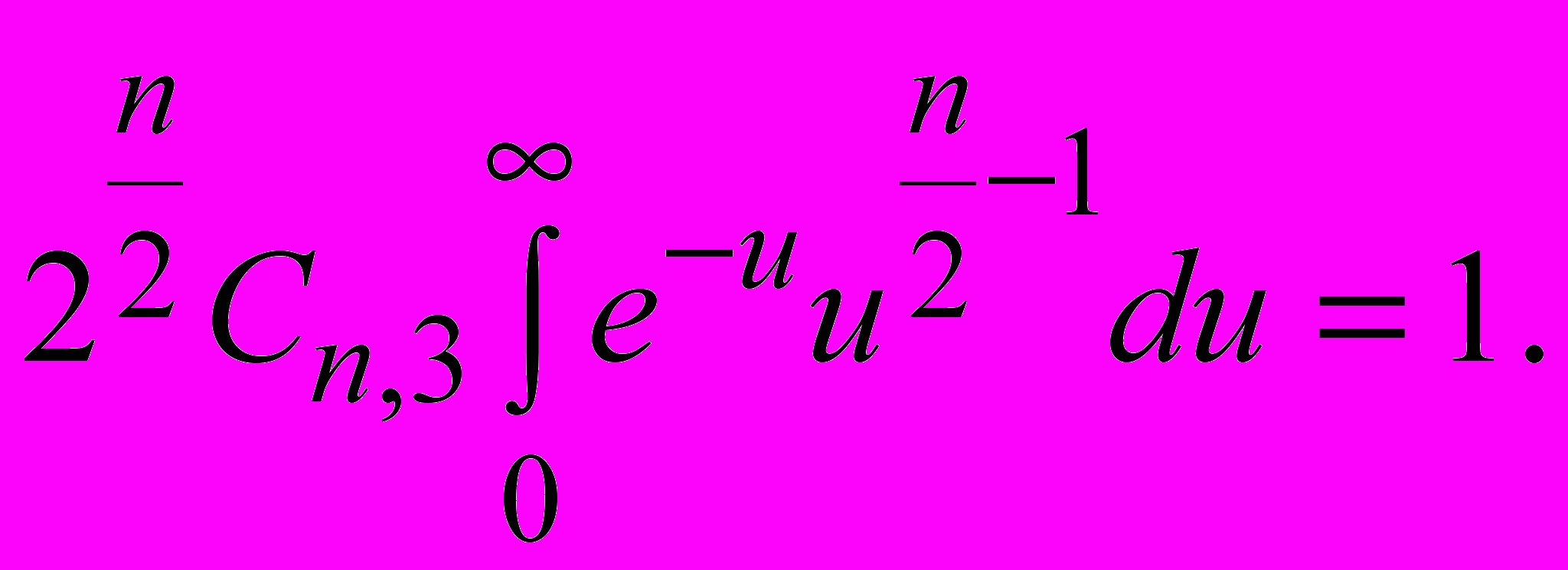
Интеграл вида



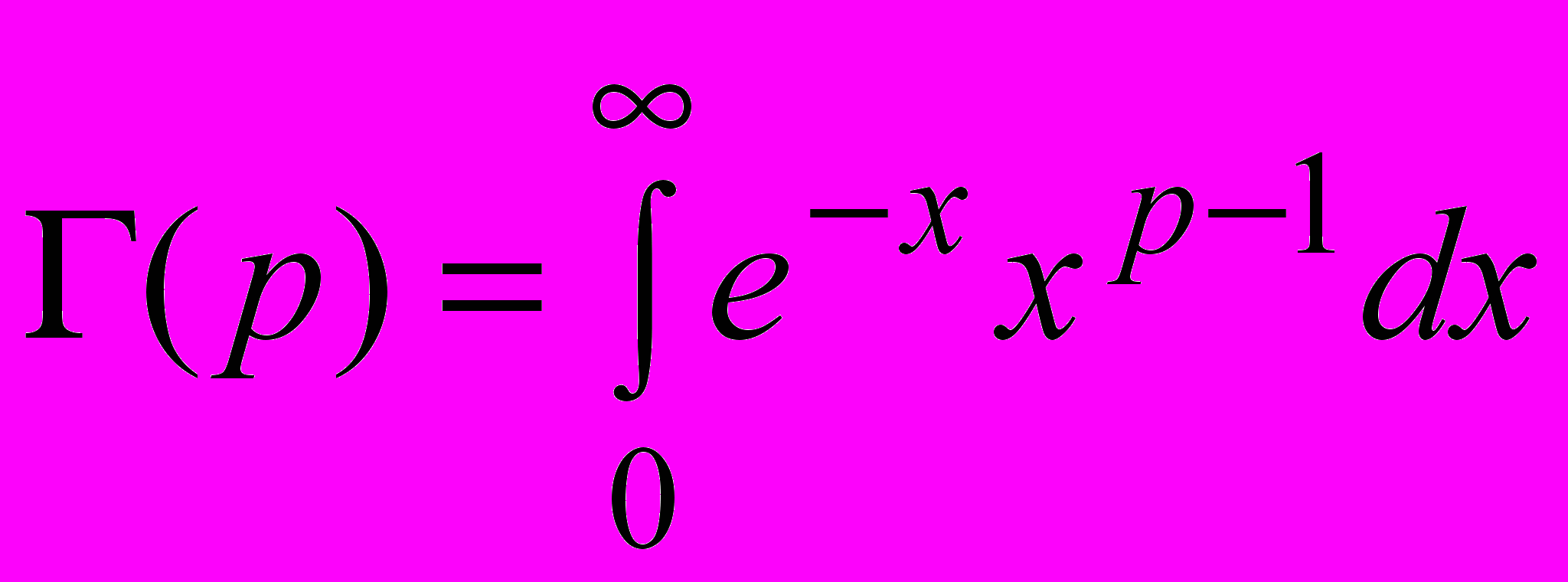
называется гамма-функцией. Поэтому



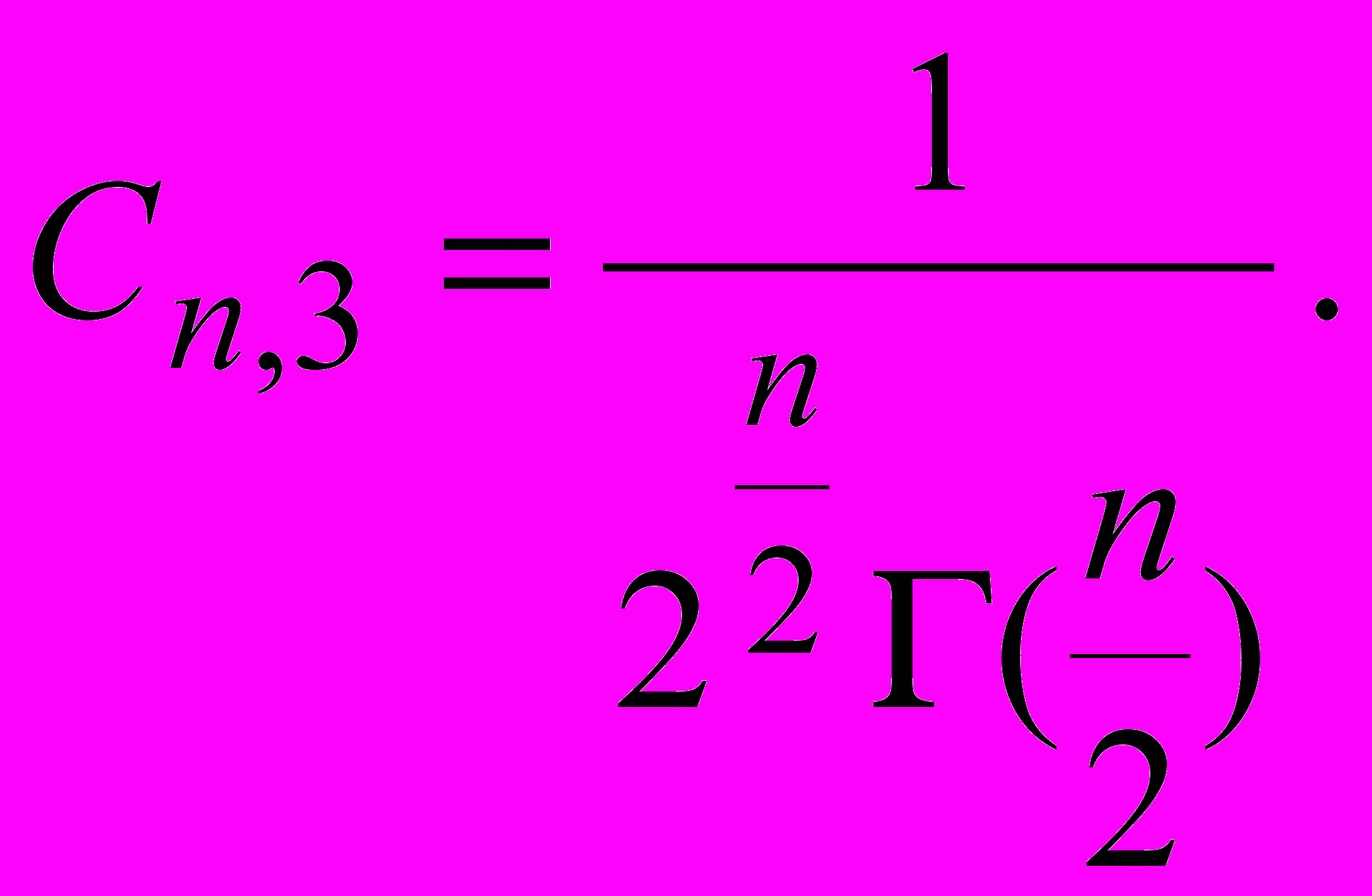
Окончательно



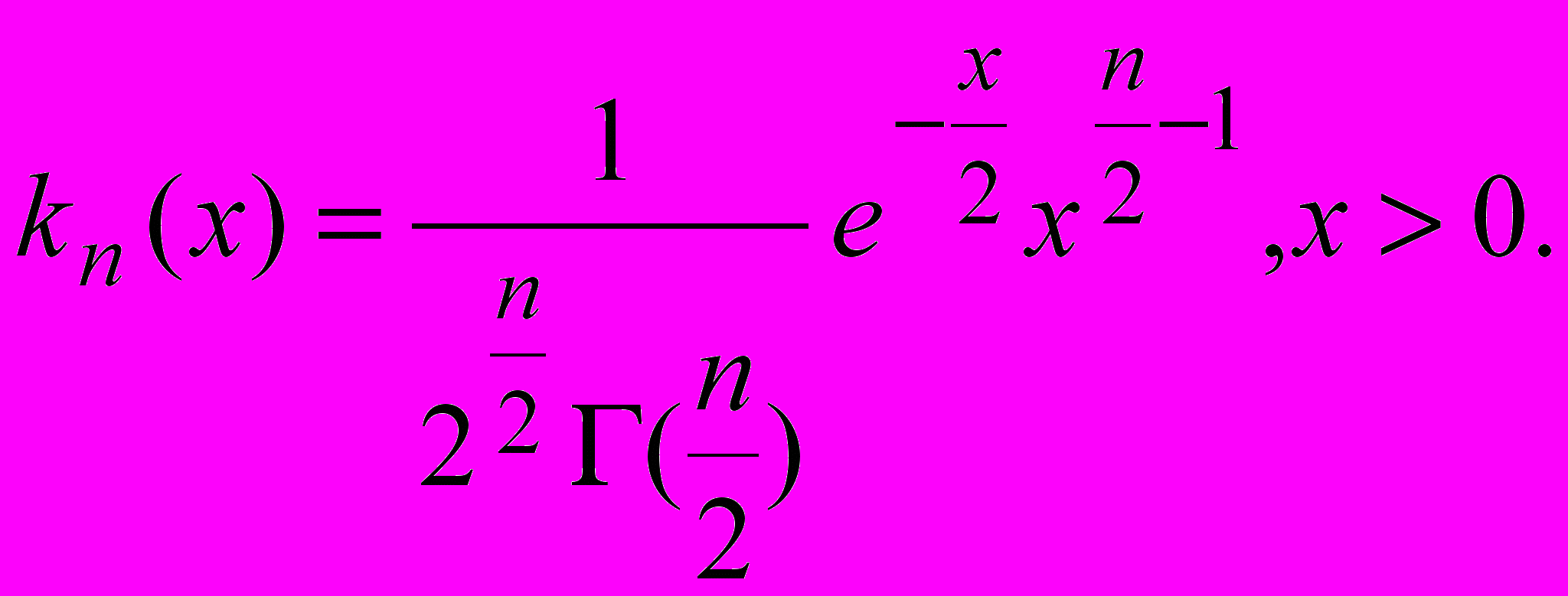
Этот закон распределения называется ² - распределением. Число n называется числом степеней свободы. Этот закон находит важные применения при статистических исследованиях. По закону распределения ² распределена так называемая статистическая дисперсия, т. е. статистическая оценка дисперсии.


9.2. Распределение Стьюдента


Рассморим случайную величину вида



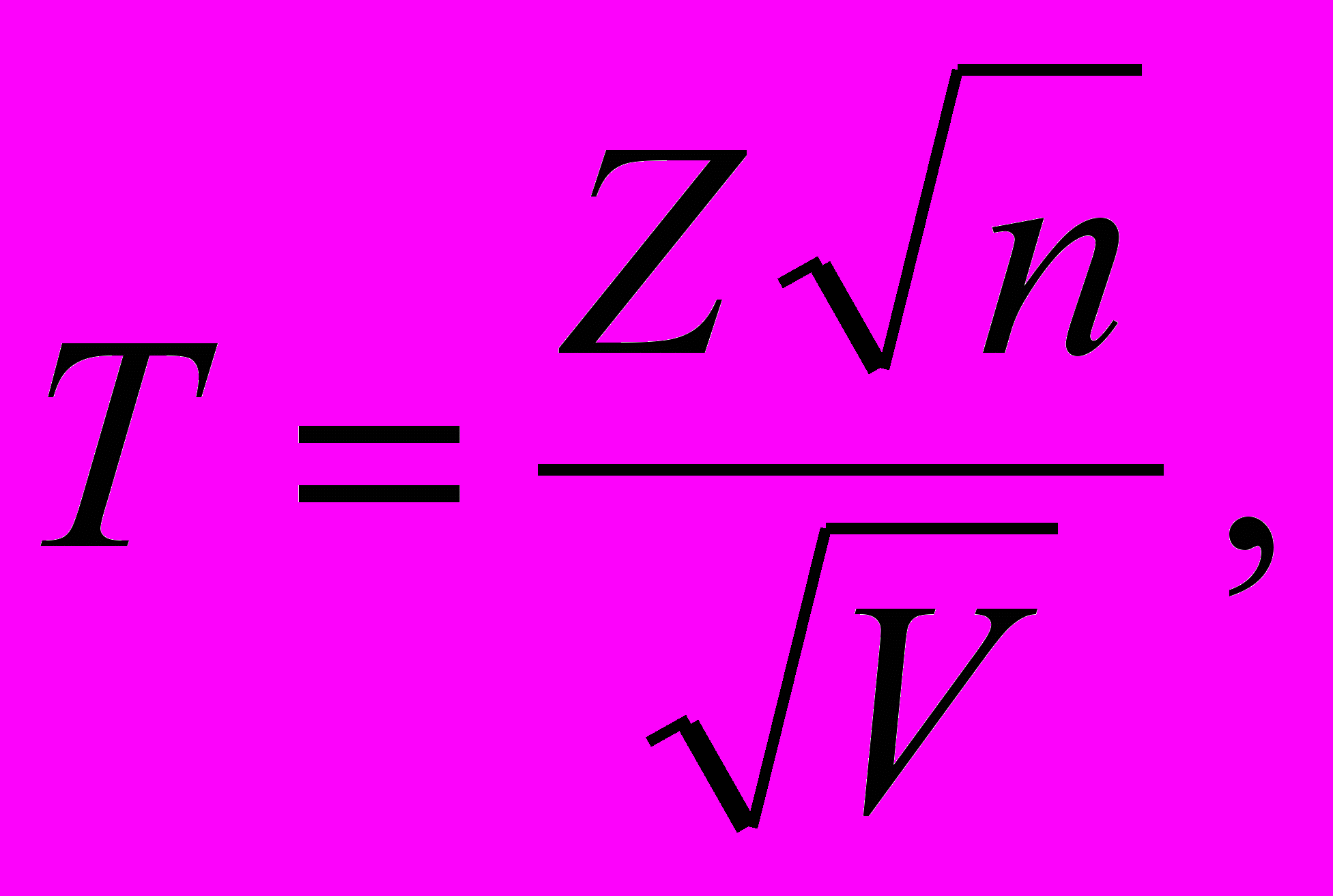
где случайные величины Z и V независимы, Z распределена по нормальному закону с параметрами a=0 и =1, а V по закону ² с n степенями свободы. Тогда плотность распределения случайной величины T имеет вид



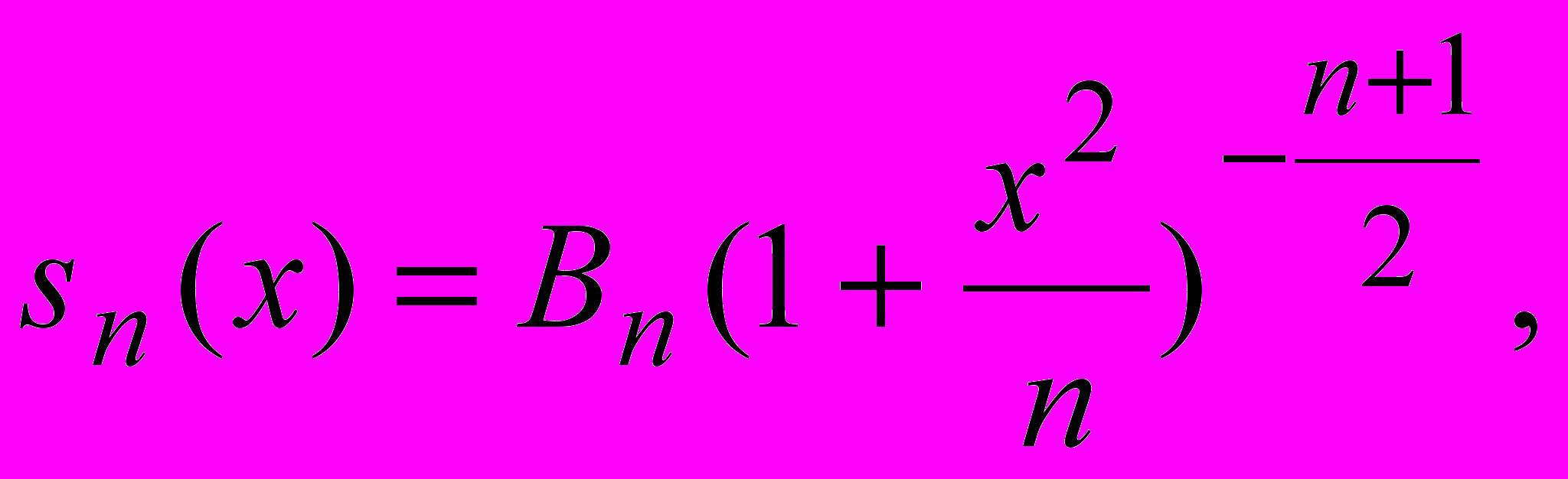
где



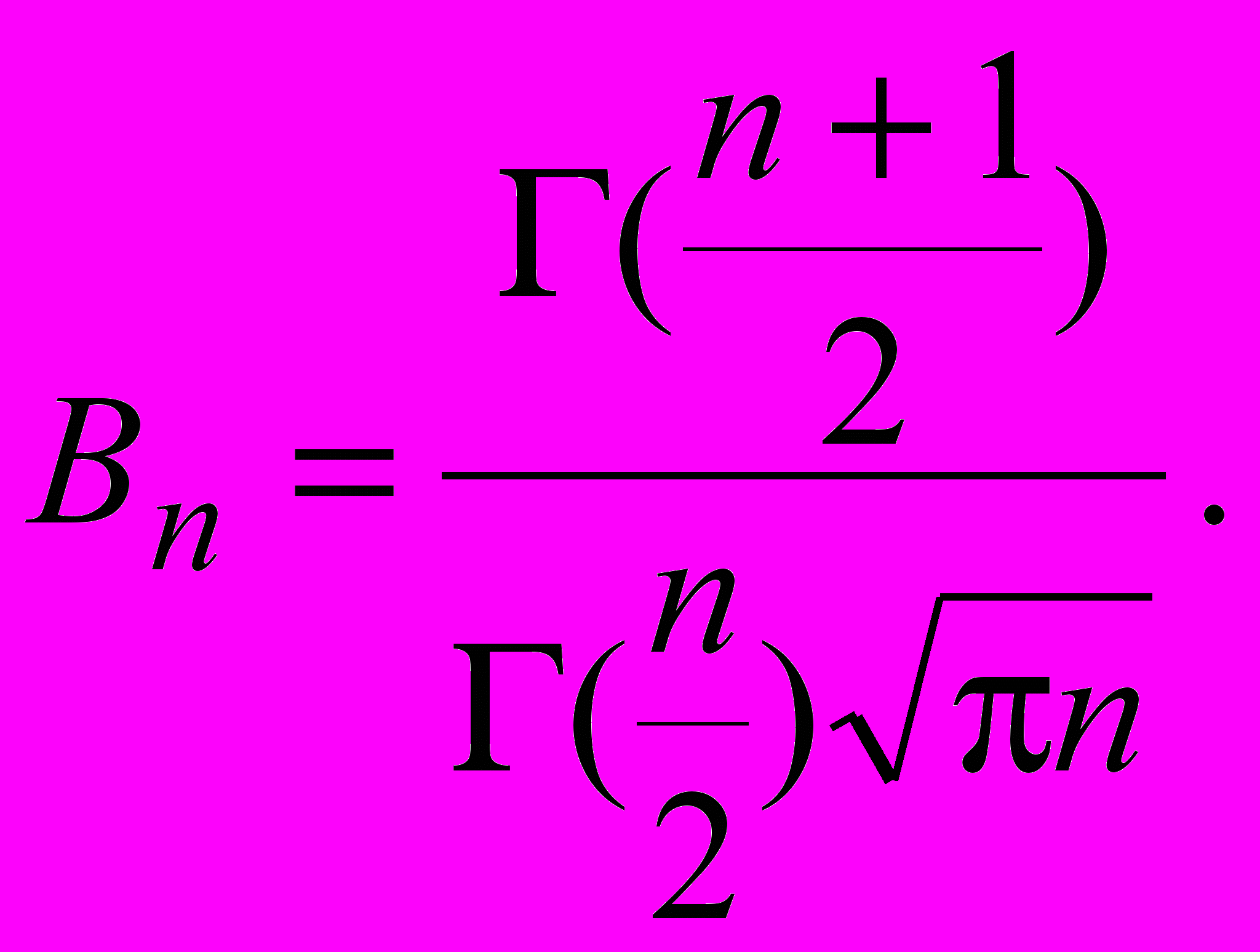
Вывод дан без доказательства. Этот закон распределения называется распределением Стьюдента. Отметим, что при больших n (n>50) закон распределения Стьюдента близок к нормальному закону распределения. Этот закон также находит важные применения при статистических исследованиях. По закону распределения Стьюдента распределено отношение статистического математического ожидания к статистическому среднеквадратическому отклонению.


9.4. Распределение Фишера


Рассмотрим случайную величину вида



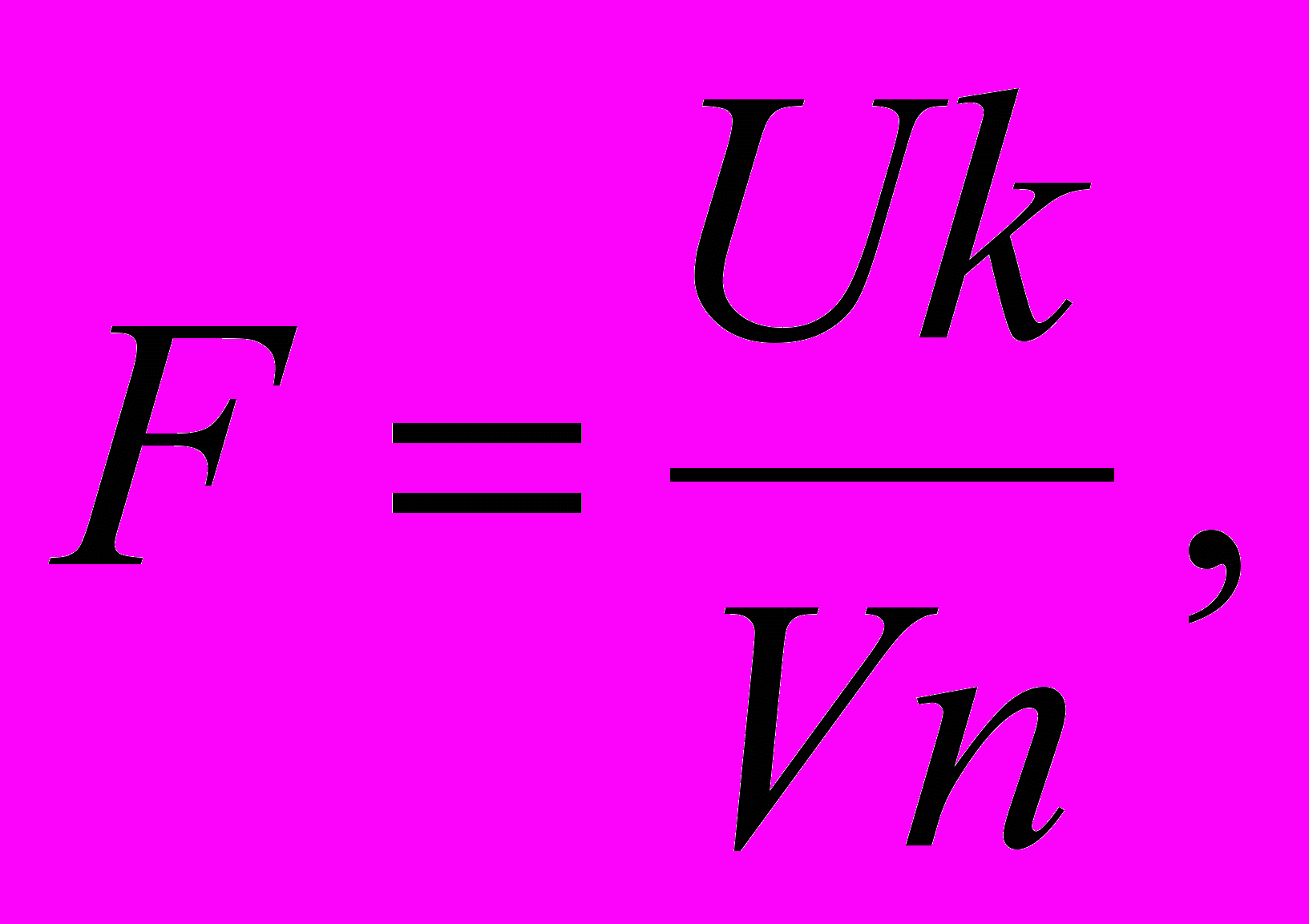
где случайные величины U и V независимы и распределены по закону ² с n и k степенями свободы. Тогда плотность распределения случайной величины F имеет вид



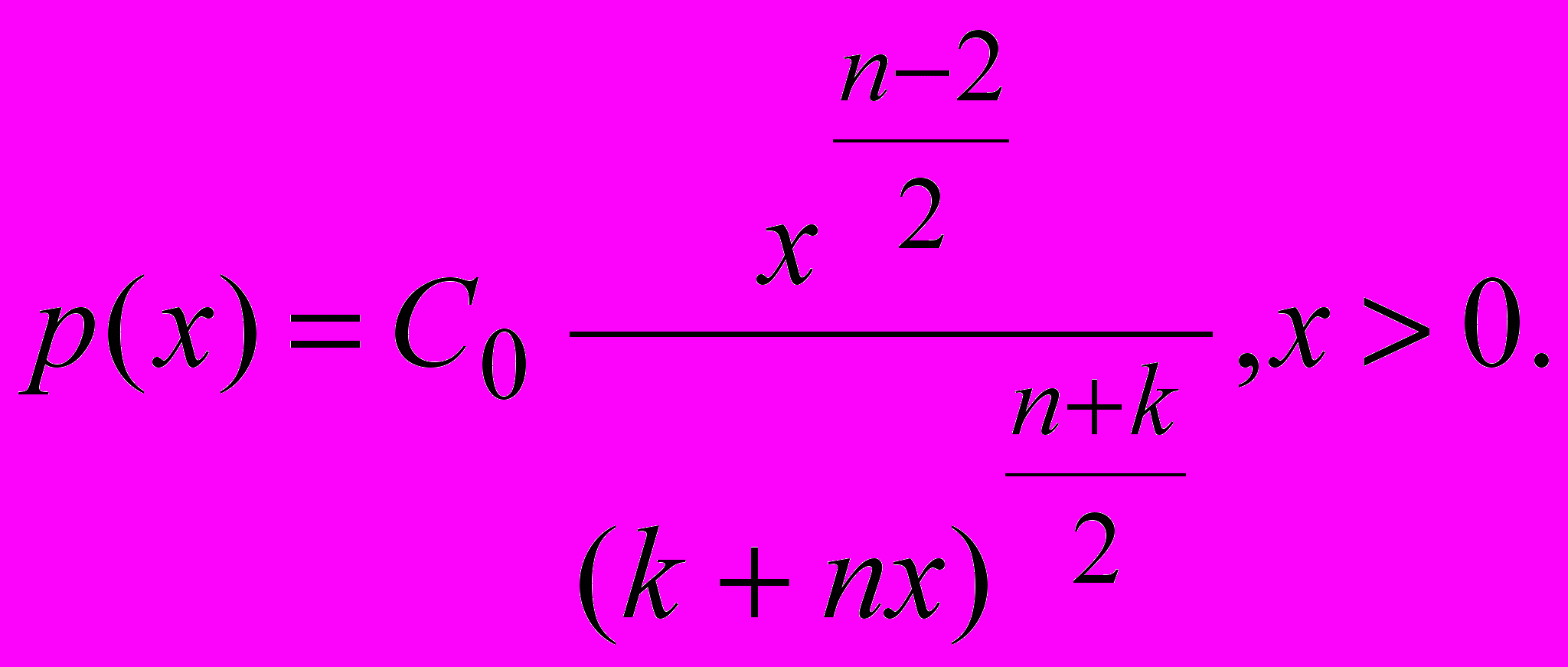
Вывод дан без доказательства. Этот закон распределения называется распределением Фишера с k и n степенями свободы Этот закон также находит важные применения при статистических исследованиях. По F-распределению распределено отношение статистических дисперсий сравниваемых величин.

Для всех распределений приведены таблицы, по которым находятся соответствующие вероятности.