Московский институт радиотехники, электроники и автоматики

Вид материала

Исследование

Подобный материал:

• Московский Институт Радиотехники, Электроники и Автоматики (технический университет), 57.53kb.
• Синергетика, 150.13kb.
• «Информация», 313.2kb.
• «генотип», 408.58kb.
• Диалектика, 172.21kb.
• Искусственный интеллект, 12.42kb.
• «История Музыкального Воспитания», 184.97kb.
• Пространство и время, 76.07kb.
• "Этика" Преподаватель: Шемакин, 261.25kb.
• Радиотехники, электроники и автоматики, 590.44kb.

Московский институт радиотехники, электроники и автоматики

Кафедра ИТС

СИСТЕМА МАССОВОГО ОБСЛУЖИВАНИЯ

Студент: Кокин Ю.С.

Группа: ИБ-1-96


Москва, 2001 г.


МАССОВОГО ОБСЛУЖИВАНИЯ СИСТЕМА — одна из возможных математических формализации реальных систем технического, производственного, экономического или био­логического характера, осуществляемая с целью исследования работы системы и на­хождения наиболее рационального режима ее функционирования. М. о. с.— основной объект изучения массового обслуживания теории. Наибольший интерес с практической и теор. точки зрения представляет изучение т. о. вероятностных М. о. с., в функционировании которых принимают участие различные веро­ятностные факторы: случайные величины, си­стемы взаимно зависимых случайных величии, случайные процессы различной природы.

Исследование вероятностных М. о. с. пред­ставляет собой специфический раздел случай­ных процессов теории. Реальной системой, допускающей формализацию в виде М. о. с., является, напр., производственная станочная линия. Каждый станок такой линии можно рассматривать как обслуживающий прибор, выполняющий ту пли иную операцию обслу­живания. Поступления материалов, загото­вок, полуфабрикатов на линию извне обра­зуют совокупность входящих потоков системы. Время обработки детали на станке интер­претируется как время обслуживания. Запас заготовок, подлежащих обработке, образует очередь. Выходящими потоками М. о. с. яв­ляются потоки готовых деталей, прошедших обработку, отсев обракованных изделий, про­изводственные отходы. Группа станков, осу­ществляющих выполнение одной и той же производственной операции для различных деталей, образует м н о г о л и н е й н у ю М. о. с.

М н о г о ф а з н а я М. о. с.— это группа станков, последовательно выполняющих различные операции обработки одних и тех же деталей. Вынужденные перерывы в производ­ственном процессе и в снабжении рассматри­ваются как блокировка (см. Блокировка обслу­живания). Исследовать эту систему могут, напр., с целью определения таких значений параметров системы, при которых достигается максимум выпускаемой продукции за фикси­рованное время или минимум ожидаемых за­трат при выпуске заданного к-ва продукции.

Функционирование М. о. с. сопряжено с по­ступлением извне или возникновением внутри системы определенных требований, вызовов, сообщений (абонентов), прохождением их че­рез систему, расщеплением па несколько но­вых требований или рекомбинацией несколь­ких требований в одно, выходом требований из системы. Процесс поступления или возник­новения абонентов носит характер потока слу­чайного. М. о. с. может обладать одним или несколькими однородными или неоднородны­ми, взаимно независимыми или зависимыми, равноправными или неравноправными входя­щим и случайными потоками.

Осн. элементом каждой М. о. с. служит т. п. обслуживающий механизм (прибор, линия, ка­нал) — функциональный элемент, осуществ­ляющий непосредственно операцию обслужи­вания требований (задержки во времени). В различных случаях М. о. с. может содер­жать только один обслуживающий механизм или мн-во их (конечное или бесконечное). Дли­тельность обслуживания требований (время обслуживания) — одна из существенных ха­рактеристик процесса обслуживания, про­текающего в системе. Длительности обслужи­вания различных требований могут быть по­стоянными (одинаковыми или различными для различных обслуживающих механизмов), слу­чайными (взаимно независимыми или зависи­мыми, распределенными по одному и тому же закону или по различным законам), управ­ляемыми (могут зависеть от состояний в дан­ный момент некоторых из элементов системы). Перемещение требований внутри системы от одних обслуживающих механизмов к другим происходит на основании спец. правил функ­ционирования системы, входящих в ее опи­сание.

Во многих М. о. с. происходит ожидание требований, поступивших к обслуживающему механизму в тот момент, когда последний .за­нят обслуживанием ранее прибывшего требо­вания. При этом образуется очередь требова­ний. Очередь может быть общей для всех об­служивающих механизмов системы или перед отдельными механизмами или их группами может формироваться отдельная очередь. Тре­бования, покидающие систему в процессе ее функционирования, образуют выходящий но­ток. В различных случаях системы могут иметь выходящие потоки полностью обслуженных требований, потоки частично обслуженных или совсем необслуженных требований (пото­ки потерь). Для потребностей практики часто необходимо изучать М. о. с., в которых об­служивающие приборы время от времени мо­гут выходить из строя. Встречаются также ситуации, когда отдельные входящие потоки системы периодически на некоторое время пе­рестают действовать — т. е. происходит блоки­ровка входов системы.

Для М. о. с. весьма существенна ее струк­тура. В понятие структуры М. о. с. включа­ется информация о том, сколько в системе об­служивающих механизмов каждого типа, о на­личии входящих и выходящих потоков, об их взаимной приоритетности, о возможности фор­мирования очередей перед определенными об­служивающими механизмами или их груп­пами, о путях перемещения требований внутри системы. Различают однолинейные и мпоголинейные системы, однофазные и многофазные (многоэтапные). Многолинейная система в отличие от однолинейной имеет несколько (конечное, или счетное, множество) обслуживающих механизмов, выполняющих однородные операции обслуживания, т. е. осуществляющих параллельное обслуживание. Требование считается обслуженным системой, если оно прошло обслуживание на одном из ее обслуживающих механизмов.

На рис. 1 схематически изображена много­линейная система обслуживания с общим входящим потоком и одной общей для всех обслуживающих механизмов очередью ожидающих требований. Прямоугольниками Л, В, С, ..., К представлены обслуживающие при­боры, кружками — ожидающие требования, сплошной стрелкой — входящий ноток, штри­ховыми стрелками — возможные пути дви­жения требований. Во многофазной М. о. с. обслуживающие механизмы выполняют раз­нородные операции обслуживания и осуществ­ляют последовательный процесс обслужива­ния. Требование считается полностью обслу­женным данной системой, если оно было полностью обслужено на каждой из ее фаз (этапов). Схематическое представление о та­кой системе дает рис. 2 (обозначения на нем та­кие же, как и на рис. 1).





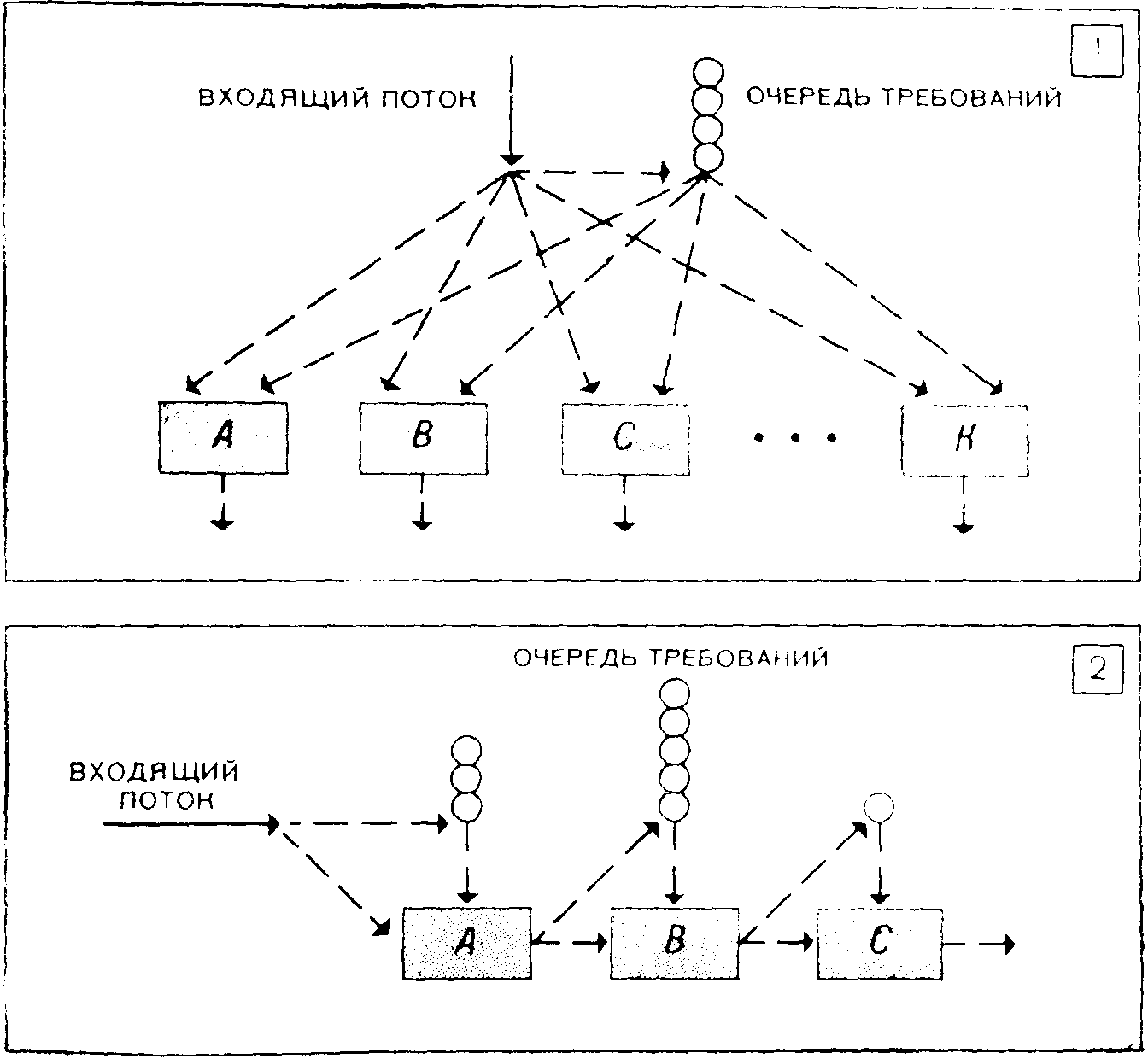
1. Схема многолинейной системы массового обслуживания.

2. Схема многофазной системы массового обслуживания.

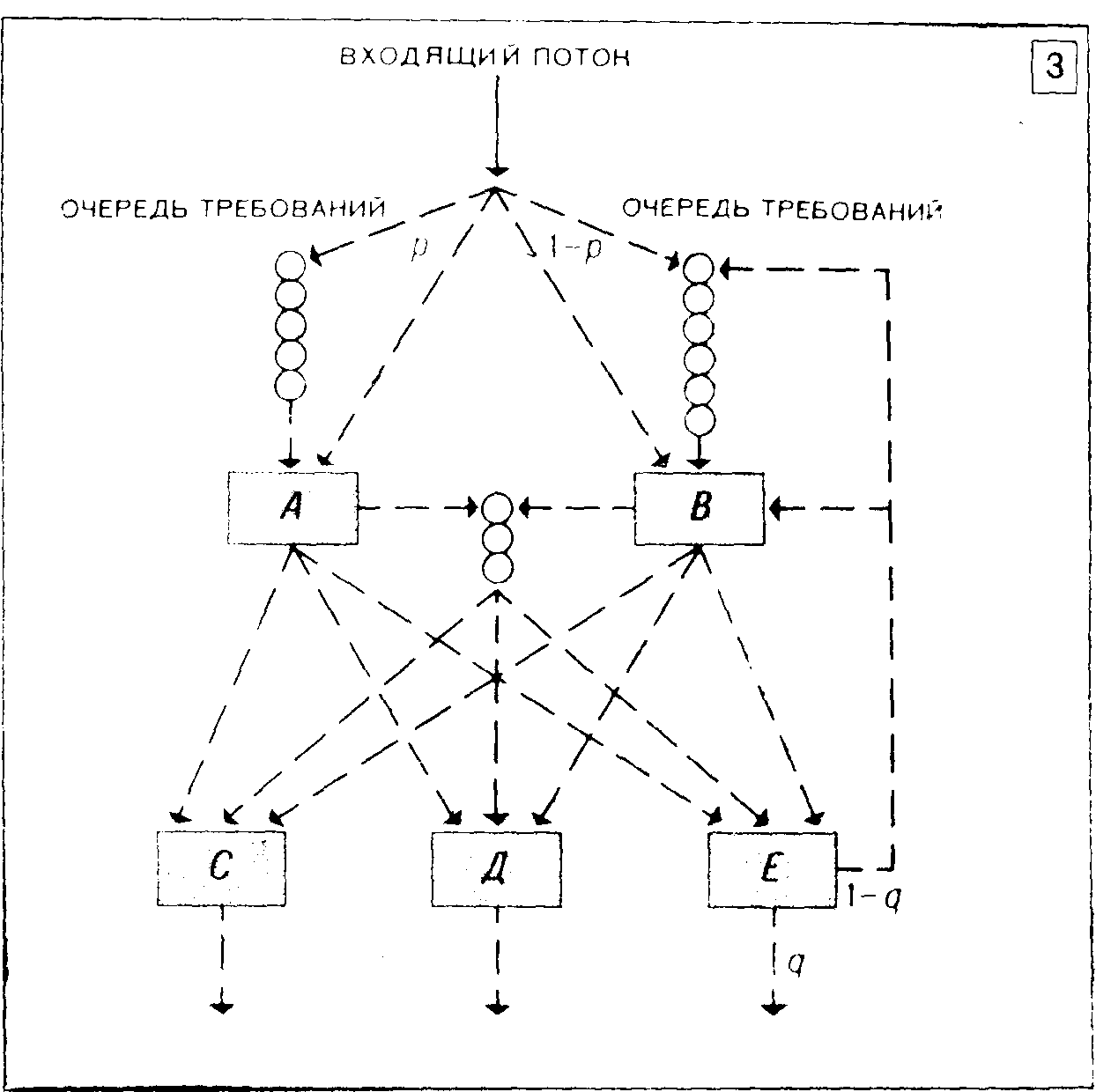
3. Схема сети массового обслуживания.


Перед каждой фазой формируется самостоя­тельная очередь. М. о. с., являющаяся систе­мой смешанного типа, т. е. обладающая в одно и то же время свойствами многолинейных и многофазных систем, а также иногда харак­теризуемая и усложненными связями других типов (напр., возможность для части требо­ваний проходить повторное обслуживание на некоторых фазах), наз. сетью массо­вого обслуживания. Схема одной из таких сетей приведена на рис. 3 (буквен­ные символы, проставленные около некото­рых стрелок, означают вероятности направле­ния требования по данному пути). Некоторые М. о. с. обладают, напр., такими свойства­ми, как ограничение времени ожидания или времени пребывания в системе, блокировка обслуживания и входящего потока, резерви­рование запасных элементов и восстановле­ние вышедших из строя. Такие свойства по­зволяют причислять, в принципе, каждую М. о. с. к тому или иному классу систем. Рас­смотрим подробнее некоторые наиболее важ­ные классы таких систем.

М. о. с. с ожиданием — система, в ко­торой предусматривается возможность фор­мирования очереди требований, ожидающих обслуживания. Это самый распространенный и общий тип М. о. с. Наиболее простой част­ный случай такой системы имеет место, когда при функционировании системы происходит образование т. н. простой очереди, когда все поступающие требования однородны, допуска­ется их накопление в очереди в любом к-ве, требования выбывают из очереди для об­служивания строго в порядке очередности их поступления в очередь. Несколько более сложным является принцип формирования очереди с приоритетами. При этом каждому поступившему требованию ставится в соответ­ствие определенная характеристика — пока­затель приоритетности. Требование претен­дует на право постановки в определенное место очереди согласно значению его показателя приоритетности. Иногда требования, ожидающие в очереди, должны быть охарак­теризованы рядом числовых показателей. Та­кая ситуация наиболее типична для задач уп­равления, при решении которых производится выбор требования из очереди на основании многих его характеристик. Примеры реальных М. о. с. с ожиданием: склад, отпускающий продукцию по заявкам, система автомати­зированной обработки поступающей инфор­мации на электронных или перфорационных машинах, морской порт, выполняющий обра­ботку прибывающих судов.

М. о. с. с ограничениями — систе­ма, функционирование которой обусловлено определенными ограничениями, касающимися различных ее характеристик и показателей требований, проходящих через систему. Чаще всего ограничения налагают на длину очере­ди, время ожидания требования и на время его пребывания в системе. При ограничении длины очереди с помощью постоянной или случайной величины требования, прибывшие в систему и заставшие там очередь предельно допустимой длины, теряются и не проходят обслуживания. При ограничении, налагаемом на время ожидания, происходят потери тре­бований, которые, пробыв в очереди предель­но допустимое время, не дождались начала обслуживания. Если в алгоритме функ­ционирования М. о. с. предусмотрено ограни­чение, накладываемое на время пребывания требования в системе, то требование покидает систему всякий раз, когда время с момента его прибытия в систему достигнет максималь­но возможной величины. Это может произойти либо в момент, когда требование обслужива­ется (происходят потери частично обслуженных требований), либо когда он ожидает в очереди (потери полностью не обслуженных требова­ний). На практике М. о. с. с ограничениями весьма распространены. Это, напр., устрой­ства для обработки информации, обладающие памятью конечного объема, склады ограничен­ной емкости, счетчики для регистрации эле­ментарных частиц, которые вызывают све­чение экрана только на протяжении опреде­ленного времени после их попадания и т. д. Исследования М. о. с. с ограничениями имеют для практики весьма важное значение, т. к. дают возможность судить о способности си­стемы работать без потери информации или допускать такую потерю в заданных пределах.

М.о.с. с потерями — системы, в ко­торых не допускается образование очереди пе­ред обслуживающими механизмами. Системы такого типа являются частными случаями си­стем с ограничением, когда длина очереди требования ограничена величиной нуль. На практике — это системы обработки информа­ции без ассоциативной памяти, в частности, системы автомат, телефонных станций. Осн. интерес при изучении М. о. с. с потерями пред­ставляет определение доли всех поступивших требований, которым удалось пройти обслу­живание.

М.о.с. с резервированием — си­стемы, в которых предполагается возможность выхода из строя обслуживающих механизмов и замены неисправных механизмов резервны­ми. Для систем этого типа характерны сле­дующие понятия (в общем случае — это слу­чайные величины): время безотказной работы (продолжительность жизни) обслуживающего механизма, время восстановления неисправ­ного элемента, наличный запас резервных эле­ментов, длина очереди неисправных элемен­тов, ожидающих восстановления. Различают нагруженный и ненагруженный резервы. Эле­менты нагруженного резерва в любой момент готовы к использованию для обслуживания требований. Чтобы вышедший из строя эле­мент заменить элементом из ненагруженного резерва, последний необходимо предваритель­но перевести из ненагруженного состояния в нагруженное. Издержки содержания элемен­та в нагруженном состоянии, как правило, больше издержек содержания его в ненагру­женном состоянии. М. о. с. с резервированием широко применяют в теории надежности. Фор­мализация реальных систем в виде М. о. с. с резервированием позволяет наиболее подроб­но отразить существо функционирования си­стем с ненадежными элементами. В частности, это относится к различным электронным схе­мам. Круг М. о. с. с резервированием достаточно обширный и многообразный. Для неко­торых наиболее часто встречающихся М. о. с. введено систему сокращенных обозначений. Каждое обозначение состоит из трех символов. Первый характеризует входящий поток, вто­рой — время обслуживания, третий — число обслуживающих приборов. Обозначение стан­дартное: М — Пуассона поток, иди показа­тельное время обслуживания; Е — поток Эрланга или время обслуживания; G — ре­куррентный поток; GI — независимые оди­наково распределенные длительности обслу­живания. Так, М \ Е | S означает многолинейную М. о. с. с S приборами, пуассоновским входящим потоком и эрланговским вре­менем обслуживания.

В большинстве случаев никакое указание на принадлежность М. о. с. к тому или дру­гому классу систем или о наличии у системы тех или иных особенностей не определяет пол­ностью ни структуры системы, ни алгоритма ее функционирования. Для этого необходимо достаточно подробное словесное или матем. описание системы. Описание системы незави­симо от формы его задания должно содержать сведения о вероятностных факторах, влияю­щих на систему. Одним из наиболее универ­сальных и самых распространенных методов матем. описания М. о. с., являющимся одно­временно и методом матем. исследования таких систем, служит аппарат вероятностных мар­ковских процессов. При этом в каждый момент времени система может быть охарактеризова­на с помощью некоторого вектора, компонен­тами которого служат временные характери­стики системы. Изменение значений этого век­тора во времени определяют с помощью либо стохастической матрицы вероятностей пере­хода, либо некоторой системой ур-ний: раз­ностных, дифф., интегр., интегро-дифференциальных, стохастических и т. д. Распростра­ненными методами решения таких ур-ний и получения окончательных результатов иссле­дования М. о. с. служат методы операцион­ного исчисления, особенно метод производя­щих ф-ций и интегр. преобразований.

При исследовании достаточно сложных М. о. с., для которых марковский вектор со­стояний имеет большую размерность, приме­нение аппарата марковских процессов в чис­том виде становится затруднительным. В этих случаях приходится применять другие, более тонкие методы описания и исследования си­стем. Одним из таких методов является метод вложенных цепей Маркова, заключающийся в рассмотрении состояний системы не во все моменты времени ее функционирования, а лишь в определенные моменты, когда компо­ненты марковского вектора состояний, инте­ресующие исследователя, образуют Маркова цепь. При описании и исследовании М. о. с. успешно применяется такой совершенный со­временный метод, как метод полумарковских процессов.

Во многих случаях возникает необходимость при описании системы учитывать изменение размерности марковского вектора состояний в процессе функционирования М. о. с. При этом бывает удобно пользоваться аппаратом марковских процессов. Задание такого про­цесса обычно осуществляется с помощью век­тора, одна из компонент которого является целочисленной и показывает размерность со­стояния системы в данный момент времени. Из других методов описания и исследования систем, применяемых при изучении М. о. с., следует указать на процессы с дискретным вмешательством случая, процессы, управляе­мые марковской цепью, управляемые полумарковские процессы и т. д. Если исследуемая система настолько сложна по своей структуре и алгоритму функционирования, что изучать ее всеми перечисленными аналитическими ме­тодами затруднительно, прибегают к методам статистического моделирования (см. Монте-Карло метод) с использованием ЭВМ.

При исследовании М. о. с., особенно систем с ожиданием, весьма существенным является вопрос о существовании для системы стацио­нарного режима функционирования, т. е. во­прос о возможности установления для системы со временем такого устойчивого равновесия состояний, при котором каждому состоянию системы из определенного мн-ва состояний соответствует определенная, не изменяющаяся в дальнейшем частота появления. Для одних и тех же М. о. с. в зависимости от значений параметров системы стационарный режим мо­жет либо существовать, либо не существовать. Условия существования стационарного режи­ма М. о. с. обычно могут быть записаны в виде систем неравенств и равенств относительно параметров системы и моментов случайных величин, влияющих на ее работу. Определе­ние условий существования стационарного режима — один из важных этапов исследова­ния М. о. с. Для его осуществления обычно применяются различные эргодические теоре­мы вероятностей теории.

В зависимости от задач, стоящих перед ис­следователем, целью исследования может быть вычисление того или иного неслучайного функ­ционала от характеристик системы Чаще всего таким функционалом оказываются показатели pacпределений вероятностей определенных характеристик системы (напр.. длины очере­ди, времени ожидания, периода занятости и т. д.). Если исследование носит оптимиза­ционный характер, вычисляемый функционал имеет вид целевой функции, отвечающей вы­бранному критерию эффективности системы. Оптимизация М. о. с. заключается в опреде­лении значений параметров системы, ее струк­туры или таких алгоритмов функциониро­вания, при которых целевая ф-ция принимает минимальное пли максимальное значение. Эту задачу иногда удастся выполнить, применяя методы линейного, нелинейного, динамиче­ского или эвристического программирования.


Система массового обслуживания (МОС) может быть открытой и замкнутой. Т.е. число требований может быть ограничено условиями в МОС, а может быть случайным и неограниченным. Но в том и другом случае система берет эти требования из окружающей среды, а после обслуживания или отказа от него возвращает в среду.

При многократном проведении эксперимента можно выявить закономерности и получить средние величины обслуженных требований. Если полученные результаты не удовлетворяют эксперта, то надо подстраивать систему. В систему массового обслуживания добавляется субъект системы - эксперт. Данная система – синергетическая, поскольку она самоорганизуется и эволюционирует до оптимальных показателей средних величин. По определению синергетической системы


БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Энциклопедия Кибернетики. Под ред. В.М. Глушкова. Киев, 1975 г.
   
2. Синергетические системы .Конспект лекций студента Кокина Ю.С. Преподаватель: Шемакин Ю.И. Рукопись. М., МИРЭА, 2001 г.