Шайтанова Лидия Михайловна, к т. н., доцент, доцент кафедры «Экономика и бухгалтерский учет» Омского института (филиала) ргтэу учебно-методический комплекс
| Вид материала | Учебно-методический комплекс |
| 9. Тесты для самоконтроля |
- Норышева Рита Александровна, к биол н., доцент кафедры «Торговое дело» Омского института, 470.34kb.
- Костарев Сергей Владимирович д ф. н., доцент, профессор кафедры «Менеджмент и маркетинг», 270.35kb.
- Ботов Михаил Иванович, к т. н., доцент, профессор ргтэу, Елхина Валентина Дорофеевна,, 622.56kb.
- Колущинская Оксана Юрьевна, ст преподаватель кафедры «Менеджмент и маркетинг» Омского, 566.62kb.
- Васильев Владимир Вениаминович Допущено Редакционно-издательским советом Омского института, 1786.57kb.
- Учебно-методический комплекс Для студентов, обучающихся по специальности 080507 «Менеджмент, 677.59kb.
- Баранников Александр Лукьянович, кандидат технических наук, доцент, доцент кафедры, 853.95kb.
- Баранников Александр Лукьянович, кандидат технических наук, доцент, доцент кафедры, 798.96kb.
- Кутыркин Александр Борисович, кандидат философских наук, доцент, доцент кафедры антикризисного, 304.07kb.
- Лепешкин Вячеслав Анатольевич, к э. н., доцент, доцент кафедры экономики и управления, 1452.03kb.
9. Тесты для самоконтроля
Тест 1
1. Необходимость учета фактора времени определяется:
а) инфляцией;
б) различными процентными ставками;
в) принципом неравноценности денег в различные моменты времени.
2. Фактор времени в финансовых вычислениях учитывается:
а) с помощью множителя затрат;
б) с помощью начисления процентов;
в) начальной суммой ссуды.
3. Процентами в финансовых расчетах называют:
а) наращенную сумму долга;
б) процентную ставку;
в) абсолютную величину дохода от предоставления денег в долг.
4. Субъект, предоставляющий деньги в долг есть:
а) кредитор;
б) заемщик;
в) налогоплательщик.
5. Процентная ставка представляет собой:
а) коэффициент наращения;
б) инструмент наращения долга;
в) величину ссуды с последующей выплатой процентов;
г) отношение суммы процентных денег, выплачиваемых за определенный отрезок времени к величине ссуды.
6. Процентная ставка измеряется:
а) сотыми долями ссуды;
б) периодической дробью;
в) в процентах и в виде десятичной дроби.
7. Наиболее часто проценты начисляются:
а) выборочно;
б) дискретно;
в) непрерывно.
8. Наращением или ростом первоначальной суммы называют:
а) рост процентной ставки за последующие периоды начисления процентов;
б) увеличение денег в связи с присоединением процентов к сумме долга;
в) различные виды процентных ставок.
9. В количественном финансовом анализе процентная ставка является:
а) показателем степени доходности финансовой операции;
б) инструментом способа начисления процентов;
в) коэффициентом, определяющим степень конечной суммы долга.
10. Простыми процентами называются проценты:
а) начисляемые периодически в течение всего срока ссуды;
б) часть начальной суммы долга;
в) начисляемые на одну и ту же начальную сумму.
11. Сложными процентами называются проценты, которые начисляются:
а) один раз в год;
б) ежеквартально;
в) на сумму с начисленными на нее процентами в предыдущем периоде;
г) в течение всего срока ссуды.
12. «Плавающие» процентные ставки означают:
а) переменные ставки;
б) сложные процентные ставки;
в) добавки к базовой величине процентной ставки.
13. Наращенная сумма ссуды есть:
а) первоначальная ее сумма вместе с начисленными на нее процентами;
б) сумма долга, выплаченная раньше обозначенного срока;
в) изменение суммы долга по сложным процентам.
14. Формула наращения по простым процентам:
а) P(1-n/i); б) P(1+n/i); в) P(i+ni); г) P/(1+ni).
15. Наращенная сумма всегда:
а) больше первоначальной суммы;
б) меньше первоначальной суммы;
в) равна первоначальной сумме.
16. При первоначальной сумме ссуды 10000 руб. и процентной ставке простых процентов 12 % годовых наращенная сумма через два года составит:
а) 13000 руб.;
б) 12600 руб.;
в) 12400 руб.
17. Коэффициент наращения при процентной ставке простых процентов 10% годовых за три года составит:
а) 1,25 б) 2,15 в) 1,5 г) 1,3
18. Обыкновенный (коммерческий) процент получают, когда за базу сравнения берут:
а) действительное число дней в году (К = 365)
б) число дней в году (К=360)
с) непрерывное начисление процентов.
19. Наращенная сумма за 100 дней при процентной ставке простых процентов 7% первоначальной сумме 50000 руб. и при точном проценте составит:
а) 50959 руб. б) 51125 руб. в) 50324 руб.
20. Формула наращенной суммы при простых переменных процентных ставках:
а) S(1 - ∑ nkik); б) Р(1+кn); в) Р(1 + ∑ nkik).
21. Множитель наращения за 1 год при ставках простых процентов за 1-ое полугодие – 12% годовых и за 2-ое полугодие – 10% годовых составит:
а) 1,25; б) 1,11; в) 1,17
22. Реинвестирование есть процесс, когда:
а) сумма долга погашается частями;
б) сумма депозита увеличивается в несколько раз;
в) сумма с процентами опять инвестируется.
23. При трехкратном реинвестировании через каждый год первоначальная сумма в 15000 руб. за 3 года при простой процентной ставке 8% годовых возрастает до величины:
а) 17398 руб.; б) 20157 руб.; в) 18896 руб.
24. Дисконтирование есть:
а) определение суммы долга на любой последующий момент времени;
б) операция наращения начальной суммы долга;
в) задача, обратная наращению процентов.
25. Величину начальной суммы долга, найденную дисконтированием, называют:
а) приведением;
б) коммерческим учетом;
в) современной величиной конечной суммы долга.
26. При математическом учете для определения текущей стоимости используется соотношение:
а) а) Р= S(1+ni); б) Р= S /(1+ni); в) Р= S + кn.
27. Для расчета процентов при коммерческом учете используется:
а) ставка наращения;
б) учетная ставка;
в) скидка с конечной суммы;
г) переменная ставка процентов.
28. Для указанной в векселе суммы 20000 руб. при сроке ссуды 1,5 года и учетной ставке 7% годовых фактически полученная заемщиком сумма составляет:
а) 18200 руб.; б) 17100 руб.; в) 17900 руб.
29. Заемщику выплачена сумма 10200 руб. при указанной сумме долга в векселе 15000 руб. Ссуда выдана сроком на 2 года. Такие условия соответствуют учетной ставке:
а) 16% б) 12% в) 9%
30. Ссуда выдана на 120 дней по простой учетной ставке 7% годовых. Заемщик получил 18100 руб. Какая сумма долга проставлена в векселе при таких условиях. Временная база составляет 360 дней.
а) 19627 руб. б) 18532 руб. в) 18800 руб.
Тест 2
1. Платежное обязательство составлено на 100 дней, где указана сумма ссуды 1 млн. рублей. Сумма выдана под учетную ставку простых процентов 12 % годовых. Сумма полученная заемщиком составляет (при К = 360 дней):
а) 1010125 руб.; б) 925102 руб.; в) 966667 руб.
2. При простой ставке наращения 10 %, начальной сумме долга 12000 руб., конечной сумме долга 15000 руб. продолжительность ссуды (в годах) составляет:
а) 1,5 года; б) 2,0 года; в) 2,75 года; г) 2,5 года.
3. Уровень процентов ставки может служить:
а) критерием эффективности финансовой операции;
б) альтернативой выбранной схемы расчета;
в) процентными деньгами.
4. Маржа во внешнеэкономических операциях является:
а) исходной суммой долгового обязательства;
б) надбавкой к базовой величине процентной ставки;
в) изменяющейся во времени базовой величины ставки процентов.
5. Уровень простой процентной ставки можно определить по формуле:
а)
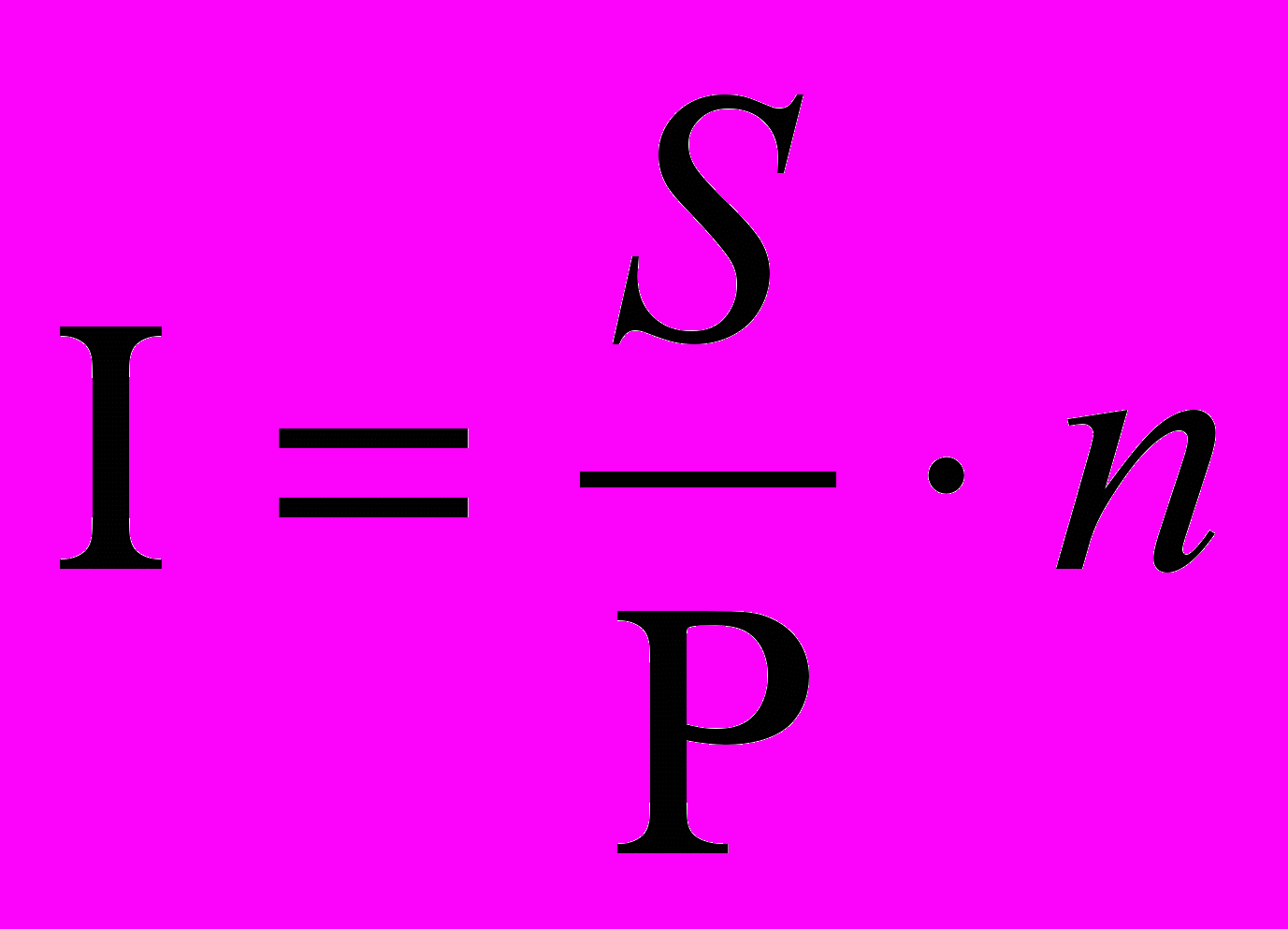; б) I=(S-P)∙P∙H; в) I=(S-P)/P∙n.6. Наращение по простым процентам для кредитора выгодно при продолжительности срока ссуды n:
а) 2 года; б) 1,5 года; в) меньше одного года.
7. Присоединение начисленных процентов к сумме, которая являлась базой для их начисления, называют:
а) дисконтированием;
б) наращивание по сложным процентам;
в) капитализацией процентов.
8. Формула наращения по сложным процентам:
а) S=P(1-in); б) S=P(1+in); в) S=P/(1-in); г) S=P(1+i)n
9. Срок ссуды составляет три года. Первоначальная сумма равна 10000 руб. Сложная процентная ставка наращения составляет 12 % за первый год, 10 % - за 2-й и 3-й год. Наращенная сумма через 3 года составит:
а) 13552 руб.; б) 14227 руб.; в) 12936 руб.
10. Через сколько лет удвоится сумма при ставке простых процентов 6 % годовых:
а) 6,5 года; б) 16,7 года; в) 12,3 года.
11. Сколько лет необходимо ждать (приближенно) пока сумма удвоится по ставке сложных процентов 6% годовых:
а) 7,3 года; б) 13,52 года; в) 11,67 года.
12. При расчете смешанным методом наращенная сумма за 2,5 года при ставке сложных процентов 8% годовых и первоначальной сумме 13000 рублей составляет:
а) 15570 руб.; б) 16335 руб.; в) 15120 руб.
13. Номинальная годовая процентная ставка применяется в случае, когда:
а) число периодов начисления в году – m раз;
б) ставки процентов изменяются в отдельные периоды времени;
в) периоды начисления процентов имеют различную продолжительность.
14. Число периодов начисления при m-разовом начислении в году за n лет составляет:
а) N=m/n; б) N=m∙n; в) N=m+n.
15. Какой эффективной ставке процентов соответствует номинальная ставка процентов 12% при поквартальном начислении процентов:
а) Iэ=13,43%; б) Iэ=11,51%; в) Iэ=12,55%.
16. Какую сумму получит заемщик при сложной учетной ставке 9% годовых, если в векселе указана сумма ссуды 20000 руб. при сроке ссуды 2 года:
а) 16230 руб.; б) 16562 руб.; в) 17200 руб.
17. Дисконт при сложной учетной ставке 8% годовых за 3 года ссуды при сумме, указанной в долговом обязательстве в размере 30000 руб. составляет:
а) 6639 руб.; б) 5823 руб.; в) 6200 руб.
18. Какой номинальной ставке процентов соответствует эффективная ставка 10% при начислении процентов по полугодиям:
а) 10,2%; б) 9,76%; в) 9,35%.
19. При математическом учете по сложным процентам текущая стоимость суммы ссуды определяется как:
а) P=S(1+i)-n б) P=S(1+i)n в) P=S/(1+ni)
20. какую сумму следует указать в долговом обязательстве, если реально выданная сумма составляет 25000 рублей, срок погашения – 3 года, а вексель рассчитан по сложной годовой учетной ставке 10%.
а) 24900 руб. б) 3567 руб. в) 34293 руб.