Науково-методичне забезпечення модернізації системи освіти. Методичний вісник №46. Кіровоград: 2010. 296 с
| Вид материала | Диплом |
- О. В. модель науково-методичного забезпечення якості освіти сільського регіону Методичні, 190.91kb.
- План Що включає науково-методичне забезпечення навчального процесу? Законодавчо-правова, 442.07kb.
- Науково-методичного забезпечення, 1369.35kb.
- Бахін В. П. Тактика допиту. К., 1997., 1212.4kb.
- Науково-методичний центр вищої освіти, 579.99kb.
- Суть І перспективи, 44.33kb.
- Методична робота, 219.51kb.
- Кредитно-модульная система обучения, 74.26kb.
- Облеми «Створення умов для якісної освіти за рахунок сучасного науково-методичного, 512.89kb.
- Атеріали науково-методичне забезпечення викладання економічних дисциплін за умов Болонського, 669.7kb.
Результативність участі учнів закладів освіти області
в ІІІ етапі Всеукраїнських олімпіад
| Роки | Класи | Всього учасників | Отримано дипломів | Райони, які не брали участі в олімпіаді | ||||||
| I | II | III | ||||||||
| 7 | 8 | 9 | 10 | 11 | ||||||
| 2004 | 7 | 10 | 11 | 13 | 15 | 56 | 4 | 9 | 13 | Вільшанський, Петрівський, Ульяновський, Устинівський, Новоархангельський, Онуфріївський, м.Знам′янка |
| 2005 | 12 | 16 | 13 | 15 | 19 | 75 | 3 | 6 | 12 | Вільшанський, Гайворонський, Ульяновський, Устинівський, Компаніївський, Новоархангельський |
| 2006 | 9 | 15 | 17 | 15 | 22 | 78 | 5 | 10 | 10 | Вільшанський, Світловодський, Ульяновський, Устинівський, Новоархангельський |
| 2007 | 12 | 12 | 16 | 22 | 17 | 79 | 5 | 8 | 10 | Знам’янський, Світловодський, Онуфріївський, Олександрійський, Новомиргородський |
| 2008 | 33 | 17 | 20 | 29 | 29 | 128 | 5 | 10 | 13 | Вільшанський |
| 2009 | 25 | 28 | 20 | 29 | 23 | 125 | 5 | 9 | 10 | Вільшанський, Онуфріївський |
| 2010 | 20 | 22 | 16 | 22 | 22 | 102 | 5 | 10 | 15 | Вільшанський, Онуфріївський, Ульяновський, Устинівський, Новгородківський, Голованівський, Олександрівський |
З наведених даних можна зробити висновок про те, що у районах, учні яких систематично не беруть участі в олімпіадах, не приділяють належної уваги щодо виявлення обдарованих і талановитих дітей та підготовки їх до математичних змагань.
Найбільш масовими конкурсами з математики є Міжнародний математичний конкурс «Кенгуру» для учнів 2-11 класів та заочний конкурс «Золотий ключик». На виконання наказів МОН України «Про участь школярів України у Міжнародному математичному конкурсі «Кенгуру» від 24.05.2000 р. №149 та «Про проведення заочного математичного конкурсу «Золотий ключик» для учнів 4-9 класів навчальних закладів щодо популяризації математичних знань серед учнівської молоді, розвитку здібностей і логічного мислення широкого кола учнів, активізації творчої діяльності вчителів, а також пошуку і підтримки обдарованих дітей» учні області щорічно беруть участь у даних змаганнях, які з кожним роком набувають все більшої популярності.
Динаміка зростання кількісного складу учасників Міжнародного математичного конкурсу «Кенгуру»
| Рік | 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 | 2008 | 2009 |
| К-сть учасників | 15 | 28 | 46 | 98 | 195 | 364 | 671 | 1188 | 3323 | 5891 | 7490 |
Найбільше учасників цього конкурсу у Гайворонському, Добровеличківському, Маловисківському районах, м.Кіровограді та м.Олександрії. Найменша кількість – в Устинівському, Новомиргородському, Новгородківському та Долинському районах. За результатами конкурсу відповідно до квоти кілька років поспіль учні області мали змогу оздоровитись в літньому таборі, що знаходиться у Лівадії поблизу Ялти.
Головною привабливістю конкурсу «Золотий ключик» є його завдання. Вони різноманітні за рівнем та змістом. Більшість з них не вимагають спеціальної підготовки, а розраховані на винахідливість та ініціативу при їх розв’язанні. Вони сприяють розвитку логічного і образного мислення, формуванню вмінь застосовувати математичні знання.
Склад учасників конкурсу за віковими групами (заочний тур)
| Класи | 4 | 5 | 6 | 7 | 8 | 9 | Всього | |
| Кількість учнів | 2007 рік | 4 | 20 | 7 | 5 | 6 | 7 | 49 |
| 2008 рік | 10 | 12 | 15 | 14 | 4 | 1 | 56 | |
| 2009 рік | 12 | 13 | 15 | 15 | 5 | 2 | 62 | |
Особливої подяки заслуговують вчителі Добровеличківського, Петрівського районів та м.Олександрії (Поважнюк І.В., Глущенко Л.І., Носова С.І.), чиї учні є активними учасниками «Золотого ключика».
Участь у даних конкурсах допомагає вчителям у формуванні в учнів інтересу до предмета, у заохоченні до занять математики, а для учнів - це є підказка, як знайти баланс у процесі використання традиційних та новітніх джерел інформації.
Ефективність впровадження профільного навчання залежить не лише від організації, готовності вчителів до змін та керівників шкіл забезпечити ці зміни, а й від фінансування даного процесу. За відсутності однієї з умов реалізація Концепції профільного навчання неможлива, потрібні спільні зусилля зацікавлених структур.
Л.А.Ткаченко,
завідувач навчально-методичного кабінету математики
Сільський учитель і сучасність:особистісний вимір
В українській освіті, як і в суспільстві в цілому, за роки незалежності сталися значні зміни. Кожна людина має орієнтуватись у громадсько-політичній та економічній ситуації сім’ї, підприємства або території проживання, а незабаром й існувати, вміючи користуватись інформаційними технологіями, бути носієм інформаційної культури, яка вже зараз стає атрибутивною частиною загальної культури. Сьогодні без комп’ютера неможливо обійтись в будь-якій діяльності людини. Удосконалення навчального процесу через впровадження комп’ютерних технологій перебуває у прямій залежності від того, наскільки воно побудовано на науковій основі, як вчитель сприйме й застосує досягнення науки і техніки, нових форм роботи. Продуктивність і якість праці вчителя багато в чому залежить від оперативного інформування, тобто своєчасного отримання та опрацювання необхідної інформації. Використання алгоритмів, таблиць, схем упорядковує процес навчання. У зв’язку з гострою проблемою заощадження часу у навчальному процесі перед сучасною школою стоїть завдання – знайти засоби і прийоми навчання, що дозволяють максимально економити час на уроці, підвищити рівень сприйняття і розуміння учнями матеріалу. В.О.Шарандак впевнена, що однією з можливостей підсилити мотивацію навчальної діяльності учнів є використання в процесі навчання інформаційно-комунікативних технологій
Шарандак Олена Василівна,
вчитель математики вищої категорії, старший вчитель Вільхівської загальноосвітньої школи І – ІІІ ступенів імені Л.В.Куценка Ульяновського району.
- Закінчила Уманський педагогічний інститут ім. П. Тичини.
- Педагогічний стаж – 35 років.
- Працює над реалізацією принципів особистісно орієнтованого навчання, використовує інтерактивні методи, впроваджує новітні освітні технології у навчально-виховний процес.
- Керує районним методичним об’єднанням учителів математики.
- Лауреат обласного конкурсу «Учитель року – 2004».
- Бере активну участь в обласних та районних семінарах, тренінгах з впровадження інформаційних технологій у навчально-виховний процес.
- Її учні є призерами й переможцями районних і обласних конкурсів, олімпіад.
- Багато років веде заняття шкільного гуртка «Юний математик».
- Нагороджена грамотами Ульяновського районного відділу освіти, Кіровоградського обласного управління освіти і науки, Міністерства освіти і науки України; нагрудним знаком «Відмінник освіти України».
Нині якісне викладання дисциплін не може здійснюватися без використання засобів і можливостей, які надають комп’ютерні технології. Адже вони допомагають вчителю доступніше подати матеріал, зробити його цікавим, швидко перевірити знання учнів та підвищити їх інтерес до навчання. Новітні підходи до організації навчання роблять навчально-виховний процес різноманітним, цікавим та ефективним.
Залучення комп'ютерних технологій на різних етапах навчання допомагає О.В.Шарандак реалізувати основний принцип особистісно орієнтованого підходу в освіті – принцип діяльності. Сутність цього принципу полягає в стимуляції учнів до освітньої діяльності, що забезпечує можливості саморозвитку, самовираження і самоосвіти.
Комплексне використання різних засобів навчання сприяє створенню сприятливого пізнавального середовища. Олена Василівна, поєднуючи традиційні форми і види роботи на уроці з комп’ютерною підтримкою, максимально диференціює та індивідуалізує навчання, робить процес навчання творчим, дослідницьким. Застосування інформаційних технологій дає змогу скоротити час на вивчення теми, підвищити рівень сприйняття і розуміння учнями матеріалу. Позитивний результат гарантовано, бо молодь до комп’ютерів ставиться доброзичливо, вона їх любить, їм довіряє, навіть їх обожнює. Вчитель розумно використовує це ставлення школярів до комп’ютера при плануванні навчального процесу.
Учні мають різний психологічний статус, і багато хто з них хворобливо ставиться до зауважень, боїться зазнати фіаско на очах у класу. У діалозі з комп'ютером нічого подібного не відбувається: комп'ютер не рахує, скільки було невдалих спроб розв’язання задачі, не робить ніяких зауважень. Він ще й підкаже, що і як потрібно зробити. Враховуючи психологічні аспекти, О.В.Шарандак формує ситуацію психологічного комфорту, яка створює можливість пізнавального та емоційного розкріпачення учнів. Саме це уможливило використання персонального комп’ютера для навчання і виховання підростаючого покоління.
Особливе місце у підтримці уроку математики займає педагогічне програмне забезпечення, яке підтримує і теоретичну, і практичну частини курсу математики, дає можливість моделювати хід розв’язування математичної задачі.
Для комп’ютерної підтримки проведення уроків з математики в старших класах Олена Василівна використовує ППЗ GRAN-1, GRAN-2D, GRAN-3D . Це дає можливість доступніше викладати ряд тем курсу математики:
побудова графіків функцій, розв’язування систем рівнянь і нерівностей, знаходження площ фігур, обмежених графіками функцій, об’ємів тіл обертання. Виклад нового матеріалу за допомогою комп’ютерного програмного забезпечення більш наочний, доступний, образний, насичений, динамічний і результативний. Олена Василівна використовує ППЗ для:
демонстрації нових понять, фактів;
відпрацьовування алгоритмів розв’язання різних задач;
тренінгу, що вимагає нових знань і набуття умінь;
самоперевірки засвоєння понять, знань;
контролю (перевірки) якості засвоєння знань і набутих навичок;
творчої навчальної діяльності учнів.
Вивчення теми «Застосування похідної. Дотична до графіка функції» (11 клас) потребує від учнів усвідомленого розуміння геометричного змісту похідної, високої графічної культури і розвинутих обчислювальних навичок. Алгоритм знаходження рівняння дотичної до графіка функції в заданій точці легко запам'ятовується учнями. Але через необхідність значних витрат часу для побудови графіка функції і дотичної до нього в заданій точці учні найчастіше виконують подібні завдання формально (за зразком). При цьому вони можуть не розуміти, як проаналізувати властивості функції, якщо відоме рівняння дотичної в даній точці. В такій ситуації вчителька пропонує практичну роботу з комп'ютерною підтримкою, що сприяє розвитку свідомого застосування похідної до знаходження дотичних, до графіка заданої функції, допомагає засвоїти геометричний і механічний зміст похідної, його застосування до дослідження властивостей функції. Учні мають можливість побачити на екрані монітора графік функції і побудовану дотичну по знайденому ними рівнянню; порівнюють результати своєї роботи з еталоном; одержують оцінку за якість засвоєння навчального матеріалу.
Із задоволенням виконують учні контрольну роботу, що складена у формі тестів, провести і перевірити яку допомагає персональний комп’ютер. Учні вводять отриманий результат у комп’ютер. І у разі успіху, і у разі помилки комп’ютер відразу повідомляє правильну відповідь. Таким чином школяр має можливість проаналізувати свої помилки. Під час виконання роботи можна робити деякі записи, а якщо це контрольна робота з геометрії, то необхідним є виконання малюнків. Даний підхід до використання комп'ютерних технологій відкриває широкі можливості в забезпеченні своєчасної перевірки й обліку навчальних досягнень учнів, а учень стає суб'єктом пізнавальної діяльності. З іншого боку, вчитель своєчасно перевіряє й обліковує навчальні досягнення учнів. Отже, підвищується зацікавленість школярів у пізнавальній діяльності, формується їх свідоме ставлення до навчання, адекватна самооцінка, збільшується щільність навчальної діяльності
Особливо, вважає Олена Василівна, доцільно використовувати комп’ютери для проведення тестування з різних тем математики, що дає змогу швидко оцінити навчальні досягнення учнів, охопивши одночасно весь клас, забезпечити можливість працювати індивідуально. Тестування як засіб педагогічної діагностики дозволяє оперативно і точно визначити рівень знань окремого учня. Систематична робота з комп’ютерним тестом повинна стати для учня звичною справою тоді зростуть його шанси на успішне складання незалежного зовнішнього тестування. Широке використання тестової перевірки знань при вивченні математики підвищує ефективність навчально-виховного процесу через створення атмосфери довіри, відкритості, об’єктивності, забезпечує оперативний зворотний зв’язок, дозволяє проводити миттєвий аналіз та корекцію процесу навчання.
Контрольно-діагностична система TEST-W призначена для перевірки знань тестуванням на комп'ютері і є хорошим програмним середовищем для створення тестів з математики.
У процесі використання комп’ютера в навчальному процесі вирішуються наступні психолого-педагогічні проблеми:
- комп’ютер підвищує активність роботи учня, збуджує інтерес до навчання;
- індивідуальна робота з комп’ютером сприяє розвитку самостійності;
- спілкування з комп’ютером привчає до точності, акуратності, послідовності дій;
- робота з комп’ютером сприяє розвитку здатності до аналізу й узагальнення;
- комп’ютер полегшує засвоєння абстракцій, дозволяє представити їх конкретними.
Широке впровадження в навчальний процес нових інформаційних технологій навчання, що базуються на комп’ютерній підтримці навчально-пізнавальної діяльності, відкриває перспективи щодо гуманізації навчального процесу, розширення та поглиблення теоретичної бази знань і надання результатам навчання практичної значущості, інтеграції навчальних предметів і диференціації навчання відповідно до запитів, нахилів та здібностей учнів, інтенсифікації навчального процесу й активізації навчально-пізнавальної діяльності, посилення спілкування учнів і вчителя та учнів між собою, збільшення питомої ваги самостійної навчальної діяльності дослідницького характеру, розкриття творчого потенціалу учнів і вчителів з урахуванням їхніх позицій та вподобань, специфіки перебігу навчального процесу.
Крім звичайної мети, урок з комп’ютерною підтримкою має технологічну мету. Головна особливість – перевизначення потоків інформації на уроці, діалог вчителя з учнем відбувається через комп’ютер, який виступає в ролі третього компонента навчання, індивідуального для кожного учня.
Можна виділити три основні задачі, які необхідно розв’язати для успішного проведення комп’ютеризованого уроку: дидактичну, методичну та організаційну. Під дидактичним забезпеченням розуміють навчальні матеріали уроку. Методична задача – визначення методів використання комп’ютерів при викладанні теми, аналіз результатів уроку і постановка наступної навчальної мети. Організаційна задача, яка легко вирішується під час традиційного уроку, стає головною. Вона полягає в тому, щоб виробити і закріпити в учнів навички роботи з навчальною програмою, організувати роботу, уникаючи перевантаження та нераціональне використання часу.
Залучення комп’ютера до навчально-виховного процесу – це залучення не тільки техніки, а й того зовнішнього інтелекту, який презентовано через технологію та програмне забезпечення. Таким чином, застосування комп’ютера в навчально-виховному процесі за умови правильного визначення його місця дає підстави сподіватися на певні зрушення, поворот дидактичного простору обличчям до майбутнього, яке проектується сьогодні.
При викладанні теми «Чотирикутники» Олена Василівна використовує педагогічний програмний засіб «Бібліотека електронних наочностей «Геометрія, 7 – 9 класи» для ЗНЗ».
Наприклад, розкриваючи тему «Ромб, квадрат та їх властивості» формує поняття ромба, квадрата та їх властивостей; доводить властивості діагоналей ромба; узагальнює властивості чотирикутників; розвиває вміння виділяти головне, порівнювати; розвиває в учнів інтерес до вивчення математики, до роботи з комп’ютерною технікою; виховує самостійність. Етап уроку Повторення і систематизація теоретичних відомостей з теми «Чотирикутники» О.В.Шарандак планує таким чином.
Теоретична розминка
На комп’ютерах учитель набирає запитання з теми «Чотирикутники» у Microsoft Office Word. Учні відповідають одним словом («так» чи «ні»).
Запитання
Якщо протилежні сторони чотирикутника рівні, то він паралелограм?
- Діагоналі прямокутника рівні?
- У паралелограма всі сторони рівні?
- Діагоналі паралелограма рівні?
- У паралелограма діагоналі взаємно перпендикулярні?
- У прямокутника всі сторони рівні?
- У паралелограма всі кути рівні?
- У чотирикутника можна провести чотири діагоналі?
- У паралелограма і прямокутника всі властивості однакові?
- У прямокутника протилежні кути рівні?
(Правильність виконання даного завдання учитель перевіряє за своїм комп’ютером, а якщо не підключена мережа, то результати заносить до наперед заготовленої таблиці).
Мозковий штурм
(Усне розв’язання задач за готовими малюнками)
1. В С

50°
А D
ВС ║АD, АВ║СD
< В-?, <С-?, < D-?
2. М 25 см К

13см
А Р - ? С
Новий матеріал діти опрацьовують самостійно, використовуючи ППЗ «Геометрія. 7 – 9 класи» за алгоритмом:
Відкриваємо дану програму. У змістові знаходимо розділ «Чотирикутники», де вибираємо тему «Ромб». Починаємо вивчення теми, клацнувши мишкою на команді Перегляд. На екранах монітора висвітлюється малюнок ромба, його елементи, дається означення. Для зміни форми ромба учні зафіксовують курсором миші будь-яку вершину та пересувають її. Роблять висновок.
Потім розглядають рухомий малюнок, де показано, що:
- діагоналі перпендикулярні і точкою перетину діляться пополам;
- обидві діагоналі є бісектрисами всіх внутрішніх куті;
- прямі, що містять діагоналі, є осями ромба.
Розглядають доведення теореми. Діагоналі ромба перетинаються під прямим кутом. Діагоналі ромба є бісектрисами його кутів.
Учні встановлюють зв'язок між прямокутником і ромбом:
- якщо з’єднати відрізками середини сусідніх сторін довільного прямокутника, то отримаємо ромб;
- якщо з’єднати відрізками середини сусідніх сторін довільного ромба, то отримаємо прямокутник.
Потім учні опрацьовують тему «Квадрат».
На екранах монітора висвітлюється малюнок квадрата, його елементів, дається означення. Для зміни форми квадрата, учні зафіксовують курсором миші будь-яку вершину та пересувають її. Роблять висновок.
Розглядають рухомий малюнок, де показано, що:
- діагоналі квадрата рівні, перпендикулярні і точкою перетину діляться навпіл;
- квадрат має чотири осі симетрії:
- прямі, що проходять через середини протилежних сторін;
- прямі, що містять діагоналі.
• Квадрат переходить сам у себе при повороті на 90°.
Етап уроку «Закріплення й осмислення нового матеріалу»
Після опрацювання теоретичного матеріалу учні заповнюють таблиці.
| Властивості ромба | Властивості квадрата | Спільні властивості |
| | | |
Складають діаграму Вена.
Заповнюють таблицю, ставлячи знак «+», якщо чотирикутник має відповідну властивість, і «-», якщо ні.
| Вид чотирикутника Властивості | паралелограм | прямокутник | ромб | квадрат | трапеція |
| Протилежні сторони попарно паралельні | | | | | |
| Всі кути рівні | | | | | |
| Всі сторони рівні | | | | | |
| Діагональ поділяє на два рівних трикутники | | | | | |
| Протилежні сторони і кути рівні | | | | | |
| Діагоналі рівні | | | | | |
| Діагоналі є бісектрисами кутів | | | | | |
| Діагоналі взаємно перпендикулярні | | | | | |
| Сума кутів, прилеглих до однієї сторони, дорівнює 180° | | | | | |
| Діагоналі в точці перетину діляться пополам | | | | | |
При вивченні у 10 класі розділу «Тригонометричні функції» за допомогою програмного забезпечення для підтримки навчання алгебри в школі, Олена Василівна вчить будувати графіки тригонометричних функцій
y = sin x, y = cos x; формувати уміння будувати графіки: y =A sin(kx+b),
та y = A cos (kx+b), виховує культуру побудови графіків.
Перевірка домашнього завдання здійснюється у вигляді тестів, які складаються у Microsoft Office Excel.
Запитання для тестів.
- Визначити, кутом якої чверті є кут 390°:
А) І чв.; Б) ІІ чв.; В) ІІІ чв.; Г) ІV чв.
- Відношення ординати точки кола до його радіуса називається:
А) косинусом; Б) тангенсом; В) синусом; Г) котангенсом
- Синус (-270°) дорівнює:
А) 0; Б) 1; В) -1; Г) не існує
- Який знак має tg (-70°):
А) « +»; Б) «-» ; В) не існує; Г) не має відповіді
- Знайти значення sin £, якщо Sin (£ +2π) = 0,5:
А) 0; Б) -1; В) 0,5; Г) 1
- Період синуса дорівнює:
А) π; Б) 2π; В) π+2; Г) π/2
- Область визначення функції позначається:
А) Е; Б) D; В) F; Г) Т
Повторення і систематизація теоретичних відомостей з теми «Тригонометричні функції».
Запитання до класу.
- Сформулюйте означення функції. Наведіть приклади.
- Якими способами можна задати функцію? Навести приклади.
- Що називається графіком функції?
- Що називається областю визначення та множиною значень функції?
- Яка функція називається парною? Непарною?
- Дати означення спадної функції; зростаючої функції.
- Дати означення синуса, косинуса, тангенса та котангенса числа α.
- Назвати одиниці вимірювання кутів.
- Дати означення радіана.
- Який зв'язок між радіанною та градусною мірою?
- Яке коло називається одиничним?
- Дати означення періодичної функції.
- Назвати періоди тригонометричних функцій.
При вивченні нового матеріалу для побудови графіків даних функцій вчитель використовує програмне забезпечення CRAN 1.
Щоб побудувати графік функції y = sin x:
- Відкриваємо ППЗ «ALGEBRA» → CRAN_W → CRAN 1.
- Вибираємо «Об’єкт» → «Створити» – у діалоговому вікні «Введення функції» вводимо функцію y = sin x, Ok., потім вибираємо «Побудувати графік» і в полі зображення буде відображено графік даної функції.
За графіком даної функції колективно пояснюють його побудову. Роблять висновок . Графіком функції y = sin x є синусоїда. Далі покроково будують графік функції виду y = A sin (kx+b), роблять висновок.
Графік функції y = A sin (kx+b) утворюється за допомогою такої послідовності перетворень:
- стисканням графіка функції y = sin x у k раз вздовж осі абсцис дістаємо графік функції y = sin kx;
- перенесенням графіка функції y = sin kx на (b; 0) дістанемо графік функції y = sin(kx+b);
- розтяганням графіка y = sin(kx+b) у А раз вздовж осі ординат дістаємо графік функції.
Для кращого сприйняття зображення графіка є колірна відповідність текстової та графічної інформації: колір тексту формули і відповідного графіка функції той самий. Графіком цієї функції є також синусоїда. Отже, роблять висновок: синусоїдою називають не тільки графік синуса, а й будь-яку криву, утворену з нього стисканням (розтягуванням) вздовж осей і наступних рухів або перетворень подібностей.
За аналогічною схемою будуються графіки функцій y = cos x;
y =A cos (kx+b), робляться відповідні висновки.
Закріплення й осмислення нового матеріалу вчитель проводить у вигляді самостійної роботи.
Побудувати графіки функцій:
y = sin(x - π /6); y = cos (x/2); y = 2sinx -1;
y =1/2 (cos x); y = 3sin(0,5x+1); y = -2cos(2x+1).
Велике значення має використання комп’ютерів в позаурочний час для проведення конкурсів, змагань. Особливо учні люблять працювати за комп’ютерами на заняттях шкільного гуртка «Юний математик», який веде Олена Василівна. Вони складають та розгадують кросворди; проводять змагання з малювання, використовуючи різні геометричні фігури у програмі «Paint».
Приклади застосування комп’ютерів на заняттях математичного гуртка
Складання кросвордів в Microsoft Excel.
Для того, щоб скласти кросворд в Microsoft Excel потрібно виділити аркуш і розділити на клітинки: Формат → рядок → висота записуємо число(10; …)
знову Формат → стовпець → ширина записуємо число (1; ...)
Креслимо кросворд: виділяємо кількість клітинок для першого слова Формат→ клітинки→ межа → зовнішні(ширина лінії) → внутрішні, Ок.
Нумеруємо клітинки 1, 2, 3…, підводимо мишку на цифру 1 і клацаємо правою кнопкою, вибираємо команду додати примітку і записуємо перше запитання. Далі виділяємо клітинки першого слова, вибираємо Формат→ умовне форматування з'являється діалогове вікно Умовне форматування, де у першому віконці вибираємо значення, у другому дорівнює, а в третьому записуємо першу букву слова-відповіді.
Аналогічно заповнюємо весь кросворд.
Кросворд можна форматувати на свій смак, використовуючи різні шрифти, кольори шрифтів, заливку і т.д.
Конкурс «художників» у програмі «Paint».
Використовуючи різні геометричні фігури, учні малюють людину, квітку, тваринку і т.д.

Розв’язування задач у Microsoft Excel складанням загальної формули.
Обчислити периметр та площу трикутників за такими даними:
| | A | B | C | D | E |
| 1 | a | b | c | p | s |
| 2 | 3 | 4 | 5 | | |
| 3 | 10 | 13 | 17 | | |
| 4 | 21,4 | 35,7 | 41,9 | | |
| | * * * | * * * | * * * | | |
Для того, щоб виконати обчислення, учні повинні знати формули для знаходження периметра трикутника та площі трикутника за відомими сторонами. У клітинці D2 записується формула для знаходження периметра трикутника: =(A2+B2+C2)/2. Ця формула справедлива для всіх даних цієї таблиці. Тому виділяємо цю клітинку і підводимо вказівник миші до її правого нижнього кута. Вказівник має форму хрестика. Натиснувши і втримуючи ліву клавішу миші, потягнемо маркер заповнення вниз до останньої клітинки створюваної таблиці. У всіх клітинках стовпчика D з’являться певні значення. Якщо виділити будь-яку клітинку цього стовпчика, то в рядку формул побачимо формулу, записану в цій клітинці. В клітинці E2 аналогічно записуємо формулу для знаходження площі трикутника (формула Герона) =SQRT(D2*(D2-A2)*(D2-B2)*(D2-C2)).
Побудова діаграм у Microsoft Excel
Діаграма – це малюнок, на якому можна наочно відобразити, як змінюється деяка величина залежно від певних факторів.
Для того, щоб створити діаграму, необхідно спочатку ввести для неї дані на аркуші електронної таблиці. Потім ці дані слід виділити й запустити майстер діаграм, який дає можливість у покроковому режимі задати параметри діаграми. Діаграма зв’язана з даними електронної таблиці, на основі якої вона побудована, а коли відбуваються зміни цих даних – вона автоматично оновлюється.
- Складаємо таблицю.
- Виділяємо діапазон клітинок таблиці.
- Вибираємо меню Вставка → Діаграма, відкривається перше вікно майстра діаграм. У списку Тип вибираємо тип діаграми, клацаємо на кнопці Далі. Відкривається друге вікно майстра діаграм, яке містить область попереднього перегляду діаграми, Далі. Відкривається третє вікно майстра діаграм. У полі Назва діаграми вводимо її назву Далі. Відкривається останнє вікно майстра діаграм Готово.
- Діаграму можна редагувати та форматувати.
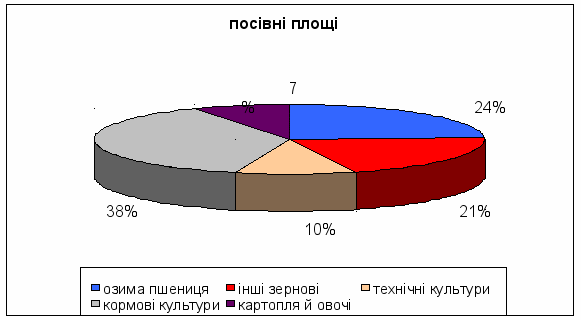
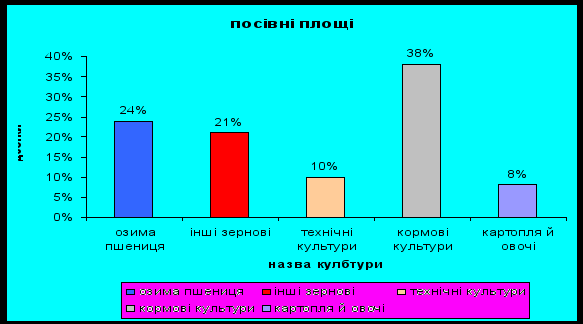
Побудувати діаграму розподілу посівних площ:
-
озима пшениця
24%
інші зернові
21%
технічні культури
10%
кормові культури
38%
картопля й овочі
7%
О.В.Шарандак приділяє увагу роботі з учнями, які вирізняються гарною пам’яттю, мисленням, допитливістю, добре розв’язують задачі, логічно викладають свої думки, мають здібності до практичного застосування знань, тобто з обдарованими дітьми. На кожного з них розроблена картка досягнень.
Картка досягнень обдарованого учня
- Прізвище, ім’я, по батькові
- Дата народження
- Адреса, телефон
- Клас
- Навчальний рік
- Коротка характеристика
- Досягнення
Метою даної роботи є:
- виявлення та сприяння розвитку інтелектуально обдарованих школярів;
- формування готовності до свідомого вибору майбутньої професії, стимулювання школярів до навчання у вищих навчальних закладах;
- сприяння самовираженню учнів у різних видах діяльності; задоволення їх потреб, інтересів та стимулювання творчого самовдосконалення;
- формування покоління майбутніх науковців та практиків, творчих, ініціативних, підприємливих працівників для різних галузей суспільного життя;
- підвищення інтересу до поглибленого вивчення базових дисциплін, виявлення рівня сформованості вмінь дослідницької роботи через гуртки, факультативи, олімпіади;
- виховання компетентної особистості, здатної здійснювати самостійний вибір та приймати відповідальні рішення;
- сприяння вдосконаленню навчально-виховного процесу та застосуванню сучасних прийомів і методів навчання.
Для роботи з кожним учнем складається індивідуальний план роботи.
З метою розвитку в учнів інтересу до вивчення математики, до роботи з комп’ютерною технікою, активності, уваги, наполегливості, логічного мислення та сприяння формуванню інтелектуальних і творчих здібностей Олена Василівна розробила гру «Найрозумніший математик». Вона проводиться у три тури.
І тур (беруть участь 12 учнів).
На 12 комп’ютерах складено по 18 запитань (у вигляді тестів ), на які учні вибирають правильну із чотирьох запропонованих відповідей і набирають відповідну кількість балів, які висвітлюються на моніторі комп’ютера.
Тести складаються у Microsoft Office Excel.
ІІ тур
Шість учнів, які набрали найбільшу кількість балів, стають учасниками ІІ туру.
У другому турі дається 12 категорій знань, і кожний учень по черзі вибирає дві категорії, на які дає відповіді протягом 1 хвилини («Алгебра», «Геометрія», «Математика», «Видатні математики», «Цікаві задачі», «Вислови про математику»,«Планіметрія», «Стереометрія», «Чотирикутники», «Трикутники», «Функції»,«Секрет»)
Для кожної категорії учитель відповідно підбирає по 10-15 запитань.
На шести комп’ютерах учитель набирає запитання для двох категорій у Microsoft Office Word. Учасники відповідають на запитання одним словом: «так» чи «ні».
Наприклад, запитання до категорії «Чотирикутники»
- Термін «паралелограм» був введений Евклідом (так).
- Автором «Начал» є Вієт (ні).
- Слово «ромб» грецького походження (так).
- Дельтоїд не є чотирикутником (ні).
- Чи обов’язково є прямокутником чотирикутник, у якого є прямий кут? (ні)
- Діагоналі чотирикутника перпендикулярні. Чи обов’язково цей чотирикутник – квадрат? (ні)
- Чи являється прямокутником паралелограм, у якого є прямий кут? (так).
- Чи правильно, що будь – який ромб є квадрат? (ні)
- Сума кутів чотирикутника дорівнює 360° (так).
- Площа квадрата із стороною, що дорівнює одиниці вимірювання, дорівнює одиниці (так).
ІІІ тур
Три учні, які набрали найбільшу кількість балів, – учасники ІІІ туру.
Для його проведення потрібно було підготовити тему на вибір, пов’язану із математикою. З кожної теми учасник має відповісти на дев’ять запитань, одержавши при правильній відповіді два бали. Якщо учень дав правильну відповідь із теми суперника, то одержує три бали, а якщо із загальних питань, то одержує один бал. За неправильну відповідь – нуль балів. На одному із комп’ютерів намальовано таблицю. Всі клітинки зафарбовано у чотири кольори. Клітинки білого кольору – це загальні запитання, а три інші кольори відповідають тим темам, які вибрали учасники. Одним кольором зафарбовані запитання однієї теми. На 30 секунд учасникам висвітлюється дана таблиця, вони запам’ятовують свої клітинки. Учасник, який у попередньому турі набрав найбільшу кількість балів, починає гру першим.
Стає переможцем той учасник, який набрав найбільшу кількість балів у третьому турі.
Зразок запитань для третього туру
