Geum.ru

«чувашский государственный педагогический университет им. И. Я. Яковлева»

Вид материалаСборник научно-методических статей

Содержание


К вопросу обучения решению задач
Беляева Зоя Михайловна
Подобный материал:
1   2   3   4   5   6   7   8   9   ...   14
Часть 1

А1. Напишите цифрами число, в котором 15 единиц класса единиц, 520 единиц класса тысяч и четыре единицы класса миллионов.

1. 4520015
2. 4502150
3. 4521500
4. 45215

А2. Из чисел 3817, 3871, 3781, 3718 выберите наибольшее.

1. 3817
2. 3871
3. 3781
4. 3718

А3. Укажите число, в котором число сотен больше числа десятков тысяч.

1. 328700

2. 214000
3. 531202
4. 485800




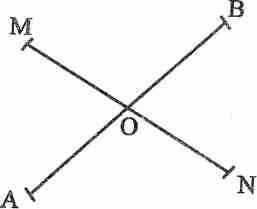
А4. Выберите отрезок, длина которого равна 4 см (рис. 1).

Рис. 1




1. OB
2. AO
3. MO
4. MN

А5. Укажите верное равенство.

1. 92468-80275=993
3. 2529+3456=9785

2. 99900:45=2220
4. 300540=129000

А.6. Вставьте пропущенные цифры и укажите произведение.



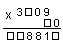
1. 3209
2. 90
3. 28881
4. 288810

А7. Вычислите: 1616125+101244(144-272): (374-122).

1. 20220
2. 101446
3. 202000
4. 20020

А8. Найдите остаток от деления 303111 на 213.

1. 12
2. 22
3. 122
4. 99

А9. На дачном участке посадили 16 рядов роз по 22 куста в ряду и 17 кустов роз посадили отдельно на клумбу. Укажите равенство, которое наиболее точно определяет, сколько кустов роз посадили на участке.

1. 2020+20=420
3. 1020+10=210

2. 2030+10=610
4. 2025+20=520

А10. По рисунку определите число общих точек окружности с прямой АО (рис. 2.



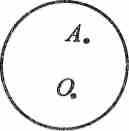
Рис. 2

1. общих точек нет
3. одна общая точка

2. две общие точки
4. три общие точки


Часть 2

В1. Коробка для подарка имеет размеры 40 см, 25 см, 20 см. Сколько сантиметров ленты понадобится, чтобы перевязать коробку, если на узел и концы следует оставить 50 см (рис. 3)?



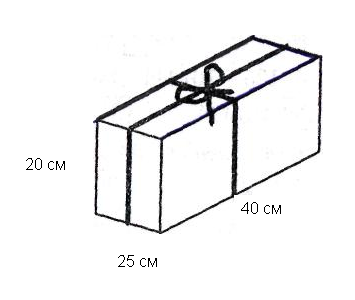
Рис. 3

Ответ: ______

В2. Выразите 987 минут в часах и минутах.

Ответ: ______

В3. Выполните действия: 5370+(17035-5070):35.

Ответ: _______

В4. В двух альбомах находятся марки, причём в первом альбоме в два раза больше марок, чем во втором. В альбомы добавили несколько марок. Пользуясь таблицей, определите, сколько марок добавили в альбомы.

Альбомы
Было

Добавили
Стало

I


II
48 – это в два раза больше, чем во II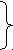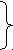

?



?


84

Ответ: ________

В5. Однажды король написал своим друзьям 90 поздравлений на праздник. Он написал 20 писем (рис. 4). Открыток король отправил в два раза больше, чем писем, а остальные поздравления послал электронной почтой. Постройте прямоугольники, которые показывают, сколько король послал открыток и сколько поздравлений по электронной почте.




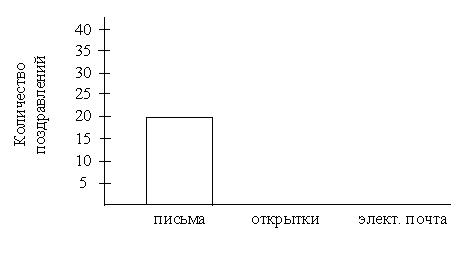
Рис. 4

Часть 3

С1. Найдите закономерность и продолжите последовательность чисел.



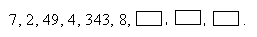
Решение: ___________________________________________________.

Ответ: _______

С2. Бутылка кваса стоит 33 рубля. Квас в бутылке на 29 рублей дороже самой бутылки. Сколько стоит пустая бутылка?

Решение: ___________________________________________________.

Ответ: _______

С3. Петя, Саша и Ваня занимались футболом, а Артём и Денис – хоккеем. Тренер желает выбрать двух футболистов и одного хоккеиста. Сколькими способами это можно сделать?

Решение: ___________________________________________________.

Ответ: _______

Особенностью этих тестов является наличие в них заданий разного уровня сложности. Они охватывают такие разделы, как: «Числа и вычисления», «Геометрические фигуры», «Измерение геометрических величин», «Задачи и процесс ее решения». В заданиях А1-А10 проверяется уровень сформированности представлений о натуральном числе и 0, вычислительных умений и навыков, начальных геометрических представлений. Задания второй и третьей частей рассчитаны на проверку повышенной подготовки учащихся. Они призваны выявить школьников, способных к творческой деятельности, чтобы с ними организовать индивидуальную работу для участия на олимпиадах и различных конкурсах по математике.

Авторы приведенных нами выше тестов [2, 84-89] разработали инструкции для учителей и учащихся по выполнению тестов и условия перевода тестовых баллов в школьные оценки. Все это призвано помочь педагогу в организации промежуточной аттестации младших школьников.


Литература
  1. Глушкова, О. Б. Тесты по математике : учебное пособие для начальной школы / О. Б. Глушкова. – М. : АСТ-ПРЕСС, 1998. – 200 с.
  2. Тесты за курс начальной школы : русский язык, математика, окружающий мир ; под ред. Ф. Ф. Лысенко. – Ростов-на-Дону : Легион, 2008. – 240 с.




Архипова Светлана Емельяновна,
доцент кафедры МНО,
Гайдук Елена,
студентка 5 курса з/о

К ВОПРОСУ ОБУЧЕНИЯ РЕШЕНИЮ ЗАДАЧ

В НАЧАЛЬНЫХ КЛАССАХ

Формирование интереса к учению является важным средством повышения качества обучения школьников. Это особенно важно в начальной школе, когда еще только формируются, а иногда и только определяются постоянные интересы к тому или иному предмету.

Большие возможности для развития интереса учащихся к математике имеют задачи. Понятие «задача» относится к числу широких общенаучных понятий. Любая задача, реально возникающая у человека, зафиксированная в тексте или представленная как-то иначе, содержит в себе некоторую информацию о какой-либо области действительности и требование вывести, получить новую информацию об определенных компонентах той же области действительности, либо построить на основе данной информации новый объект, способ действия, закономерность, свойство, либо установить, подтвердить или опровергнуть истинность некоторого утверждения.

Ребенок с первых дней занятий в школе встречается с задачей. Текстовые задачи составляют около 40% материала учебника математики, и на их решение тратится значительная часть учебного времени. С начала и до конца обучения в школе математическая задача помогает ученику вырабатывать правильные математические понятия, глубже выяснять различные стороны взаимосвязей в окружающей его жизни, служит для раскрытия смысла арифметических действий, дает возможность применять изучаемые теоретические положения, способствует развитию памяти, мышления, внимания, воображения.

Какой же смысл вкладывают в понятие «математическая задача»? Математическая задача – это связный лаконичный рассказ, в который введены значения некоторых величин и предлагается отыскать другие неизвестные значения величин, зависимые от данных и связанные с ними определенными соотношениями, указанными в условии [2, 133].

В начальном курс математики задачам придается большое значение, так как, делая первые шаги в усвоении математики, младший школьник, безусловно, опирается на свой жизненный опыт, и очень важно, чтобы этот опыт был использован для осознания практической значимости математики. Являясь моделью реальных явлений, текстовые задачи помогают ему в этом, выполняя обучающую, развивающую и воспитывающую функции.

Обучающая функция задач заключается прежде всего в том, что в процессе их решения у школьников формируются или закрепляются те или иные математические знания и умения. Но для того, чтобы задача могла являться средством формирования новых математических знаний или их закрепления, ученику необходимо осознать суть самого понятия и овладеть действиями, которые входят в состав умения решать задачи. Они таковы:
  1. Прочитать и осознать ее текст, т.е. понять значение каждого слова и представить ту или иную ситуацию, которая в ней дана.
  2. Выделить условие и вопрос, известное и неизвестное.
  3. Установить связь между условием и вопросом, между данными и искомым, т.е. провести анализ ее текста, результатом которого явится выбор арифметического действия для ее решения.
  4. Записать решение и ответ.

В процессе овладения этими действиями развиваются речь, память, внимание, воображение и мышление учащихся, т.е. реализуется развивающая функция задач.

Воспитательная функция задач реализуется через их содержание и через организацию работы школьников с ними (индивидуальную, групповую, фронтальную), через различные методические приемы обучения их решению.

В процессе решения задач ученики знакомятся с важными в познавательном отношении фактами, тем самым расширяется их кругозор и устанавливается тесная связь между обучением и жизнью, осознается практическая значимость изучения математики в школе. Это оказывает влияние на формирование мировоззрения учащихся и их отношение к учению. Индивидуальная работа над задачей, организуемая с помощью различных методических приемов, способствует формированию таких качеств личности, как трудолюбие, настойчивость, упорство, самоконтроль и самооценка. Фронтальная и групповая формы работы оказывают положительное влияние на формирование отношений между учениками [5, 160-161].

Задача – это сформулированный словами вопрос, ответ на который может быть получен с помощью арифметических действий [1, 111]. Из самого определения задачи вытекает, что в ней обязательно должен быть заключен какой-то вопрос. Без вопроса задачи нет. Поскольку ответ на вопрос задачи должен быть получен в результате арифметических действий, очевидно, в ней должно заключаться требование узнать то или иное число (или числа) – искомое и, кроме того, в задаче должны быть указаны те числа, с помощью действий над которыми может быть найдено искомое. Поэтому обязательными элементами всякой арифметической задачи являются неизвестное (искомое) число (или несколько искомых чисел) и данные числа.

Основные элементы задачи – условие и вопрос. Числовые (или буквенные) данные представляют собой элементы условия. Искомое всегда заключено в вопросе. Однако в некоторых случаях задача формируется так, что вопрос может включить в себя часть условия или вся задача излагается в форме вопроса.

Все это необходимо учитывать при обучении детей решению задач. Один из важнейших моментов обучения состоит в том, чтобы дети научились самостоятельно выполнять первичный анализ текста задачи, отделяя известное от неизвестного. Существенно, чтобы они умели не только вычленить из задачи данные, но и объяснить, что обозначат каждое из содержащихся в ней число в контексте самой задачи, что сказано про то число, которое нужно найти. Важно, чтобы при первичном анализе внимание обращалось не только на выделение данных и искомого, но и на связи между ними, описанные в тексте задачи.

Процесс решения задачи – это переход от условия задачи к ответу на ее вопрос (выполнение требования, ответ на вопрос задачи или вывод о выполнении требования – результат процесса решения задачи). Задача считается решенной, если в результате некоторых операций с информацией, данной в задаче, вербально или в других знаковых системах сформулирован ответ на вопрос задачи, соответствующий условию задачи. Ответ на вопрос задачи считается соответствующим условию задачи, если информация, содержащаяся в нем, не противоречит никакой информации, данной в условии.

В процессе решения задачи выделяют пять этапов. Каждый этап решения есть сложное умственное действие, входящее в состав еще более сложного решения – решения задачи. Тогда каждый «прием выполнения» есть операция или совокупность операций соответствующего действия [В.А. Лебединцева]. Рассмотрим эти этапы:

I. Восприятие осмысление задачи.

Цель: понять задачу, т.е. установить смысл каждого слова, словосочетания, предложения и на этой основе выделить множества, отношения, величины, зависимости, известные и неизвестные, искомое, требование.

Приемы выполнения таковы:

1. Правильное чтение задачи (правильное прочтение слов и предложений, правильная расстановка логических ударений) в случае, когда задача задана текстом.
  1. Правильное слушание при восприятии задачи на слух.
  2. Правильное слушание при восприятии описанной задачи, т.е. создание зрительного, возможно, слухового и кинестетического образов.
  3. Разбиение текста на смысловые части.
  4. Переформулировка текста задачи (изменение текста или построения словесной модели): замена термина содержательным описанием; замена некоторых слов синонимами или другими словами, близкими по смыслу; изменение порядка слов и предложений; дополнение текста пояснениями и т.д.
  5. Построение материальной или материализованной модели: предметной (показ задачи на конкретных предметах); геометрической показ задачи с помощью графических фигур или предметных моделей фигур с использованием их свойств и отношений между ними); условно-предметной (рисунок); словесно-графической (схематическая краткая запись текста задачи); табличной.
  6. Постановка специальных вопросов:

− О чем говорится в задаче?

− Что известно в задаче?

− Что требуется узнать в задаче?

− Что обозначают слова …, словосочетания…, предложения….

II. Поиск плана решения.

Цель: составить план решения.

Приемы выполнения:
  1. Рассуждения «от вопроса к данным» или «от данных к вопросу» без построения графических схем.
  2. Рассуждения «от вопроса к данным» или «от данных к вопросу» с построением графической схемы.
  3. Замена неизвестного переменной и перевод текста на язык равенств или неравенств с помощью рассуждений «от вопроса к данным» или «от данных к вопросу».

Ш. Выполнение плана решения.

Цель: найти ответ на вопрос задачи, т.е. выполнить требование задачи.

Приемы и формы выполнения:
  1. Устное выполнение каждого пункта плана.
  2. Письменное выполнение каждого пункта плана:

а) арифметическое решение:

- в виде выражения с записью шагов по его составлению, вычислений и полученного результата этих выражений – равенства;

- в виде выражения преобразуемого после вычислений в равенство, без записи шагов по составлению выражения;

б) алгебраическое решение:

- в виде уравнения и его решения;

- через запись шагов составления уравнения и его решения;

в) графическое и геометрическое решение: графическое решение может быть геометрическим, если оно основано на геометрических свойствах изображения, и не геометрическим, если свойства геометрических фигур не используются:

- в виде чертежа или рисунка с представлением промежуточных шагов построения и измерения;

- в виде чертежа или рисунка без представления промежуточных шагов построения и измерения;

г) табличное решение:

- в виде таблицы с записью шагов по ее построению;

- в виде таблицы и ее заполнения без представления промежуточных шагов;

д) Логическое решение.

3. Выполнение решения путем практических действий с предметами: реальное или мысленное.

IV. Проверка решения.

Цель: установить, соответствуют ли процесс и результат решения образцу правильного решения.

Приемы выполнения:
  1. Прогнозирование результата (прикидка, установление границ ответа на вопрос задачи) и последующее сравнение хода решения с прогнозом. При несоответствии прогнозу – решение неверно. При соответствии − решение может быть как верным, так и неверным.
  2. Установление соответствия между результатом решения и условием задачи: введение в текст задачи вместо вопроса ответ на него, получение всех возможных следствий из полученного текста, сопоставление результатов друг с другом и с информацией, содержащейся в тексте. Если в результате будут обнаружены противоречивые утверждения, то задача решена неправильно. В противном случае – результат решения верен. Правильность хода не устанавливается.
  3. Решение другим методом или способом.
  4. Составление и решение обратной задачи.
  5. Сравнение с правильным решением – с образцом хода и (или) результата решения. При решении задачи тем же методом и способом, что и в имеющемся образце, возможно установление правильности как хода, так и результата решения.
  6. Обоснование каждого шага решения через соотнесение с более общими теоретическими положениями. Возможно установление правильности хода и результата решения.

V. Формулировка ответа на вопрос задачи .

Цель: дать ответ на вопрос задачи, т.е. подтвердить факт выполнения требования.

Формы и способы выполнения:
  1. Построение развернутого истинного рассуждения: «Так как …, то можно сделать вывод, что (формулируется ответ на вопрос задачи полным предложением в устной или письменной форме).
  2. Формулировка полного ответа на вопрос задачи полным предложением без обосновывающей части устно или письменно.
  3. Формулировка краткого ответа с помощью специальных знаков.

Итак, чтобы решить задачу, необходимо ознакомиться с ней и понять ее, затем составить план решения, после чего выполнить его, сформулировать ответ на вопрос задачи, проверить ход и результат решения.

Проблемой развития методики обучения решению задач занимались и занимаются многие методисты, в числе которых можно отметить М. А. Бантову, Г. В. Бельтюкову, Н. Б.Истомину, М. И. Моро, А. С. Пчелко, А. А. Свечникова и многих других. Особое внимание в их работах уделяется методике работы над простыми задачами, так как именно простые задачи являются средством ознакомления с математическими отношениями и понятиями, служат для раскрытия смысла арифметических действий, а также обладают огромными возможностями для развития памяти, мышления, воображения. Использование задач способствует формированию основ математического мировоззрения, позволяет ребенку глубже выяснять различные стороны взаимосвязей в окружающей его жизни, дает возможность применять изучаемые теоретические положения, позволяет устанавливать разнообразные числовые отношения в наблюдаемых явлениях. Другими словами, задачи и их решение дают ребенку ответ на вопрос: «Для чего нужна математика?» Чем выше эффективность методов обучения решению задач, тем выше интерес учащихся к математике и уровень развития математических знаний, умений и навыков вообще.

Н. Б. Истомина рассматривает понятие «решение задачи» с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата. С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который, в свою очередь, тоже можно рассматривать с различных точек зрения. Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, которые входят в тот или иной способ.

Можно сделать вывод, что цели решения задач сводятся к следующим:
  1. Установить причинно-следственные связи и раскрыть функциональную зависимость между величинами, входящими в условие задачи.
  2. Научиться умению логически правильно рассуждать и делать обоснованные умозаключения при выяснении хода решения задач.
  3. Обоснованно выбирать арифметические действия и проводить их безошибочно.
  4. Ознакомиться с решением задач определенного вида.

Таким образом, учитель должен стремиться к тому, чтобы каждая задача стала наиболее разносторонним источником знаний и представлений, давала бы наиболее полный поток информации, поступающие и в мозг ученика. Необходимо ориентировать его на то, чтобы при решении задачи он почерпнул из нее все возможные сведения, способствующие его развитию, его продвижению вперед по пути совершенствования мышления, по пути овладения новыми знаниями.


Литература

1. Моро, М. И. Методика обучения в I–III классах : пособие для учителя / М. И. Моро, А. М. Пышкало. – М. : Просвещение, 1978. – 336 с.

2. Свечников, А. А. Решение математических задач в I–III классах / А. А. Свечников. – М. : Просвещение, 1976.

3. Смолеусова, Т. В. Этапы, методы и способы решения задачи / Т. В. Смолеусова // Начальная школа. – 2003. – № 12. – С. 62-67.

4. Стойлова, Л. П. Основы начального курса математики / Л. П. Стойлова, А. М. Пышкало. – М. : Просвещение, 1988. – 319 с.

5. Теоретические основы методики обучения математики в начальных классах / под ред. Н. Б. Истоминой. – М.-Воронеж : институт практической психологии ; НПО «МОДЖ», 1996. – 226 с.





Беляева Зоя Михайловна,
доцент кафедры РЯМП,
Бычков Вениамин Иванович,
доцент кафедры РЯМП

О Концепции обучения русскому языку в 1-4 классах

общеобразовательных школ Чувашской Республики

с родным (нерусским) языком обучения

Модернизация системы образования требует перехода от традиционной установки на формирование преимущественно «знаний, умений, навыков» к воспитанию качеств личности, необходимых для жизни в новых условиях открытого общества. Приоритетной целью образования в современной школе становится развитие личности, готовой к правильному взаимодействию с окружающим миром, к самообразованию и саморазвитию.

Анализ состояния двуязычия и изучение мирового опыта развития национальных систем образования позволяет высказать положение о том, что в условиях многонациональной России моделью национальной школы может быть национальная двуязычная школа, в которой в качестве обучения в школе первой ступени используется родной язык, а русский язык является учебным предметом. Знание русского языка призвано:

-сохранять единое образовательное пространство Российской Федерации;

- обеспечить функционирование русского языка как государственного и языка межнационального общения;

- координировать в условиях двуязычия (родной и русский языки) взаимосвязанное обучение родному и русскому языкам, имеющим статус государственных в Чувашской Республике.

В современных условиях национальная чувашская школа является двуязычной школой, где и родной, и русский языки реализуются во всех функциональных сферах, обеспечивая овладение как родной, так и русской речью. Функциональное двуязычие предполагает использование и родного, и русского языка в качестве средства общения, оформления мысли, передачи информации. Русский язык является языком изучения других предметов в среднем и старшем звене, уровень усвоения которых в значительной мере предопределяет успешность всего последующего обучения. Следующий приоритет русского языка в национальной школе диктуется многонациональностью российского народа: в качестве средства межнационального общения русский язык позволяет воспитывать уважение к культуре и языку других народов.