Если использовать разности высших порядков вплоть до n-го, то разностное уравнение 1

  1   2   3   4   5   6   7

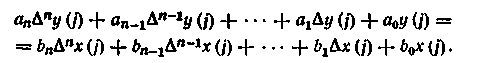
Описанные способы аппроксимации дифференциальных уравнений разностными дают удовлетворительные результаты только в тех случаях, когда период квантования t₀ мал по сравнению с наименьшей постоянной времени объекта. В систе­мах управления промышленными технологическими объектами это условие обычно выполняется вследствие большой инерцион­ности объектов и высокого быстродействия современных управ­ляющих вычислительных машин, позволяющих реализовать опрос всех контуров регулирования с малым периодом.

Применение средств вычислительной техники для управле­ния значительно расширило возможности реализации различ­ных законов управления и регулирования, структура и пара­метры которых определяются в результате оптимизации систе­мы управления. Однако наиболее распространены в системах непосредственного цифрового управления алгоритмы, разрабо­танные как аналоги непрерывного ПИД-регулятора. Это по­зволяет использовать накопленный опыт работы с аналоговы­ми регуляторами и применять хорошо известные правила вы­бора параметров.

Простейший способ получения алгоритма управления по ПИД-закону состоит в переходе от интегро-дифференциального уравнения непрерывного регулятора к разностному уравнению (в соответствии с изложенными выше правилами).

Если уравнение ПИД-регулятора записать в виде (рис. 1.3)

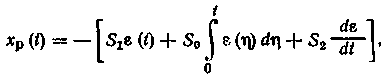
то при интегрировании по методу прямоугольников для перио­да квантования /о получим разностное уравнение

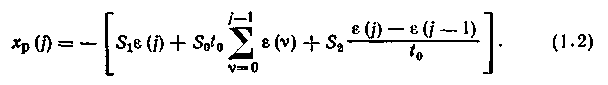
Полученный алгоритм, называемый позиционным, неудобен для реализации в УВМ, так как для формирования управляю­щего воздействия требуется, кроме текущего значения сигнала ошибки помнить все предыдущие значения — от е(0) до е(j-1).

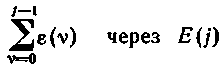
Позиционный алгоритм можно модернизировать, сделав его

рекуррентным. Для этого обозначим


24






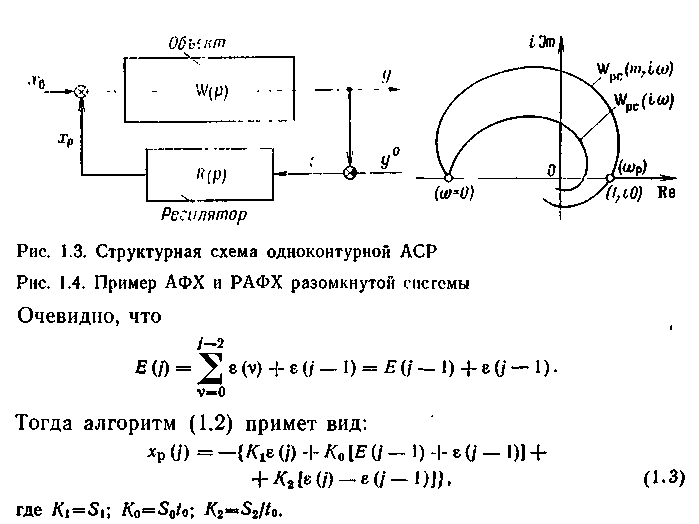
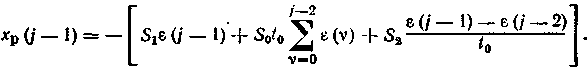
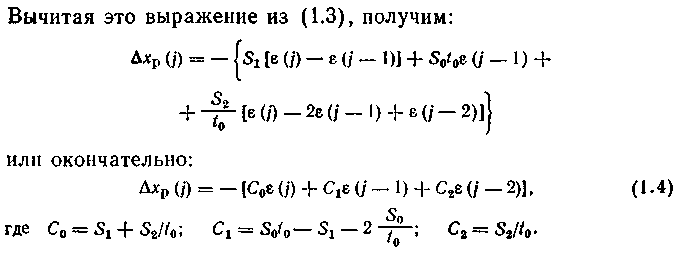
Чтобы вывести рекуррентный («скоростной») алгоритм, по которому текущее значение управления Xp(j) вычисляется как сумма предыдущего значения x_p(j—1) и поправки &x_p(j), за­пишем выражение для x_p(j—1):

При этом рекуррентный алгоритм для ПИД-регулятора за­пишется в виде:



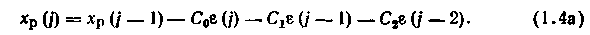
При малых значениях периода квантования t₀ переходные процессы в дискретной и непрерывной АСР практически сов­падают, поэтому выбор параметров настроек дискретных регу-


25


ляторов проводят по тем же соотношениям, что и непрерыв­ных. Например, для ПИД-регулятора параметры настроек K₁, Ко, K₂ или Со, С₁, С₂, при малых значениях to можно вычис­лить по S₁, S₀, S₂, используя формулы (1.3) или (1.4), в зави­симости от выбранного алгоритма; значения же настроек не­прерывного регулятора находят одним из рассмотренных ниже методов (см. разд. 1.2 и 1.4). Для дискретных П- и ПИ-регу-ляторов можно воспользоваться теми же формулами (1.3), (1.4), полагая в них равными пулю коэффициенты So и S₂ для П-ре-гулятора или S₂ — для ПИ-регулятора.

1.2. РАСЧЕТ НАСТРОЕК РЕГУЛЯТОРОВ В ОДНОКОНТУРНЫХ АСР

При определении настроек регуляторов в качестве показателя оптимальности системы регулирования обычно выбирают ин­тегральный критерий качества (например, интегральный квад­ратичный критерий) при действии на объект наиболее тяже­лого возмущения с учетом добавочного ограничения на запас устойчивости системы. В практических расчетах запас устойчи­вости удобно характеризовать показателем колебательности системы; его значение для систем, имеющих интегральную со­ставляющую в законе регулирования, определяется максимумом амплитудно-частотной характеристики замкнутой системы ре­гулирования.

В дальнейшем под оптимальными будем понимать настрой­ки регулятора, обеспечивающие заданную степень колебатель­ности т* процесса регулирования при минимуме интегрального квадратичного критерияJ_кв.

Среди инженерных методов расчета настроек регуляторов одни являются более точными, но трудоемкими для ручного счета, другие — простыми, по приближенными. Подробно эти методы изложены в различных пособиях и монографиях [19,23, 42—49]. Наиболее распространенными способами, отражающи­ми методику точного и приближенного расчета настроек, яв­ляются метод расширенных частотных характеристик (РЧХ) и метод незатухающих колебаний (Циглера — Никольса). Метод РЧХ. По этому методу расчетные формулы для настроек регуляторов получают из условия, аналогичного критерию Найквиста: если разомкнутая система имеет степень колеба­тельности не ниже заданной, то замкнутая система будет об­ладать заданной степенью колебательности в том случае, ког­да расширенная амплитудно-фазовая характеристика (РАФХ) разомкнутой системы W_pс(m, iw) проходит (рис. 1.4) через точку (1, i0), т. е.




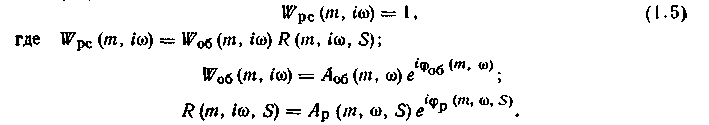
26

Уравнение (1.5) равносильно двум уравнениям, записанным относительно расширенных амплитудно-частотных и фазоча-стотных характеристик объекта и регулятора:



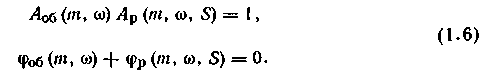
Для заданных частотных характеристик объекта и выбран­ного закона регулирования при решении системы уравнений (1.6) находит вектор настроек регулятора S, обеспечивающих заданную степень колебательности на каждой частоте.

Для регуляторов с одним параметром настройки, у которых фр(m, w) не зависит от параметра S, из второго уравнения (1.6) находят рабочую частоту w_р, а из первого — параметр настройки S*.

Для П-регулятора с передаточной функцией R(p)= - S₁ рабочую частоту w_р находят из уравнения

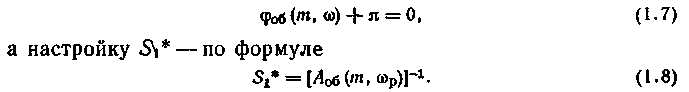
Для И-регулятора с передаточной функцией R(p) = - S₀/p частоту w_р определяют из уравнения

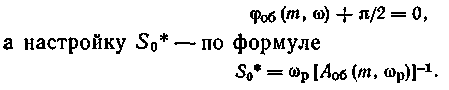
Для регуляторов с двумя параметрами настроек по урав­нениям (1.6) в плоскости параметров настроек рассчитывают линию равной степени колебательности (рис. 1.5 а, б) для ин­тервала частот, заданного условием



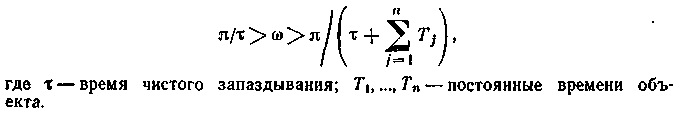
Для ПИ-регулятора с передаточной функцией R(p)= - Si - - So/p система уравнений (1.6) приводит к решению в виде:



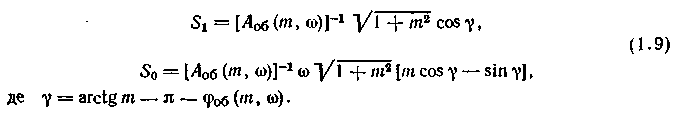
Для ПД-регулятора с передаточной функцией R(p)= - Si - - S₂p аналогичные формулы для настроек запишутся в виде:




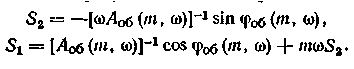
27

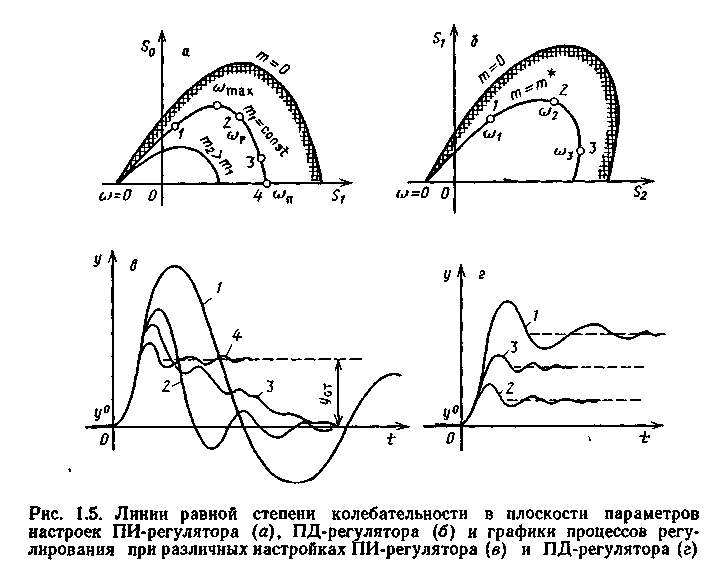
Разным точкам на кривой равной степени колебательности соответствуют различные процессы регулирования (рис. 1.5 в, г).

Рабочую частоту (см. рис. 1.5 а) выбирают из условий



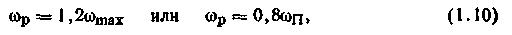
соответствующих минимуму J_кв-

Для ПИД-регулятора с тремя параметрами настройки и передаточной функцией R(p)= - S₁ - So/p - S₂p из системы уравнений (1.6) можно найти настройки S\ и So как функции S₂:



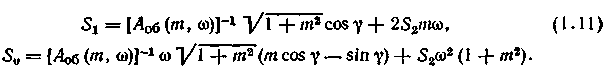
Оптимальные настройки регулятора рассчитывают следую­щим образом. Задаваясь различными значениями S₂, по фор­мулам (1.11) находят линии равной степени колебательности в плоскости параметров S₁So (рис. 1.6а). Затем рассчитывают переходные процессы и по минимуму J_кв выбирают оптималь­ные S₁*(S₂), S₀*(S₂) при каждом значении S₂ (обычно они соответствуют точке вблизи вершины кривой равной степени колебательности). Далее моделируют переходные процессы для каждого варианта настроек S₂, S₁*(S₂), S₀*(S₂) и по ми-


28

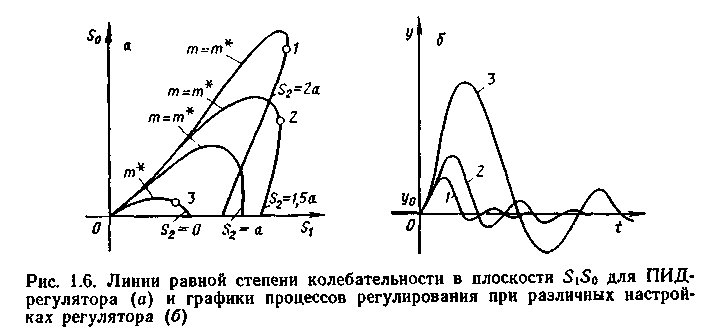
нимумуJкв выбирают оптимальное значение S₂* и соответ­ствующие ему S₁*, So*. На рис. 1.66 приведены примеры про­цессов регулирования при различных значениях настроек ПИД-регулятора.

Метод незатухающих колебаний. В соответствии с этим мето­дом расчет настроек ПИ- или ПИД-регуляторов проводят в два этапа: 1 — расчет критической настройки пропорциональ­ной составляющей S₁^KP(S₀=S₂=0), при которой АСР будет находиться на границе устойчивости, и соответствующей ей w_кр; 2 — определение по s₁^кр и w_кр оптимальных настроек S₁*, S₀*, S₂*, обеспечивающих степень затухания фи=0,8—0,9.

Уравнения для расчета S₁^Kp и соответствующей ей частоты w_КР получают из уравнений (1.7), (1.8) при m=0:



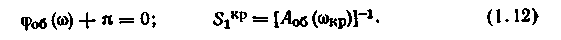
Оптимальные настройки ПИ- и ПИД-регуляторов находят по следующим формулам: для П-регулятора



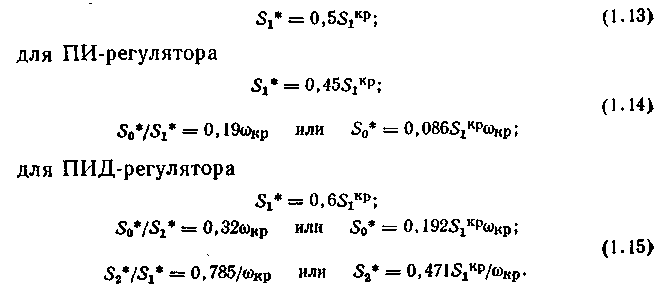
Метод Циглера — Никольса лежит в основе многих методов настройки дискретных ПИД-регуляторов. В частности, если


29


рекуррентный алгоритм управления, соответствующий анало­говому ПИД-закону, имеет вид




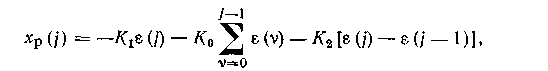
то для больших значений периода квантования /о параметры настройки K₁*, Ко*, K₂* могут быть найдены по следующим формулам [23]:

для П-регулятора



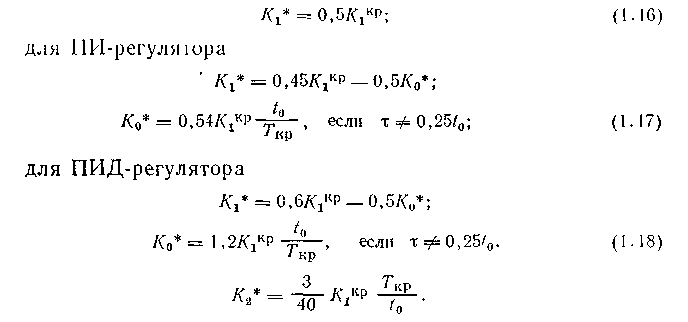
В уравнениях (1.16) — (1.18) K₁^кр и Т_кр — коэффициент при П-составляющей закона управления и период колебаний вы­ходной координаты, соответствующие режиму незатухающих колебаний АСР.

1.3. РАСЧЕТ НАСТРОЕК РЕГУЛЯТОРОВ В МНОГОКОНТУРНЫХ АСР

Удовлетворительное качество регулирования в простейшей од­ноконтурной системе с использованием стандартных законов регулирования можно обеспечить лишь при благоприятных динамических характеристиках объекта. Однако большинству промышленных объектов химической технологии свойственны значительное чистое запаздывание и большие постоянные вре­мени. В таких случаях даже при оптимальных настройках ре­гуляторов одноконтурные АСР характеризуются большими динамическими ошибками, низкой частотой регулирования и длительными переходными процессами. Для повышения каче­ства регулирования необходим переход от одноконтурных АСР к более сложным системам, использующим дополнительные (корректирующие) импульсы по возмущениям пли вспомога­тельным выходным координатам. Такие системы кроме обыч­ного стандартного регулятора содержат вспомогательные


30





регулирующие устройства — динамические компенсаторы или дополнительные регуля­торы.

В зависимости от характе-

ра корректирующего импульса различают следующие много-коигуриыс АСР: комбинированные, сочетающие обычный замк­нутый контур регулирования с дополнительным каналом воз­действия, по которому через динамический компенсатор вводится импульс по возмущению; каскадные — двухконтурные замкнутые АСР, построенные па базе двух стандартных регу­ляторов и использующие для регулирования кроме основной выходной координаты дополнительный промежуточный выход; с дополнительным импульсом по производной от промежуточ­ной выходной координаты.

1.3.1. Комбинированные АСР

Комбинированные системы регулирования применяют при ав­томатизации объектов, подверженных действию существенных контролируемых возмущений.

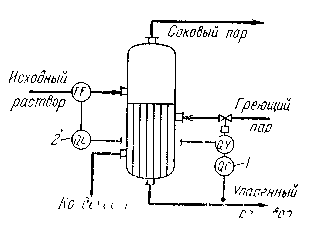
На рис. 1.7 приведен фрагмент функциональной схе­мы автоматизации выпарной установки, в которой одним из наиболее сильных возмущений является расход питания. Основ­ная задача регулирования — стабилизация концентрации упа­ренного раствора за счет изменения расхода греющего пара — выполняется регулятором 1. Кроме сигнала регулятора, на кла­пан, регулирующий подачу пара, через динамический компен-

сатор 2 поступает кор­ректирующий импульс по расходу питания.

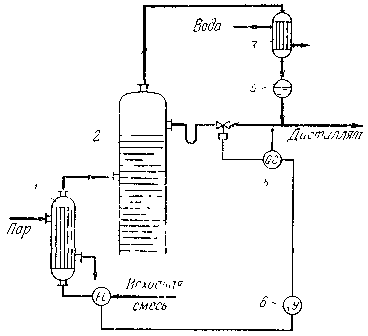
На рис. 1.8 приведен пример комбинированной АСР состава дистиллята в ректификационной ко­лонне. Стабилизация со-




31


става дистиллята обеспечивается регулятором 5 путем измене­ния подачи флегмы на орошение колонны. Для повышения качества регулирования в системе предусмотрена автоматиче­ская коррекция задания регулятору 5 в зависимости от одного из основных возмущений в процессе — расхода разделяемой смеси. Корректирующим импульс на задание регулятору по­ступает через динамический компенсатор 6".

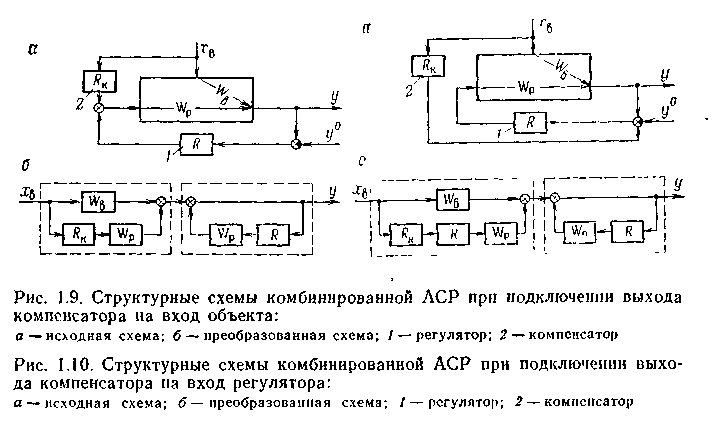
Рассмотренные примеры иллюстрируют два способа по­строения комбинированных АСР. Как видно из структурных схем (рис. 1.9 и 1.10), обе системы регулирования обладают общими особенностями: наличием двух каналов воздействия на выходную координату объекта и использованием двух коп-туров регулирования — замкнутого (через регулятор 1) и разо­мкнутого (через компенсатор 2). Отличие состоит лишь в том, что во втором случае корректирующий импульс от компенса­тора поступает не на вход объекта, а на вход регулятора.

Введение корректирующего импульса по наиболее сильно­му возмущению позволяет существенно снизить динамическую ошибку регулирования при условии правильного выбора и расчета динамического устройства, формирующего закон изме­нения этого воздействия.

Основой расчета подобных систем является принцип инва­риантности: отклонение выходной координаты системы от за­данного значения должно быть, тождественно равным нулю при любых задающих или возмущающих воздействиях.

Для выполнения принципа инвариантности необходимы два условия: идеальная компенсация всех возмущающих воздей­ствий и идеальное воспроизведение сигнала задания. Очевид­но, что достижение абсолютной инвариантности в реальных системах регулирования практически невозможно. Обычно




32

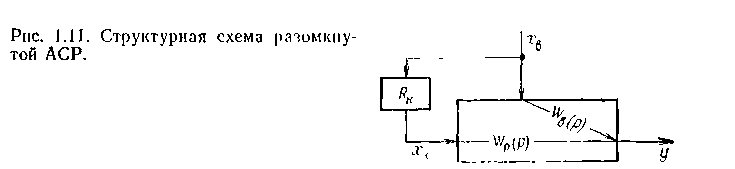
ограничиваются частичной инвариантностью по отношению к наиболее опасным возмущениям. Рассмотрим условие инва­риантности разомкнутой и комбинированной систем регулиро­вания по отношению к одному возмущающему воздействию. Условие инвариантности разомкнутой и комбинированной АСР. Рассмотрим условие инвариантности разомкнутой системы (рис. 1.11): y(t)=0.

Переходя к изображениям по Лапласу Хв(р) и Y(p) сигна­лов х_в(t) н y(t), перепишем это условие с учетом передаточных функций объекта по каналам возмущения Wв(p) и регулирова­ния Wp(p) и компенсатора R_K(p):



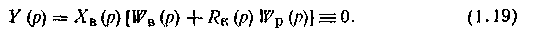
При наличии возмущения [X_B(p) <>0] условие инвариантности (1.19) выполняется, если



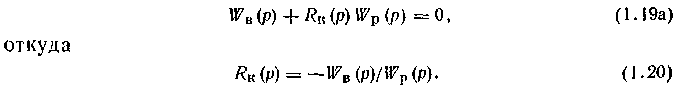
Таким образом, для обеспечения инвариантности системы регулирования по отношению к какому-либо возмущению не­обходимо установить динамический компенсатор, передаточная функция которого равна отношению передаточных функций объекта по каналам возмущения и регулирования, взятому с обратным знаком.

Выведем условия инвариантности для комбинированных АСР. Для случая, когда сигнал от компенсатора подается на вход объекта (см. рис. 1.9 а), структурная схема комбиниро­ванной АСР преобразуется к последовательному соединению разомкнутой системы и замкнутого контура (см. рис. 1.96), передаточные функции которых соответственно равны:




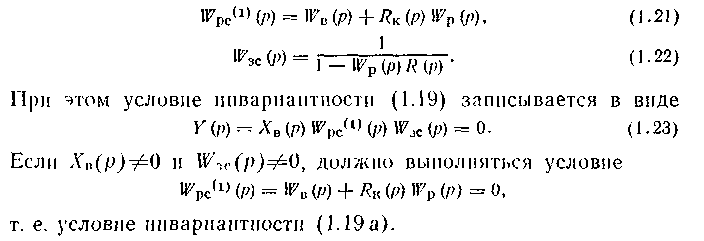
33

При использовании комбинированной системы регулирова­ния (см. рис. 1.10 а) вывод условий инвариантности приводит к соотношениям (см. рис. 1.106):



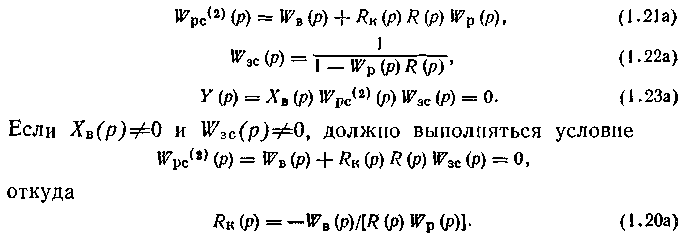
Таким образом, при подключении выхода компенсатора на вход регулятора передаточная функция компенсатора, получен­ная из условия инвариантности, будет зависеть от характери­стик не только объекта, но и регулятора.

Условия физической реализуемости инвариантных АСР. Одной из основных проблем, возникающих при построении инвариант­ных систем регулирования, является их физическая реализуе­мость, т. е. реализуемость компенсатора, отвечающего усло­виям (1.20) или (1.20 а).

В отличие от обычных промышленных регуляторов, струк­тура которых задана и требуется лишь рассчитать их настрой­ки, структура динамического компенсатора полностью опреде­ляется соотношением динамических характеристик объекта по каналам возмущения и регулирования и может оказаться очень сложной, а при неблагоприятном соотношении этих характе­ристик - физически нереализуемой.

«Идеальные» компенсаторы физически нереализуемы в сле­дующих двух случаях.

1. Если время чистого запаздывания по каналу регулирова­ния больше, чем по каналу возмущения. В этом случае идеаль­ный компенсатор должен содержать звено упреждения, так как если



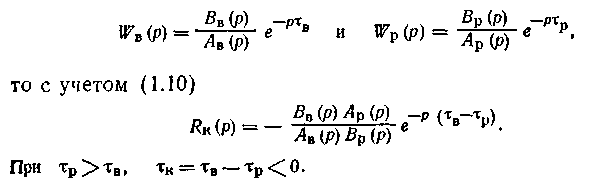
2. Если в передаточной функции компенсатора степень по­линома в числителе больше, чем степень полинома в знамена­теле. В этом случае компенсатор должен содержать идеальные дифференцирующие звенья. Такой результат получается при


34



Таким образом, условие физической реализуемости инва­риантной АСР заключается в том, чтобы выполнялись соот­ношения



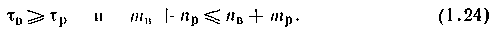
Пример. Рассмотрим систему регулирования температуры в химическом реакторе с перемешивающим устройством, в котором протекает экзотерми­ческая реакция (рис. 1.12). Пусть основной канал возмущения — «расход реакционной смеси — температура в реакторе» — аппроксимируется двумя апериодическими звеньями первого порядка, а канал регулирования — «рас­ход хладоагента — температура в реакторе» — тремя апериодическими звенья­ми первого порядка:



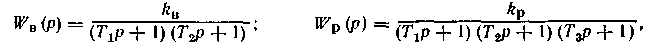
где T₁, Т₂, Т₃ — наибольшие постоянные времени основных тепловых емко­стей реактора, термометра и охлаждающей рубашки.

Для построения инвариантной системы регулирования необходимо вве­сти компенсатор с передаточной функцией



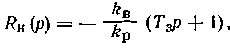
который физически нереализуем, так как в данном случае нарушается ус­ловие (1.24), и компенсатор должен содержать идеальное дифференцирую­щее звено.

Техническая реализация инвариантных АСР. При практической реализации разомкнутых и комбинированных АСР обычно до­биваются приближенной инвариантности системы по отноше­нию к рассматриваемому возмущению в наиболее опасном диапазоне частот. При этом реальный компенсатор выбирают из числа наиболее легко реализуемых динамических звеньев, параметры которых рассчитывают из условия близости частот-