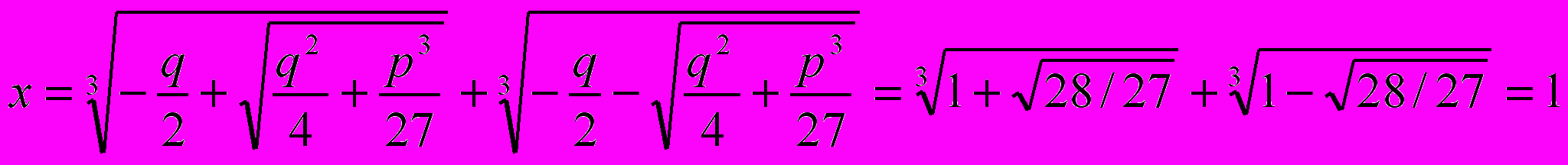Решение кубического уравнение в общем виде. От общего кубического уравнения к упрощённому
| Вид материала | Решение |
СодержаниеПервый вариант решения упрощённого кубического уравнения. Второй вариант решения упрощённого кубического уравнения. |
- В. Ю. Калугина, студент; Н. Н. Михайлова,, 32.84kb.
- Удк 539. 2 Пленки алмаза и кубического нитрида бора, 75.03kb.
- Моу сош №5 Реферат Комплексные числа и действия с ними, 103.44kb.
- Решение кубичных уравнений, 38.76kb.
- П. В. Чулков, «Уравнения и неравенства в школьном курсе математики, лекции 1-4», стр, 8.44kb.
- Содержание уравнения математической физики (нм-3) Уравнения математической физики (нп-3), 92.05kb.
- Лекция магнитооптические явления, Гиротропия, 119.87kb.
- Урок в 7 классе по теме: «Системы линейных уравнений в решении алгебраических задач», 97.42kb.
- Дифференциальные эллиптические уравнения второго порядка. Слабое решение. Обобщенное, 106.04kb.
- Статья Тема: «Уравнения высших степеней с параметрами», 55.64kb.
Решение кубического уравнение в общем виде.
От общего кубического уравнения к упрощённому.
Покажем, что любое кубическое уравнение можно привести к виду
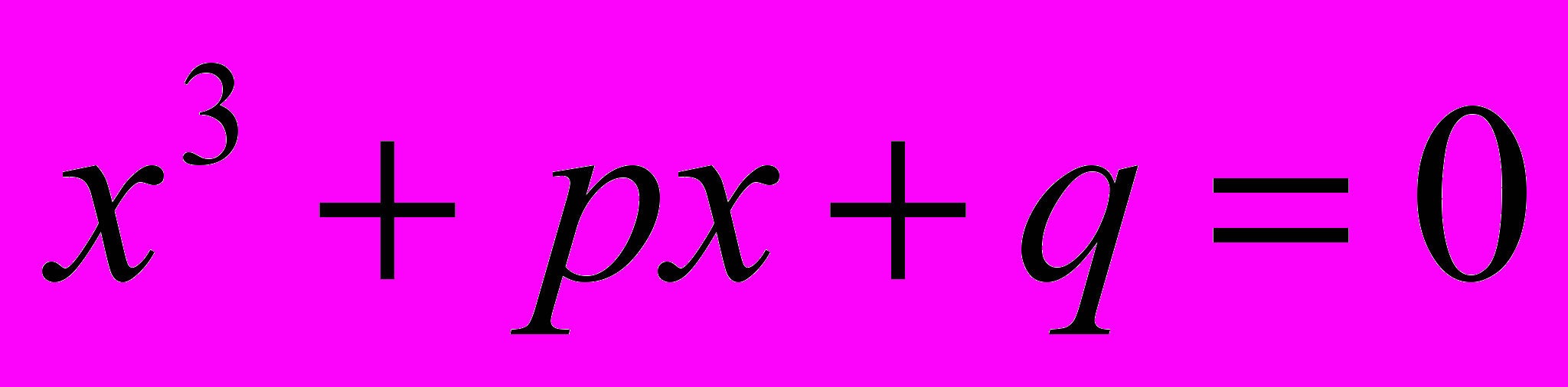
В самом общем виде кубическое уравнение задаётся в виде.
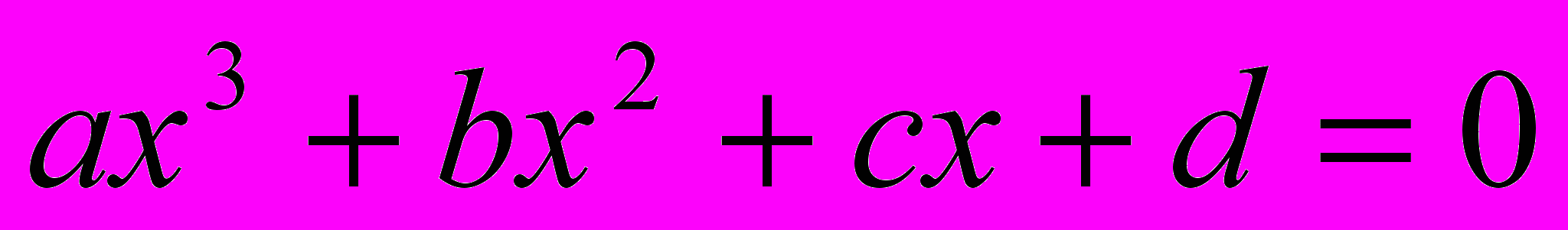, где 
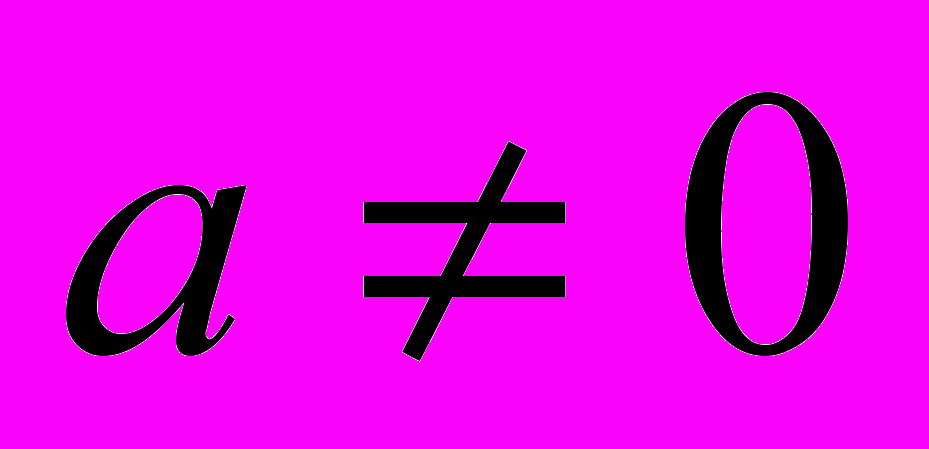(1)Заменой
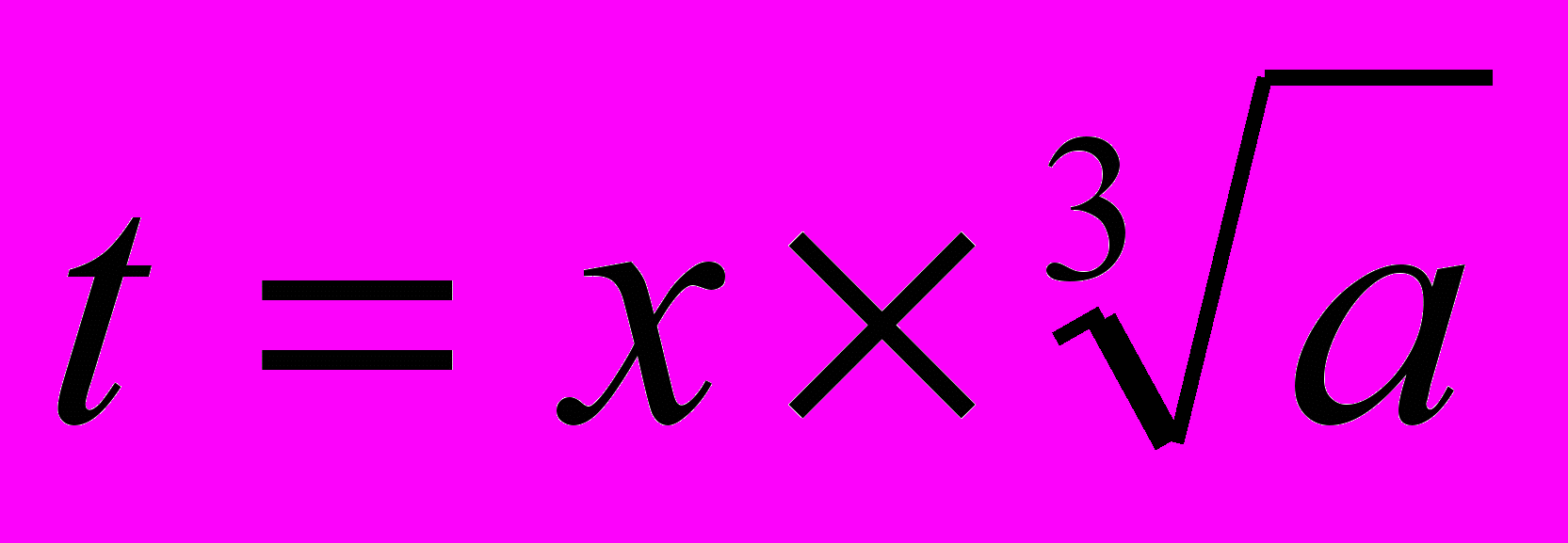уравнение 1 приведётся к виду 
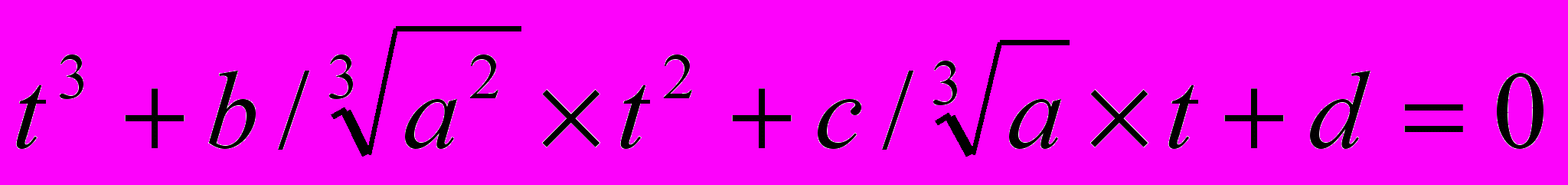, таким образом уравнение (1) при велось к виду 
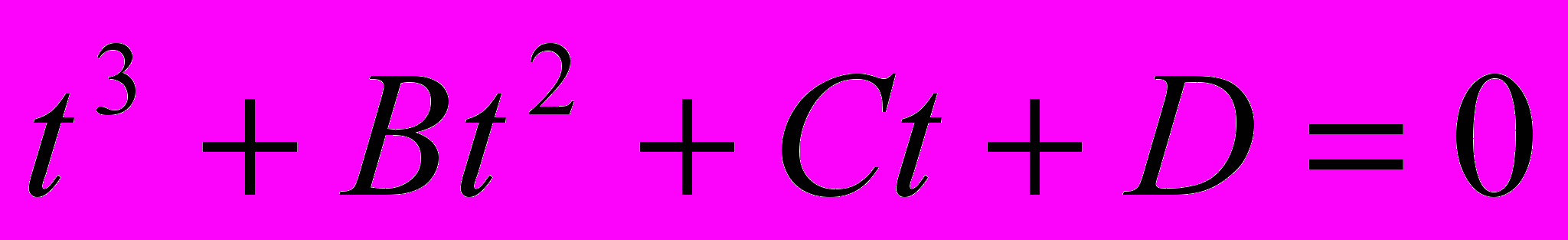(2)Теперь делаем новую замену
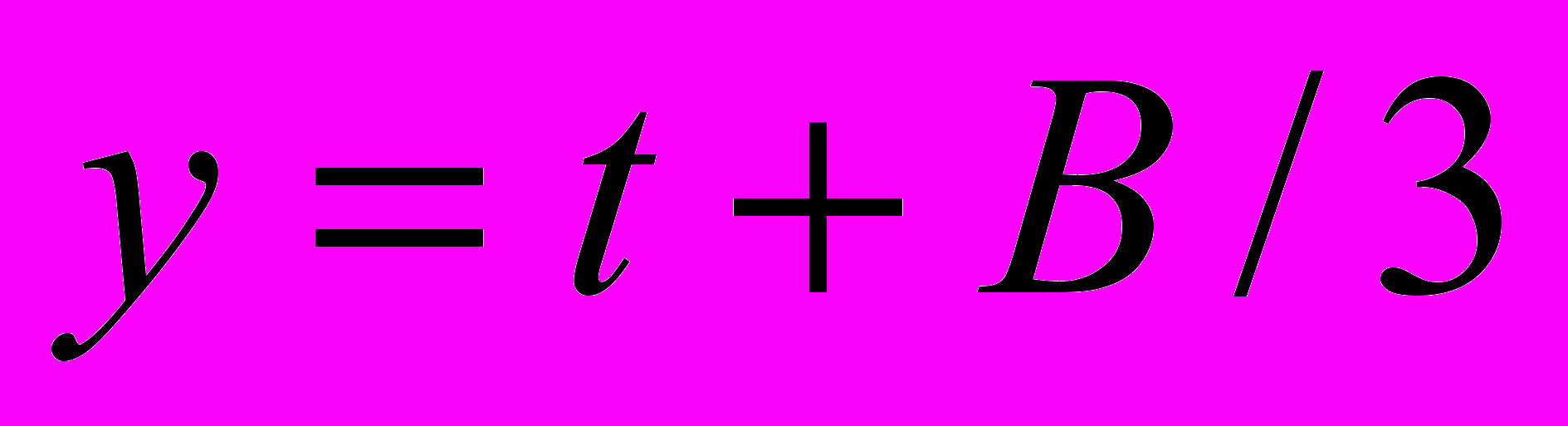
Таким образом уравнение (2) приведётся к виду
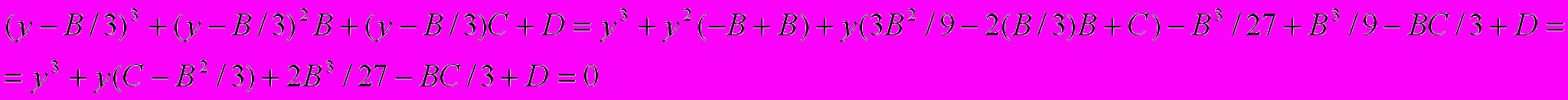Обозначая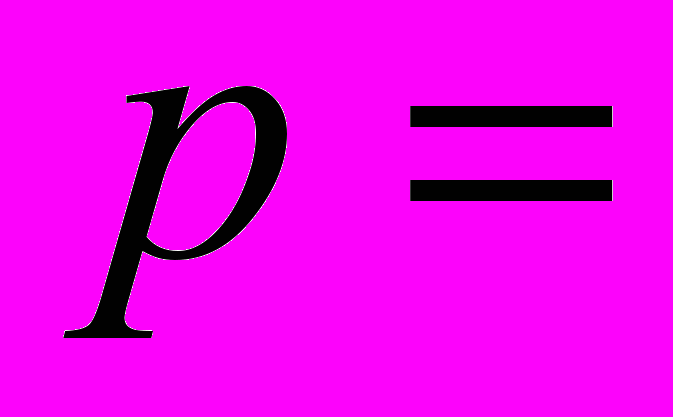 
, 
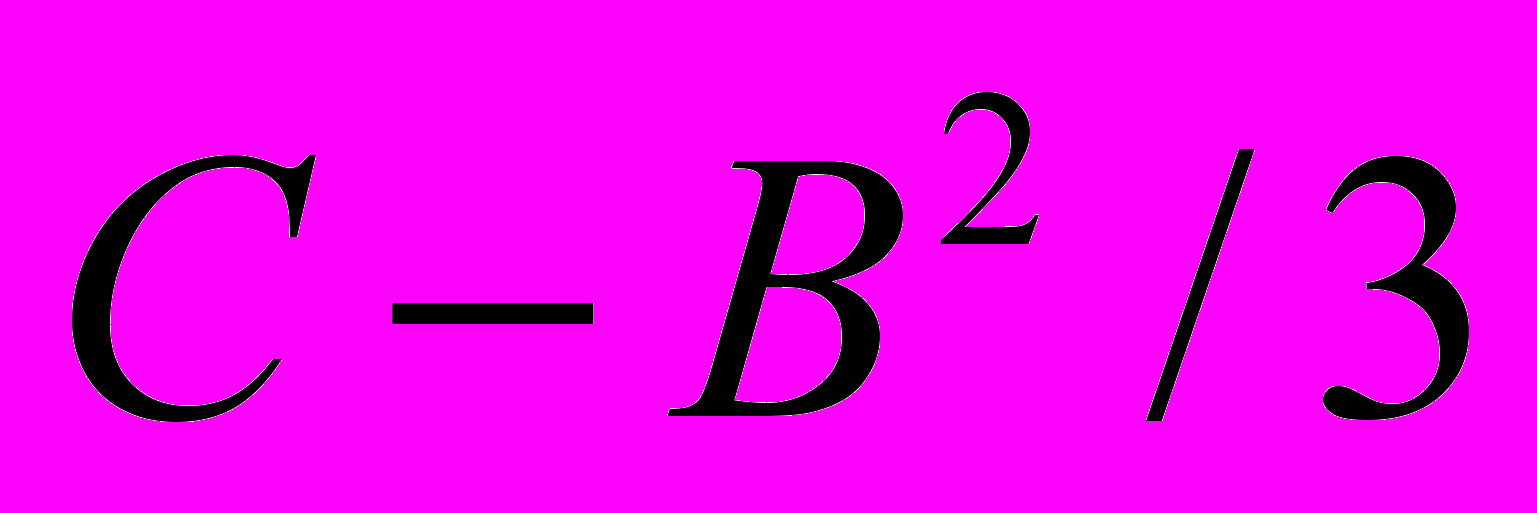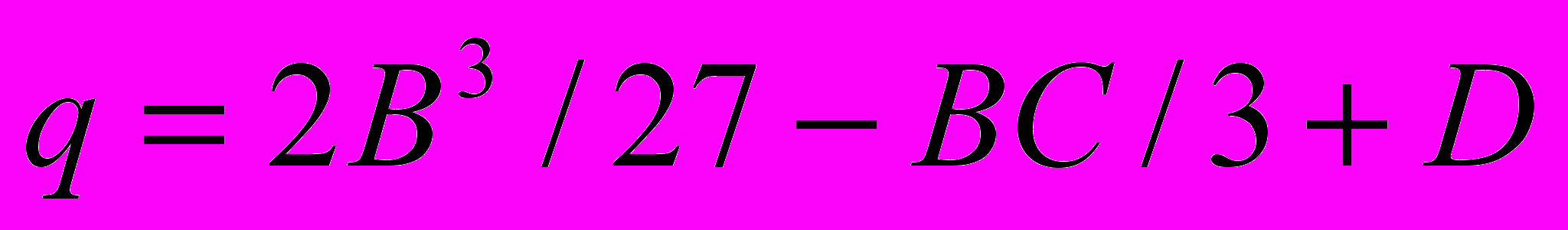, видим, что начальное уравнение (1) привелось к виду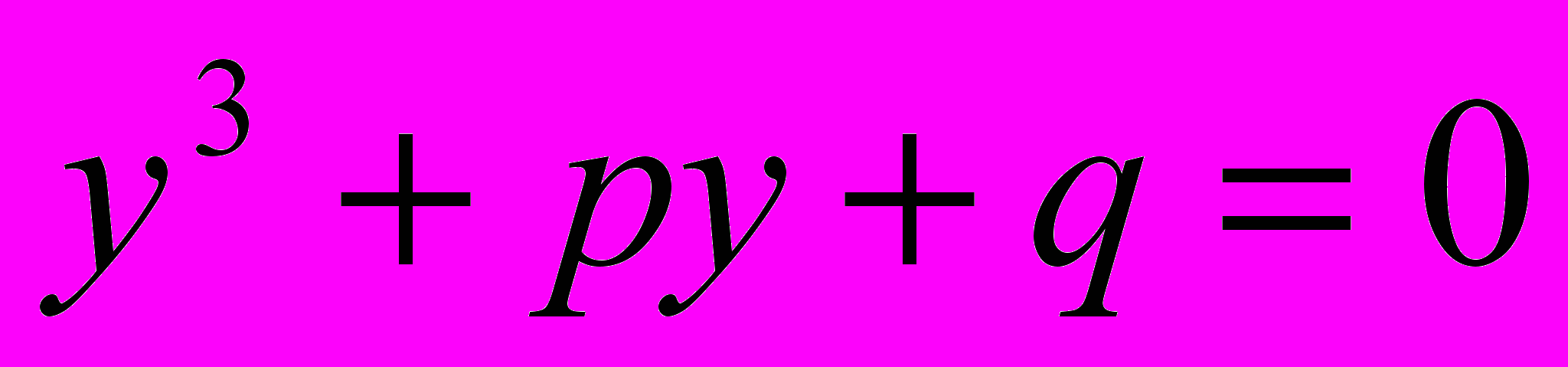 
Первый вариант решения упрощённого кубического уравнения.
Решим уравнение
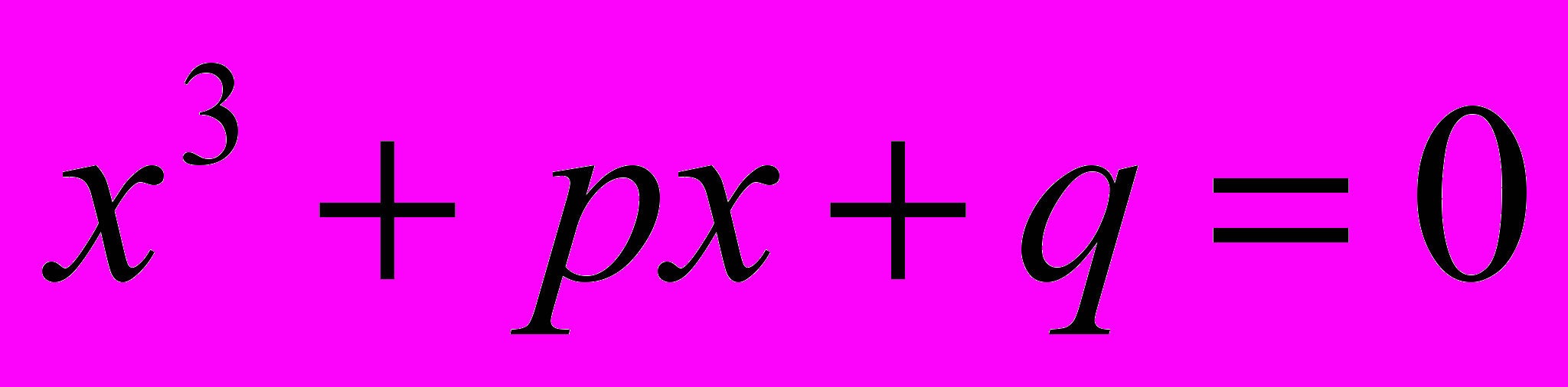(3). Для этого представим 
в виде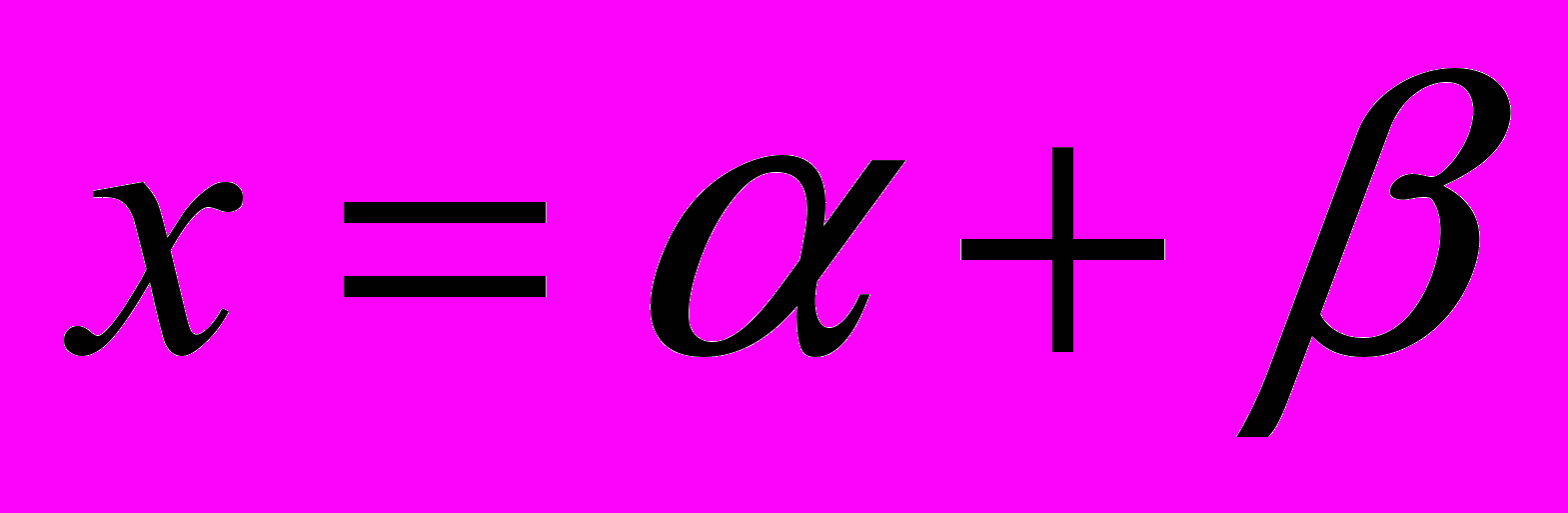 
и найдём 
и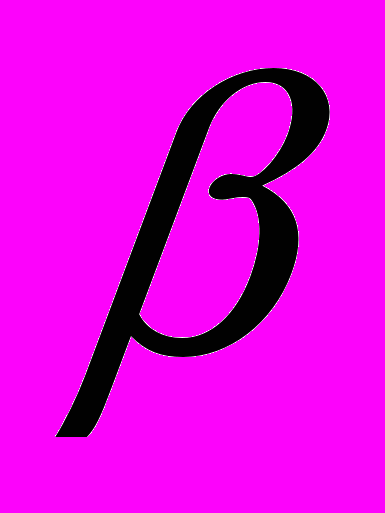 
. Тогда уравнение (3) запишется в виде
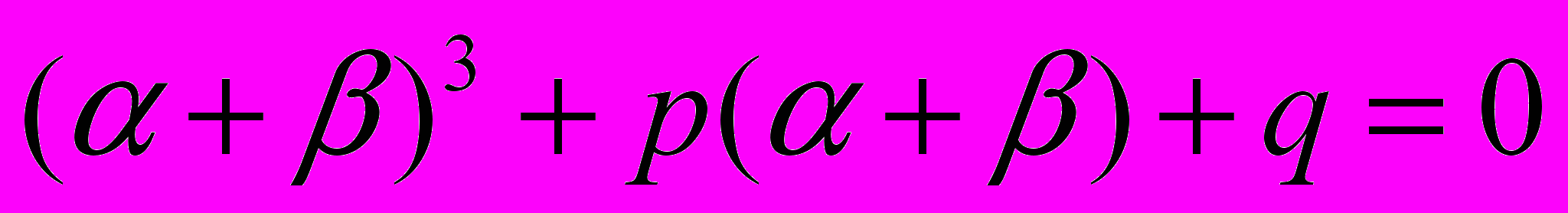. Получим, что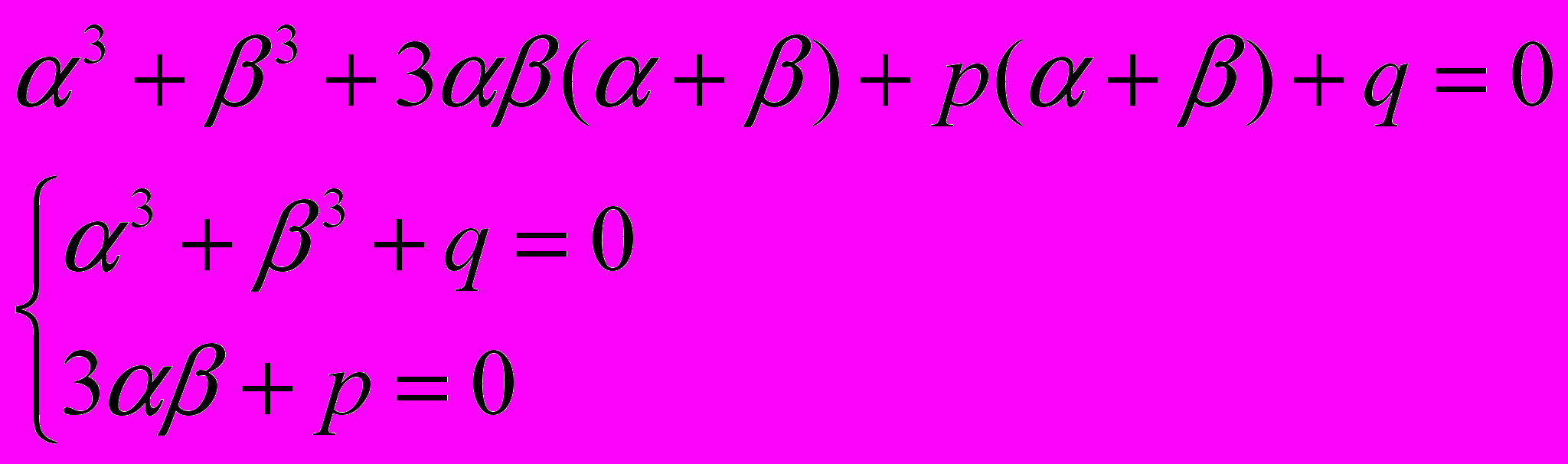 
Теперь решим эту систему уравнений относительно
и .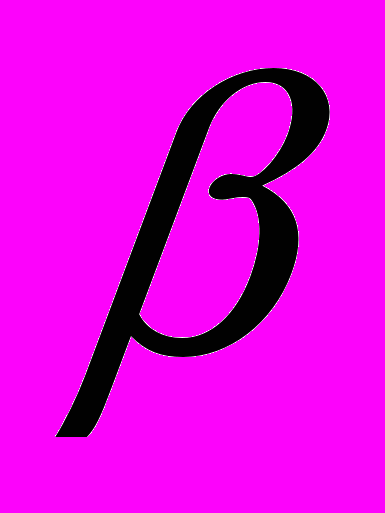 
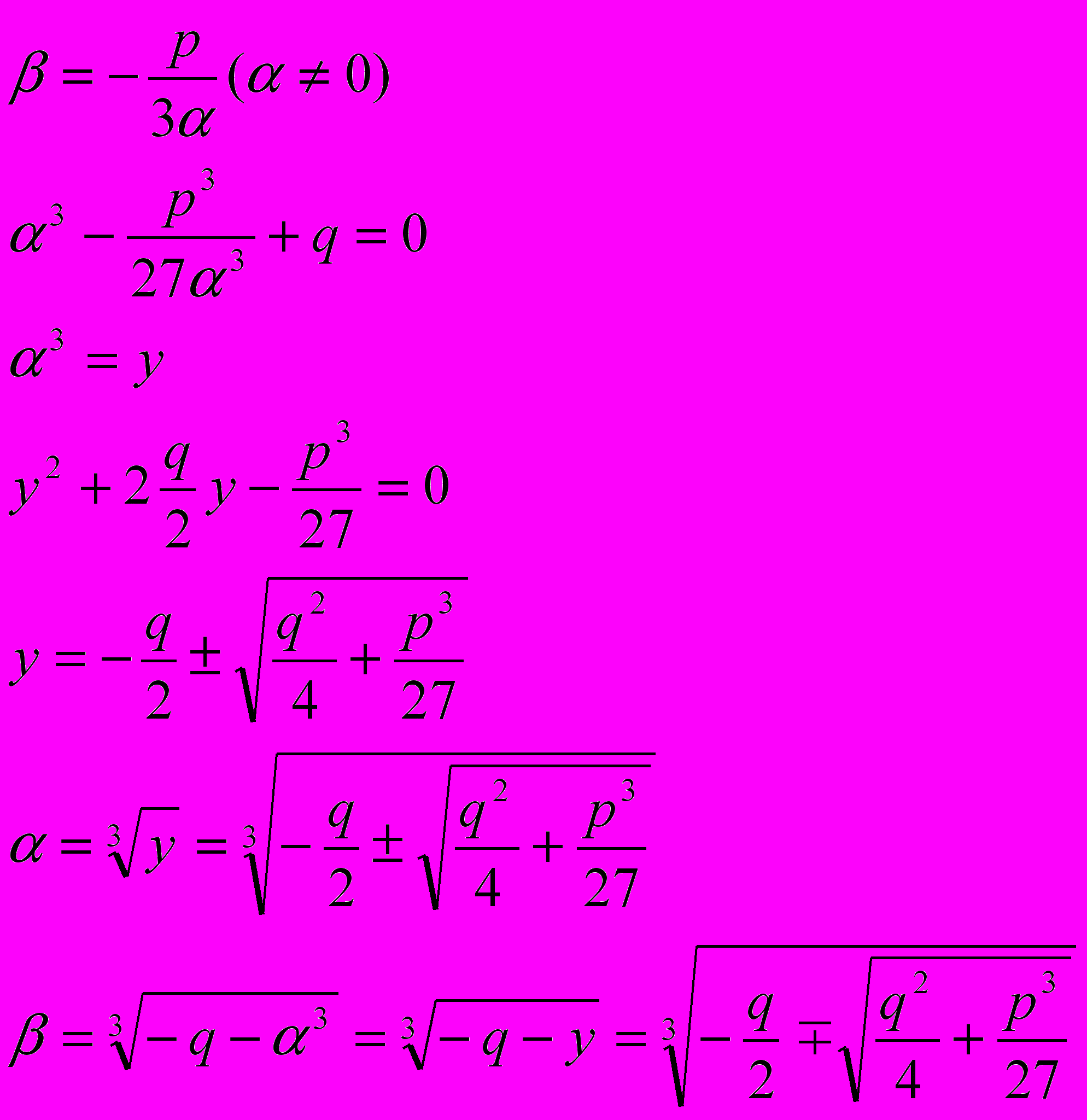
Итак
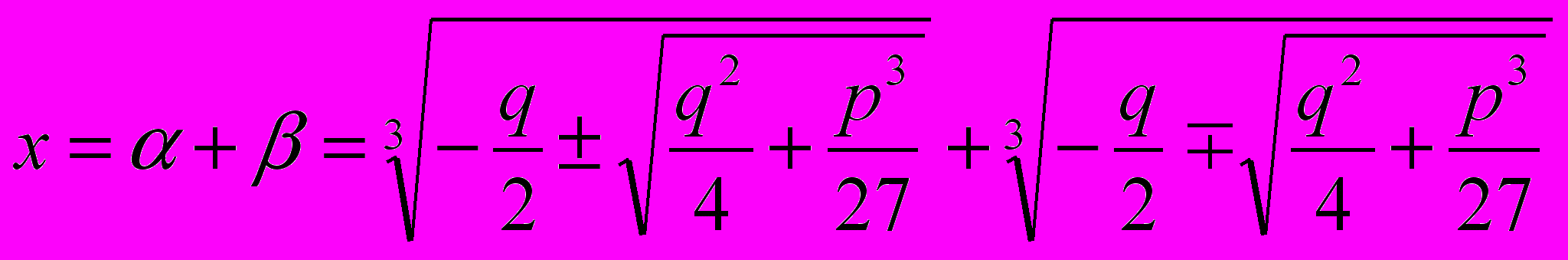
На самом деле ± можно убрать, так как при замене ‘+’ на ‘–‘ просто слагаемые поменяются местами.
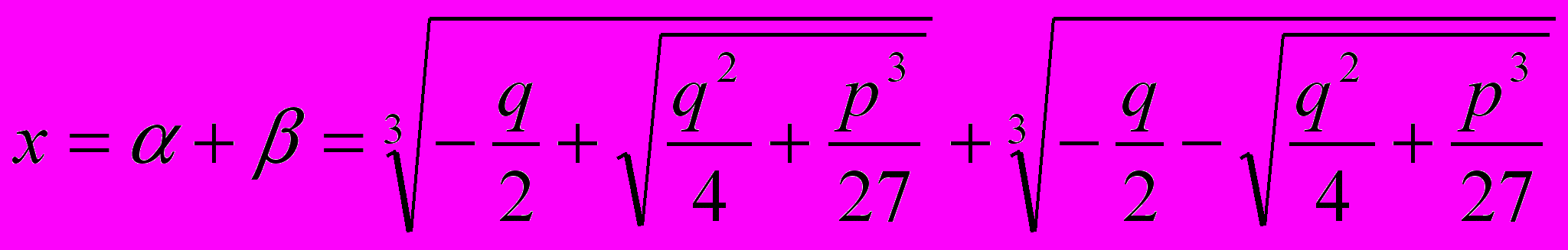
Остальные корни кубического уравнения легко находятся, если известен один из корней уравнения.
Второй вариант решения упрощённого кубического уравнения.
Этот вариант решения делается через тригонометрические функции. Для начала выведем формулу косинуса тройного угла.
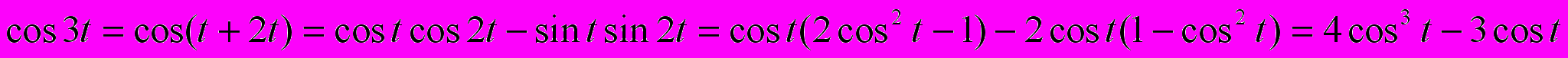В дальнейшем будем считать, что 
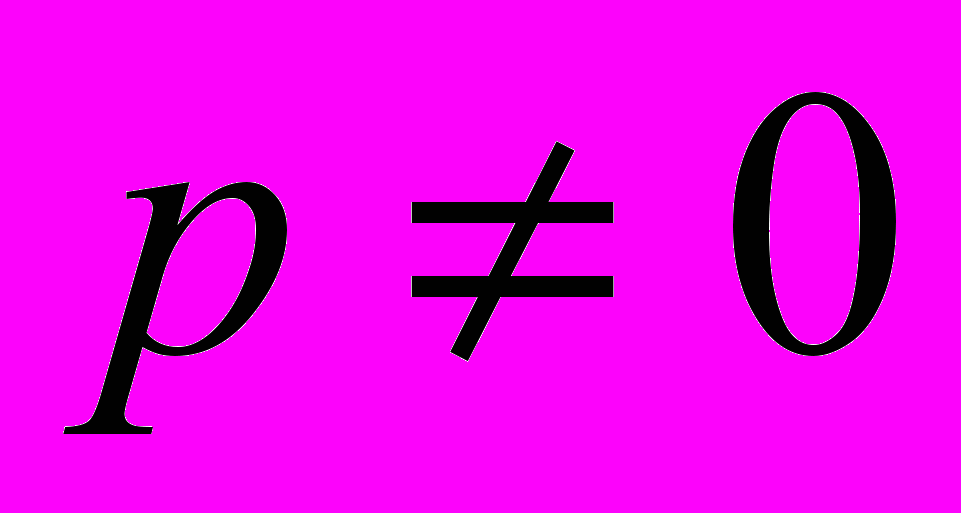. Теперь делая замену 
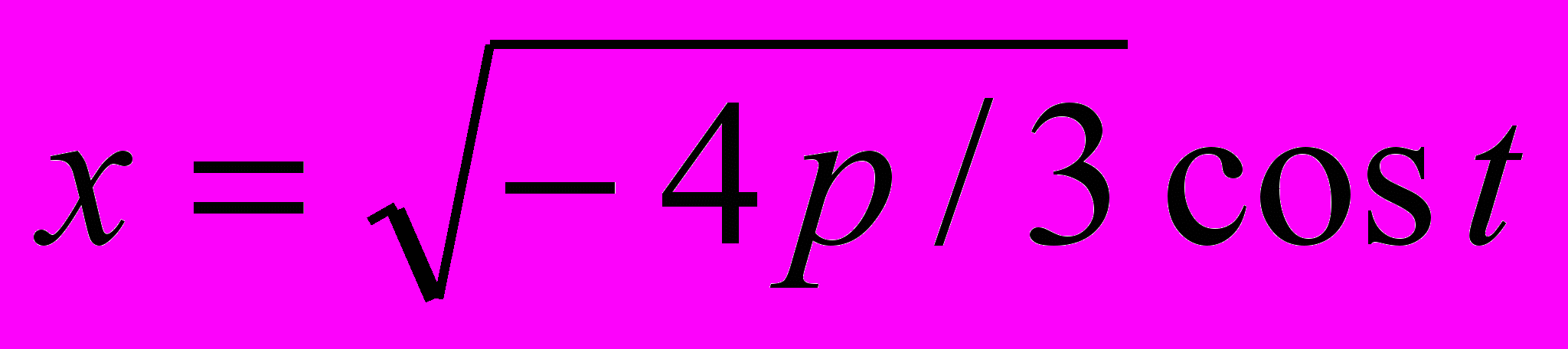, получим.
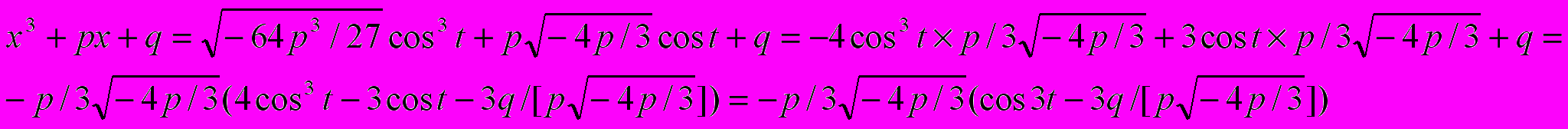Таким образом, используя замену, получаем что 
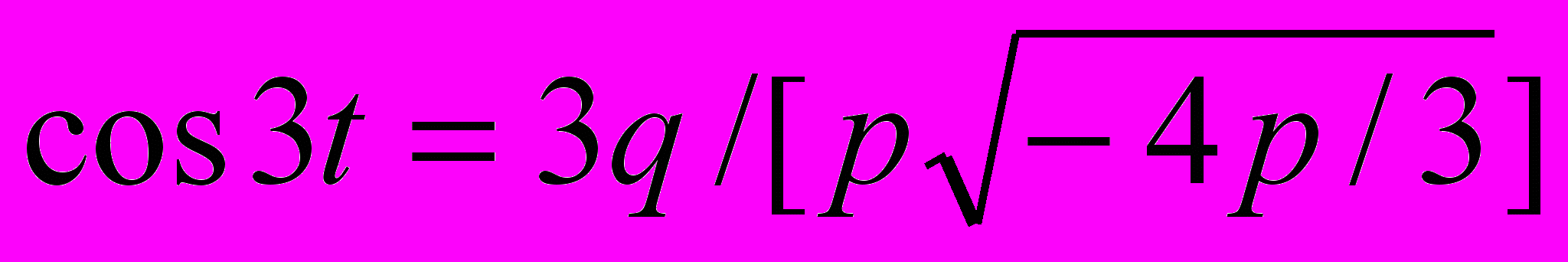, отсюда
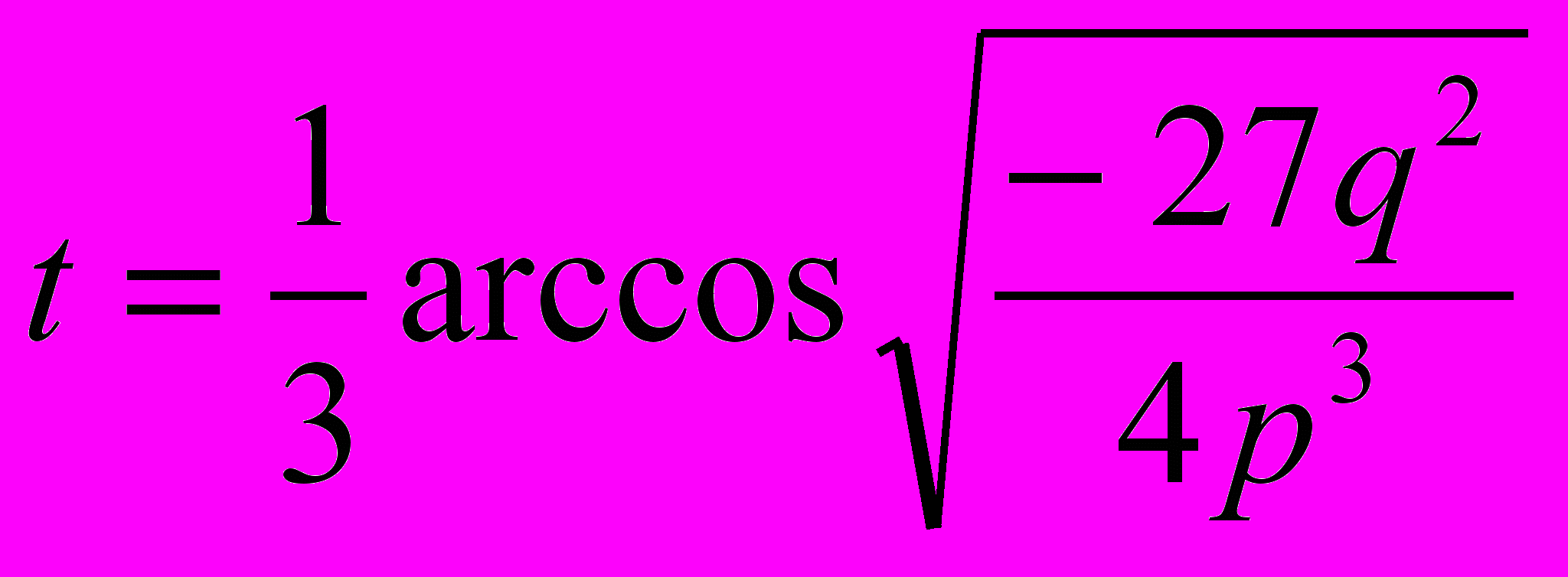, а теперь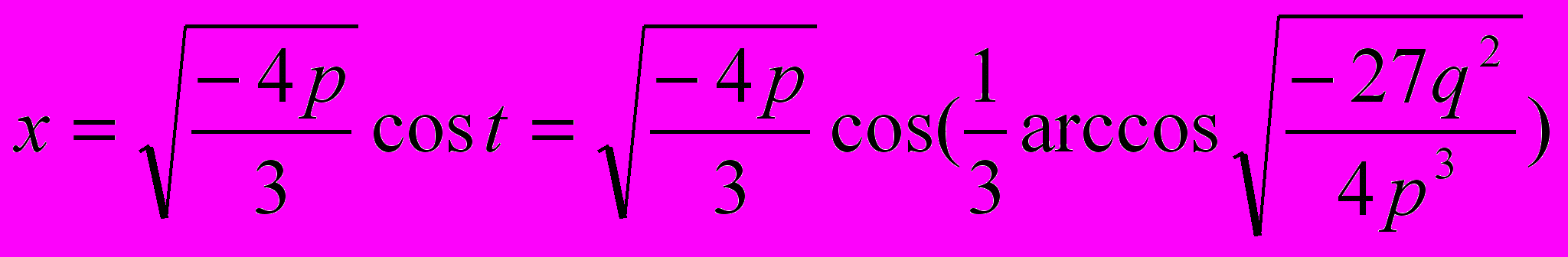 
Иногда выражение стоящее под арккосинусом буде по модулю больше единицы, тогда надо переходить к комплексным числам.
Пример.
Рассмотрим уравнение
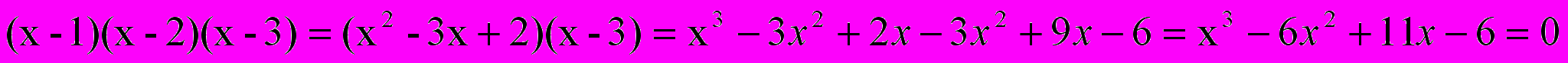
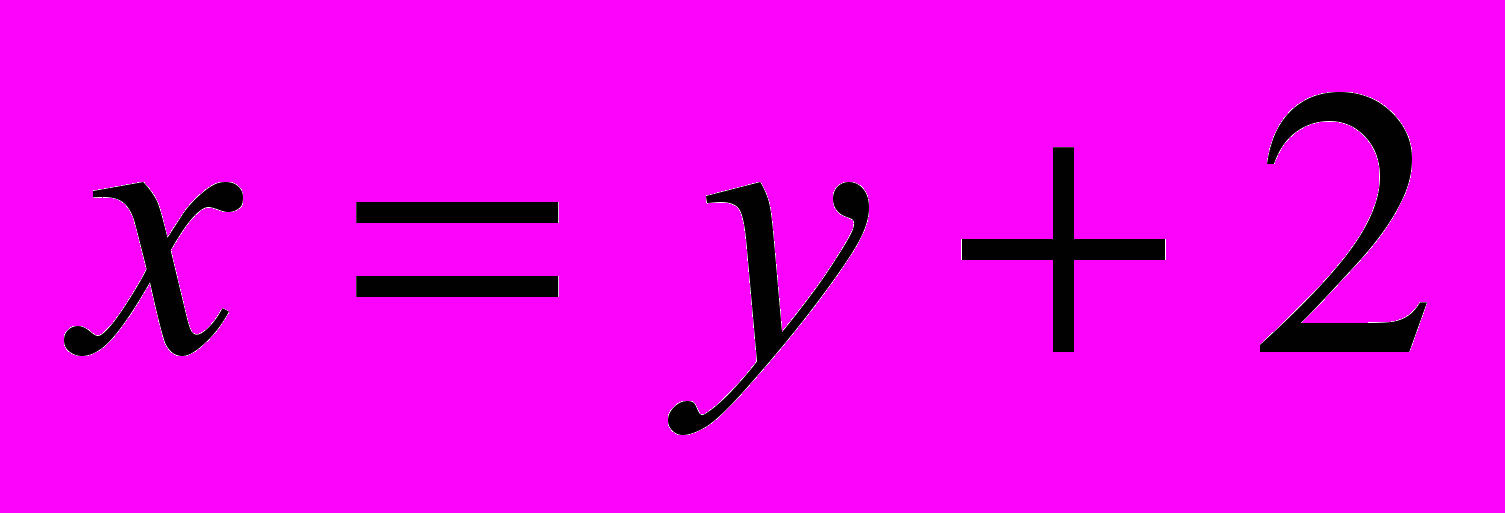
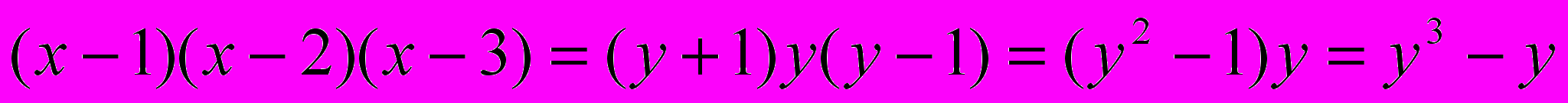
Рассмотрим уравнение
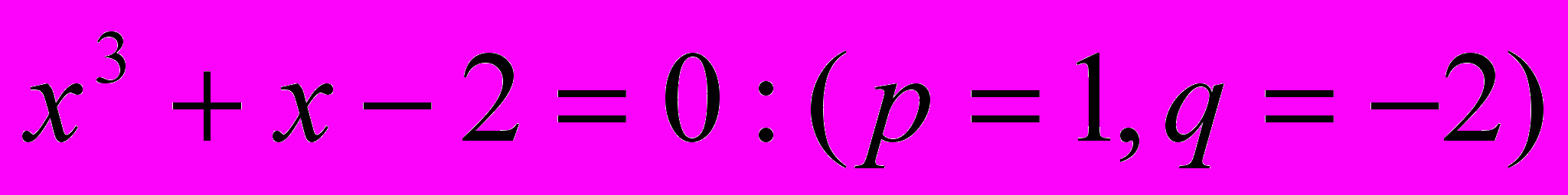(одно из решений 1)