П. В. Чулков, «Уравнения и неравенства в школьном курсе математики, лекции 1-4», стр
| Вид материала | Лекции |
- Владимирова Наталья Анатольевна Студентка 23 группы уравнения и неравенства в школьном, 176.4kb.
- Пояснительная записка Понятие параметра является математическим понятием, которое часто, 163.9kb.
- Методика обучения решению прикладных задач в школьном курсе математики примерное содержание, 14.61kb.
- Методика изучения темы: «Элементы статистики, комбинаторики и теории вероятностей, 1031.61kb.
- Элективный курс по математике для учащихся 9 класса тема: «уравнения и неравенства,, 248.15kb.
- Поурочное планирование (5 часов в неделю, всего 170 часов) Тема, 155.46kb.
- Методика математики 5-6 классов и алгебры 7-9 классов (34ч) Занятие Изучение натуральных, 180.88kb.
- Методика классификации и решения задач с параметрами в курсе средней школы. Уравнения, 18.27kb.
- План внутривузовских изданий митхт им. М. В. Ломоносова на 2007 год., 1434.53kb.
- Урок математики с информатикой по теме «Иррациональные уравнения и неравенства», 43.05kb.
Приложение № 2
( П. В. Чулков, «Уравнения и неравенства в школьном курсе математики, лекции 1-4», стр. 69-70)
Три решения одного уравнения
Решение 1. Возведем обе части уравнения в квадрат и преобразуем полученное уравнение:
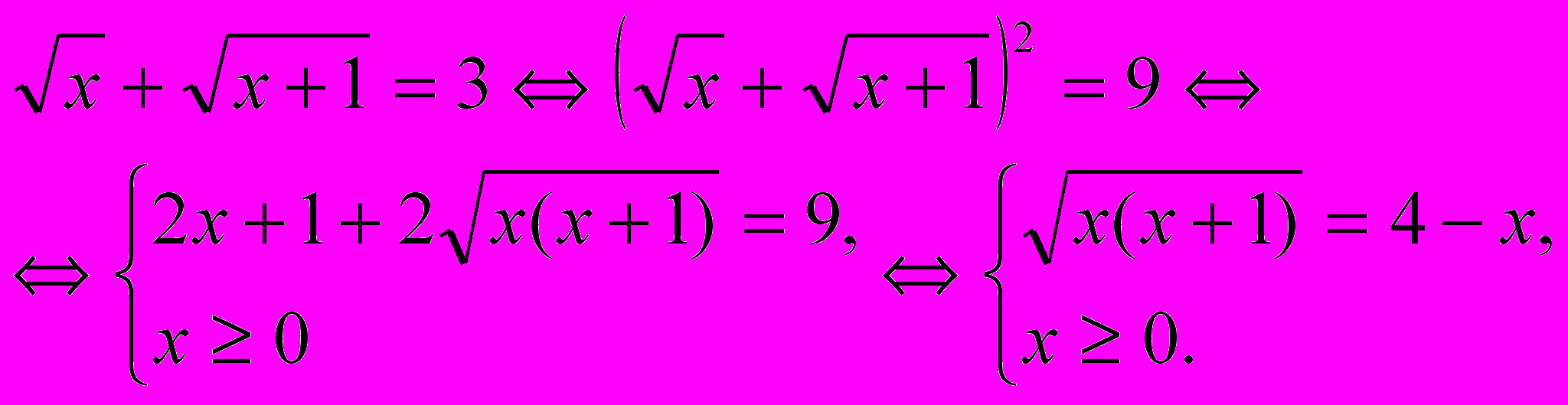
Вновь возведем обе части уравнения в квадрат:
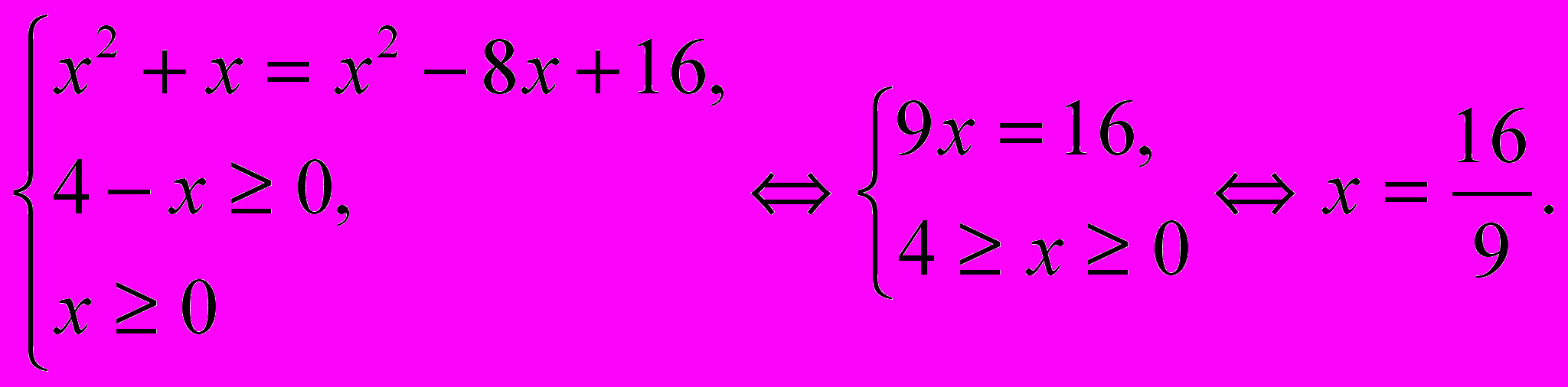
Ответ:
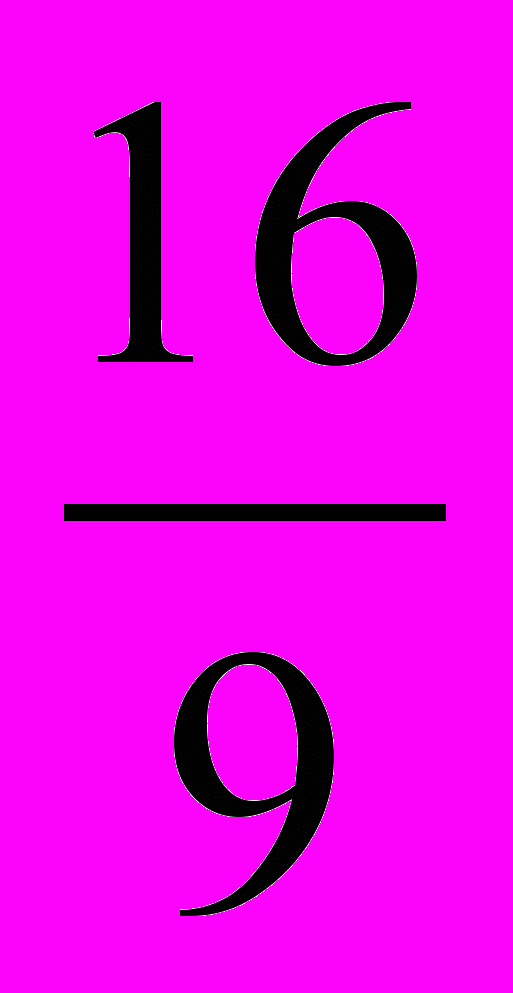.Решение 2. Пусть
, 
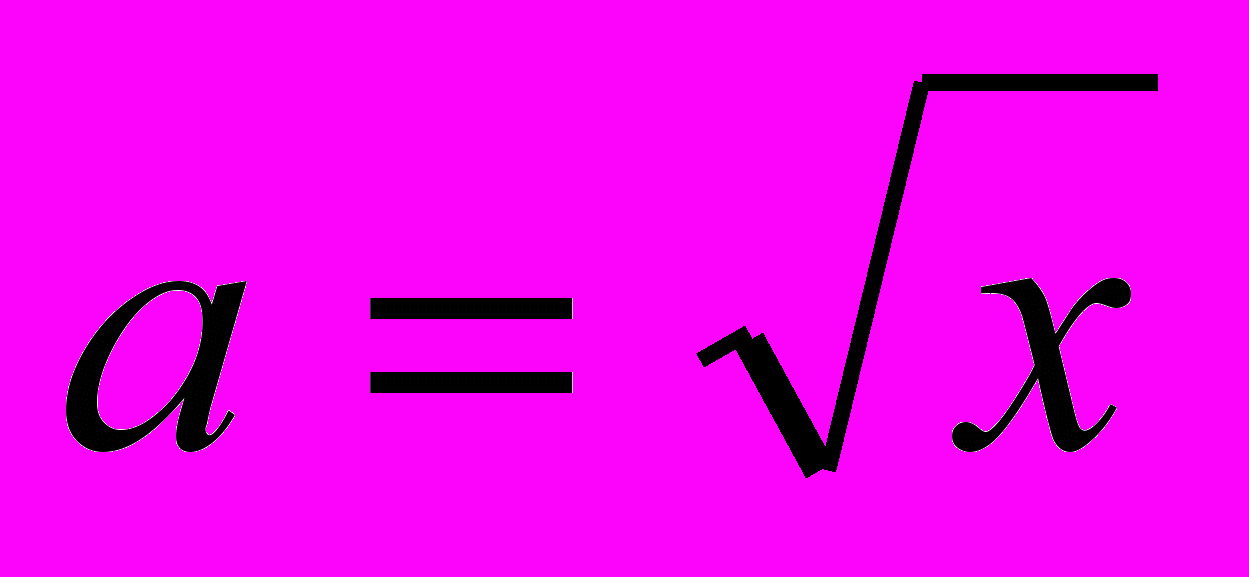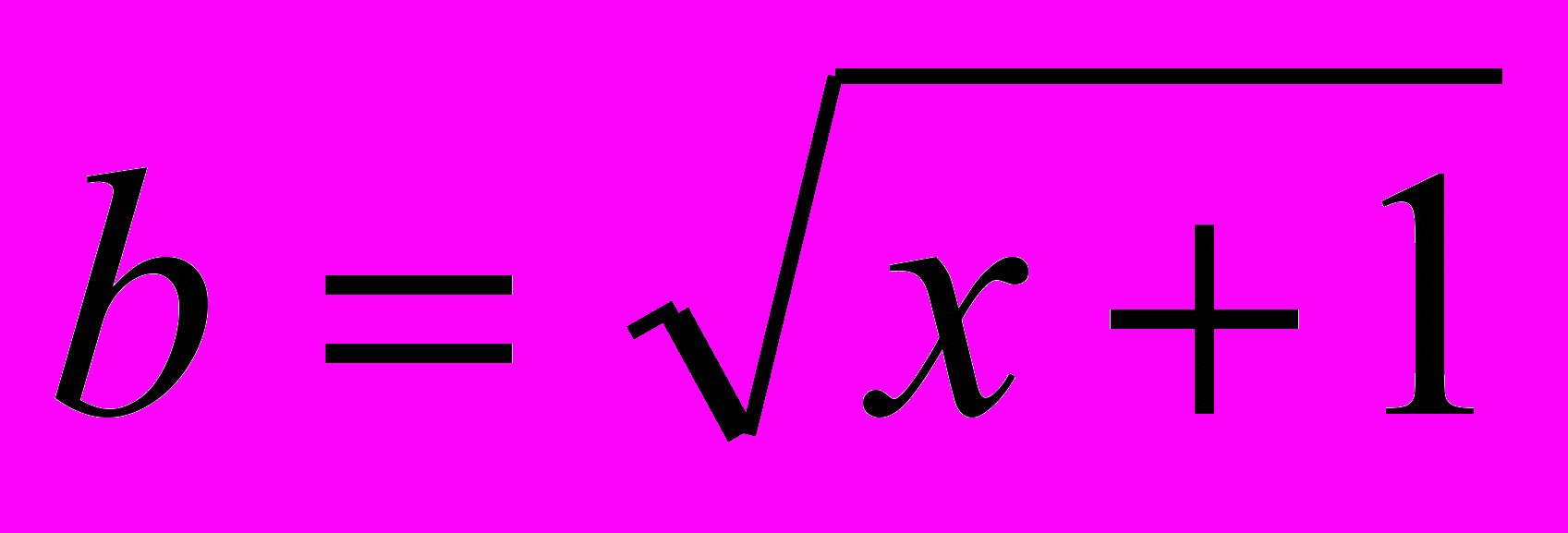.Получим систему:
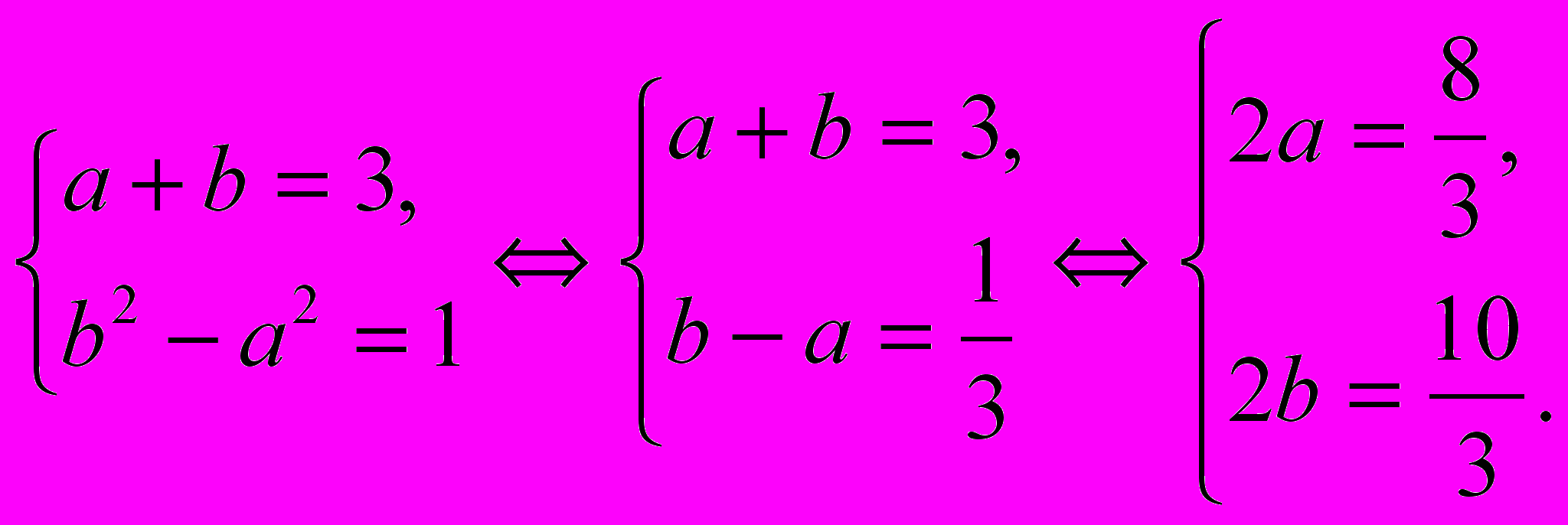
Следовательно,
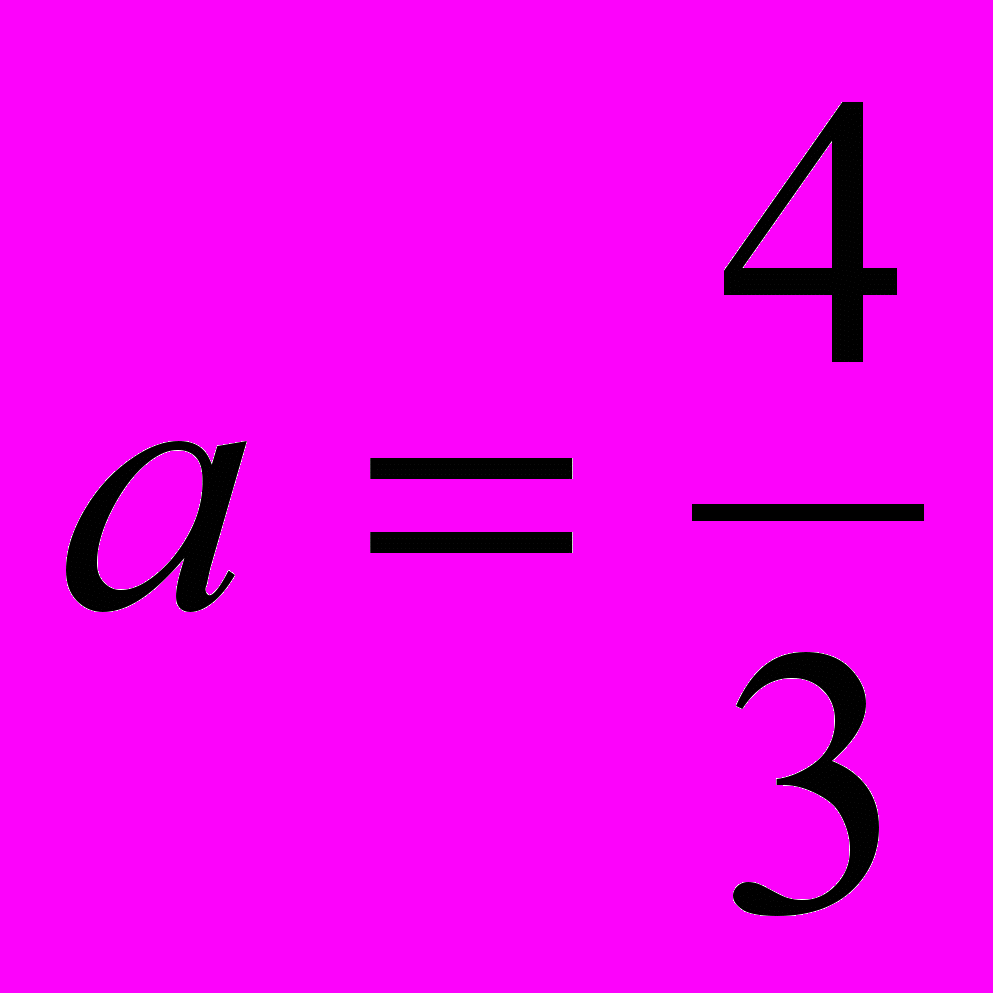, откуда 
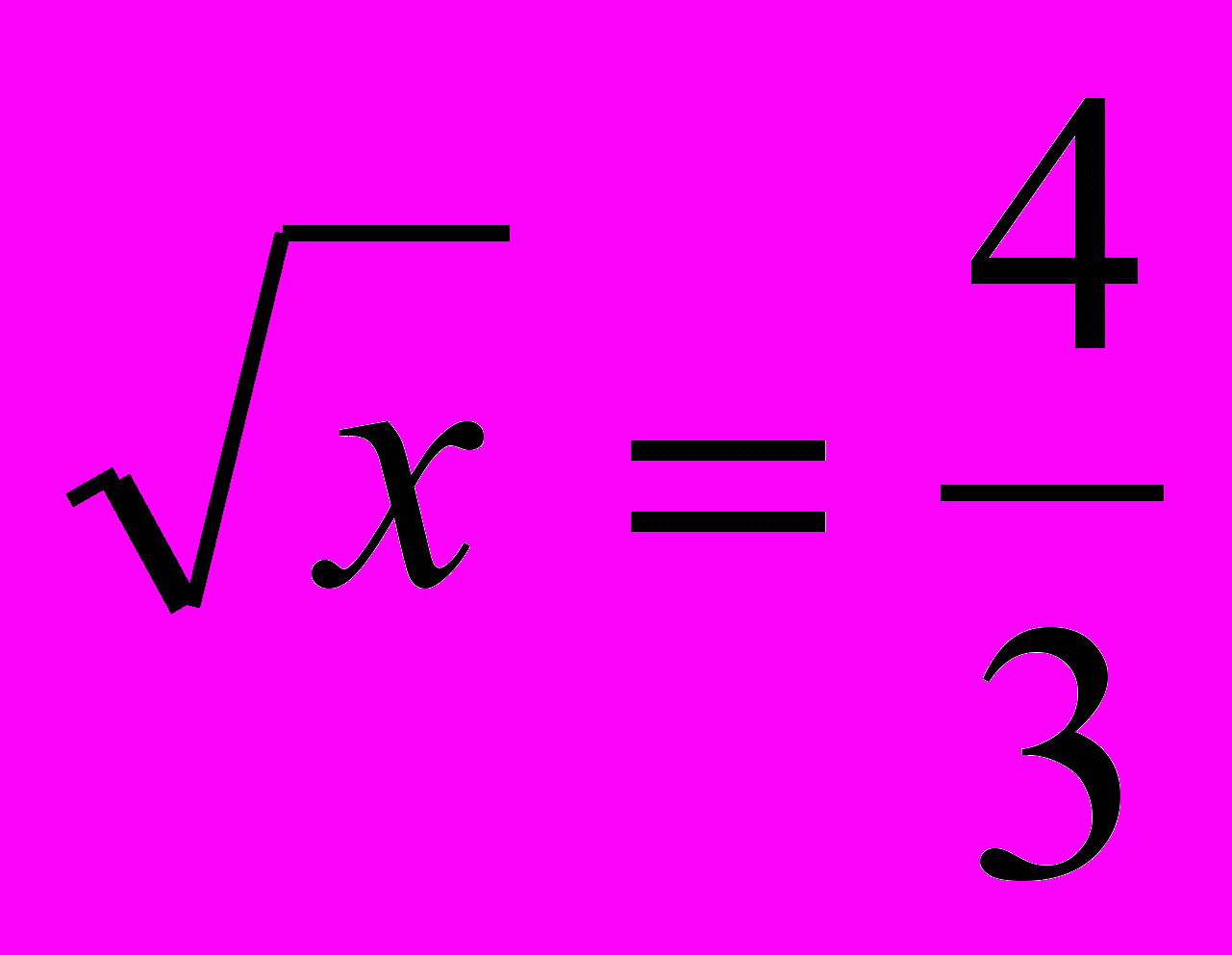и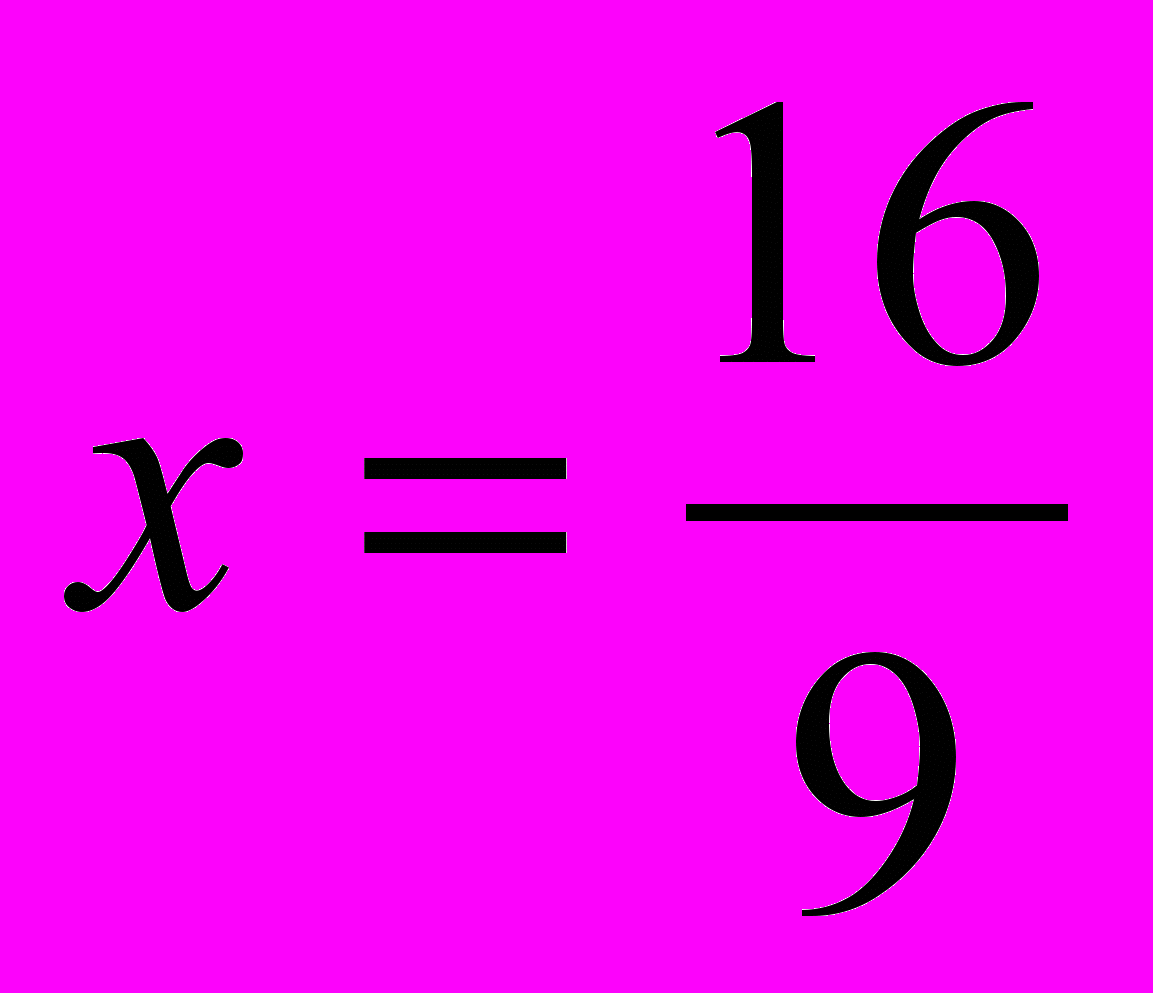 
.Проверка показывает, что
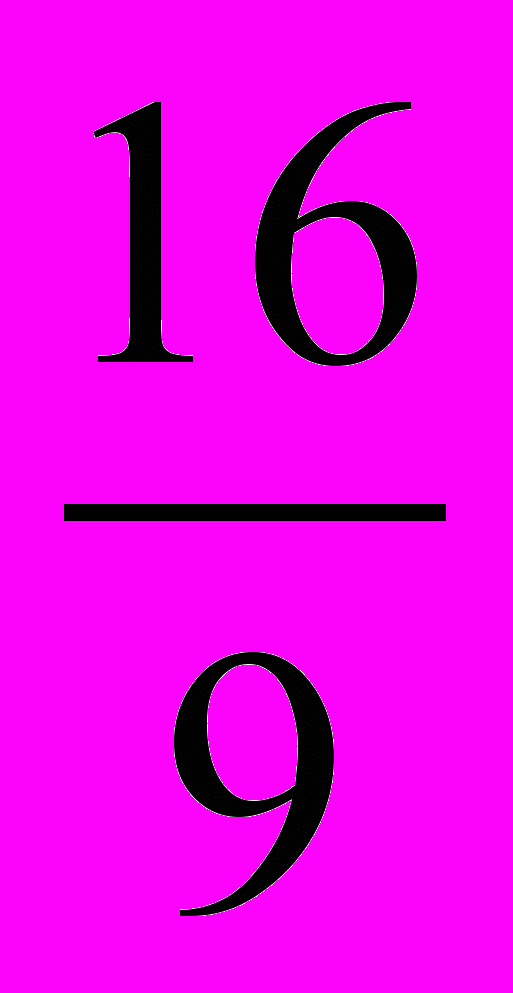- корень исходного уравнения.Решение 3. Пусть
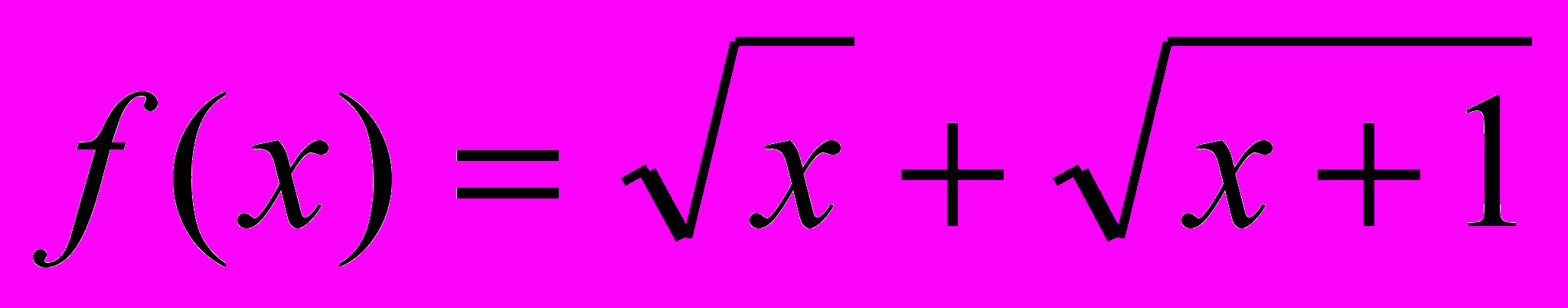.Заметим, что
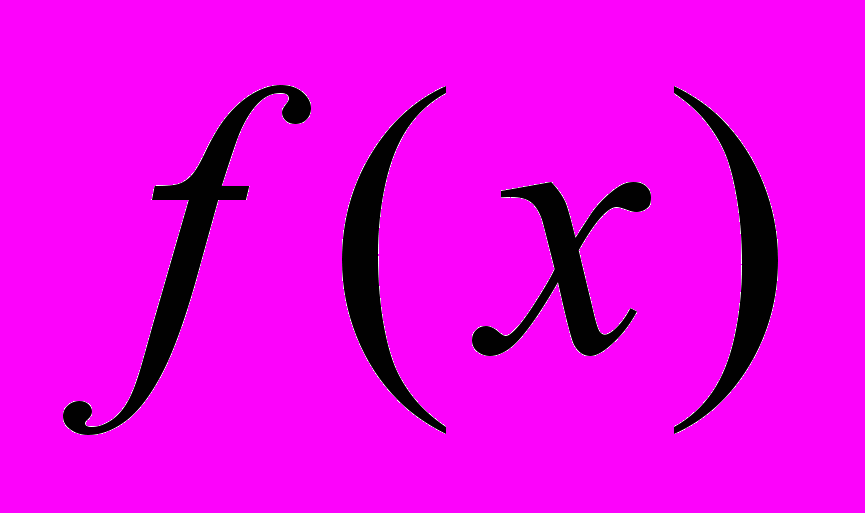- возрастающая функция на своей области определения.Из курса алгебры и начал анализа известно, что возрастающая функция принимает каждое из своих значений только при одном значении аргумента, а следовательно, имеет не более одного корня:
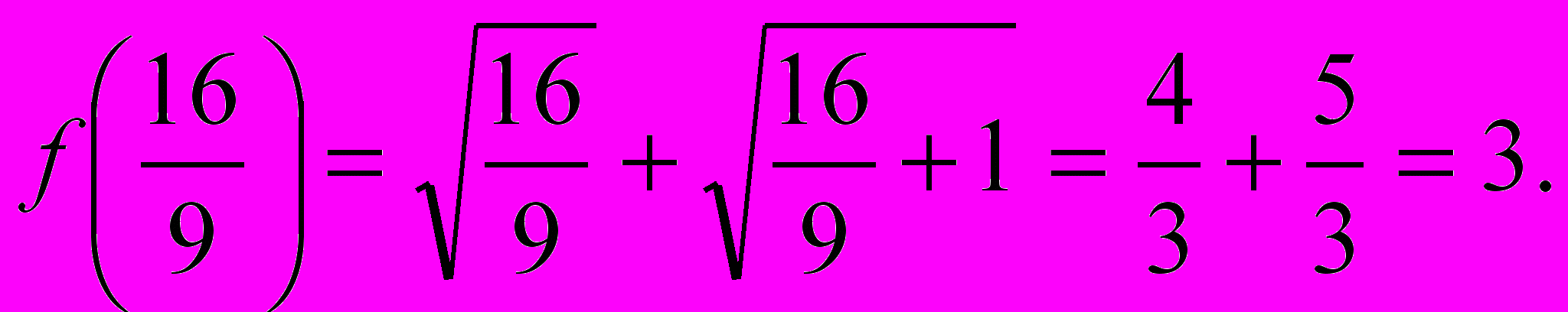
Следовательно,
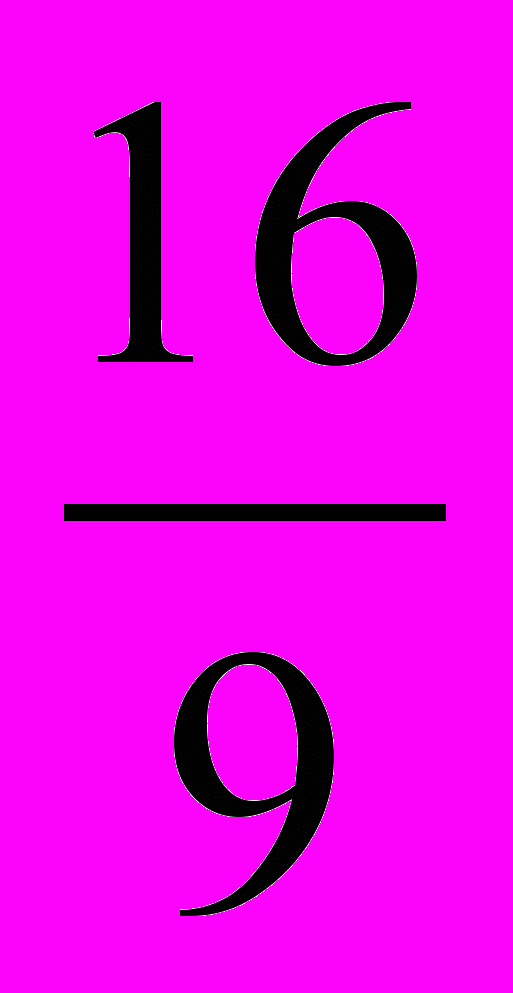- единственный корень исходного уравнения.