Владимирова Наталья Анатольевна Студентка 23 группы уравнения и неравенства в школьном курсе математики реферат

Вид материала

Содержание

1. Понятие уравнения
2. Решение уравнений, содержащих переменную под знаком модуля
4. Иррациональные уравнения
4.1 Решение иррациональных уравнений стандартного вида
5. Иррациональные неравенства
5.1 Решение иррациональных неравенств стандартного вида
6. Квадратные уравнения и уравнения, сводящиеся к ним
6.1 Теорема Виета
Список используемой литературы

Подобный материал:

УПРАВЛЕНИЕ ОБРАЗОВАНИЯ И НАУКИ БЕЛГОРОДСКОЙ ОБЛАСТИ

Валуйский педагогический колледж

Школьное отделение

Предметно-цикловая комиссия физики, математики и информатики

Владимирова Наталья Анатольевна

Студентка 23 группы

УРАВНЕНИЯ И НЕРАВЕНСТВА В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ

Реферат по методике преподавания математики

Научный руководитель:

Старокожева Е. И.

Валуйки, 2007

Оглавление

Введение……………………………………………………………….……. 3

Понятие уравнения…………………………………………………….... 5
Решение уравнений содержащих переменную под знаком модуля……………………………………………………………………..5

Иррациональные уравнения……………………………..……………..10
1. Решение иррациональных уравнений стандартного вида………...10
2. Иррациональные уравнения, которые решаются заменой………..12
Иррациональные неравенства……………………………………..…...14
1. Решение иррациональных неравенств стандартного вида…..……14
Квадратные уравнения и уравнения, сводящиеся к ним……………..16

6.1 Теорема Виета………………………………………………………..…18

Заключение………………………………………………………………….21

8.Список используемой литературы……………………………………...22

Введение

Истоки алгебраических методов решения практических задач связан с
наукой древнего мира. Как известно из истории математики, значительная часть задач математического характера, решаемых египетскими, шумерскими, вавилонскими писцами-вычислителями (XX—VI вв. до н. э.), имела расчетный характер. Однако уже тогда время от времени возникали задачи, в которых искомое значение величины задавалось некоторыми косвенными условиями, требующими, с нашей современной точки зрения, составления уравнения или системы уравнений. Первоначально для решения таких задач применялись арифметические методы. В дальнейшем начали формироваться начатки алгебраических представлений. Например, вавилонские вычислители умели решать задачи, сводящиеся с точки зрения современной классификации к уравнениям второй степени. Таким образом, был создан метод решения текстовых задач, послуживший в дальнейшем основой для выделения алгебраического компонента и его независимого изучения.
Это изучение осуществлялось уже в другую эпоху сначала арабскими
математиками (VI—Х вв. н. э.), выделившими характерные действия,
посредством которых уравнения приводились к стандартному виду
(приведение подобных членов, перенос членов из одной части уравнения в другую с переменой знака), а затем европейскими математиками Возрождения, в итоге длительного поиска создавшими язык современной алгебры (использование букв, введение символов арифметических операций, скобок и т. д.). На рубеже XVI—XVII вв. алгебра как специфическая часть математики, обладающая своим предметом, методом, областями приложения, была уже сформирована. Дальнейшее ее развитие, вплоть до нашего времени, состояло в совершенствовании методов, расширении области приложений, уточнении понятий и связей их с понятиями других разделов математики. В этом процессе все яснее становилась важность роли, которую играло понятие уравнения в
системе алгебраических понятий.

Открытие координатного метода (Декарт, XVII в.) и последовавшее за
ним развитие аналитической геометрии позволили применить алгебру не только к задачам, связанным с числовой системой, но и к изучению различных геометрических фигур. Эта линия развития алгебры упрочила положение уравнения как ведущего алгебраического понятия, которое связывалось теперь уже с тремя главными областями своего возникновения и функционирования:
a) уравнение как средство решения текстовых задач;
b) уравнение как особого рода формула, служащая в алгебре объектом изучения;
c) уравнение как формула, которой косвенно определяются числа или
координаты точек плоскости (пространства), служащие его решением.
Каждое из этих представлений оказалось в том или ином отношении
полезным.

Таким образом, уравнение как общематематическое понятие много аспектное, причем ни один из аспектов нельзя исключить из рассмотрения, особенно если речь идет о проблемах школьного математического образования.

1. Понятие уравнения

Понятие уравнения относится к важнейшим общематематическим понятиям. Именно поэтому затруднительно предложить его определение, одновременно и строгое с формальной точки зрения, и доступное для учащихся, приступающих к овладению школьным курсом алгебры.
Материал, связанный с уравнениями, составляет значительную часть
школьного курса математики. Это объясняется тем, что уравнения широко используются в различных разделах математики, в решении важных прикладных задач.
Ввиду важности и обширности материала, связанного с понятием уравнения, его изучение в современной методике математики организовано в содержательно - методическую линию — линию уравнений и неравенств. Здесь рассматриваются вопросы формирования понятий уравнения и неравенства, общих и частных методов их решения, взаимосвязи изучения уравнений и неравенств с числовой, функциональной и другими линиями школьного курса математики.

2. Решение уравнений, содержащих переменную под знаком модуля

Уравнения, содержащие переменную под знаком модуля, могут решаться несколькими способами. Способ выбирается в зависимости от вида уравнения. Основные способы: метод отрезков, возведение в квадрат, могут применяться и нестандартные способы. При решении уравнений может одновременно использоваться несколько способов.

1. Возведением в квадрат

|2х-5|=х

возведем в квадрат это уравнение:

(|2х-5|)²=(x)²

4х²-20х+25=х²

3х²-20х+25=0

D=k²-ac= (-10)²-3∙25=100-75=25 D>0

Возведение в четную не является равносильным преобразованием, т.к.

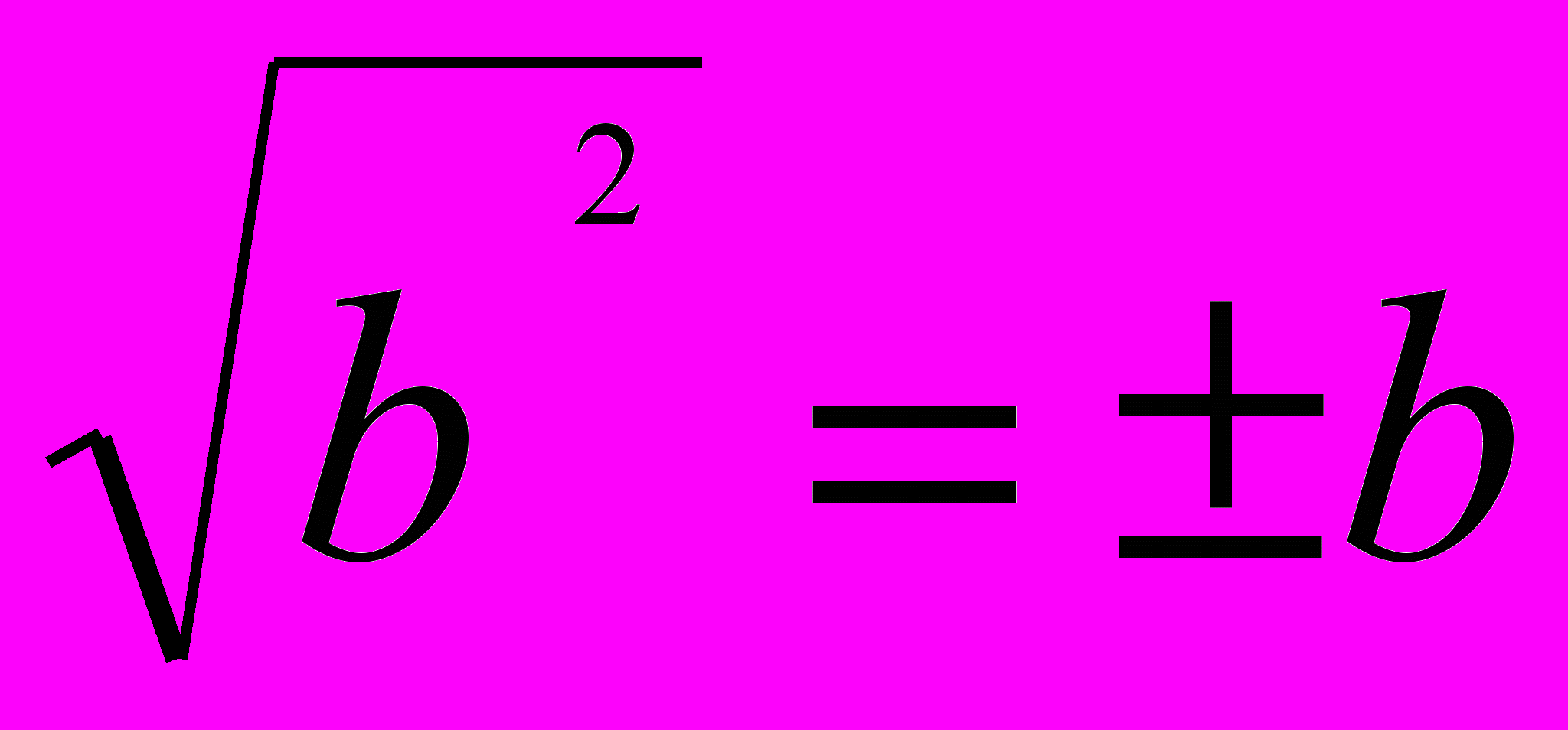, ОДЗ не задавалось, поэтому произведем проверку.

Проверка.

Для х₁:

верно

Для х₂

|2∙5-5|=5

|10-5|=5

|5|=5

5=5

верно

2. методом отрезков:

а) |2х +3|=|х-2|

2х +3=0 → x = -1,5

х-2=0 → x=2

Третий корень является посторонним, т. к. все преобразования были равносильными то проверка не нужна.

Ответ:

б)x+ | x -1|=1

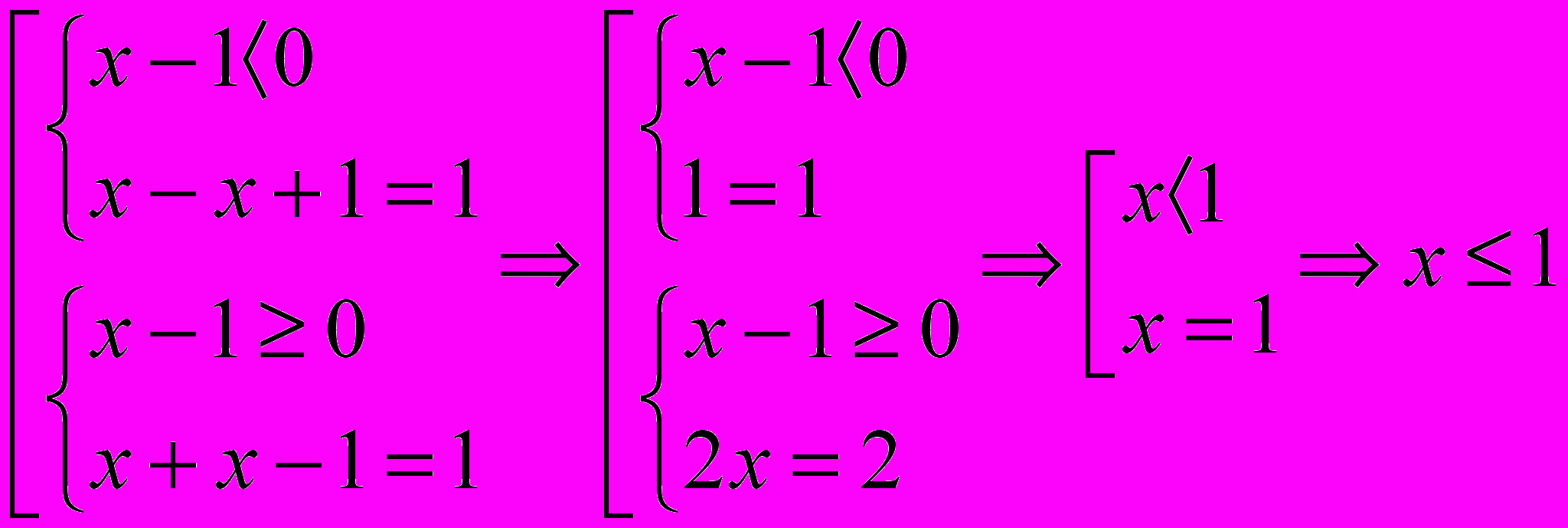
Ответ:

3. Иногда применяется несколько методов одновременно.

Например.

||x|+5|=6

Возведем уравнение в квадрат.

(|x|+5)²=36

х²+10|x|+25=36

Применим метод отрезков.

x²+10x-11=0

D=k2-ac=25+11=36 D>0

x₁=-5+6=1

x₂=-5-6=-11

x²-10x-11=0

D=k2-ac=25+11=36 D>0

x₃=5+6=11

х₄=5-6=-1

Проверка.

Для x₁:

||1|+5|=6

6=6 верно

Для x₄:

||-1|+5|=6

6=6 верно

Ответ: x₁=1, x₄=-1

4. Нестандартным способом.

|x-8|=x-8

Выражения, стоящие в левой и правой части уравнения различаются только знаком модуля, поэтому решением уравнения будет его область определения.

Найдем область определения: так-так левая часть уравнения больше нуля, то и правая часть тоже больше нуля, тогда

х-8≥0 ð х≥8

т. к. х-8>0 то

х-8=х-8

0=0 равенство, верно, значит x ≥8 ,будет решением данного уравнения. Ответ: xÎ(8,+∞)

4. Иррациональные уравнения

Иррациональным называется уравнение, в котором переменная содержится под знаком корня.

Решаются такие уравнения возведением обеих частей в степень. При возведении в четную степень возможно расширение области определения заданного уравнения. Поэтому при решении таких иррациональных уравнений обязательны проверка или нахождение области допустимых значений уравнений. При возведении в нечетную степень обеих частей иррационального уравнения область определения не меняется.

Иррациональные уравнения стандартного вида можно решить, пользуясь следующим правилом:

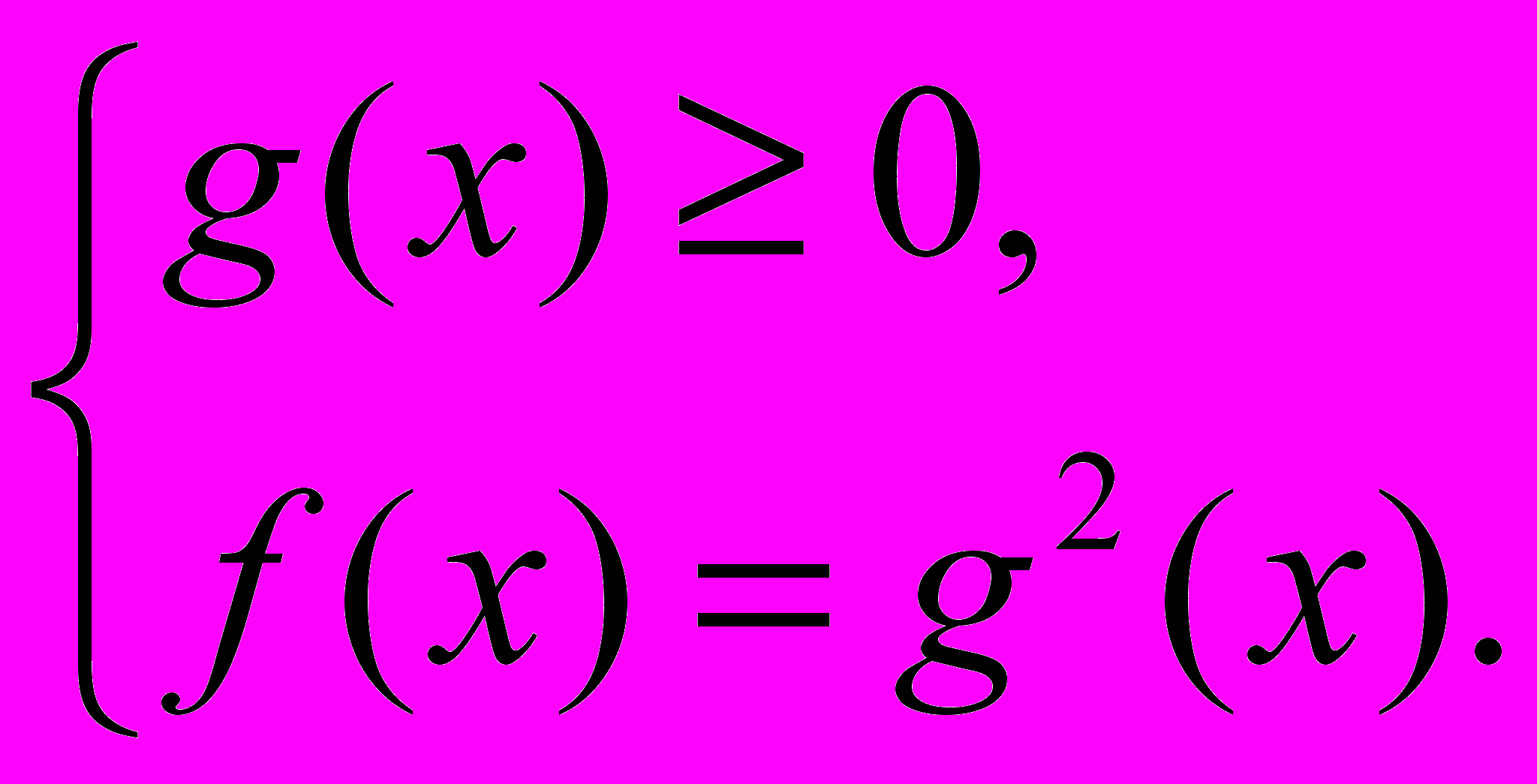
4.1 Решение иррациональных уравнений стандартного вида:

а) Решить уравнение

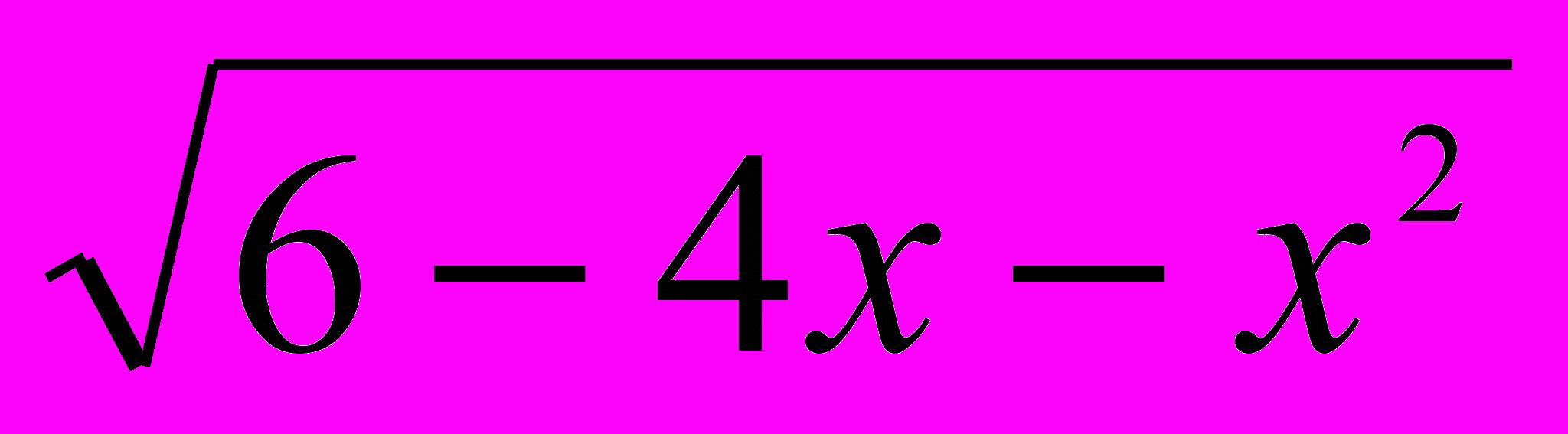= x + 4,

Решение.

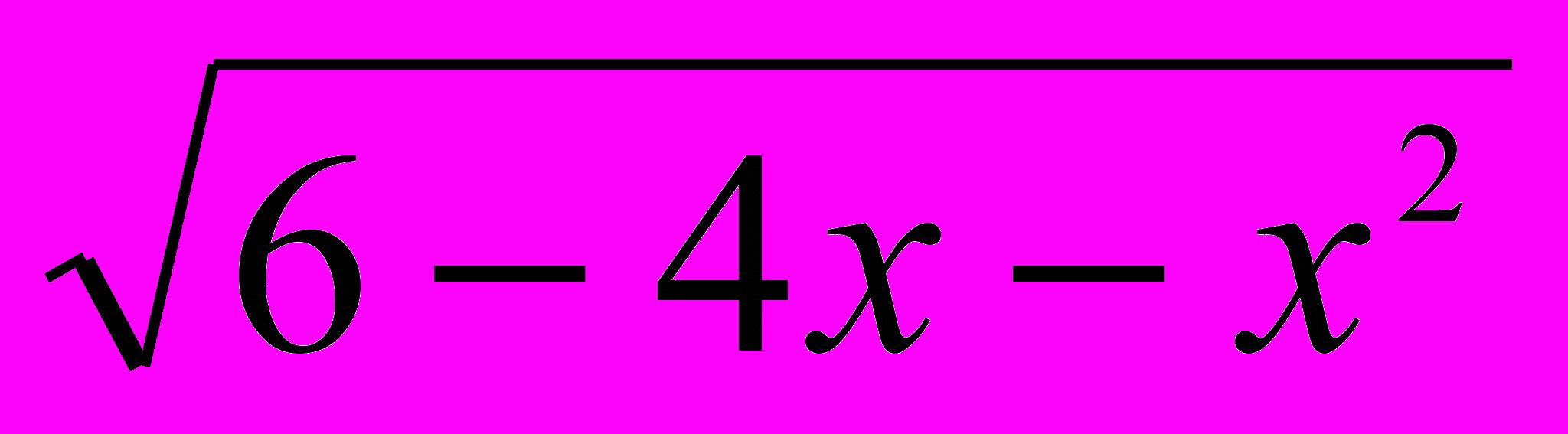= x + 4,

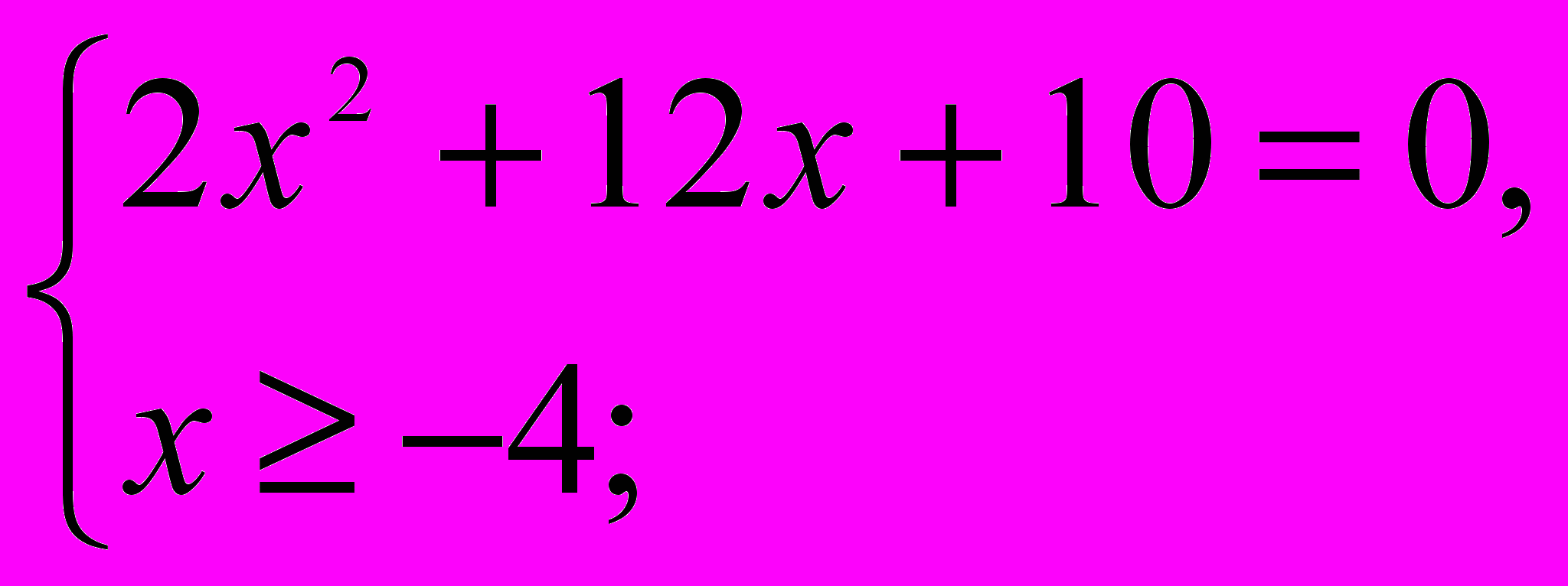
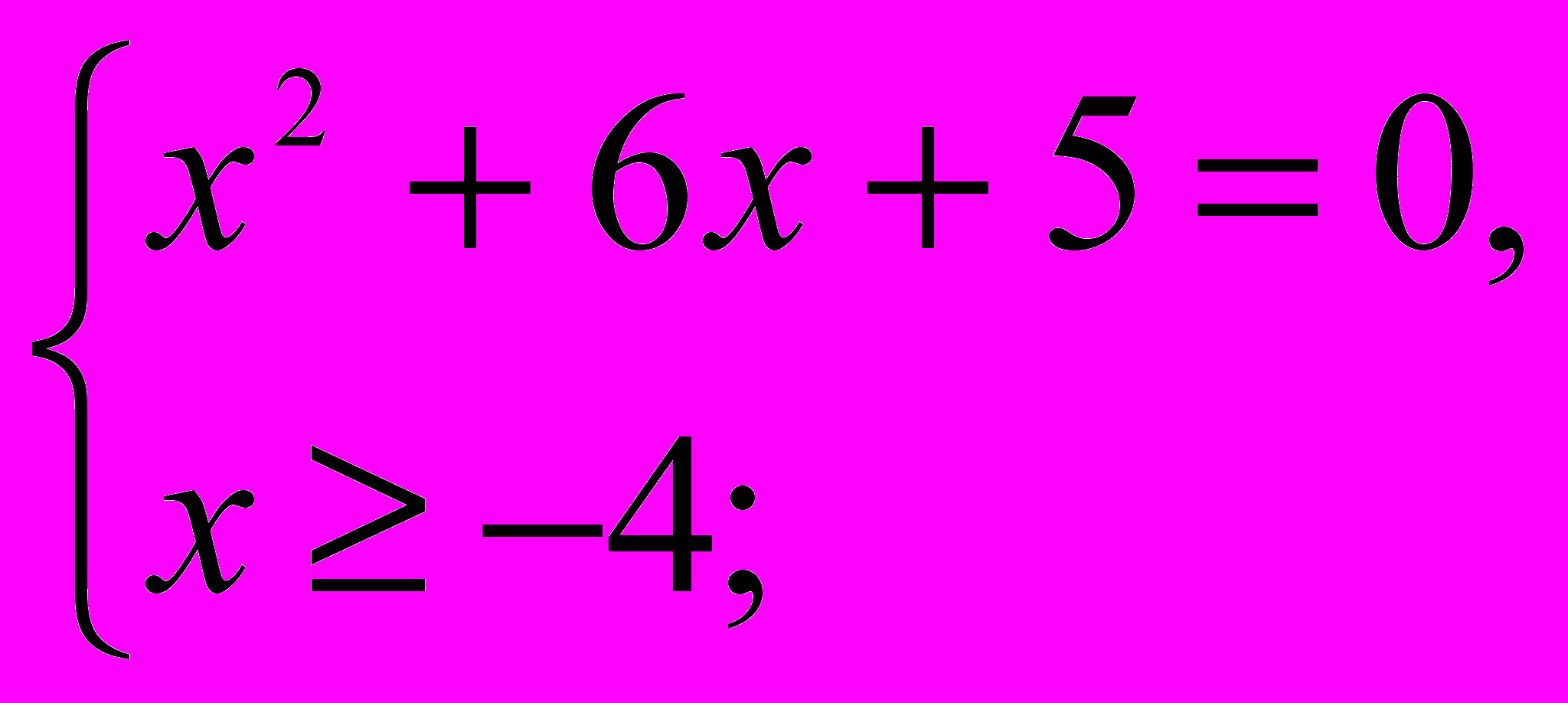
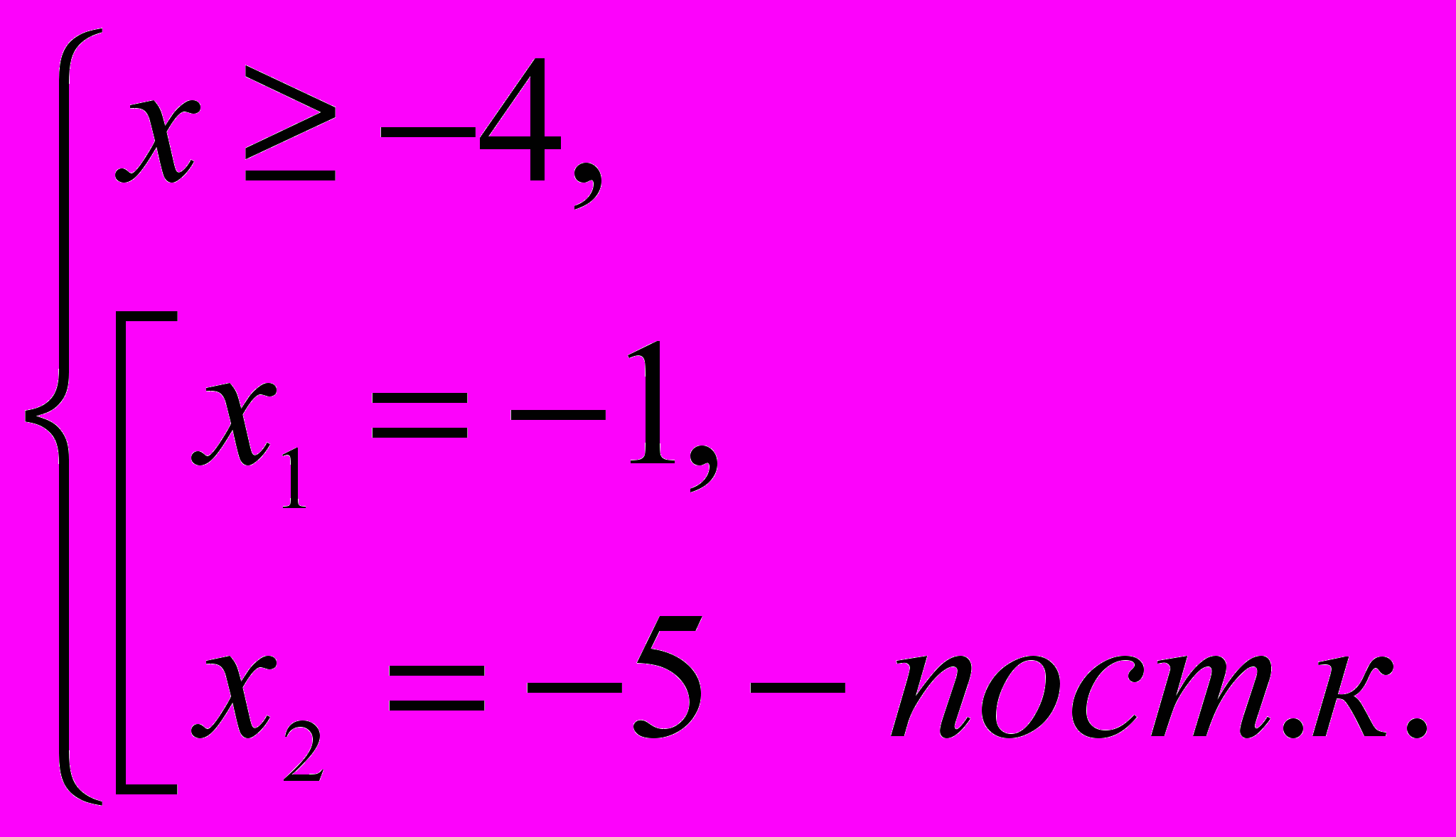
Ответ: -1

б) Решить уравнение x– 1 =

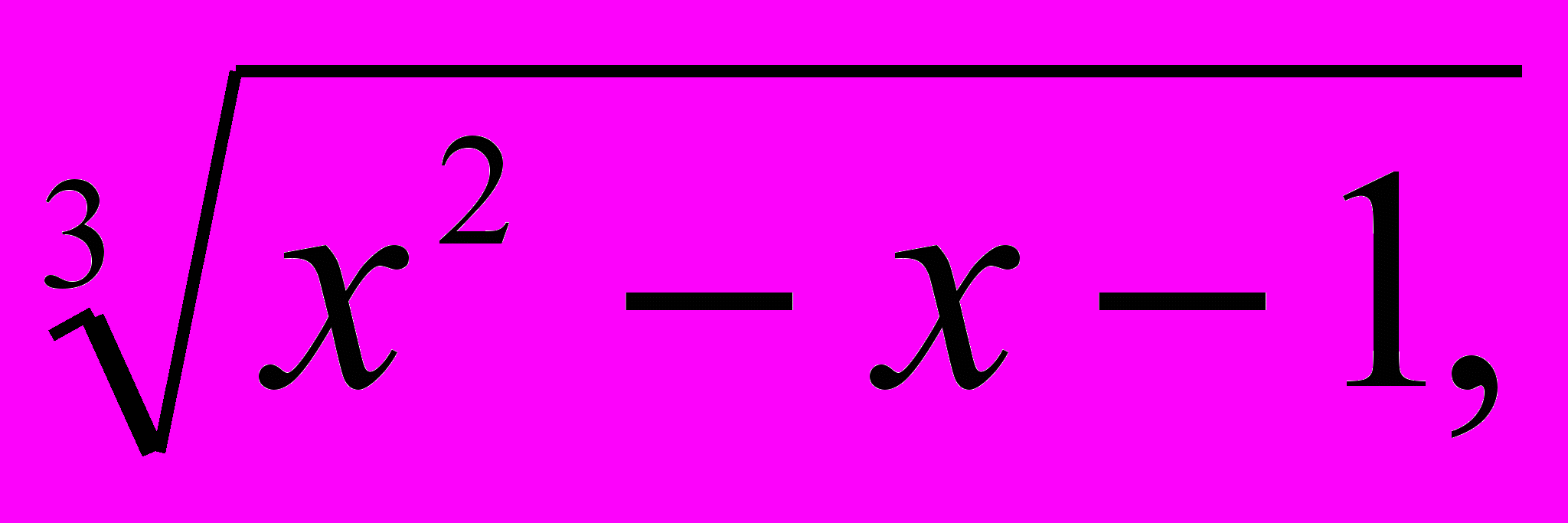
Решение.

x – 1 =

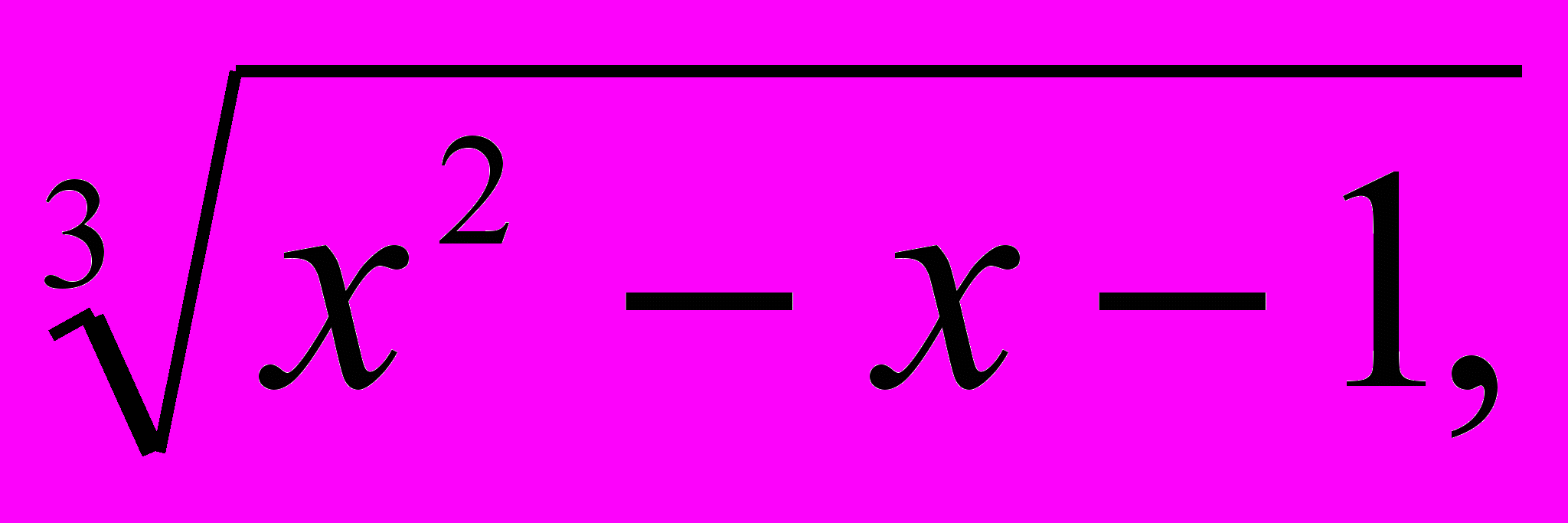
х³ – 3х² + 3х – 1 = х² – x– 1,

х³ – 4х² + 4х = 0,

x (х² – 4х + 4) = 0,

x= 0 или х² – 4х + 4 = 0,

(x – 2)² = 0,

x = 2

Ответ: 0; 2.

в) Решить уравнение

= x – 2,

Решение.

= x – 2,

2x – 1 = x² – 4x + 4, Проверка:

x² – 6x + 5 = 0, x = 5,

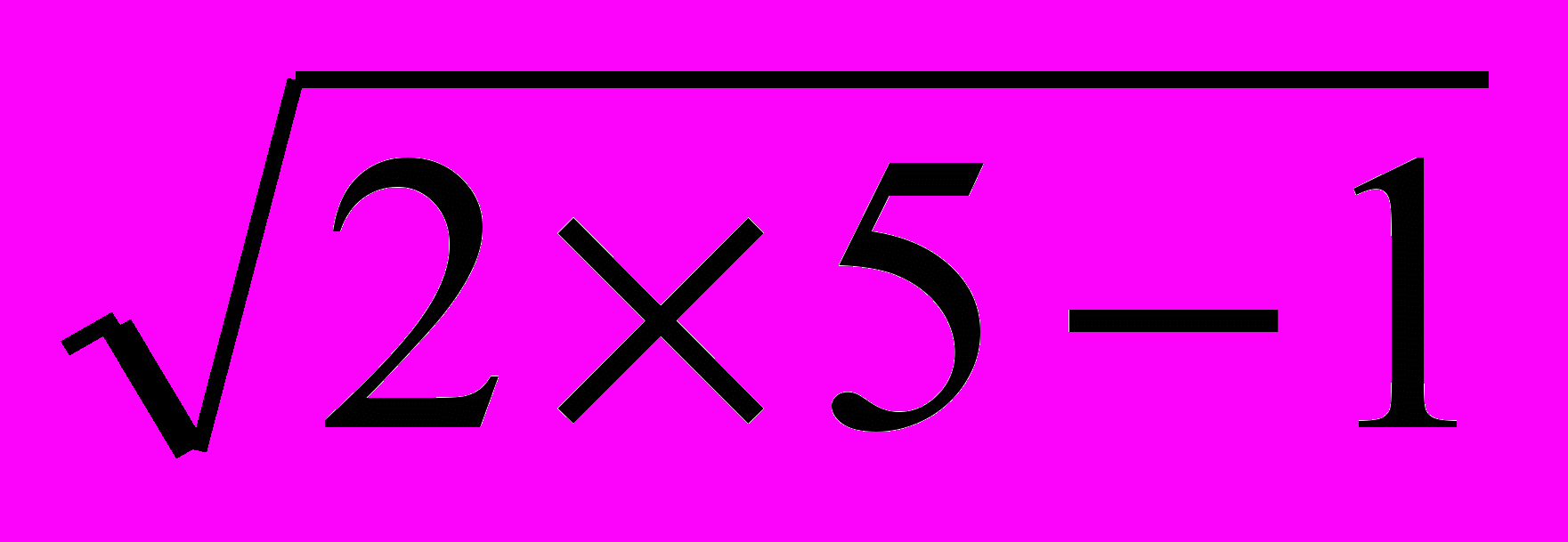= 5 – 2,

x₁ = 5, 3 = 3

x₂ = 1 – посторонний корень x = 1,

1 – 2,

Ответ: 5 пост, к. 1

-1.

г) Решить уравнение x –

+ 4 = 0,

Решение.

x –

+ 4 = 0,

x + 4 =

, Проверка:

х² + 8х + 16 = 25х – 50, x = 11, 11 –

+ 4 = 0,

х² – 17х + 66 = 0, 0 = 0

х₁ = 11, x = 6, 6 –

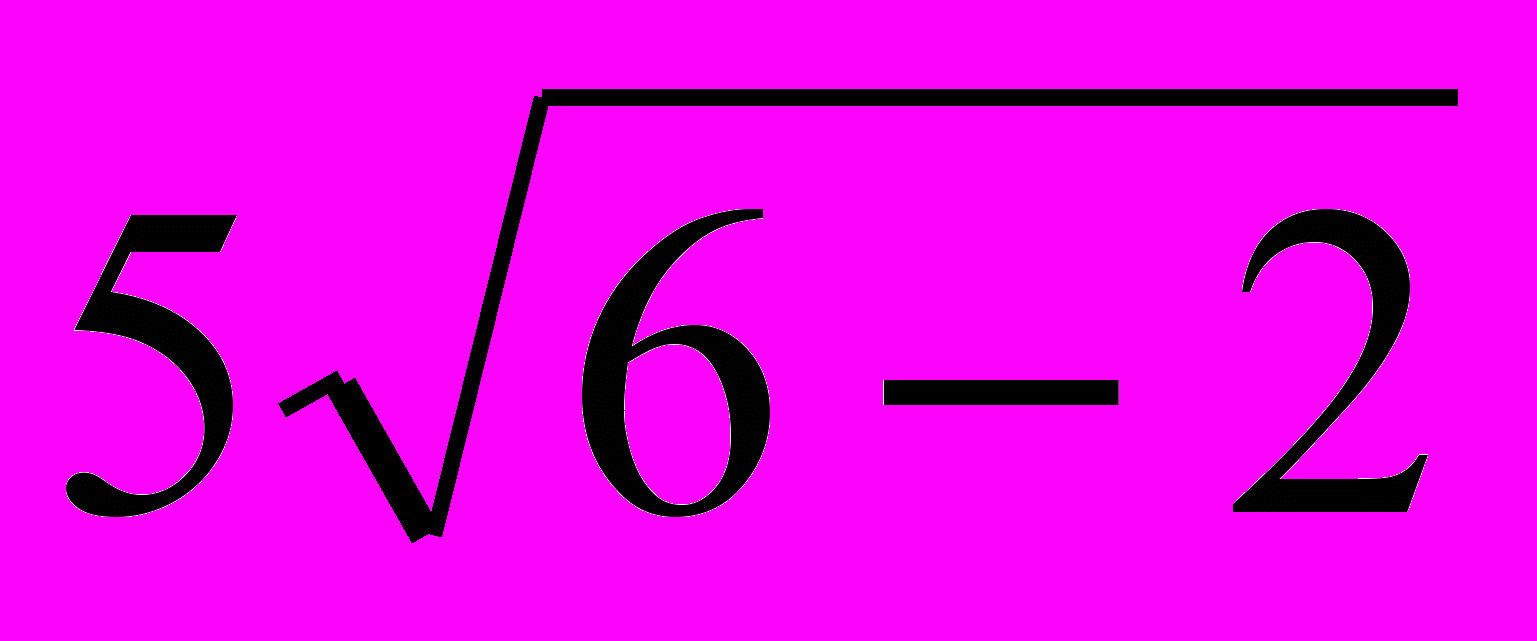+ 4 = 0,

Ответ: 6; 11.

Иррациональные уравнения, которые решаются заменой:

а) Решить уравнение

Решение.

Пусть

= t, тогда

, где t > 0

t –

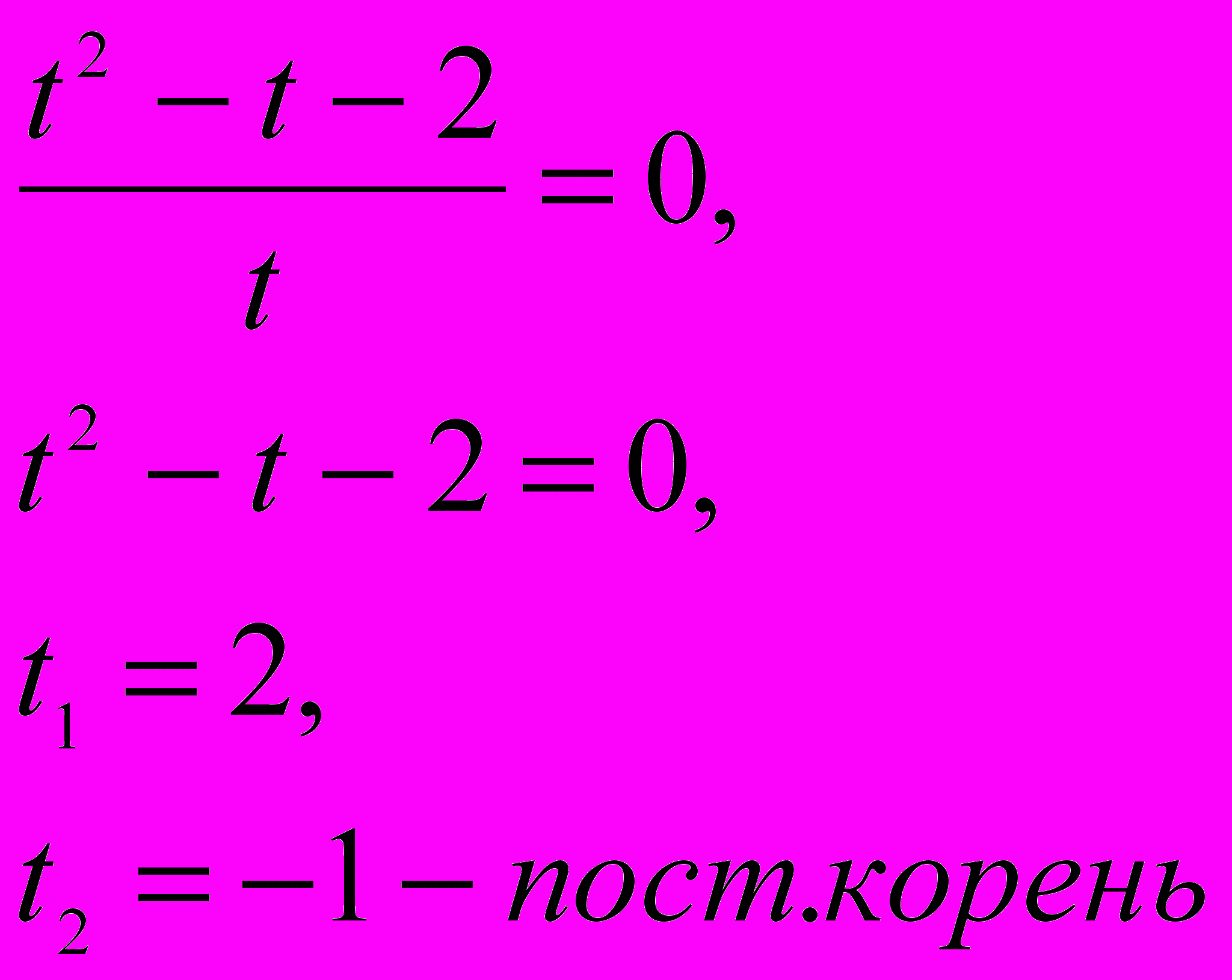
Сделаем обратную замену:

= 2, возведем обе части в квадрат

Проверка: x = 2,5

Ответ: 2,5.

б) Решить уравнение

Решение.

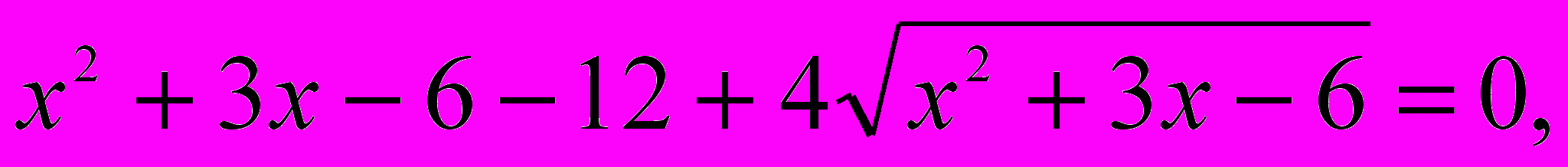
Пусть

= t, где t > 0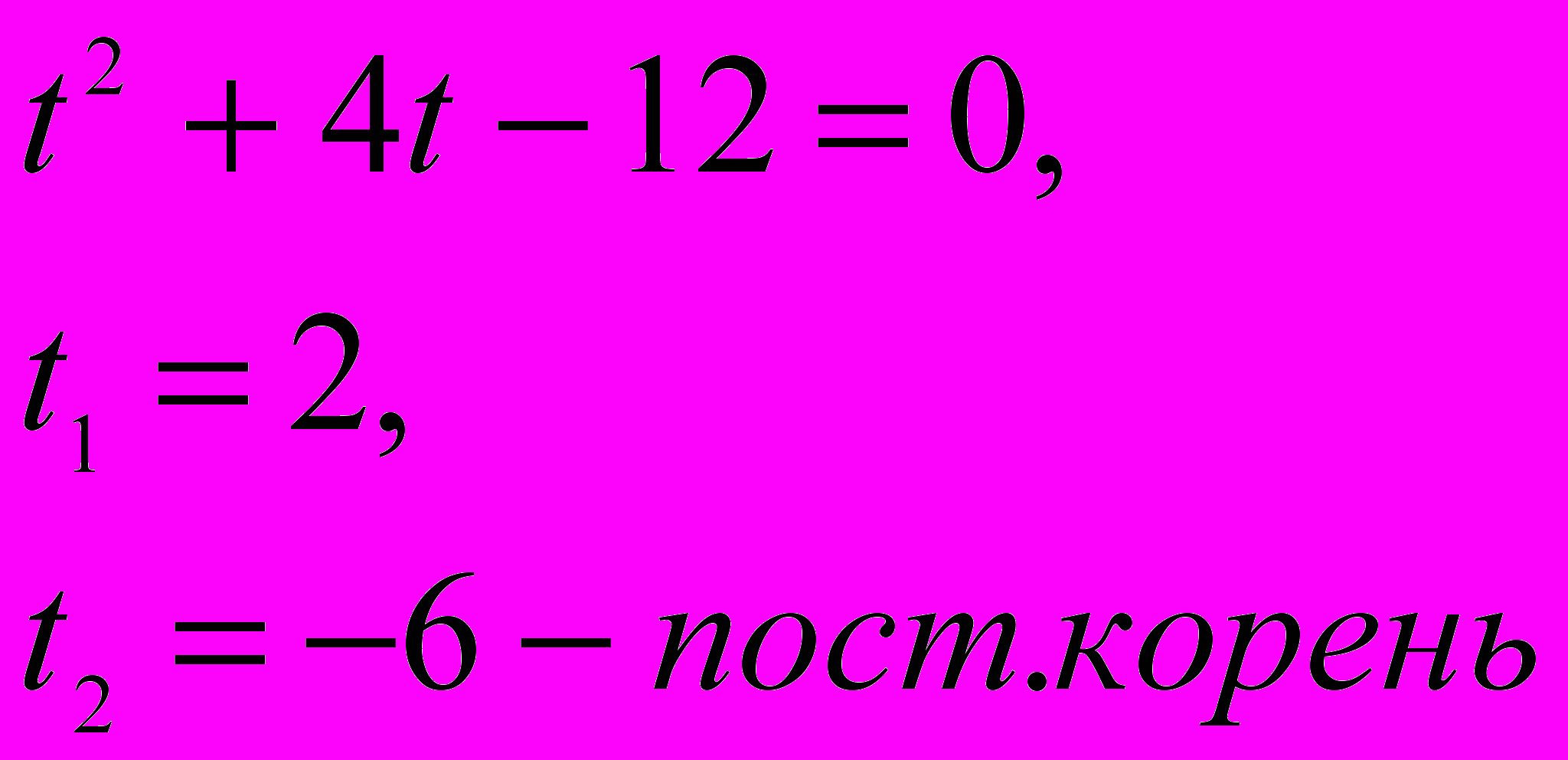

Сделаем обратную замену:

= 2, возведем обе части уравнения в квадрат

Проверка: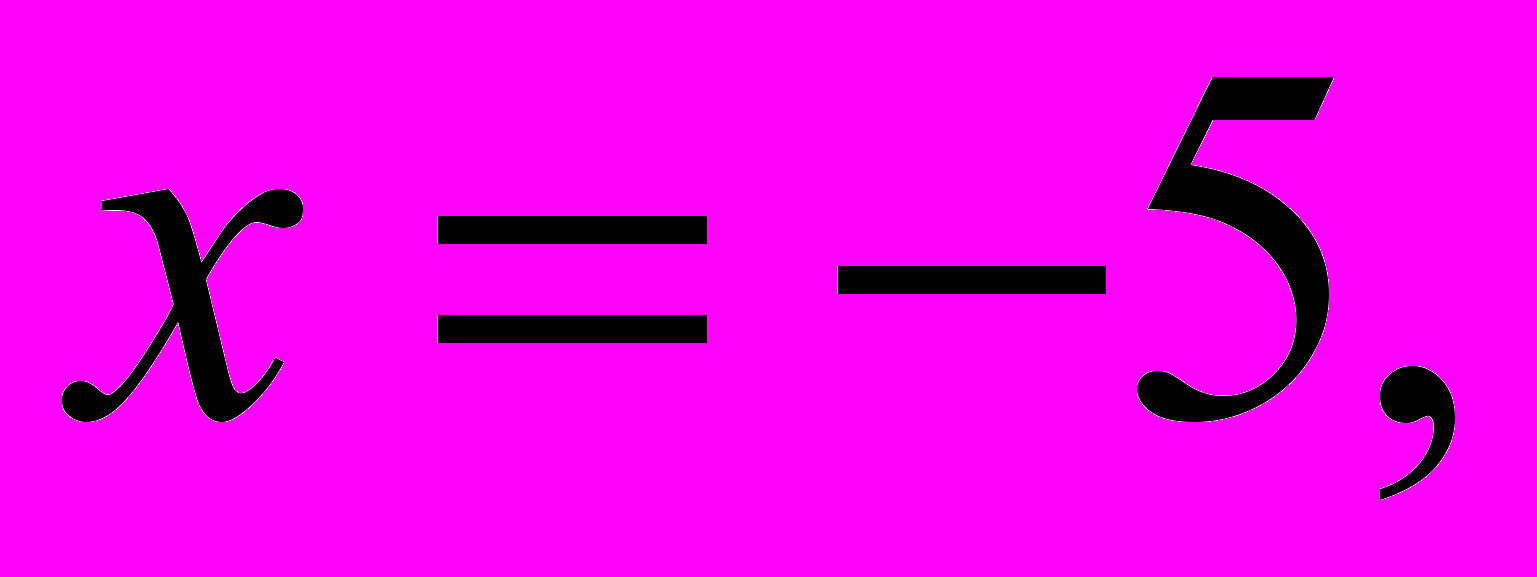

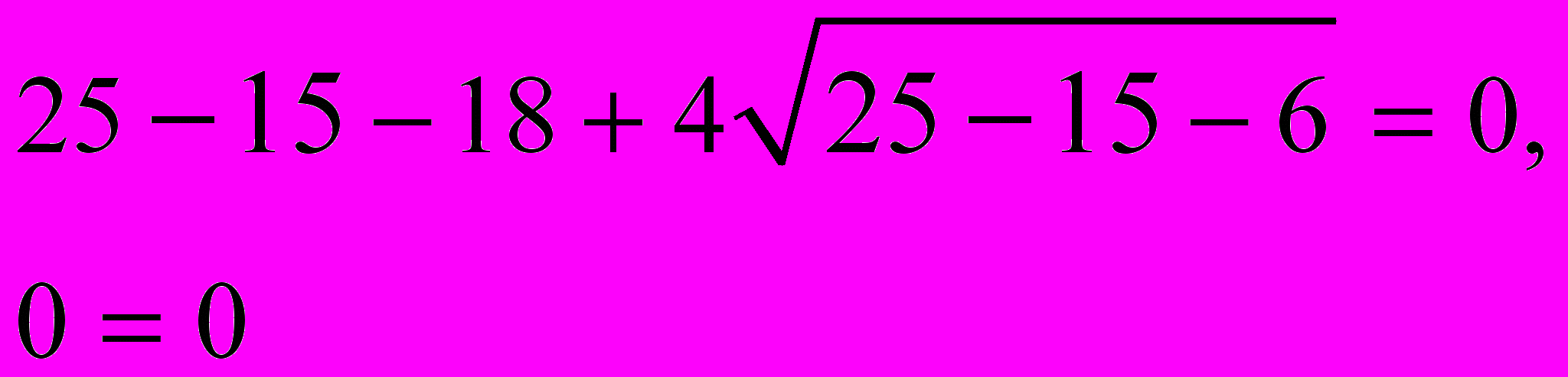
Ответ: –5; 2.

5. Иррациональные неравенства

Неравенства называются иррациональными, если его неизвестное входит под знак корня (радикала).

Иррациональное неравенство вида

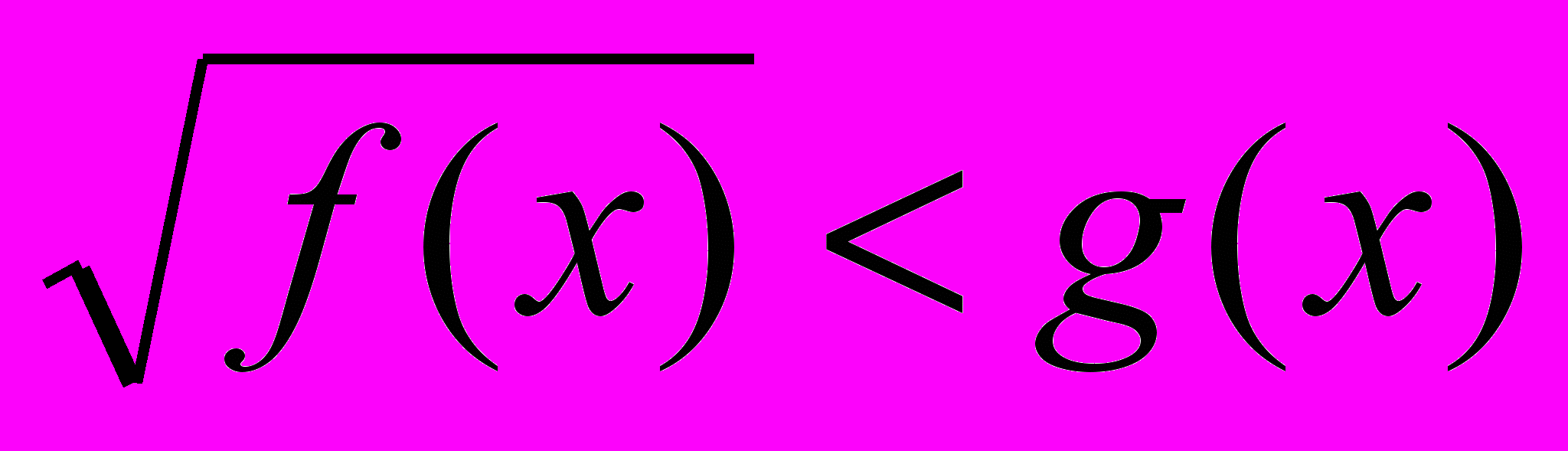равносильно системе неравенств:

Иррациональное неравенство вида

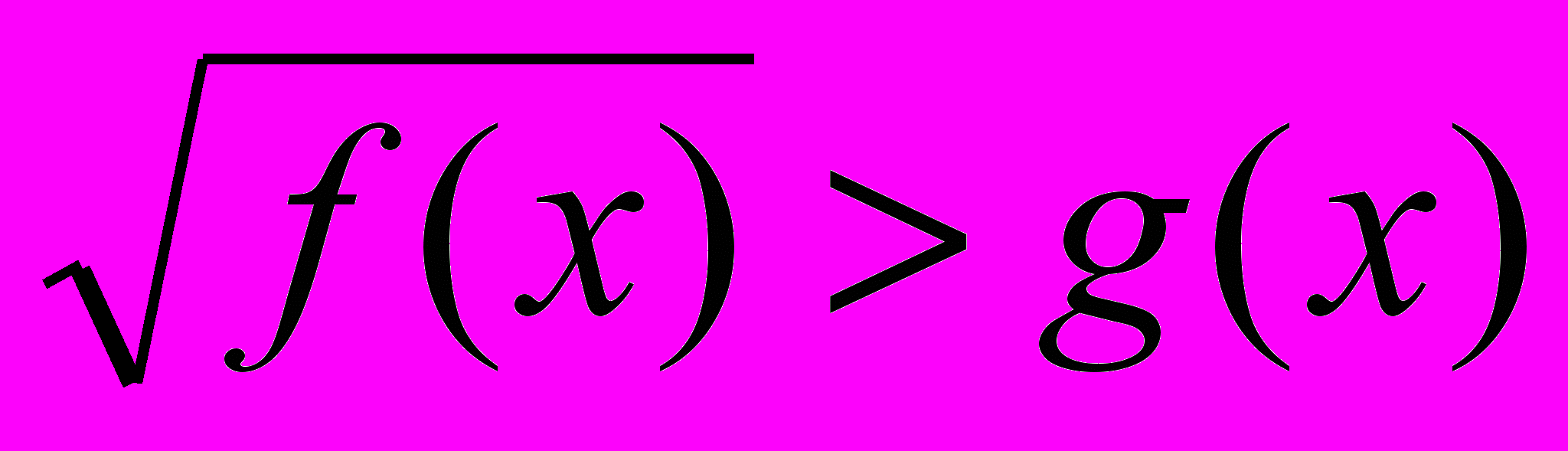равносильно совокупности двух систем неравенств:

5.1 Решение иррациональных неравенств стандартного вида:

а) Решить неравенство

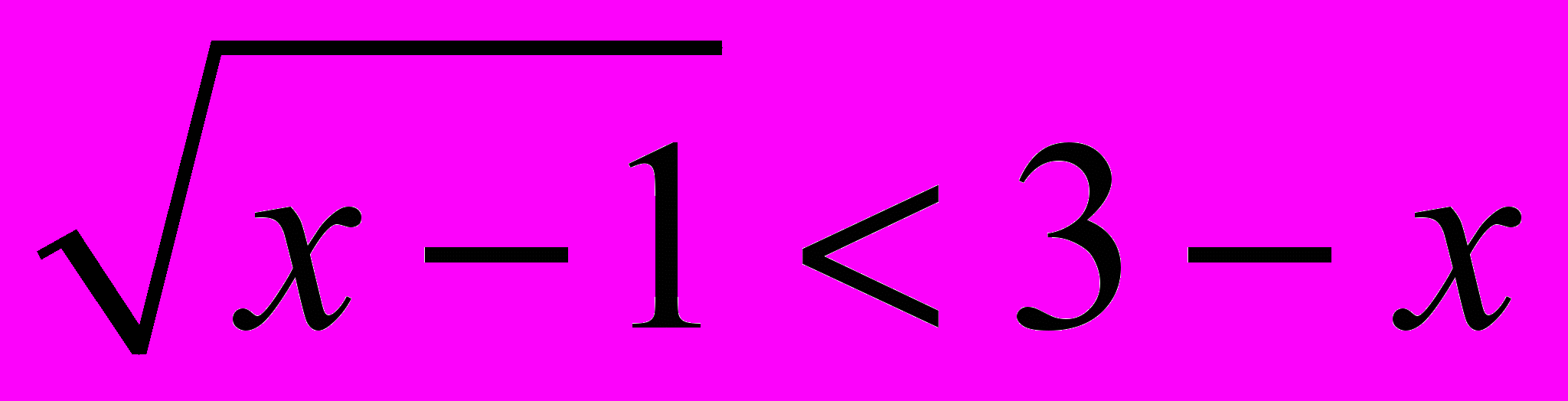
Решение.

Данное неравенство равносильно системе неравенств:

_{+ – +}

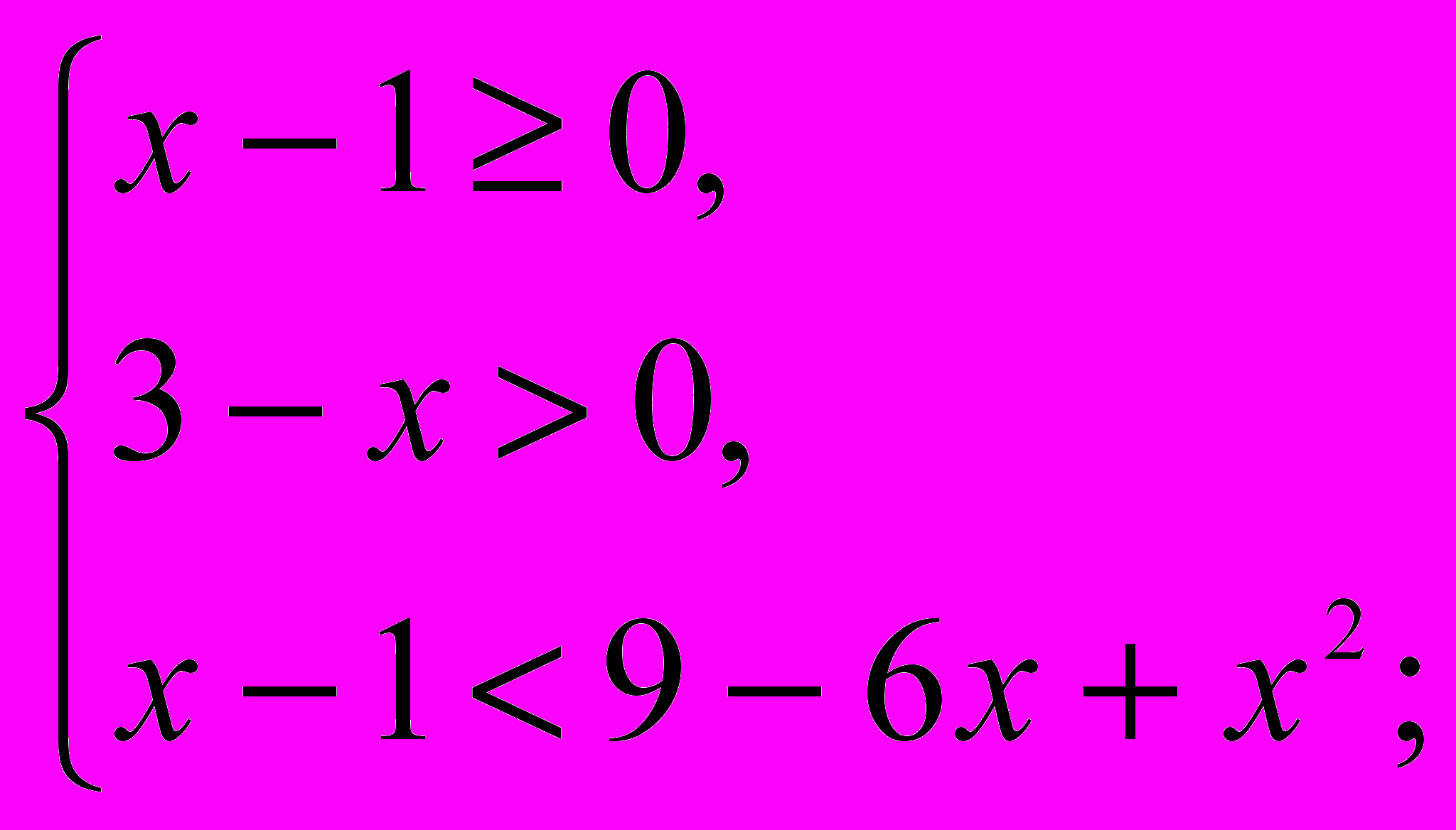
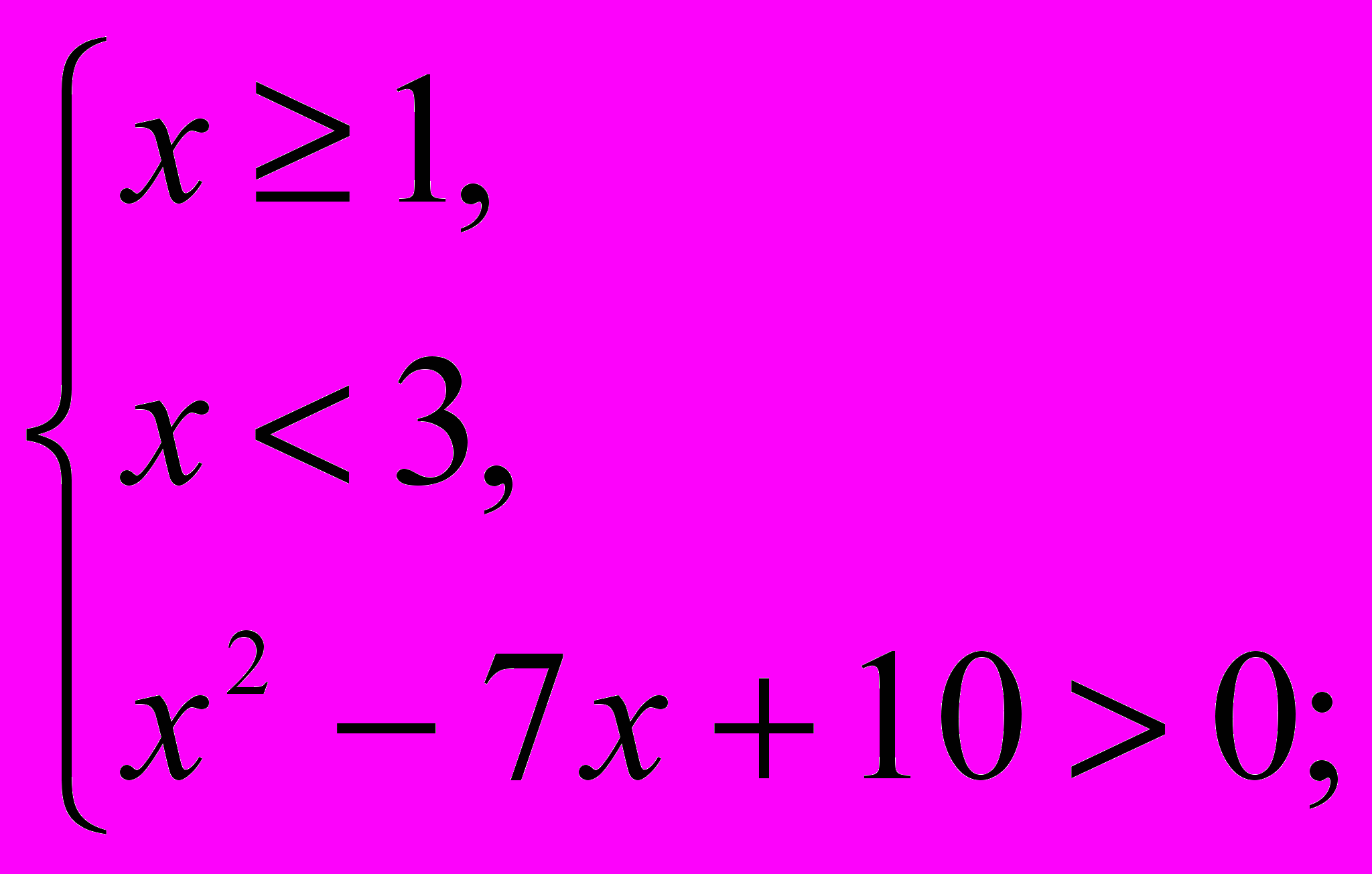
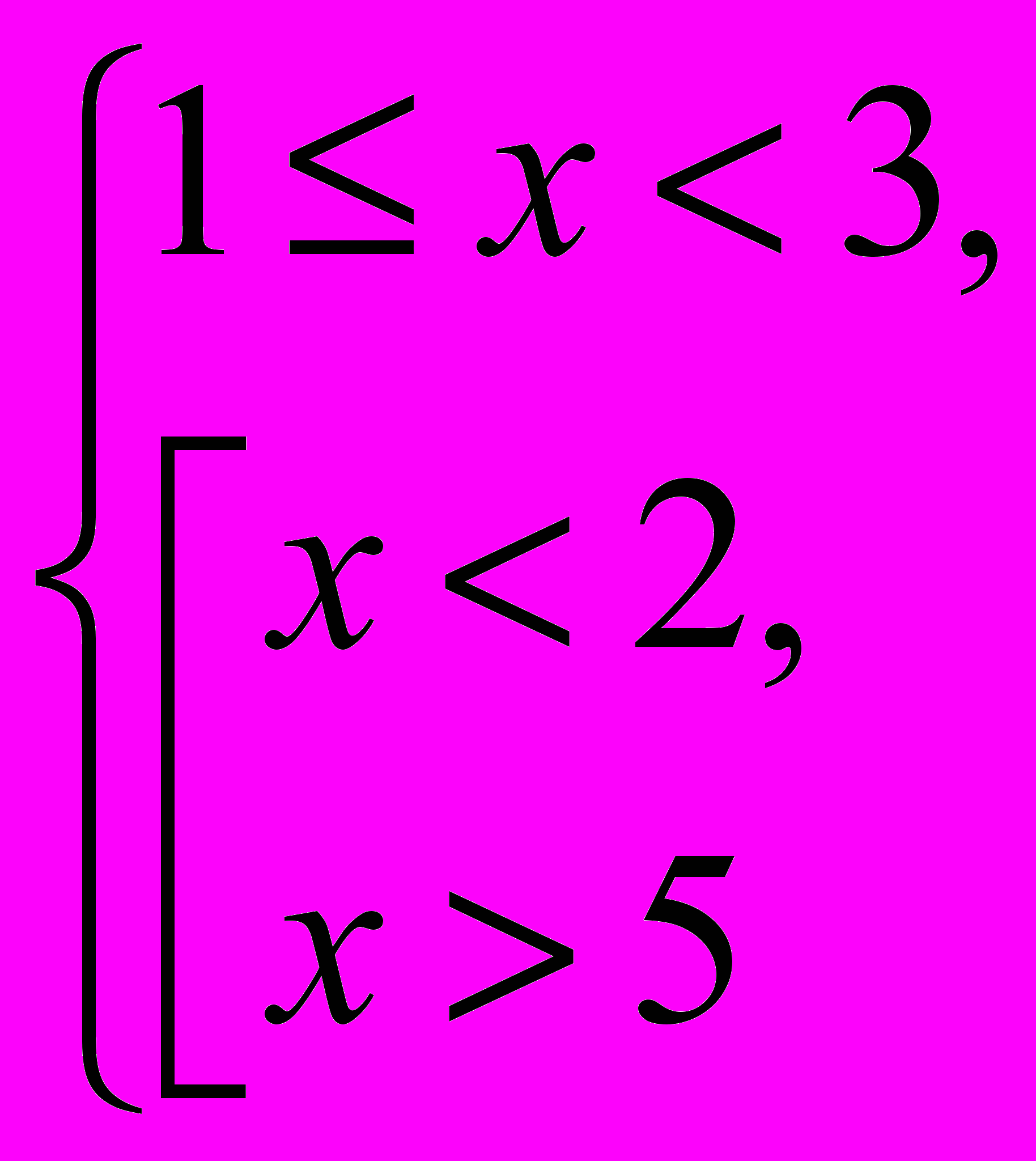
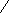
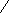
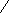
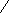
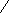
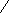
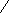
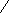
Ответ: [1; 2).1 3 x

б) Решить неравенство

Решение.

Данное неравенство равносильно двум системам неравенств:

Ответ:

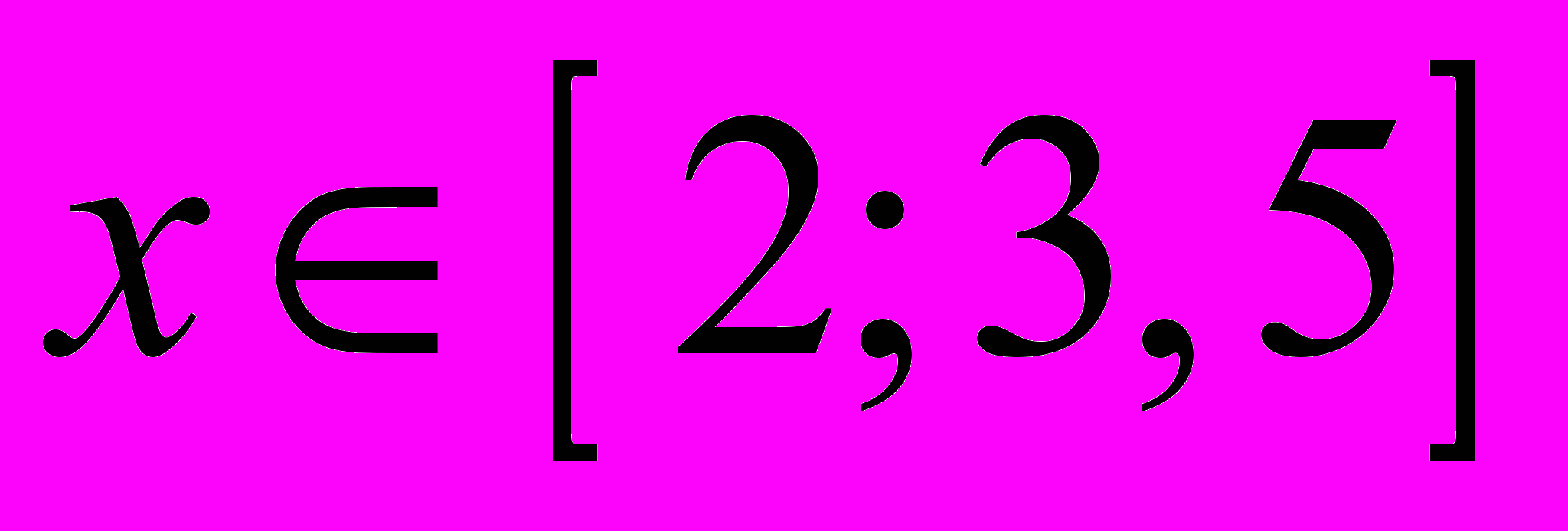
6. Квадратные уравнения и уравнения, сводящиеся к ним

Уравнение вида ax²+bx+c=0,где a,b и c-некоторые числа (а≠0),где x-переменная, называется квадратным уравнением.

Формула решения квадратного уравнения.

Сначала разделим, обе части уравнения ax²+bx+c=0 на a-от этого его корни не изменятся. Для решения получившегося уравнения

x² = (b / a) x + (c / a) = 0

выделим в левой части полный квадрат

x ²+ ( b / a ) = ( c / a ) = ( x² + 2 ( b / 2a ) x+ ( b / 2a )²) + ( c / a ) =

= ( x + ( b / 2a ) )² - ( b² ) / ( 4a² ) = ( c / a ) = ( x + ( b / 2a ))² - ( ( b² - 4ac ) / 4a² ) ).

Для квадратности обозначим выражение (b² - 4ac) через D. Тогда полученное тождество примет вид

x² + ( b / a ) x + ( c / a ) = ( x + ( b / 2a ) )² - ( D / ( 4a² ) ).

Возможны три случая:

если число D положительно (D > 0), то в этом случае можно извлечь из D квадратный корень и записать D в виде D=(√D). Тогда D / (4a²) = (√D)² / (2a)² = (√D / 2a)², поэтому тождество принимает вид

x² + ( b / a ) x + ( c / a ) = ( x + ( b / 2a ))²- ( √D / 2a )².

По формуле разности квадратов выводим отсюда:

x² + ( b / a ) x + ( c / a ) = ( x + ( b / 2a ) – ( √D / 2a )) (x + ( b / 2a )) = ( x – ((- b + √D ) / 2a )) ( x – (( - b - √D ) / 2a )).

Теорема: Если выполняется тождество

ax² + bx + c = a (x – x) (x – x2),

то квадратное уравнение ax² + bx + c = 0 при X ≠ X2 имеет два корня X и

X2 , а при X + X2 - лишь один корень X. В силу этой теоремы из, выведенного выше, тождество следует, что уравнение x² + (b / a) x + (c / a)=0, а тем самым и уравнение ax² + bx + c = 0, имеет два корня:

X = (- b + √D) / 2a; X2 = (- b - √D) / 2a.

Таким образом, x² + (b / a) x + (c / a) = (x - x) (x - x2).

Обычно эти корни записывают одной формулой:

X, 2 = -b ±√b² - 4ac / 2a где b² - 4ac = D.

2) если число D равно нулю (D = 0), то тождество

x² + ( b / a ) x + ( c / a ) = ( x + ( b / 2a ) )² - ( D / ( 4a² ) ).

принимает вид

x² + ( b / a ) x + ( c / a ) = ( x + ( b / 2a ) )².

Отсюда следует, что при D = 0 уравнение ax² + bx + c = 0 имеет один корень кратности 2: X = - b / 2a;

3) если число D отрицательно (D < 0),то и поэтому выражение

x² + ( b / a ) x + ( c / a ) = ( x + ( b / 2a ) )² - ( D / ( 4a² ) ).

является суммой двух слагаемых, одно из которых неотрицательно, а другое положительно. Такая сумма не может равняться нулю, поэтому уравнение

x² + (b / a) x + (c / a) = 0

не имеет действительных корней. Не имеет их и уравнение

ax² + bx + с = 0. Таким образом, для решения квадратного уравнения следует вычислить дискриминант D = b² - 4ac.

Если D = 0, то квадратное уравнение имеет единственное решение:

X = - b / (2a).

Если D > 0, то квадратное уравнение имеет два корня:

X = (- b + √D) / 2a; X2 = (- b - √D) / 2a.

Если D < 0, то квадратное уравнение не имеет корней.

Если один из коэффициентов b или c равен пулю, то квадратное уравнение можно решать, не вычисляя дискриминанта:

b = 0; c ≠ 0: c / a < 0: X,2 = ± /√(-c / a )
b ≠ 0; c = 0: X = 0, X2 = - b / a

Квадратное уравнение, в котором коэффициент при x² равен 1, называются приведенным. Обычно приведенное квадратное уравнение обозначают так:

x² + px +q =0.

Корни приведенного квадратного уравнения обычно находятся по формуле

X, 2 = -p/2 ± √ (p / 2)²- q

6.1 Теорема Виета

Мы вывели тождество

x² + (b / a) x + (c / a) = (x - x) (x - x2),

где – корни квадратного уравнения ax² + bx + c = 0. раскроем скобки в первой части этого тождества.

x² + (b / a) x + (c / a) = x² - xx – x2x + xx2 = x² - (x + x) x + x x2.

отсюда следует, что Мы доказали следующую теорему, впервые установленную французским математиком Ф. Виетом (1540 – 2603):

Теорема 1 (Виета). Сумма корней квадратного уравнения равна коэффициенту при X, взятому с противоположным знаком и деленному на коэффициент при X²; произведение корней этого уравнения равно свободному члену, деленному на коэффициент при X².

Теорема 2 (обратная). Если выполняется равенства

X + X2 = -b / a и XX2 = c / a,

то числа X и X2 являются корнями квадратного уравнения ax² + bx + с = 0.

Замечание. Формулы X + X2 = -b / a и XX2 = c / a остаются верными и в случае, когда уравнение ax² + bx + с = 0 имеет один корень X кратности 2, если положить в указанных формулах X2 = X. Поэтому принято считать, что при D = 0 уравнение ax² + bx + с = 0 имеет совпадающих друг с другом корня.

При решении задач, связанных с теоремой Виета, полезно использовать соотношения

(1 / X) + (1 / X2) = (X + X2) / XX2;

X² + X2² = (X + X2) – 2XX2;

X / X2 + X / X2 = (X² + X2²) / XX2 = ((X + X2)² - 2XX2 / XX2;

X³ + X2³ = (X + X2) (X² – XX2 + X2²) = (X +X2) ((X + X2)² - 3XX2).

Пример 1. Решить уравнение 2x² + 5x – 1 = 0

Решение.D = 25 – 42(-1) = 33 > 0; X = (-5 + √33) / 4; X2 = (-5 - √33) / 4.

Пример 2. решить уравнение x³ -5x² + 6x = 0

Решение. Разложим левую часть уравнения на множители x (x² – 5x +6) = 0,отсюда x = 0 или x² – 5x + 6 = 0.

Решая квадратное уравнение, получаем X = 2, X2 = 3.

Ответ: 0; 2; 3

Заключение

Выделенным областям возникновения и функционирования понятия
уравнения в алгебре соответствуют три основных направления развертывания линии уравнений и неравенств в школьном курсе математики.
а) Прикладная направленность линии уравнений раскрывается главным образом при изучении алгебраического метода решения текстовых задач.

Этот метод широко применяется в школьной математике, поскольку он связан с обучением приемам, используемым в приложениях математики.
В настоящее время, ведущее положение в приложениях математики занимает математическое моделирование. Используя это понятие, можно сказать, что прикладное значение уравнений, их систем определяется тем, что они являются основной частью математических средств, используемых в математическом моделировании.

б) Теоретико-математическая направленность линии уравнений
раскрывается в двух аспектах: во-первых, в изучении наиболее важных классов уравнений, и их систем и, во-вторых, в изучении обобщенных понятий и методов, относящихся к линии в целом. Оба эти аспекта необходимы в курсе школьной математики. Основные классы уравнений связаны с простейшими и одновременно наиболее важными математическими моделями. Использование обобщенных понятий и методов позволяет логически упорядочить изучение
линии в целом, поскольку они описывают то общее, что имеется процедурах и приемах решения, относящихся к отдельным классам уравнений, неравенств, систем. В свою очередь, эти общие понятия и методы опираются на основные логические понятия: неизвестное, равенство, равносильность, логическое следование, которые также должны быть раскрыты в линии уравнений.

Список используемой литературы

В.А. Любецкий Основные понятия школьной математики, изд. «Просвещение» 1987г.
В.С Крамор Повторяем и систематизируем школьный курс алгебры и начал анализа, изд. «Просвещение» 1990г.
Г.И. Глейзер «История математики в школе 7-8 классов» 1982г.
Задачи по математике. Уравнения и неравенства. ВавиловК. И. Мельников И.И. изд. «Наука» 1987г.
Алгебра и математический анализ. 10 класс. Н. Я. Виленкин. Москва, изд. «Просвещение».

Перейти к оглавлению

Blog

Владимирова Наталья Анатольевна Студентка 23 группы уравнения и неравенства в школьном курсе математики реферат

Содержание