Поповская Анна Владимировна Студент 23 группы Методика обучения учащихся векторному методу в школьном курсе геометрии реферат
| Вид материала | Реферат |
- Методика обучения решению прикладных задач в школьном курсе математики примерное содержание, 14.61kb.
- Владимирова Наталья Анатольевна Студентка 23 группы уравнения и неравенства в школьном, 176.4kb.
- Методика изучения электродинамики в школьном курсе физики раздел «электродинамика», 808.93kb.
- Темы контрольных работ по дисциплине «Теория и методика обучения географии» а для студентов, 23.25kb.
- Тема 12. Методика изучения темы, 252.36kb.
- Система знаний о микроорганизмах в школьном курсе биологии как основа формирования, 325.99kb.
- Тольяттинский Государственный Университет Кафедра методики преподавания физики и физической, 381.94kb.
- Методика изучения темы: «Элементы статистики, комбинаторики и теории вероятностей, 1031.61kb.
- Методика математики 5-6 классов и алгебры 7-9 классов (34ч) Занятие Изучение натуральных, 180.88kb.
- Дидактическое пособие для учащихся по изучению цитологии в школьном курсе биологии, 260.51kb.
управление образования и науки белгородской области
Валуйский педагогический колледж
Школьное отделение

Предметно-цикловая комиссия физико-математических дисциплин
Поповская Анна Владимировна
Студент 23 группы
Методика обучения учащихся векторному методу в школьном курсе геометрии
РЕФЕРАТ
По специальности 05020152 – преподавание математики в основной школе
Квалификация – учитель математики основной школы
Научный руководитель:
Преподаватель Соколова С. В.
Валуйки, 2007
План:
Введение
I 1.1 История векторного исчисления.
1.2.Понятие вектора. Цели изучения векторного метода в средней школе.
1.3.Основные компоненты векторного метода решения задач.
1.4.Понятийный аппарат.
1.5.Основные этапы формирования векторного метода у учащихся.
1.6.Методика формирования векторного метода решения задач.
II 2.1.Решение задач.
Заключение
Список литературы
Введение
В настоящее время в разных странах существует более или менее единое мнение по следующим двум вопросам:
- Преподавание геометрии не может основываться на дедукции. Оно должно быть основано на наблюдении; его целью является выработка фундаментальных понятий, базирующихся на опыте.
- Самый элегантный, глубокий и быстрый способ определения плоскости (или пространства) для математика – это определение её как двумерного (трёхмерного) векторного пространства над R, снабженного скалярным произведением. Кроме того, именно это определение наилучшим образом подготовлено для плодотворных обобщений.
Мы должны отдать предпочтение методам, основанными на фундаментальных понятиях, выкристаллизовавших за двадцать веков развития математики: понятиях множества, отношений эквивалентности и порядка, алгебраических законах, векторном пространстве, симметрии и геометрических преобразований.
Как построить схему, удовлетворяющую нашим требованиям? Хотелось бы, чтобы в этой системе было удобно выявить векторную структуру пространства, равно как и существование и свойства скалярного произведения. Следовательно, ситуацию можно резюмировать следующим образом: сегодня мы владеем простым «царским путем» в геометрию, ведущим через понятия «векторного пространства» и «скалярного произведения»; однако этими понятиями нельзя «овладеть штурмом», без всякой подготовки. Тем не менее, эти понятия будут служить нам путеводной звездой.
Основные цели данного метода:
- рассмотреть цели изучения векторного метода в школе;
- выделить основные компоненты решения задач этим методом;
- рассмотреть понятийный аппарат векторного метода решения задач.
1.1.История векторного исчисления
Многие историки считают «родителями векторного пространства» ирландского учёного XIX в. У. Гамильтона, а также его немецких коллег и современников Г. Грассмана. Даже сам термин «вектор» ввел также Гамильтон около 1845 г.
Между тем историю векторного исчисления, как историю и корни всякой крупной математической теории, можно проследить задолго до его выделения в самостоятельный раздел математики. Так еще Архимед в его всем известном законе присутствует величина, характеризующаяся не только численным значением, но и направлением. Более того: векторный характер сил, скоростей и перемещений в пространстве был знаком многим ученым Античного времени, а «правило параллелограмма» сложения векторов было известно еще в IV в. Р. Х. математикам школы Аристотеля. Вектор обычно изображался отрезком с указанным на нем направлением, т.е. направленным отрезком.
Параллельно с исследованиями комплексных чисел в работах многих математиков XVII-XVIII в. в., занимавшихся геометрическими проблемами, можно увидеть нарастание потребности в неком геометрическом исчислении, подобном численному (исчислению действительных чисел), но связанному с пространственной системой координат. Его в какой-то мере пытался создать еще Лейбниц, продумывая свою «универсальную арифметику», но, несмотря на гениальность и необычайную широту интересов, сделать это ему не удалось. Однако уже к концу XVIII в. отдельные идеи векторного исчисления, которое и стало тем исчислением, что искали геометры, смог сформулировать французский ученый Л. Карно. А в 30-х годах XIX в. у Гамильтона и Грассмана в работах по теории комплексных чисел и кватернионов эти идеи были сформулированы уже совершенно прозрачно, хотя, по существу, что удивительно, они имели дело только с некоторыми примерами тех конечномерных векторных пространств, которые теперь бы мы назвали – координатными.
Так называемые функциональные векторные пространства привлекли внимание математиков уже в начале нашего века рослее инновационных результатов в этой области итальянца С. Пинкерля и немецкого математика О. Теплица, который известен своими работами по теории матриц, и, в частности, тем, что придумал удачную общую модель векторного пространства – координатное векторное пространство. Именно Хевисайд ввел в 1891 г. Одно из закрепившихся в научной литературе обозначающий вектора: а, автором двух других общепринятых ныне обозначений векторов: ā был Ж. Арган, а для обозначения свободного вектора предложил А. Мебиус. Термин «скалярный» в современном смысле впервые употребил У. Гамильтон в 1843 г.
Таким образом, векторное исчисление – это раздел математики, в котором изучаются свойства операций над векторами. Векторное исчисление подразделяют на векторную алгебру и векторный анализ. Возникновение векторного исчисления тесно связано с потребностями механики и физики.
2.2 Понятие вектор. Цели изучения векторного метода в средней школе
Вектор – одно из фундаментальных понятий современной математики и широко используется в различных её областях. В работах Г. Бесселя, Ж. Аргана и К. Гаусса по теории комплексных чисел установлена связь между арифметическими операциями над векторами в двумерном пространстве. В работах В. Гамильтона, Г. Грассмана, Ф. Мёбиуса понятие вектора нашло широкое применение при изучении свойств трёхмерного пространства. В настоящее время на векторной основе излагаются линейная алгебра, аналитическая и дифференциональная геометрия, функциональный анализ.
К понятию вектора как направленного отрезка приводят многие задачи механики и других областей физики: теории упругости, теории электромагнитных полей.
В методике преподавания математики вектор выступает как связывающее звено между метрикой и направлением.
Цели изучения векторного метода в средней школе:
- дать эффективный метод решения различных геометрических задач (как аффинных, так и метрических) и доказательства теорем;
- показать широкое применение векторного аппарата в других областях знаний: технике, физике, химии, лингвистике – и на базе этого форматировать у учащихся диалектико-материалистическое мировоззрение;
- использовать векторный метод при решении задач с целью форматирования у учащихся выполнять обобщение и конкретизацию;
- формировать у учащихся такие качества мышления, как гибкость (нешаблонность), целенаправленность, рациональность, критичность и др.
2.3.Основные компоненты векторного метода решения задач
Основными компонентами векторного решения метода решения задач являются:
- перевод условия задачи на язык векторов, в том числе:
- введение в рассмотрение векторов;
- выбор системы координат (если это необходимо);
- выбор базисных векторов;
- разложение всех введенных векторов
- введение в рассмотрение векторов;
- составление системы векторных равенств (или одного равенства). Заметим, что в школе чаще используются векторные тождества и их преобразования, реже – векторные уравнения. Поэтому используется термин «равенство».
- упрощение векторных равенств
- замена векторных равенств алгебраическими уравнениями и их решения
- объяснение геометрического смысла полученного решения этой системы (или одного уравнения).
2.4.Понятийный аппарат
Понятийный аппарат и умения, которыми должен овладать ученик, чтобы научиться решать задачи векторным методом:
- основные понятия: вектор, начало вектора, конец вектора, одинаково направленные векторы, противоположно направленные векторы, абсолютная величина вектора (модуль вектора), равные векторы, нулевой вектор, неколлинеарные векторы, единичный вектор, координатные векторы (орты), скалярное произведение векторов, угол между ненулевыми векторами;
- основные действия, умение выполнять которые должно быть сформулировано у учащихся: сложение векторов (пользуясь «правилом треугольника», «правилом параллелограмма» и «правилом параллепипеда»); вычитание векторов; умножение векторов на число; представление вектора в виде суммы, разности двух векторов, в виде произведения вектора на число; замена вектора ему равным при помощи параллельного переноса; представление вектора в виде его разложения по двум неколлинеарным векторам; переход от соотношения между векторами к соотношению между их длинами и выполнение обратного действия; выражение величины угла между векторами через скалярное произведение векторов и длины этих векторов;
- действия для овладения компонентами метода: перевод геометрических терминов на язык векторов и решение обратной задачи; перевод условия задачи на язык векторов, т.е. составление системы векторных равенств по условию задачи; выбор базисных векторов, разложение всех введенных в рассмотрение векторов по базисным векторам; упрощение системы векторных равенств; замена векторных равенств алгебраическими.
2.5.Основные этапы формирования векторного метода у учащихся
Подготовительный этап. Его цель – овладение перечисленными основными понятиями и основными действиями.
Мотивационный этап. Его задача – показать необходимость овладения этим методом и добиться осознания того факта, что на следующих этапах целью деятельности учащихся будет именно усвоение этого метода решения задач. Приём, используемый при этом, - решение таких задач, которые векторным методом решаются проще, чем любым другим, или другим вообще решить невозможно.
Ориентировочный этап. Его цель – разъяснить суть метода и выделить его основные компоненты на примере анализа решенной этим методом задачи.
Этап овладения компонентами метода. Цель – используя специально подобранные задачи, формировать отдельные компоненты метода (сначала задачи на формирование одного компонента, потом двух, трёх и т.д.).
Этап формирования метода «в целом». Цель – решение задач, в которых работают все или большинство компонентов метода (в том числе и на материале физики, химии и др. предметов).
Деление форматирования метода на этапы здесь условно, т.к. они тесно взаимосвязаны. Очевидно, не стоит разделять ученикам четко задачи на формирование компонентов, но сам учитель должен четко знать, какой компонент с помощью какой из задач он будет формировать у учащихся. Однако цель каждого этапа должна быть ясна и учителю, и учащимся.
2.6.Методика формирования векторного метода решения задач
- Подготовительный этап формирования метода (понятийный аппарат, основные понятия и основные действия) имеется в каждом из рассматриваемых учебных пособий, хотя он и не сосредоточен на каком-либо коротком промежутке времени.
- На мотивационном этапе можно рассмотреть с учащимися решение следующей задачи:
Задача: В трапеции ABCD углы A и B равны по 900, а стороны AB=2, BC=1, AD=4. окажите, что диагонали этой трапеции взаимно перпендикулярны.
Задача решается несколькими способами и показывается, что векторный метод задачи более прост.
- На примере решения задачи проведите ориентировочный этап, т.е. разъясните суть метода и покажите его основные компоненты:
- Выясняется, что нужно доказать на геометрическом языке.
- Что для этого достаточно доказать на векторном языке?
- Какую операцию осуществил
- Что для этого достаточно доказать на векторном языке?
- Есть ли в условии задачи векторы AC и BD?
- Выясняется, что нужно доказать на геометрическом языке.
- Каким образом можно получить векторы AC и BD?
- Записывается скалярное произведение векторов.
- Выполняется преобразования и получается, что AC*BD= 0.
- Переводится векторное равенство на геометрический язык.
Показывается, какому необходимо научить учащихся, - это перевод геометрических соотношений на векторный язык. Для формирования умения выполнять это действие целесообразно с учащимися решать задачи типа:
- Точка А принадлежит отрезку ВС. Запишите это соотношение в векторной форме. (ВА=α*ВС, 0< α<1)
- Запишите в векторной форме условие перпендикулярности прямых АВ и РК (АВ*РК=0)
Решение этих и других подобных задач желательно оформить в виде таблицы в кабинете и первое время ею пользоваться при решении задач векторным способом.
Учащимся показывается наиболее целесообразный выбор системы координат и выбор базисных векторов.
Это действие формируется у учащихся с помощью задач:
- Найдите угол между вектором ā (1;-2) и b (-3;1)
- Четыре точки заданы своими координатами: А (3;1), В (1;4), С (1;0), Д (4;5). Определите угол между прямыми АВ и СД.
2.1.Линейные операции над векторами
Линейные операции называются операции сложения и вычитания векторов и умножение вектора на число.
- Сумма векторов
Определение 1.Пусть
 и
и  - два свободных вектора. Возьмём произвольную точку О и построим вектор
- два свободных вектора. Возьмём произвольную точку О и построим вектор 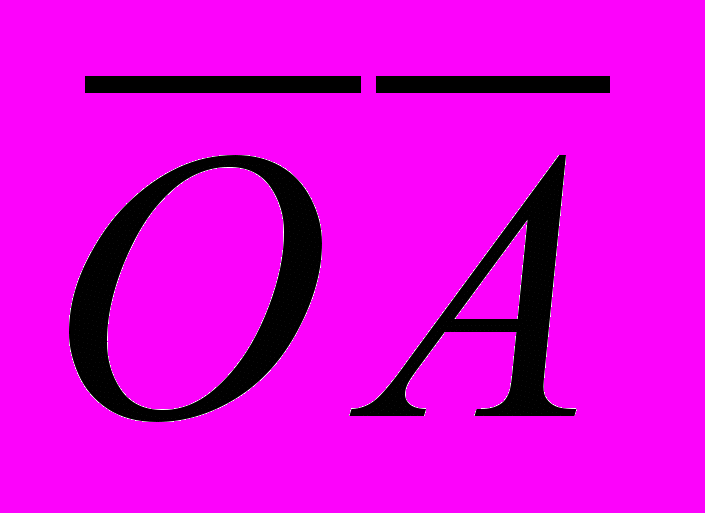 =
= , в затем от точки А отложим вектор
, в затем от точки А отложим вектор 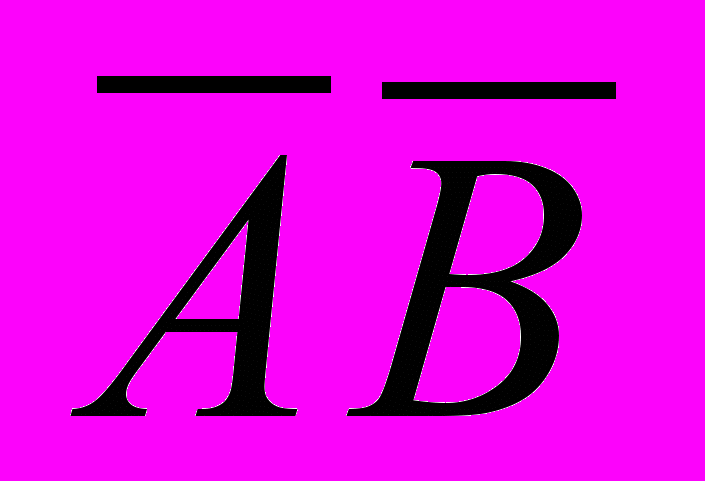 =
= . Вектор
. Вектор 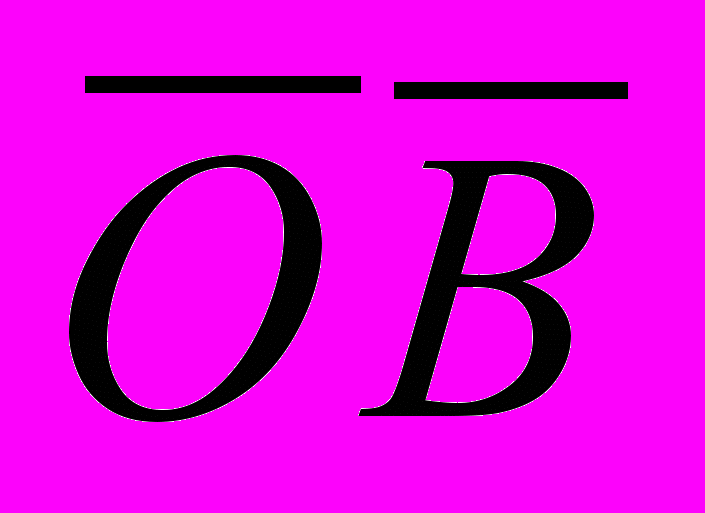 , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается
, соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается  +
+ .
.Это правило построения суммы двух векторов называется «правилом треугольника».
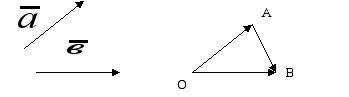
Определение 2.Суммой векторов
 и
и  с координатами а1, а2 и в1, в2 называется вектор с координатами а1+в1, а2+в2, т.е.
с координатами а1, а2 и в1, в2 называется вектор с координатами а1+в1, а2+в2, т.е. (а1; а2)+
(а1; а2)+  (в1; в2) =
(в1; в2) =  (а1+в1; а2+в2).
(а1+в1; а2+в2).Ту же самую сумму векторов можно получить иным способом.
Отложим от точки О вектор
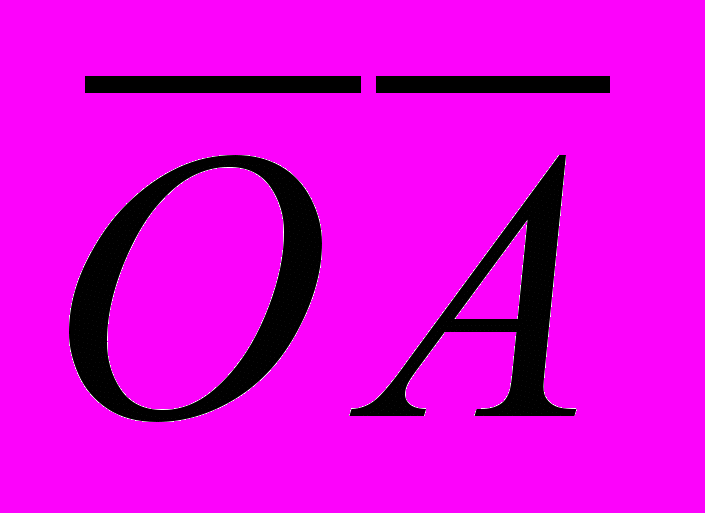 =
= и
и 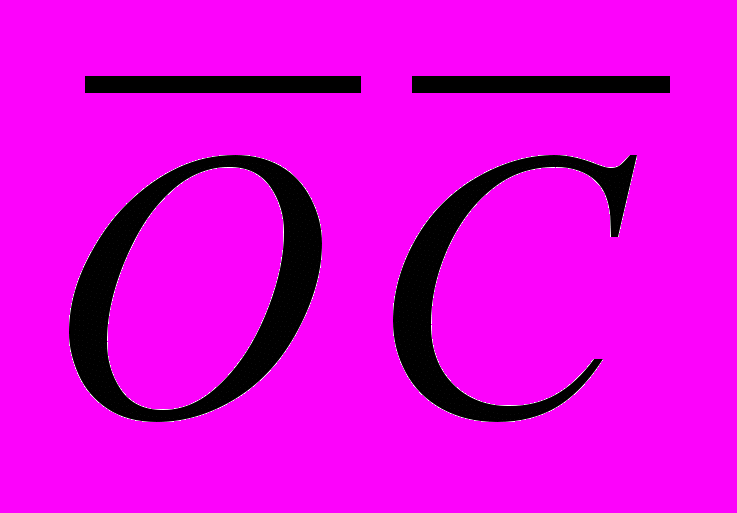 =
= . Построим на этих векторах как на сторонах параллелограмм ОАВС. Вектор
. Построим на этих векторах как на сторонах параллелограмм ОАВС. Вектор 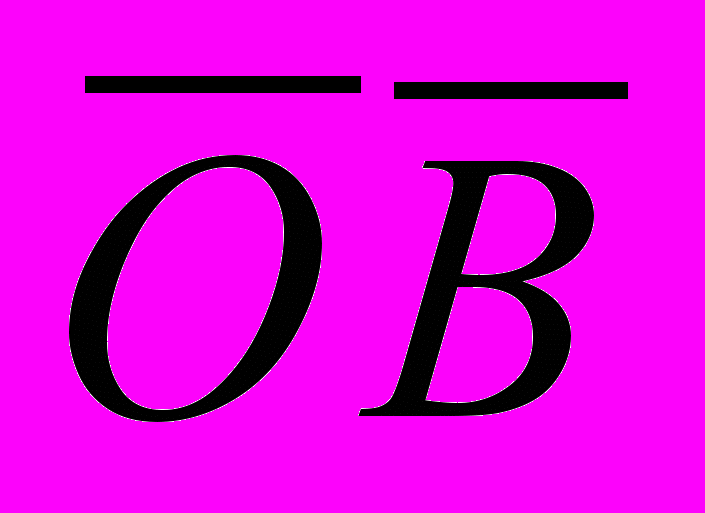 , служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов
, служащий диагональю этого параллелограмма, проведенной из вершины О, является, очевидно, суммой векторов  +
+ . Из рисунка непосредственно следует, что сумма двух векторов обладает переместительным свойством:
. Из рисунка непосредственно следует, что сумма двух векторов обладает переместительным свойством: +
+ =
= +
+
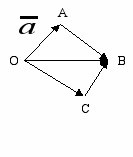
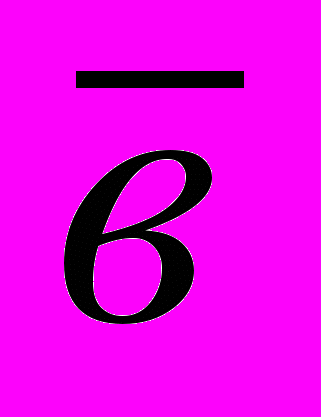
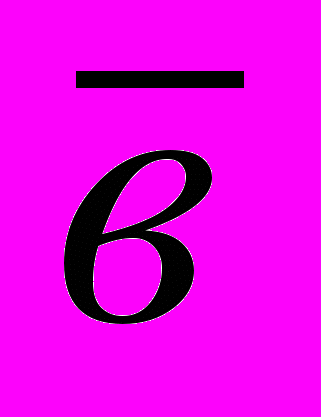

Сумма двух векторов, исходящих из одной точки, выполняется по «правилу параллелограмма».
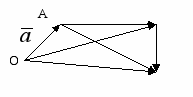
Пусть, например, даны три вектора
 ,
,  и
и  .
.
П
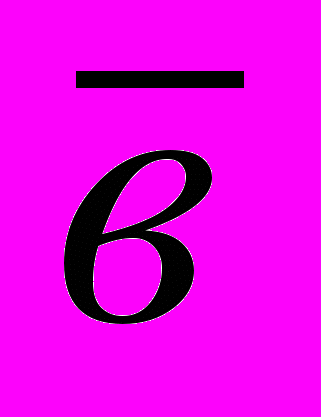
остроим сначала сумму векторов
 +
+ , а затем, прибавив к этой сумме
, а затем, прибавив к этой сумме  , получим вектор (
, получим вектор ( +
+ )+
)+ . На рисунке
. На рисунке 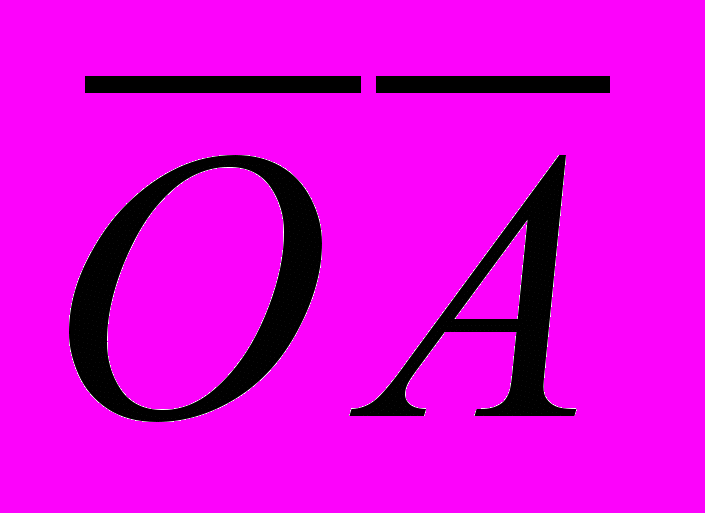 =
= ,
, 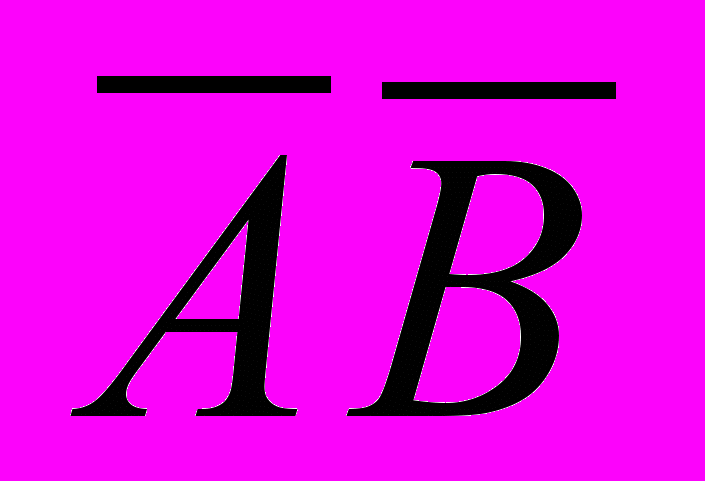 =
= ,
, 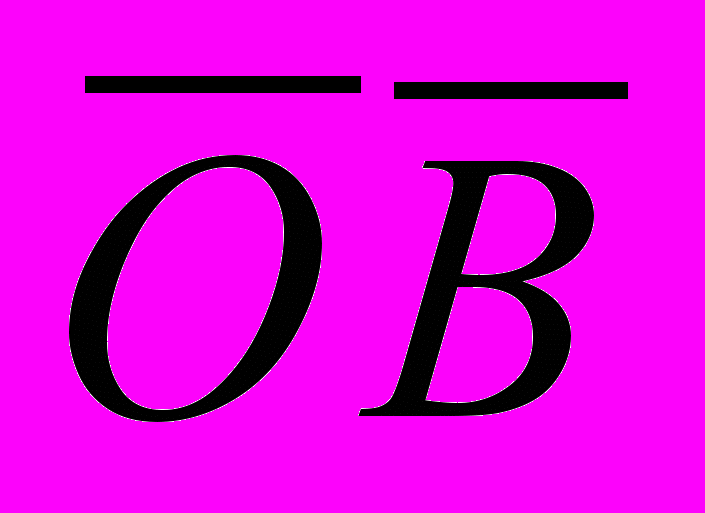 =
= +
+ ,
,  =
= и
и 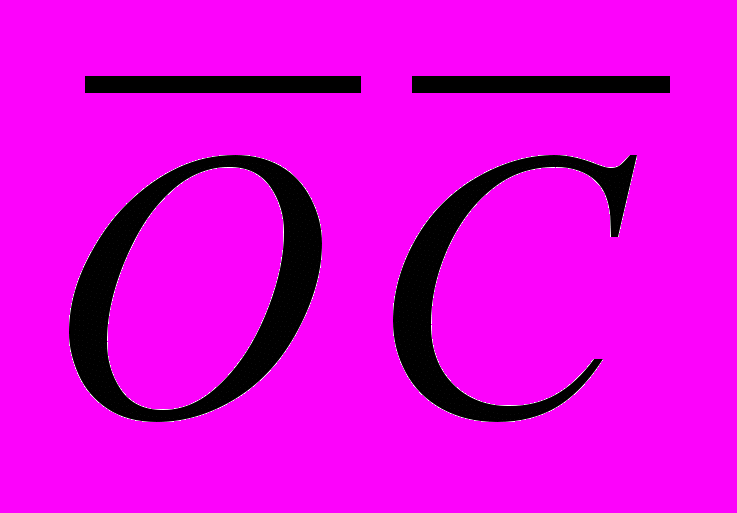 =
=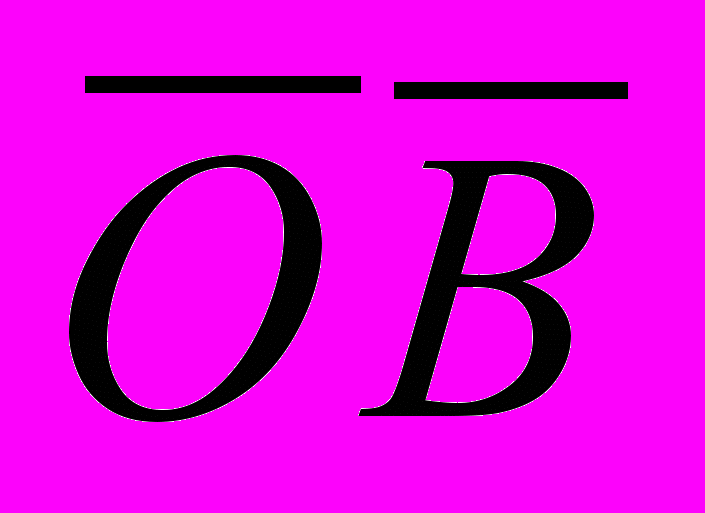 +
+ =(
=( +
+ )+
)+
В
С
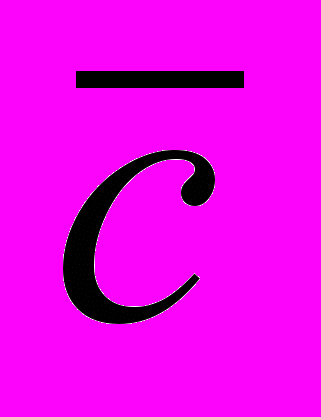
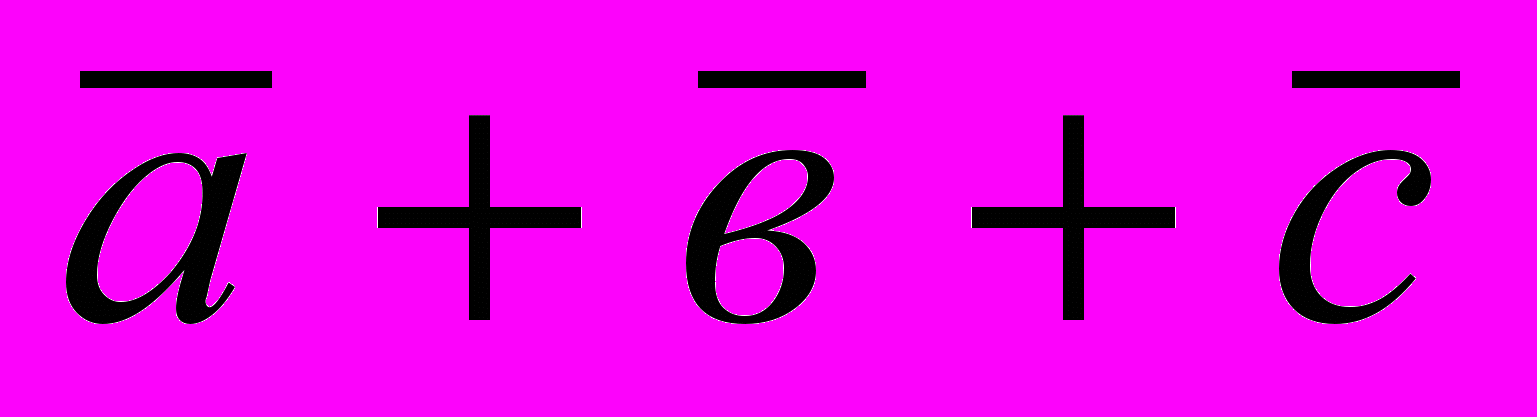
Из рисунка видно, что тот же вектор
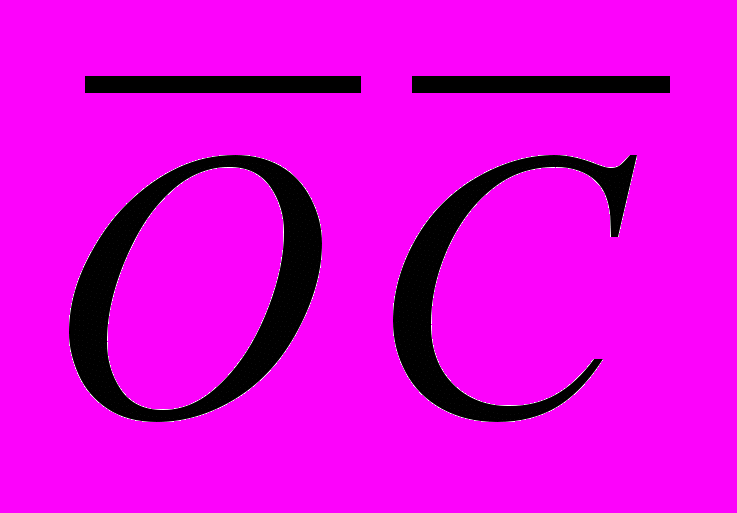 мы получим, если к вектору
мы получим, если к вектору 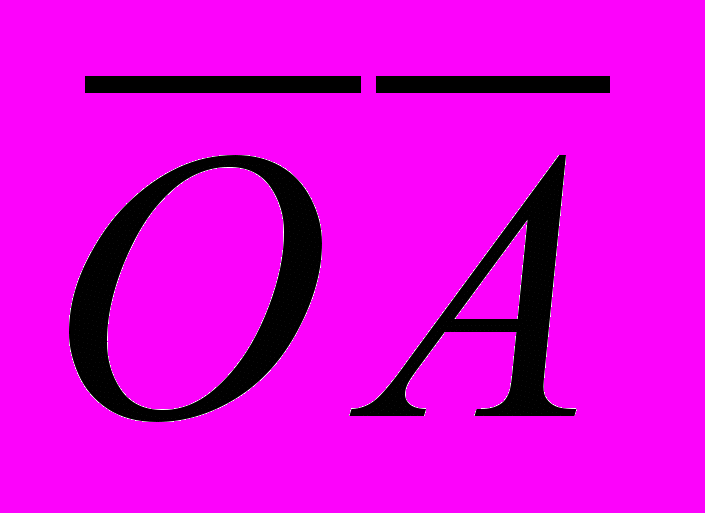 =
= прибавим вектор
прибавим вектор 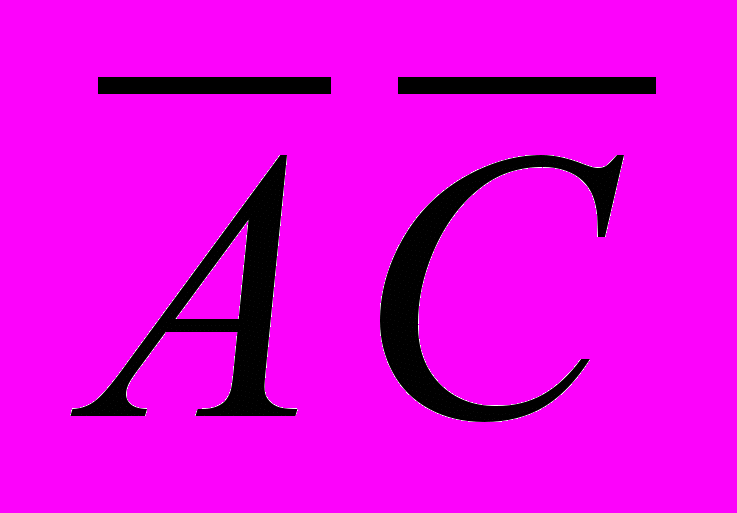 =
= +
+ .Таким образом, (
.Таким образом, ( +
+ )+
)+ =
= +(
+( +
+ ), т.е. сумма векторов обладает сочетательным свойством. Поэтому сумму трёх векторов
), т.е. сумма векторов обладает сочетательным свойством. Поэтому сумму трёх векторов  ,
,  и
и  записывают просто
записывают просто  +
+ +
+ .
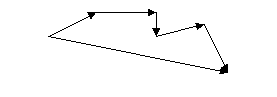
.Аналогично можно построить сумму четырёх, пяти и вообще любого числа векторов. Это правило построения суммы нескольких векторов называется «правилом многоугольника».
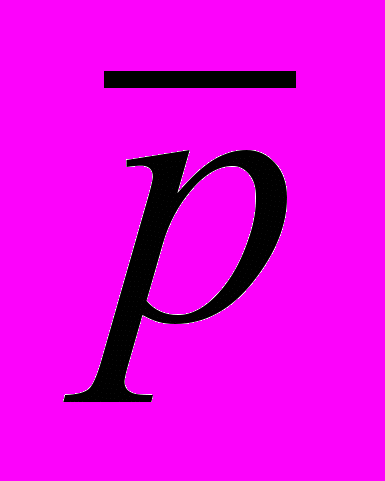 =
= +
+ +
+ +
+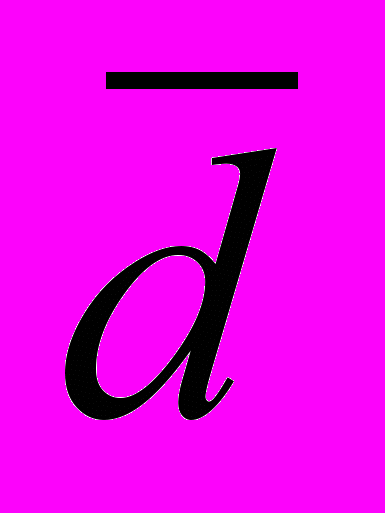 +
+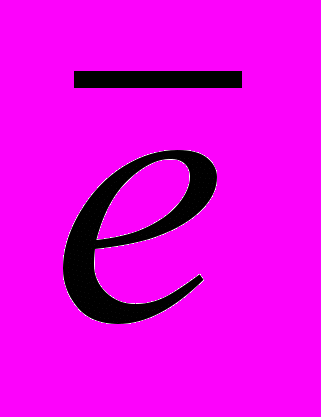
Из произвольной точки О откладывается вектор, равный первому слагаемому вектору. К концу первого вектора присоединяется начало второго; к концу второго – начало третьего и т.д. Вектор, соединяющий начало первого вектора с концом последнего, является суммой данных векторов.
Если при сложении нескольких векторов конец последнего слагаемого вектора совпадает с началом первого, то сумма векторов равна нулевому вектору. Очевидно, что для любого вектора имеет место равенство
 +0=
+0= .
.- Разность векторов
Разностью векторов
 и
и  называется такой вектор
называется такой вектор  =
= -
-  , сумма которого с вычитаемым вектором
, сумма которого с вычитаемым вектором  дает вектор
дает вектор  . Таким образом, если
. Таким образом, если  =
= -
-  , то
, то  +
+ =
= .
.Разность векторов
 и
и  обозначается так:
обозначается так:  -
-  .
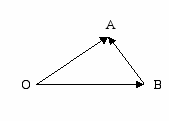
.Из определения суммы двух векторов вытекает правило построения вектора – разности. Откладываем векторы
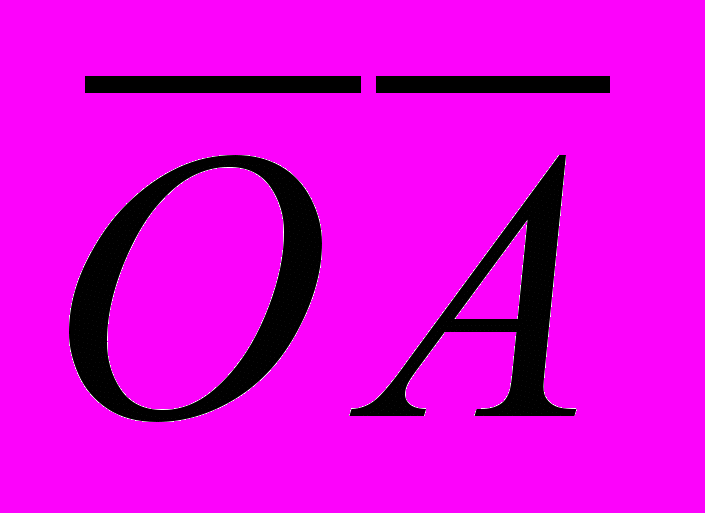 =
= и
и 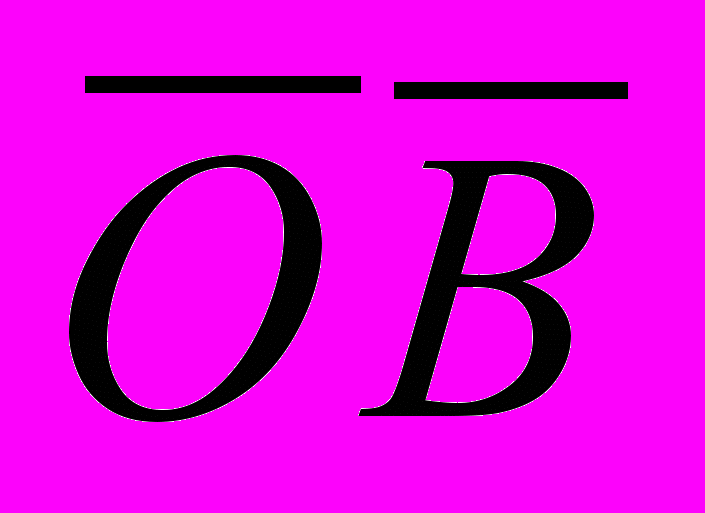 =
= из общей точки О. Вектор
из общей точки О. Вектор 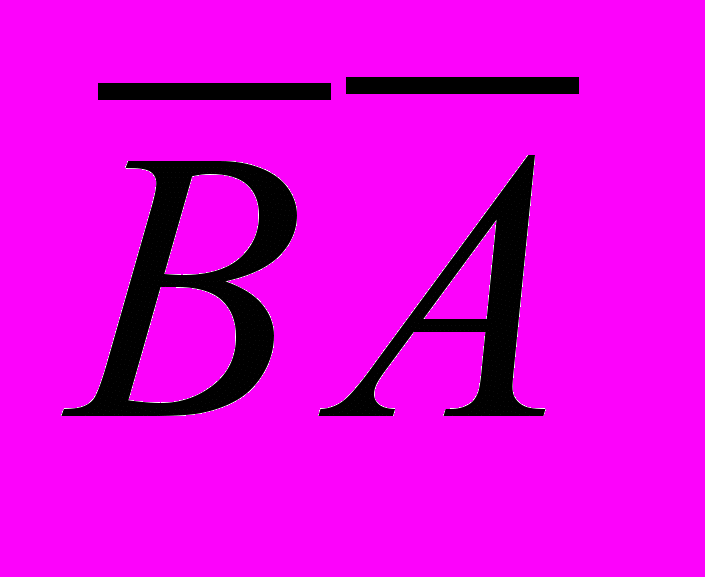 , соединяющий концы уменьшаемого вектора
, соединяющий концы уменьшаемого вектора  и вычитаемого вектора
и вычитаемого вектора  , является разностью
, является разностью  =
= -
-  . Действительно, по правилу сложения векторов
. Действительно, по правилу сложения векторов 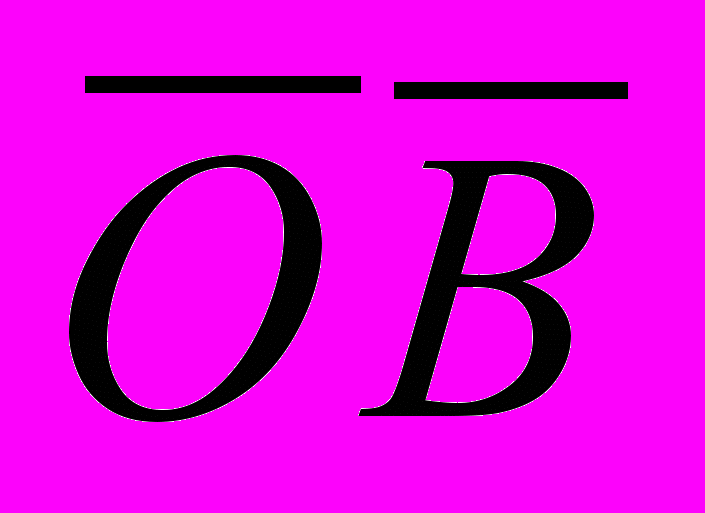 +
+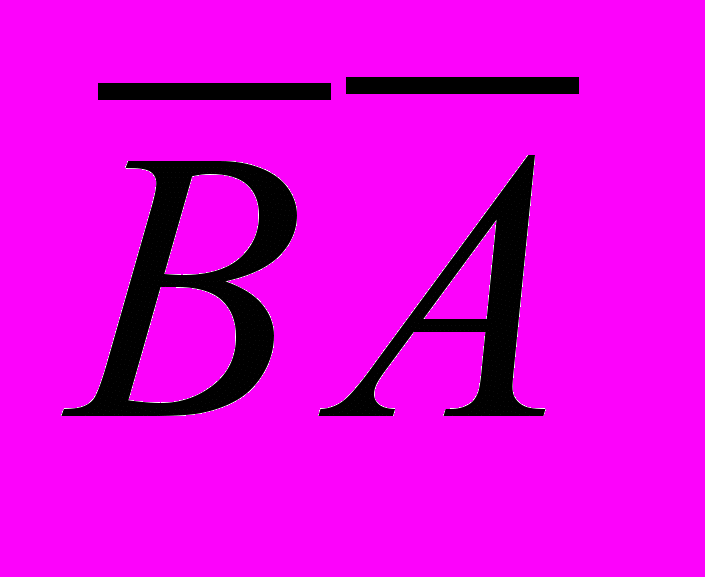 =
=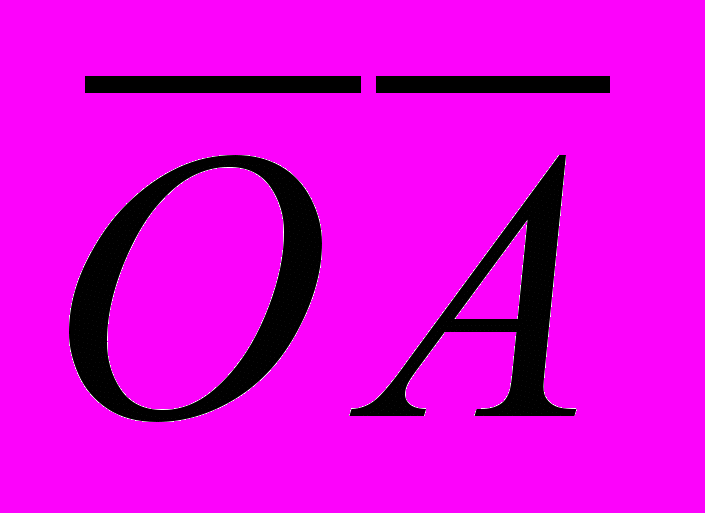 , или
, или  +
+ =
= .
.
Задачу о построении разности двух векторов можно решить и другим способом.
Пусть даны векторы
 и
и  справедливо равенство
справедливо равенство  -
- =
= +(-
+(- ).
).Вектор -
 называется противоположным вектору
называется противоположным вектору  , если вектор
, если вектор  и -
и - имеют равные длины и противоположно направлены.
имеют равные длины и противоположно направлены.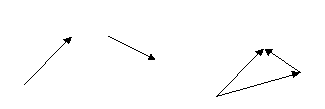
Вектором, противоположным нулевому вектору, считается нулевой вектор.
Если -
 противоположный вектору
противоположный вектору  , то, очевидно,
, то, очевидно,  +(-
+(- )= 0
)= 0- Произведение вектора на число.
Произведением ненулевого вектора
 и
и  на число k называется такой вектор
на число k называется такой вектор  , длина которого равна
, длина которого равна 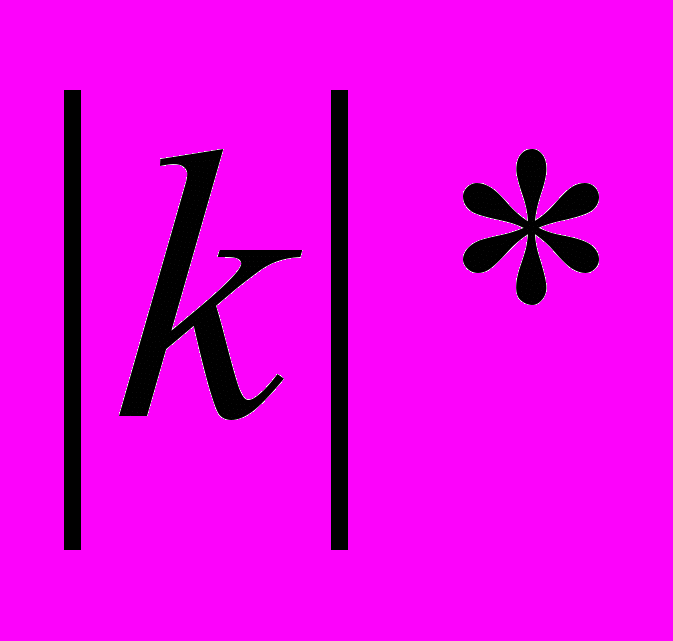
 , причем векторы
, причем векторы  и
и  соноправлены при k>=0 и противоположно направлены при k<0. Произведением ненулевого вектора на любое число считается ненулевой вектор.
соноправлены при k>=0 и противоположно направлены при k<0. Произведением ненулевого вектора на любое число считается ненулевой вектор.Произведение вектора
 на число k обозначается так: k*
на число k обозначается так: k* .
.Н

а рисунке изображены вектор
 и векторы 3*
и векторы 3* , -1,5*
, -1,5* .
.
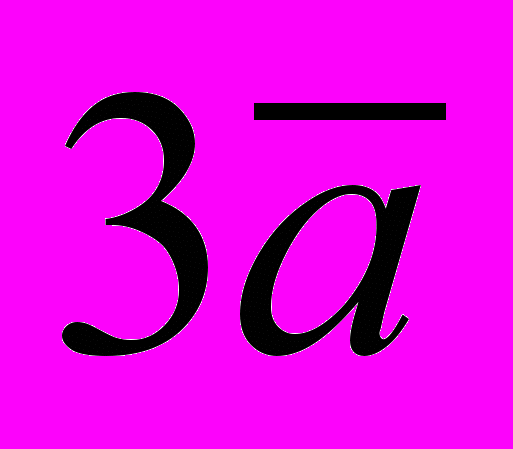
Из определения произведения вектора на число непосредственно следует, что:
- произведение любого вектора на число нуль есть нулевой вектор;
- для любого числа k и любого вектора
 векторы
векторы  и k*
и k* коллинеарны
коллинеарны
Умножение вектора на число обладает следующими основными свойствами (для любых чисел k, l и любых векторов
 ,
,  ) :
) :- (k*l)*
 =k*(l*
=k*(l* )-сочетательный закон
)-сочетательный закон
- (k+l)*
 =k*
=k* +l*
+l*
- k*(
 +
+ )=k*
)=k* +k*
+k*
Заключение
В данном реферате показано широкое применение векторного аппарата, использование вектора при решении задач.
Реферат способствует расширению знаний учащихся, развитию и формированию мыслительных операций.
В данном реферате были поставлены и рассмотрены цели изучения векторного метода в школе. С помощью поставленных целей мы познакомились с историей возникновения векторного исчисления, с понятием вектор, рассмотрели понятийный аппарат векторного метода решения задач, выделены основные компоненты решения задач этого метода.
Реферат помог научиться решать простейшие задачи с помощью построения векторов. Примеры этих задач взяты и подробно разобраны только из школьной программы. При решении задач были использованы различные линейные операции, такие как сумма и вычитание векторов, умножение вектора на число.
Для формирования метода в реферате были представлены основные этапы: подготовительный, мотивационный, этап овладении компонентами метода, этап формирования метода «в целом».
Этот материал может быть интересен и полезен для учителя при использовании векторного метода при решении задач с целью форматирования у учащихся выполнять обобщение и конкретизацию.
Список литературы
1. Мантуров О. В., Матвеев Н. М. Курс высшей математики. – М.: Высшая школа, 1986. – 480 с.
2. Александров П. С. Курс аналитической геометрии и линейной алгебры. – М.: Наука, Гл. ред. физ.-мат. лит., 1979. – 512 с.
3. Базылев В. Т., Дуничев К. И., Иваницкая В. П. Геометрия. ч. 1.- М.: Просвещение, 1974. – 352 с.
4. Атанасян Л. С., Базылев В. Т., Геометрия. ч. 1. – М.: Просвещение, 1986. – 336 с.
5. Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры.– 4-е изд. – М.: Наука. Гл. ред. физ.-мат. лит., 1980. – 336 с.
6. Простников М. М. Лекции по геометрии. Семестр I. Аналитическая геометрия. – М.: Наука, Гл. ред. физ.-мат. лит., 1986. – 416 с.
7. Кострикин А. И., Манин Ю. И. Линейная алгебра и геометрия. – М.: Наука, Гл. ред. физ.-мат. лит., 1986. – 304 с.
8. Простников М. М. Лекции по геометрии. Семестр III. Линейная алгебра. – М.: Наука, Гл. ред. физ.-мат. лит., 1986. – 400 с.
Перейти к оглавлению
