Урок математики с информатикой по теме «Иррациональные уравнения и неравенства»
| Вид материала | Урок |
- Тема: «Рациональные и иррациональные уравнения, неравенства и системы», 199.57kb.
- Блочно-модульное обучение: из опыта работы. Урок математики, 11-й класс. Иррациональные, 157.76kb.
- П. В. Чулков, «Уравнения и неравенства в школьном курсе математики, лекции 1-4», стр, 8.44kb.
- Урок по алгебре и началам анализа в 10г классе учителя математики моу «сош №32 г. Энгельса», 97.37kb.
- Урок математики в 6 классе по теме «Решение задач на составление уравнений», 98.1kb.
- Программа элективного курса Показательные, логарифмические, иррациональные уравнения, 113.96kb.
- Тема «Иррациональные уравнения и неравенства» введение, 223.72kb.
- Урок по теме: "Показательные функции, уравнения, неравенства", 69.08kb.
- Элективный курс по математике для учащихся 9 класса тема: «уравнения и неравенства,, 248.15kb.
- Поурочное планирование (5 часов в неделю, всего 170 часов) Тема, 155.46kb.
Интегрированный урок математики с информатикой по теме «Иррациональные уравнения и неравенства»
(11физико-математический класс, обобщающий урок, учебник А.Г.Мордкович «Алгебра и начала анализа 10-11 )
Цели урока:
- познакомить учащихся с историей жизни и математической деятельности известных учёных-математиков Ф.Виета, Э.Галуа, К.Ф.Гаусса
- повторить теоремы для решения иррациональных неравенств
- познакомить учащихся с нестандартными приёмами решения иррациональных уравнений и неравенств
- провести самостоятельную работу с оформлением решения, используя редактор формул
Оборудование: компьютер, проектор, индивидуальные задания для самостоятельной работы
План урока.
- Вступительное слово учителя.
- Исторические справки о жизни и деятельности учёных-математиков
- Сообщение с презентацией по теме «Иррациональные неравенства» (Презентация 1)
- Сообщение с презентацией по теме «Нестандартные методы решения иррациональных уравнений и неравенств» (Презентация 2)
- Самостоятельная работа с выводом решения на печать
- Итоги урока
Ход урока
Вступительное слово учителя: «Народная мудрость гласит, что, не зная прошлого, невозможно понять подлинный смысл настоящего и цель будущего. Это, конечно, относится и к математике» Поэтому мы сейчас познакомимся с некоторыми биографическими сведениями из жизни и математической деятельности учёных Франсуа Виета, Эвариста Галуа, Карла Фридриха Гаусса.
Учащиеся рассказывают, показывая презентации.
Нестандартные методы решения иррациональных уравнений и неравенств
- Скалярное произведение двух векторов
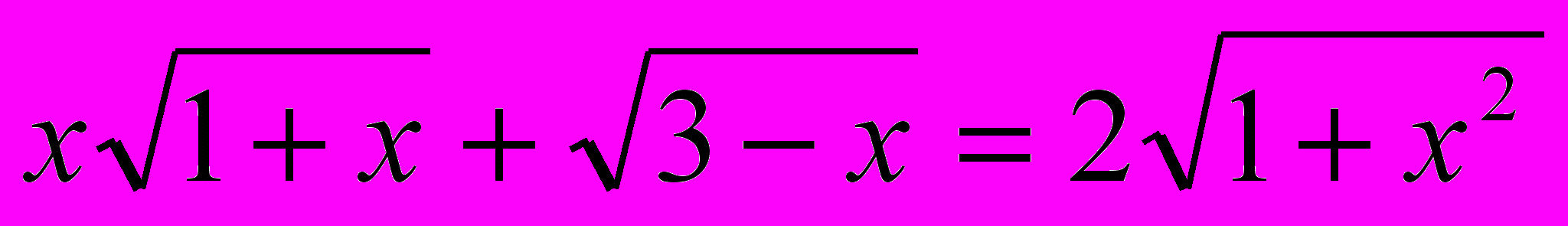
Введём два вектора так, чтобы левая часть уравнения представляла собой их скалярное произведение, а правая - произведение их длин (модулей):
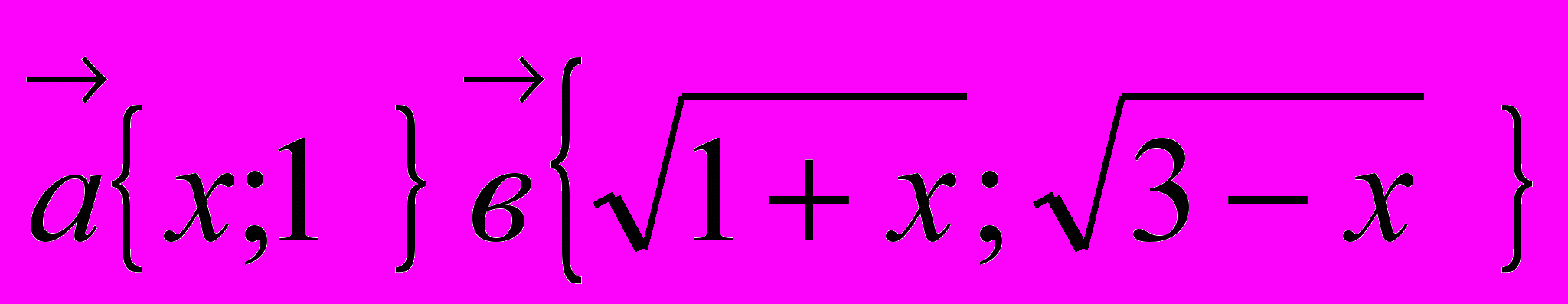 При этом
При этом 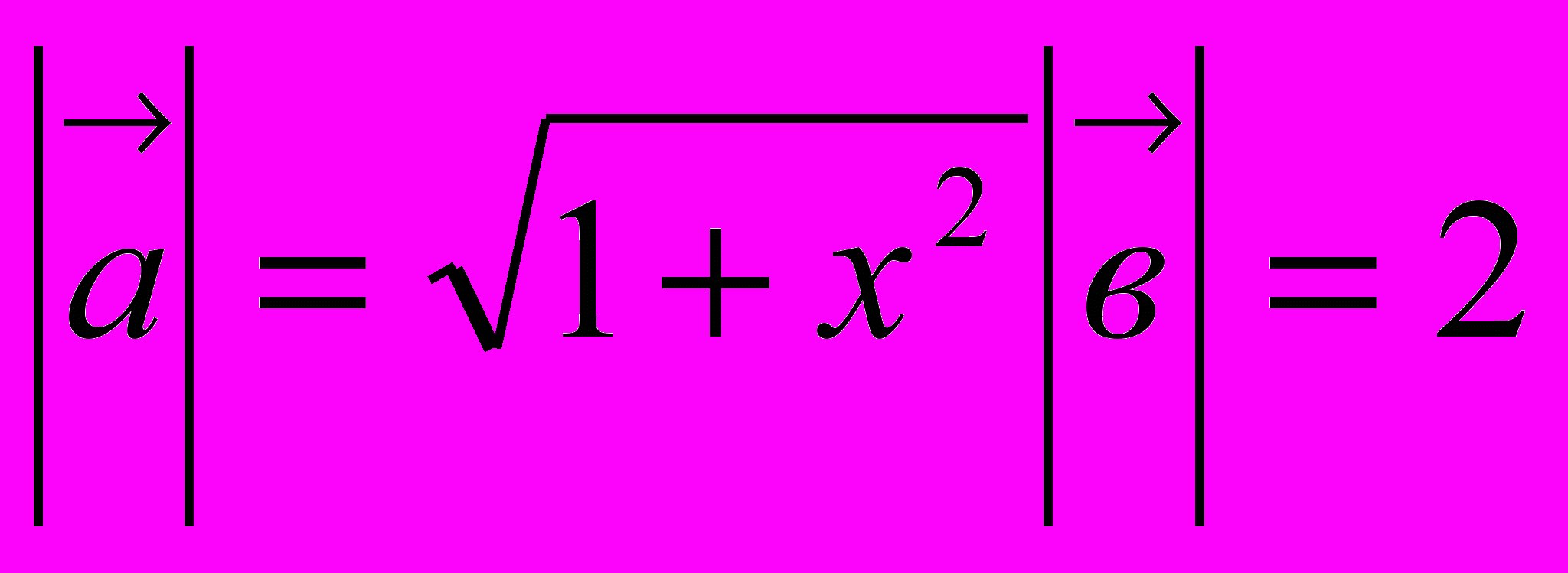
Скалярное произведение двух векторов равно произведению их длин в том и только том случае, если векторы сонаправлены. Два ненулевых вектора сонаправлены в том и только том случае, если отношения их соответственных координат равны одному и тому же положительному числу. Таким образом, исходное уравнение равносильно следующему:
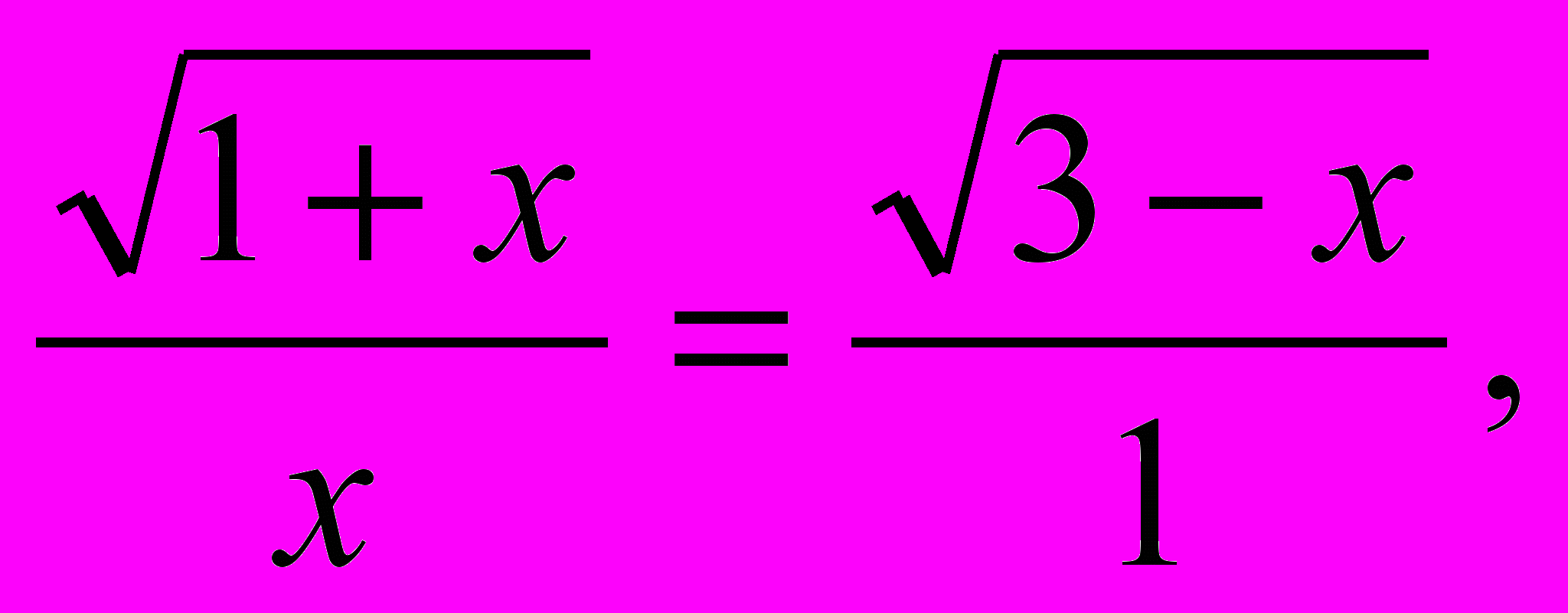 откуда х=1, х=1+
откуда х=1, х=1+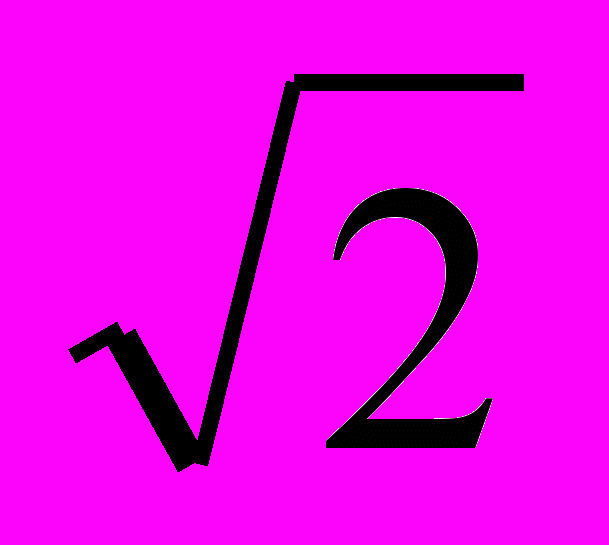 Ответ: х=1, х=1+
Ответ: х=1, х=1+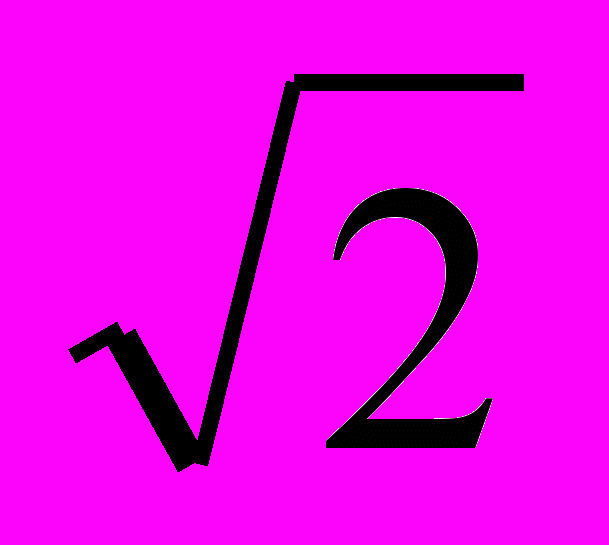
-
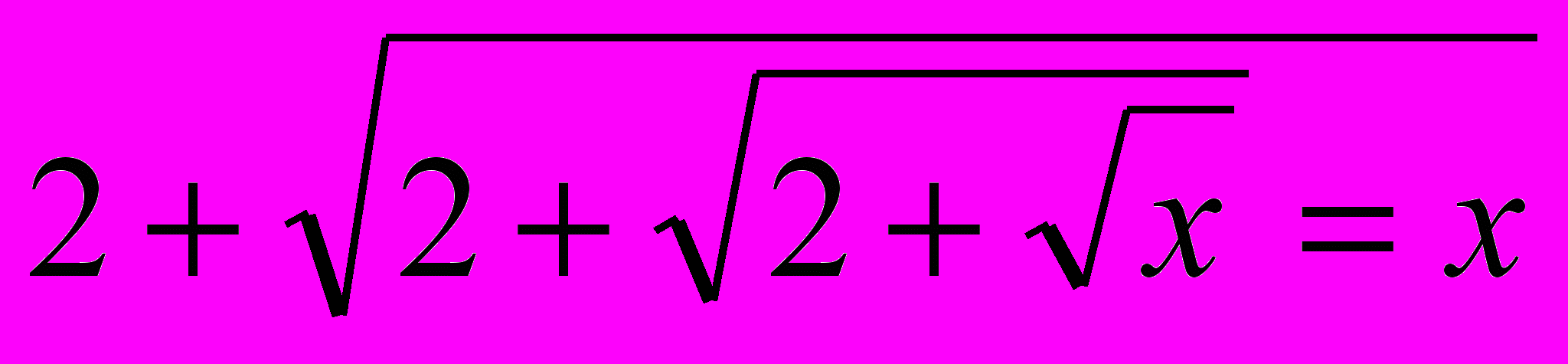 (Монотонность)
(Монотонность)
Рассмотрим f(х)=2+
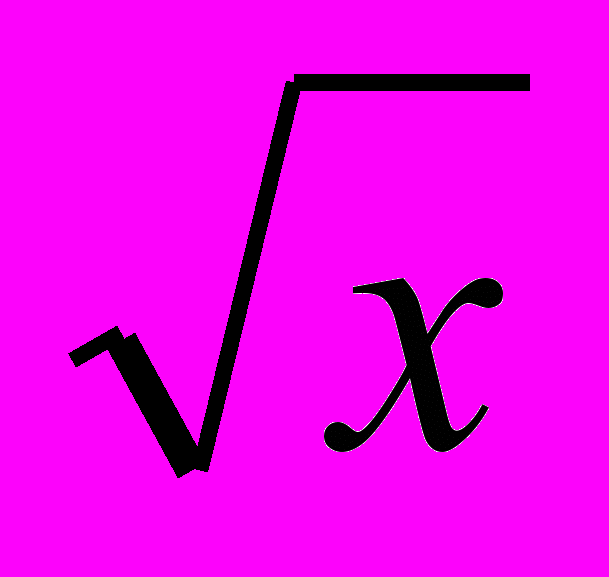 . Эта функция монотонно возрастает на D(f)=
. Эта функция монотонно возрастает на D(f)=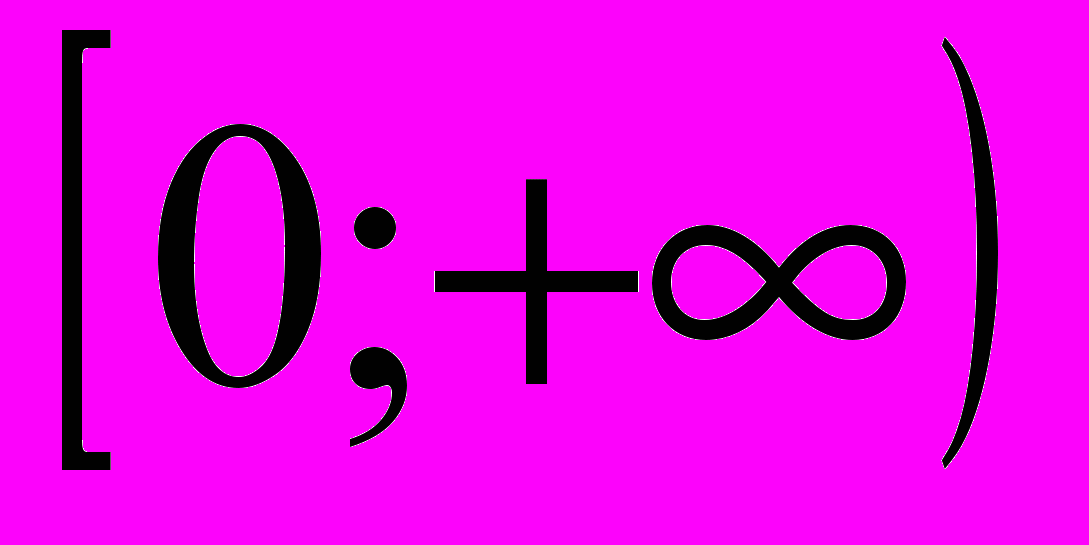
При этом исходное уравнение имеет вид: f(f(f(x)))=x. В силу возрастания функции оно равносильно уравнению f(x)=x, т.е. уравнению 2+
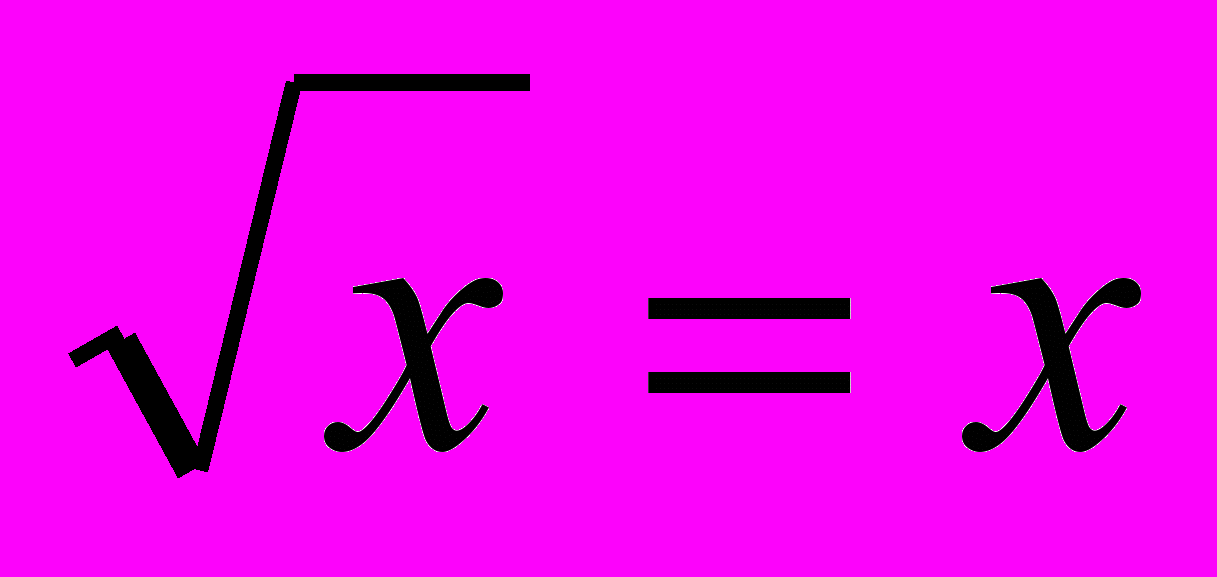
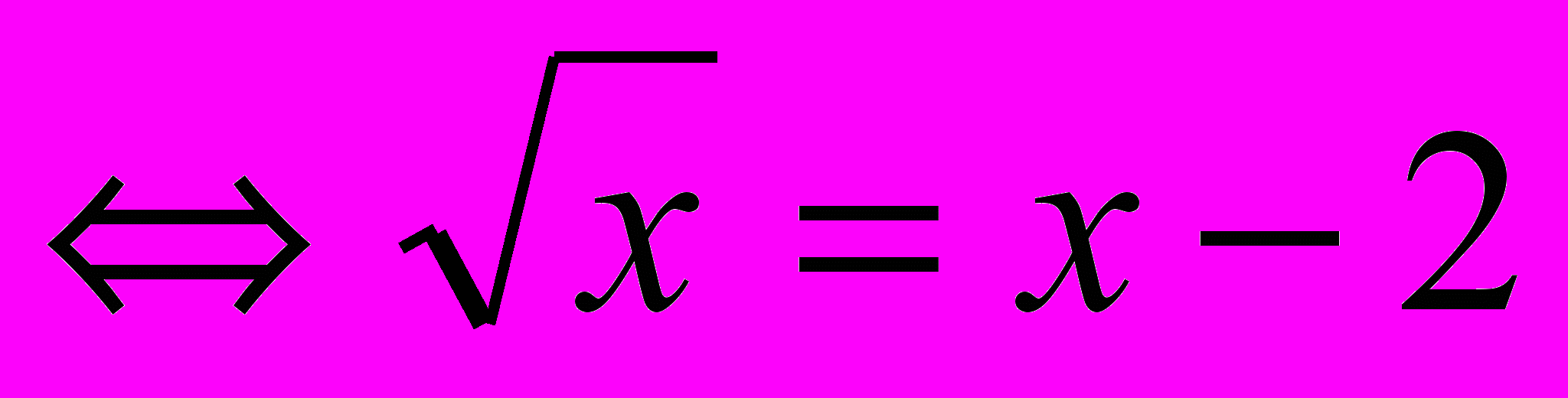
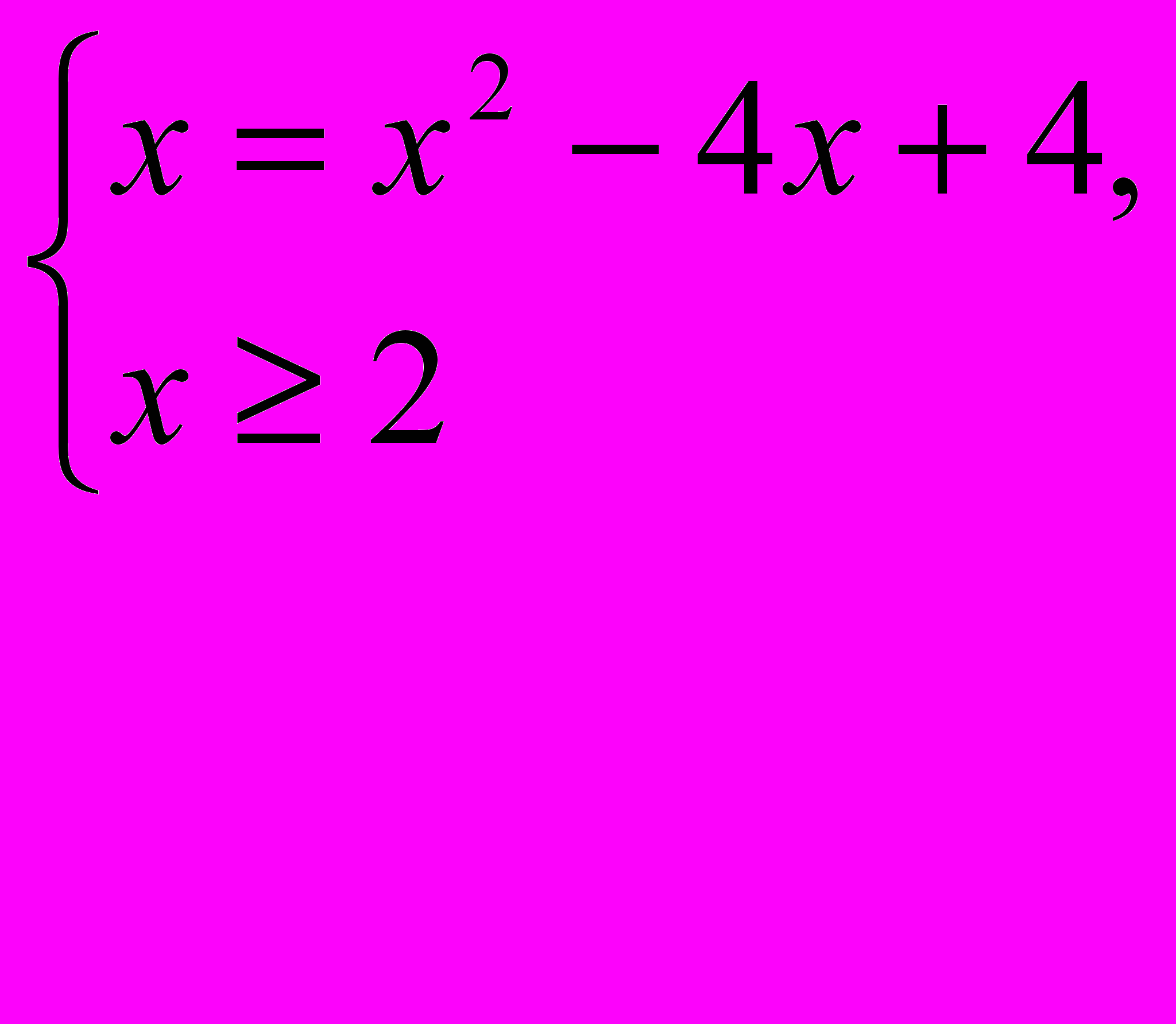
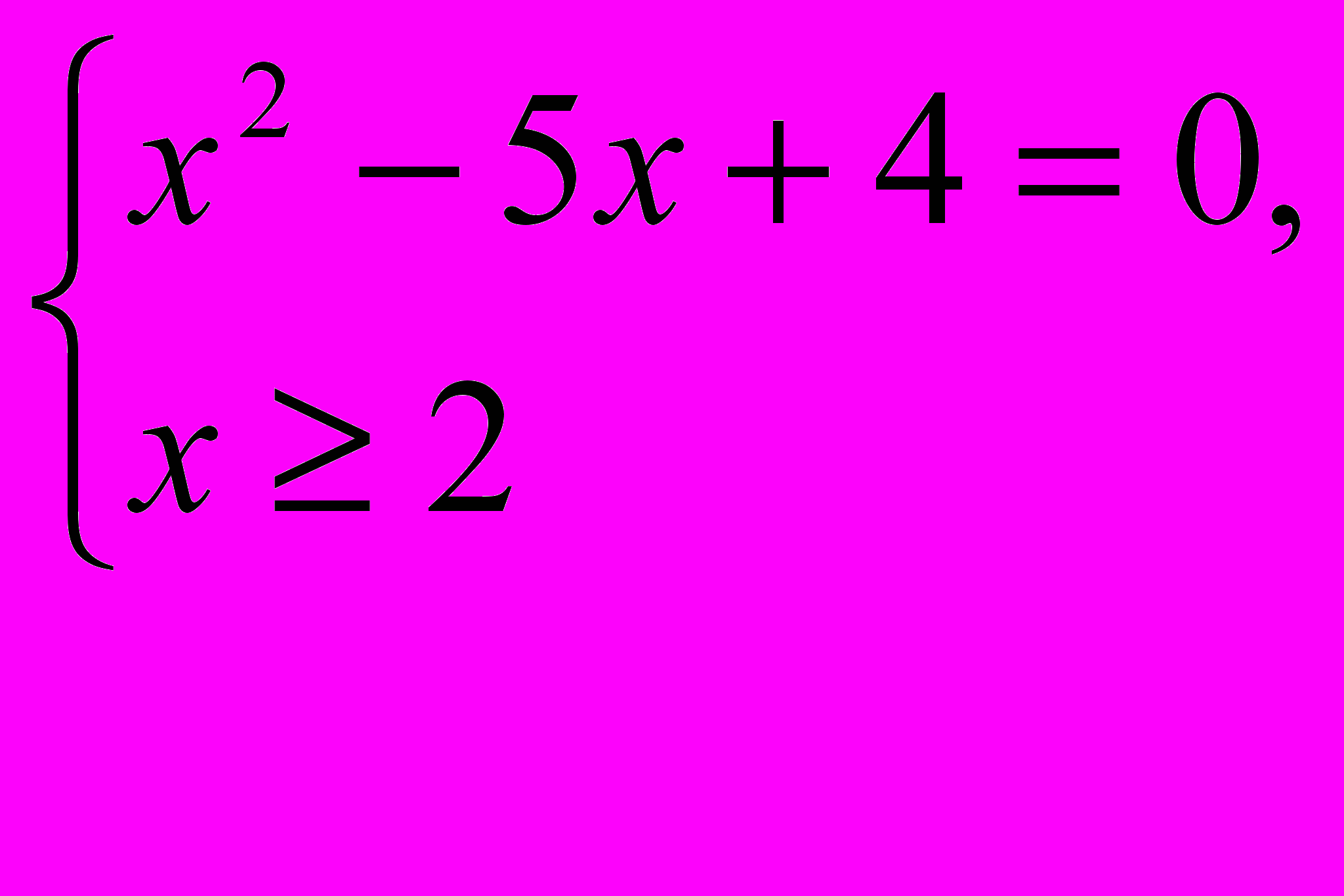
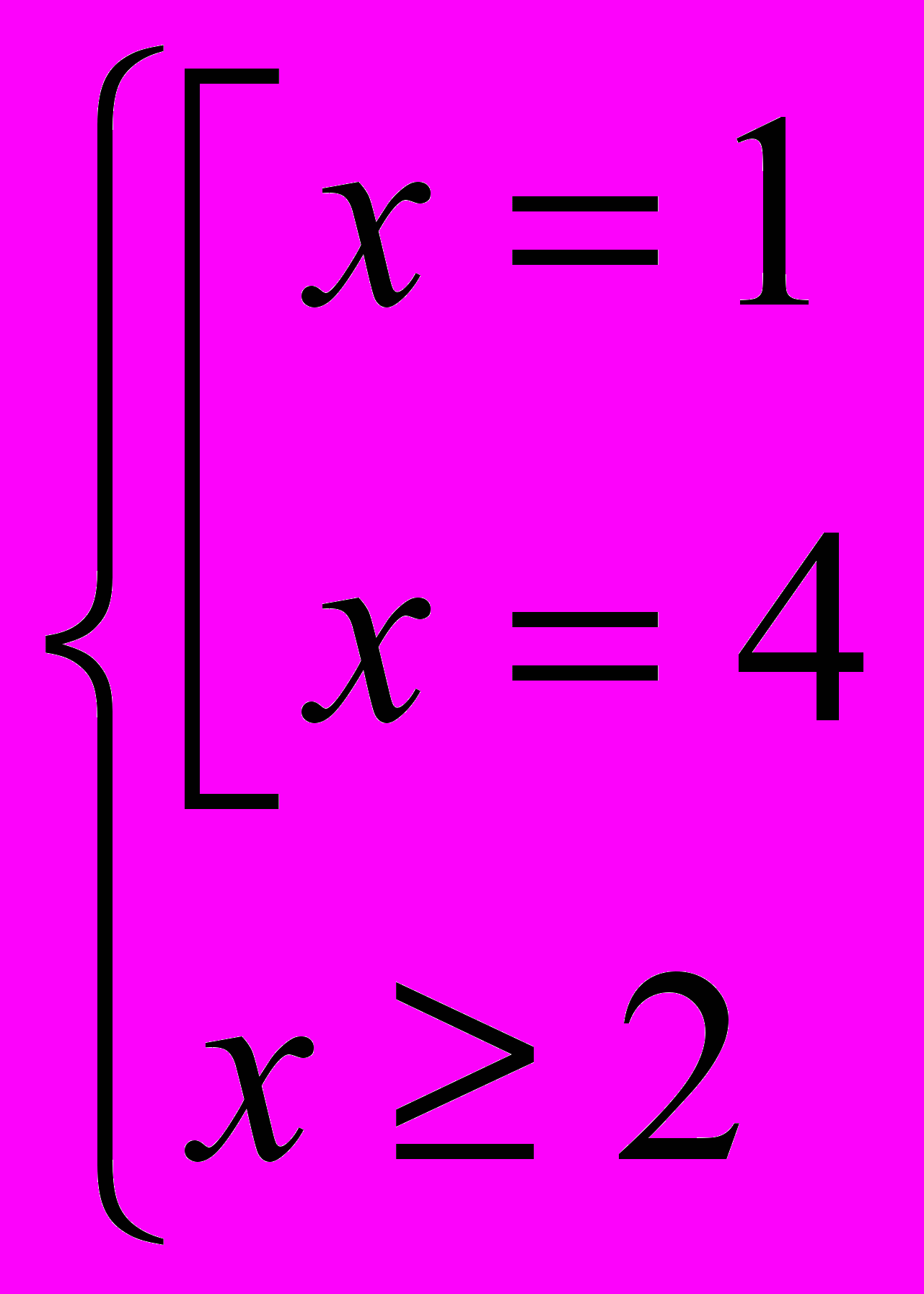
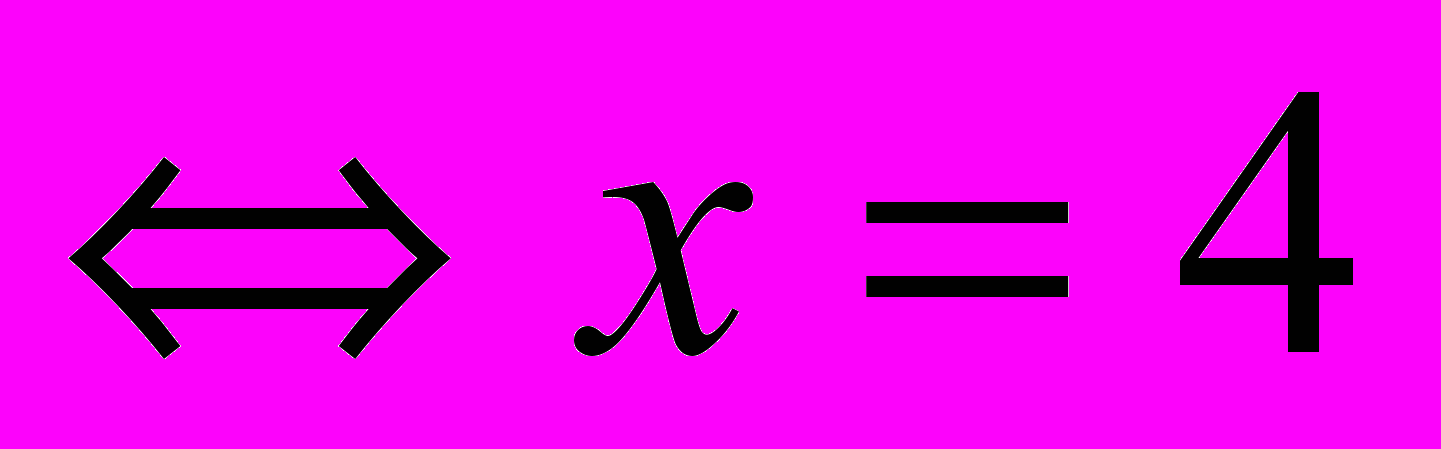
Ответ: х=4
3)
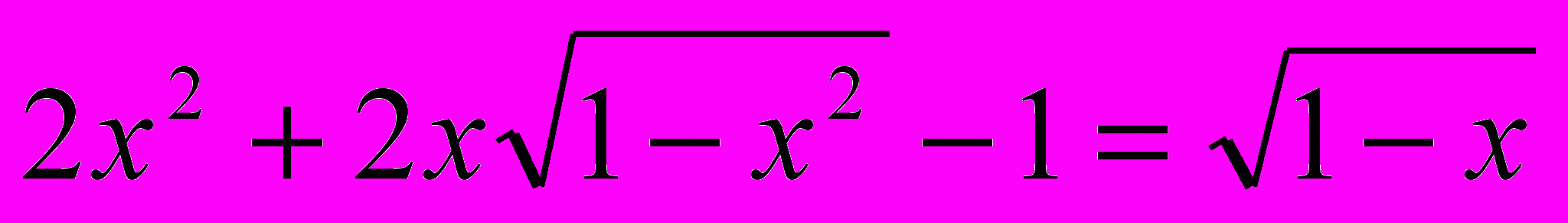 (Тригонометрическая подстановка)
(Тригонометрическая подстановка)Допустимые значения х должны удовлетворять неравенству:
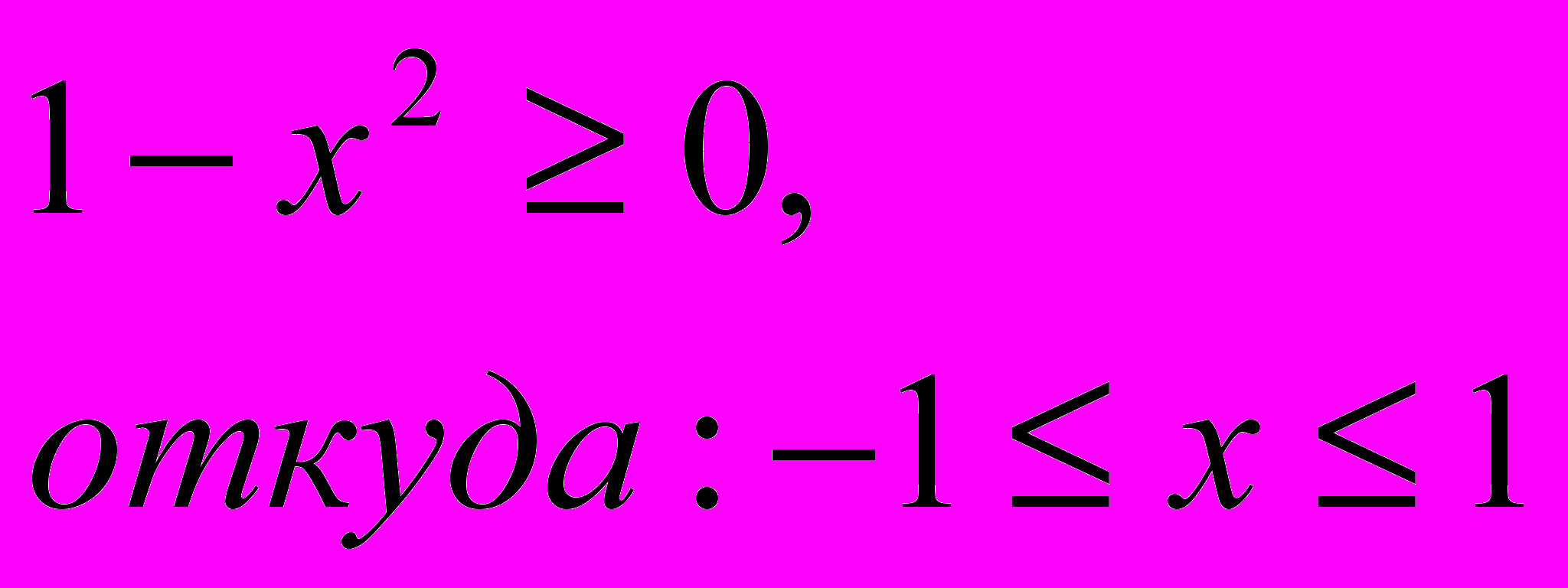
В силу ограничения на переменную х можно воспользоваться тригонометрической подстановкой: х = cos a, где
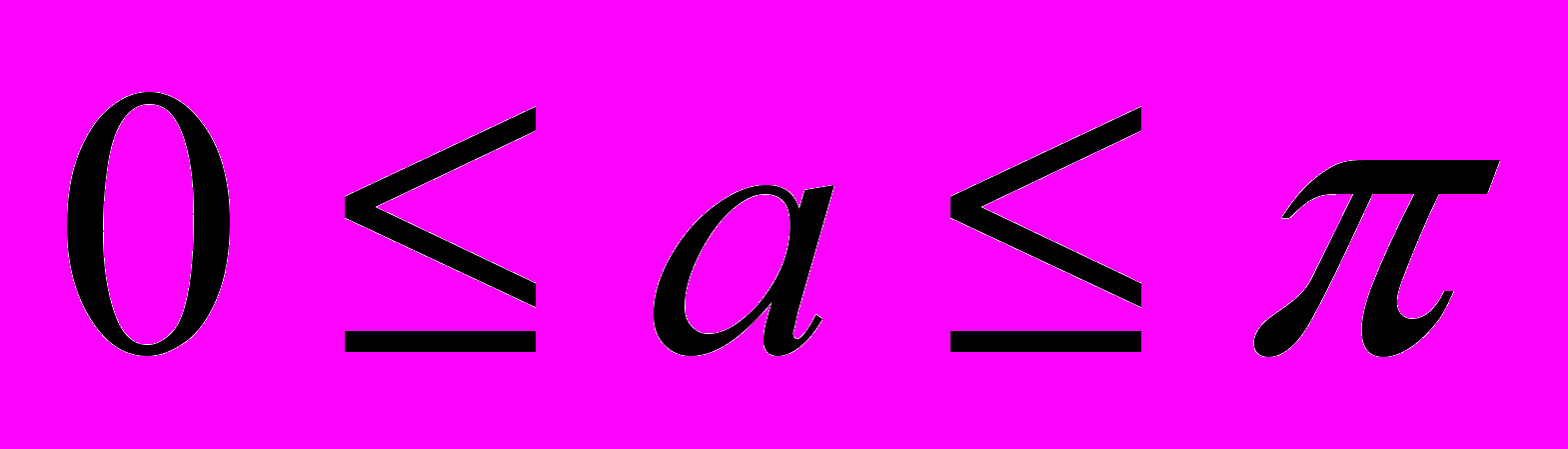 . В силу последнего неравенства sin a
. В силу последнего неравенства sin a 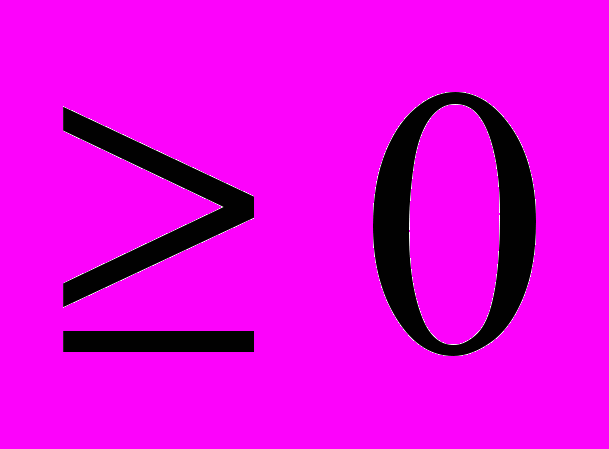 и
и 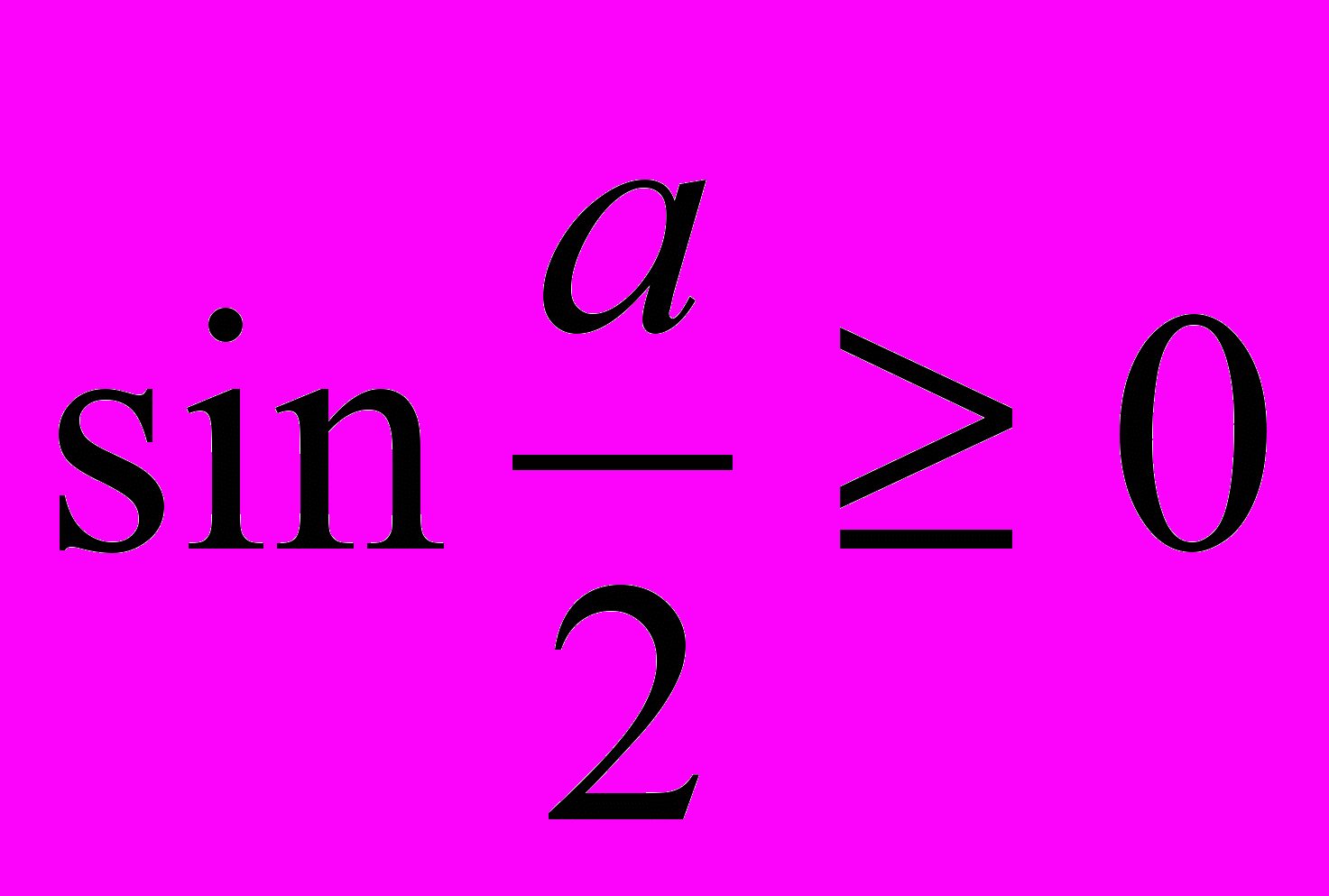
Поэтому:
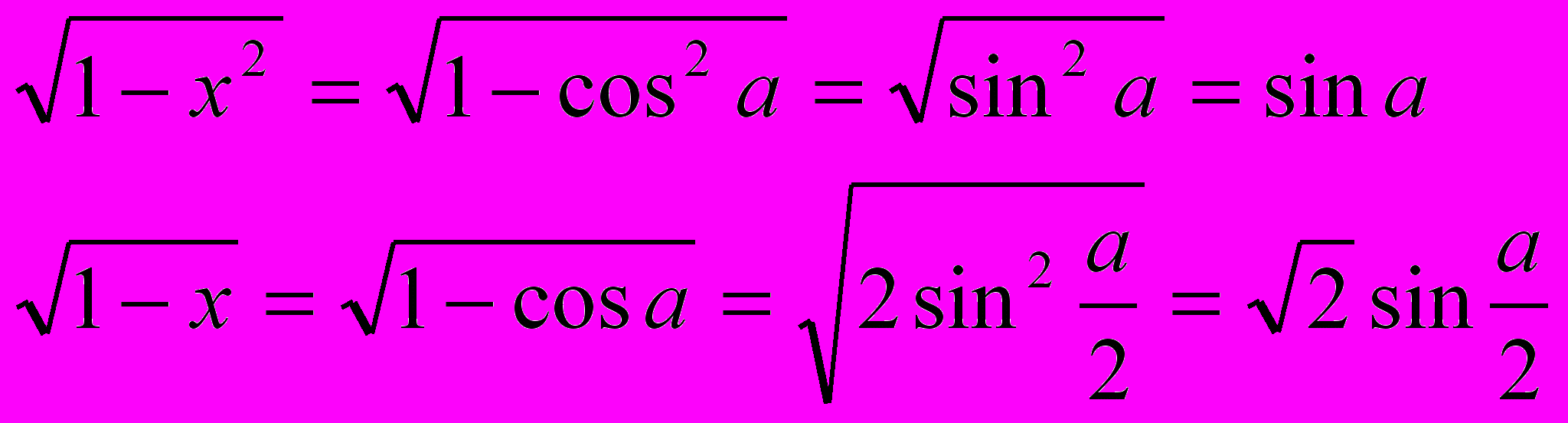
Таким образом уравнение примет вид:
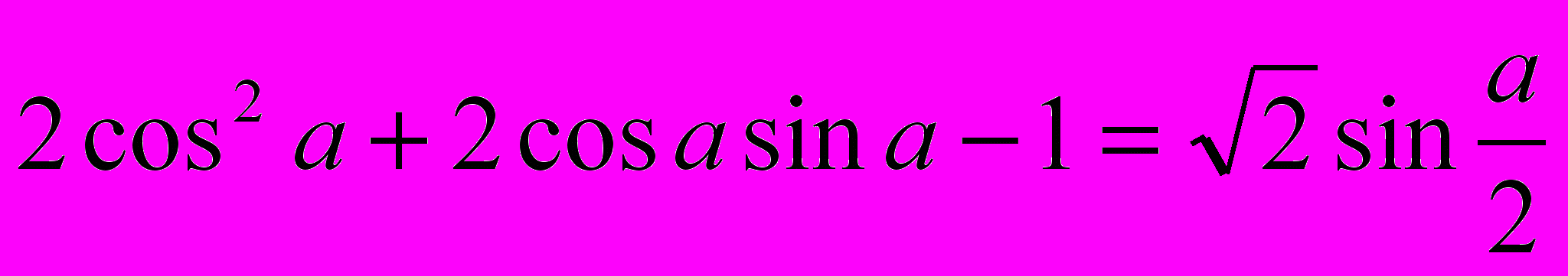
Решив уравнение, получим в силу неравенства
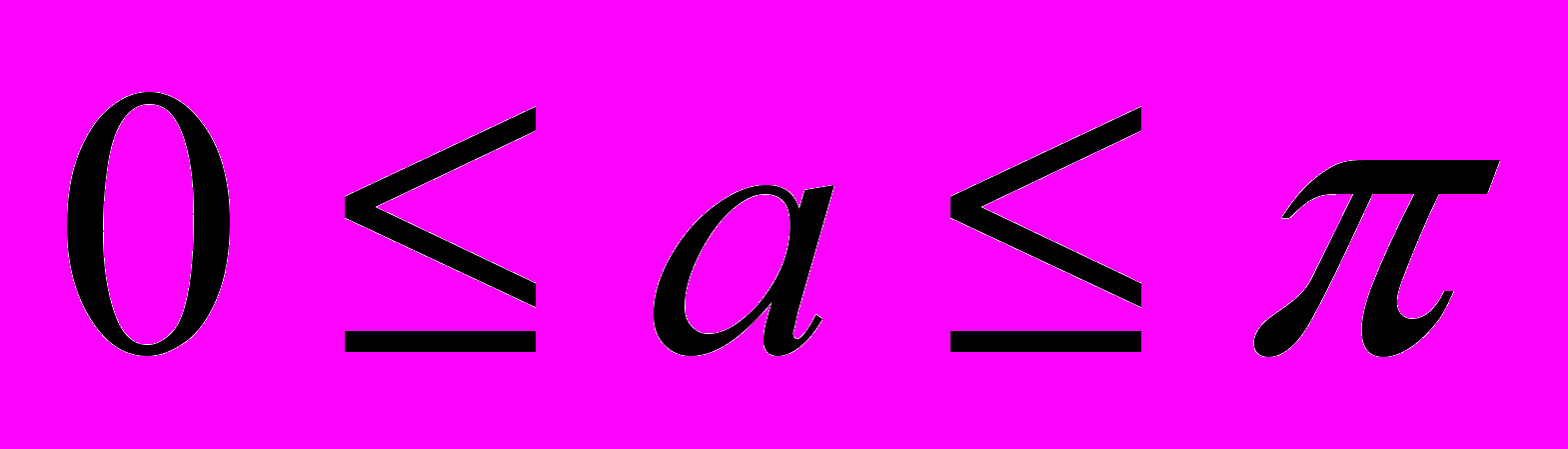 , что х=
, что х=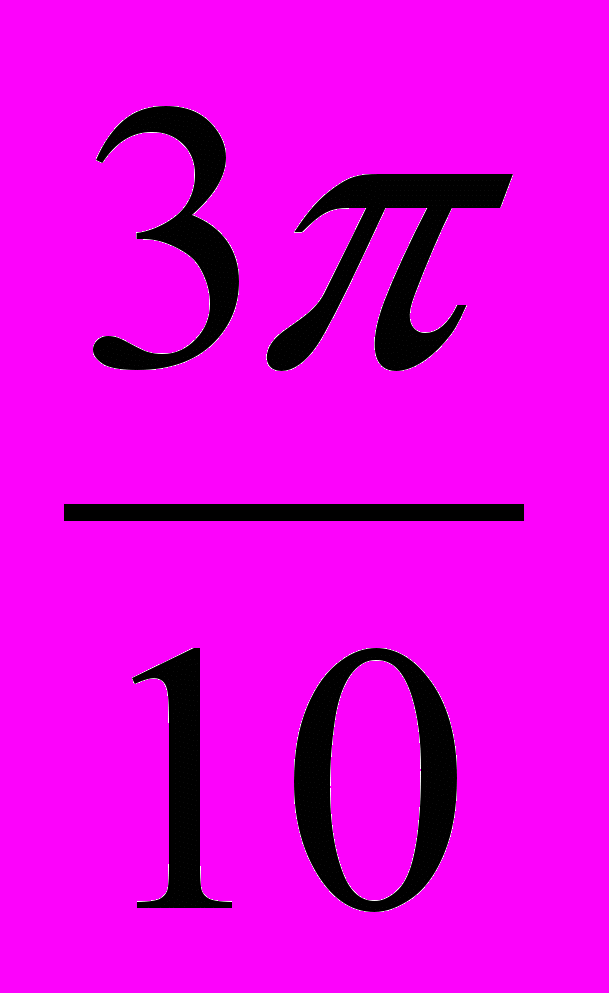
Cos2a+sin2a=
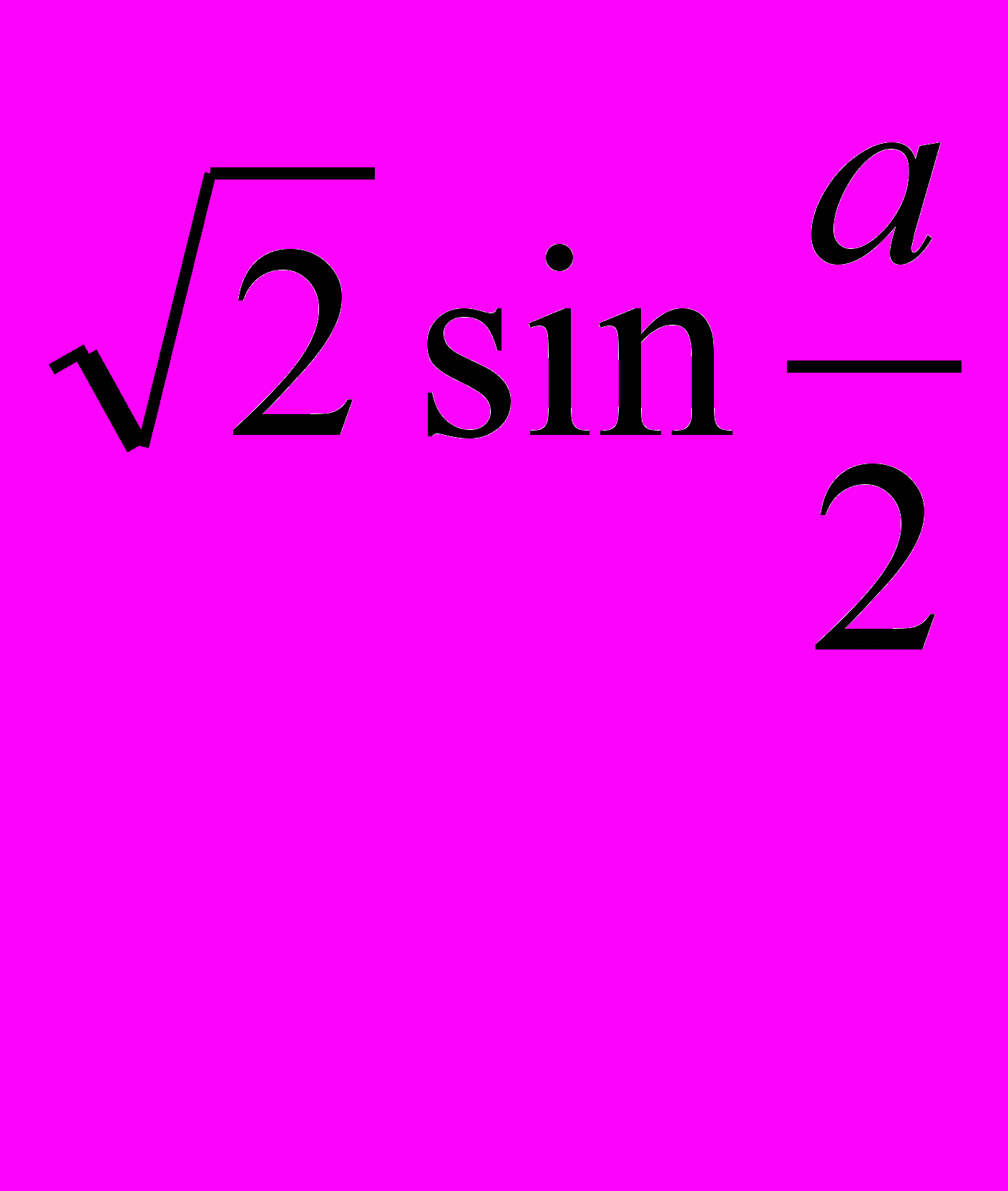
sin2a
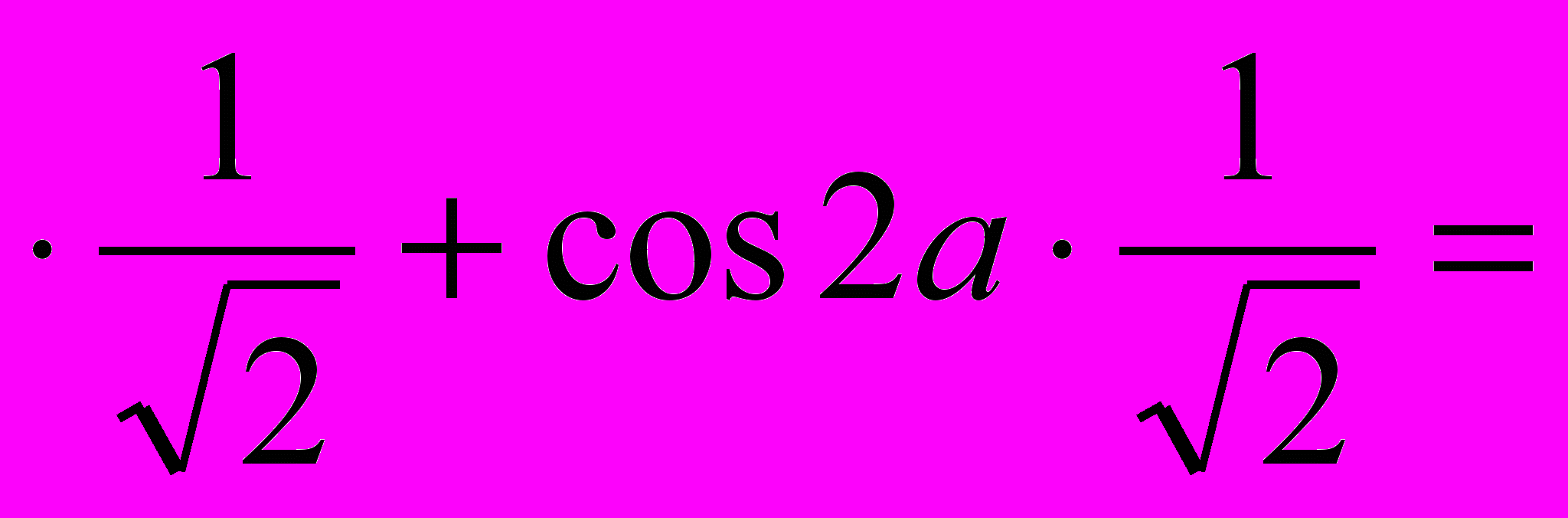 sin
sin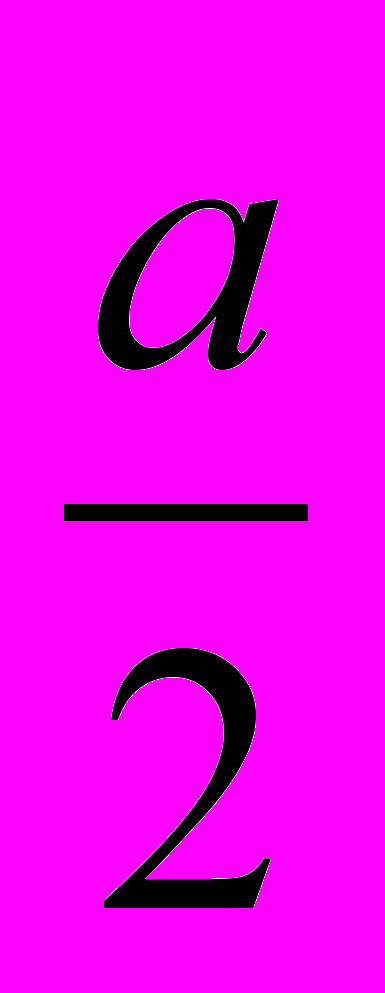 sin2a
sin2a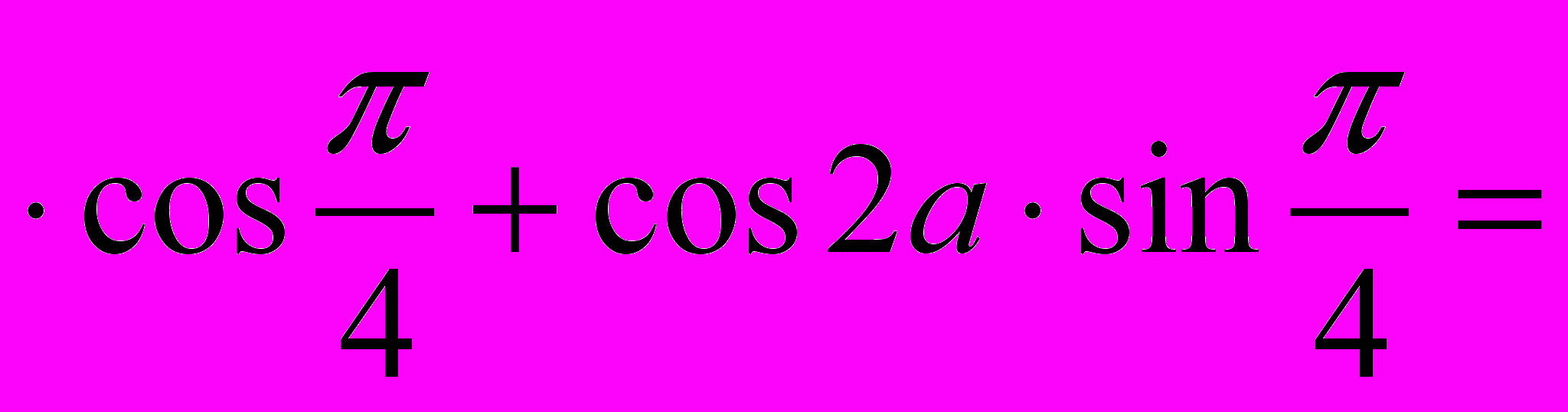 sin
sin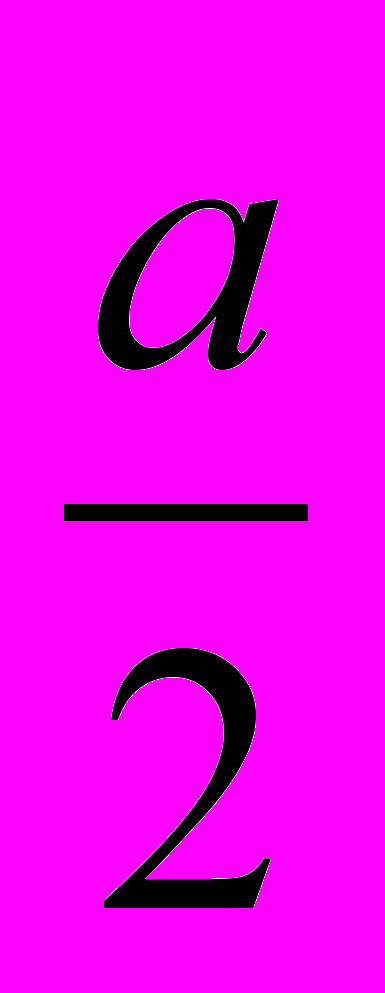
sin(2a+
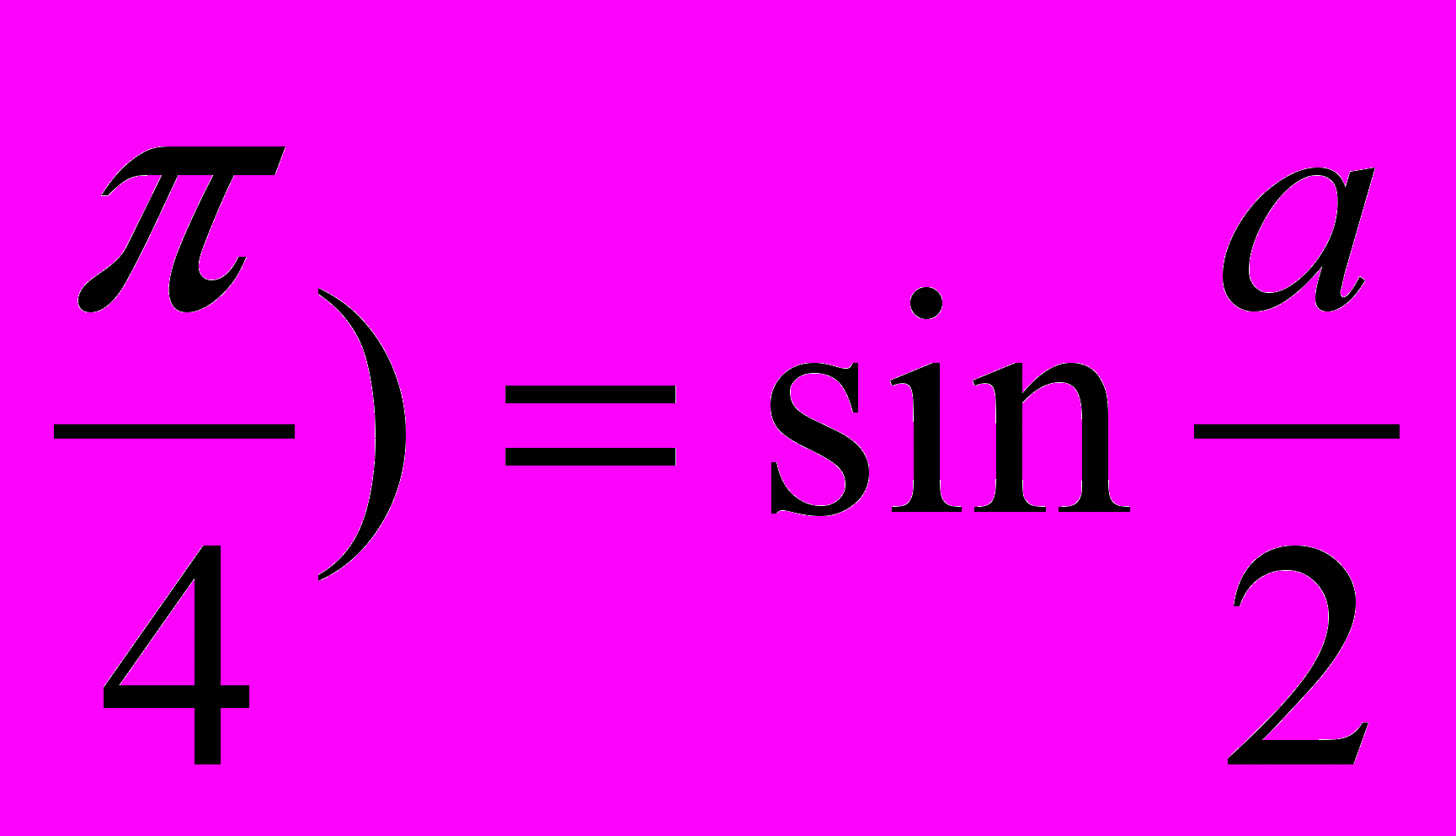
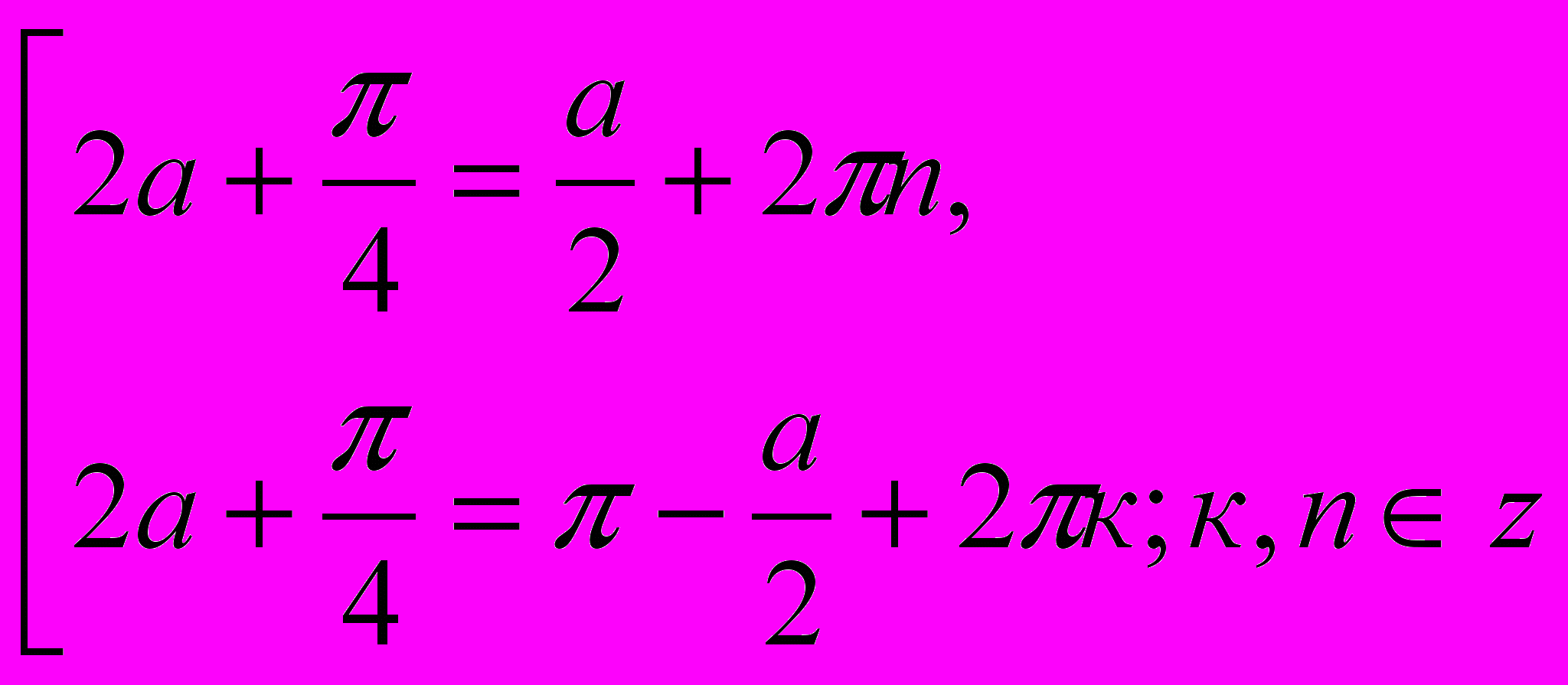
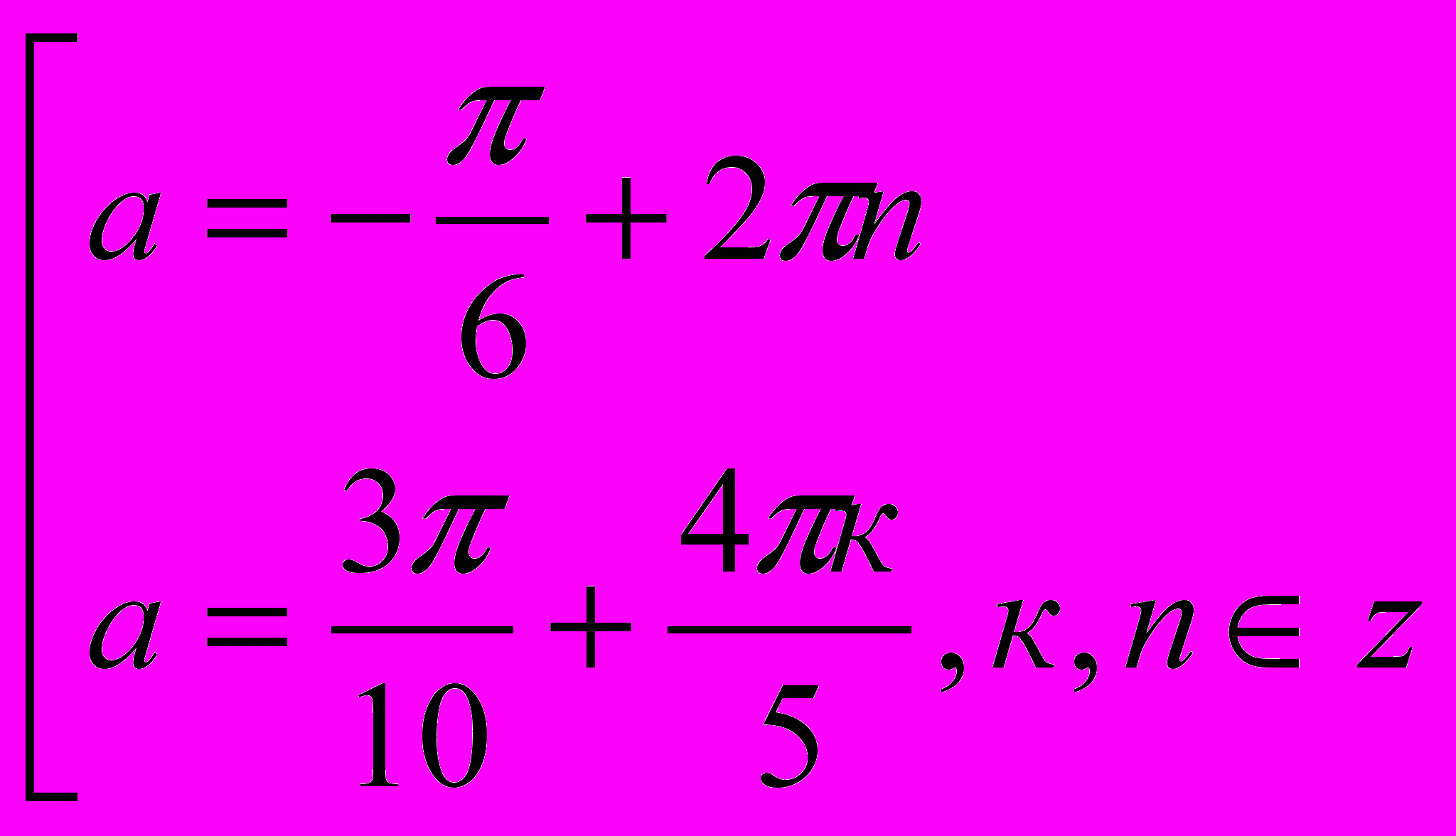
Условие 0
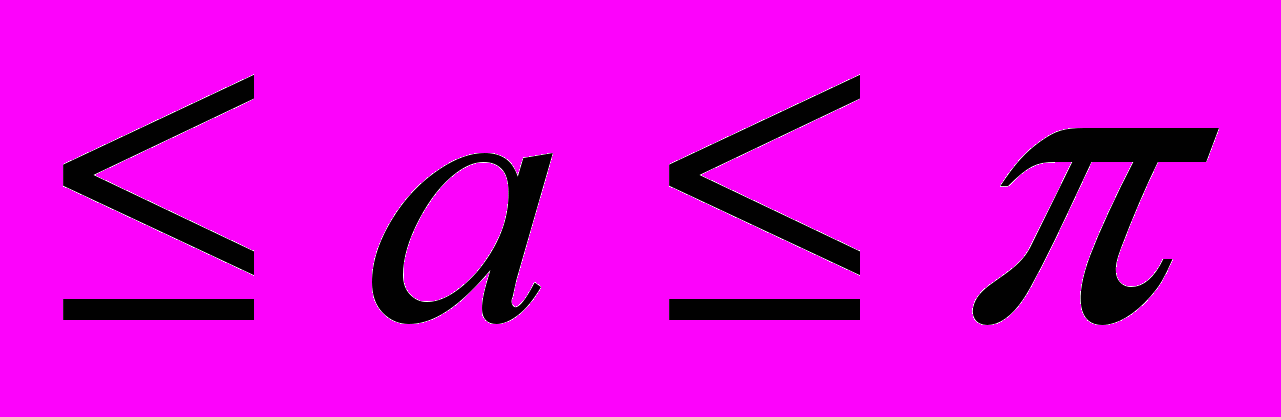 выполняется только при к=0. При этом а=
выполняется только при к=0. При этом а=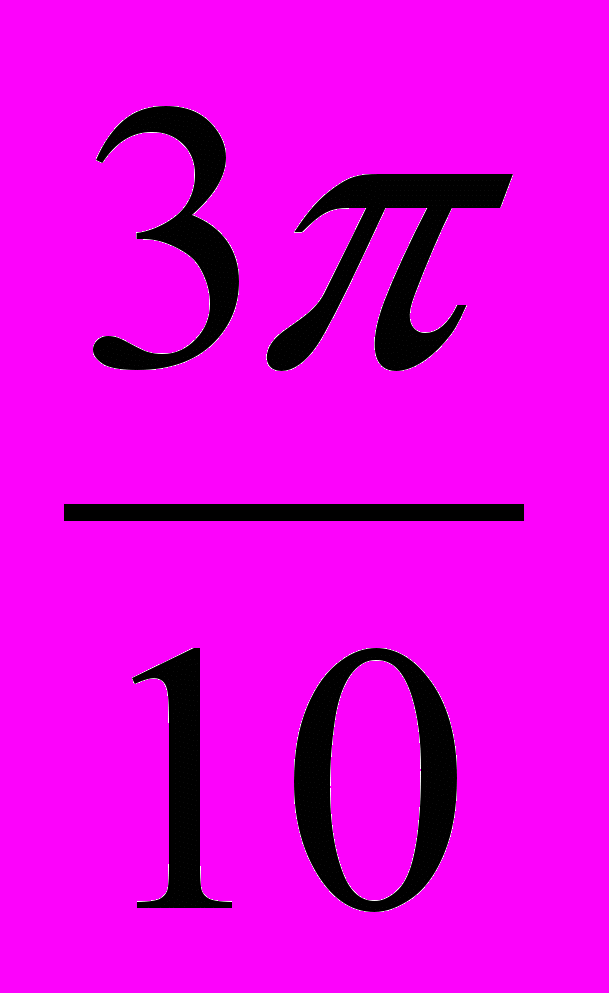 и соответственно х=соs
и соответственно х=соs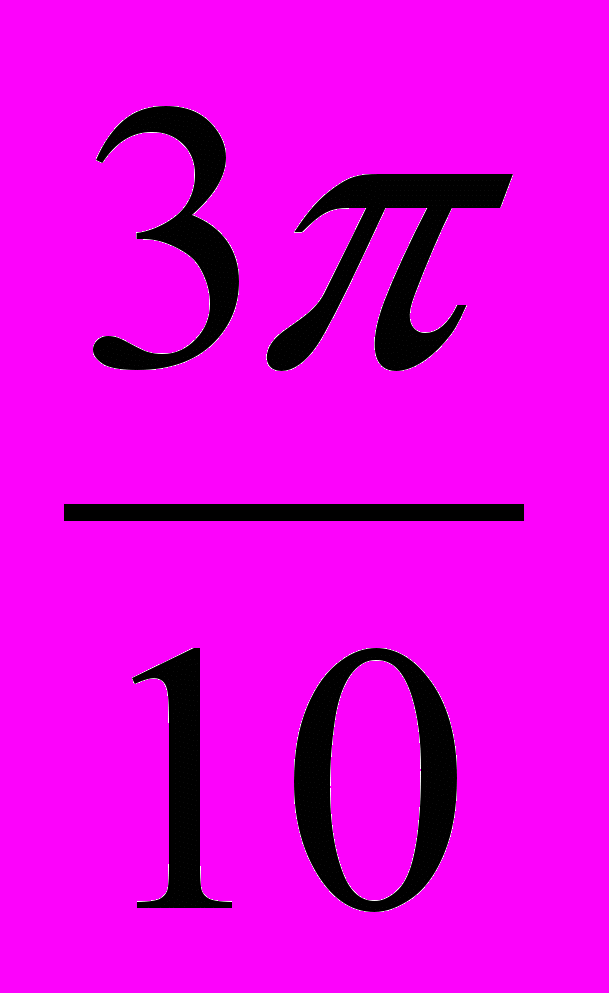
Ответ: х=соs
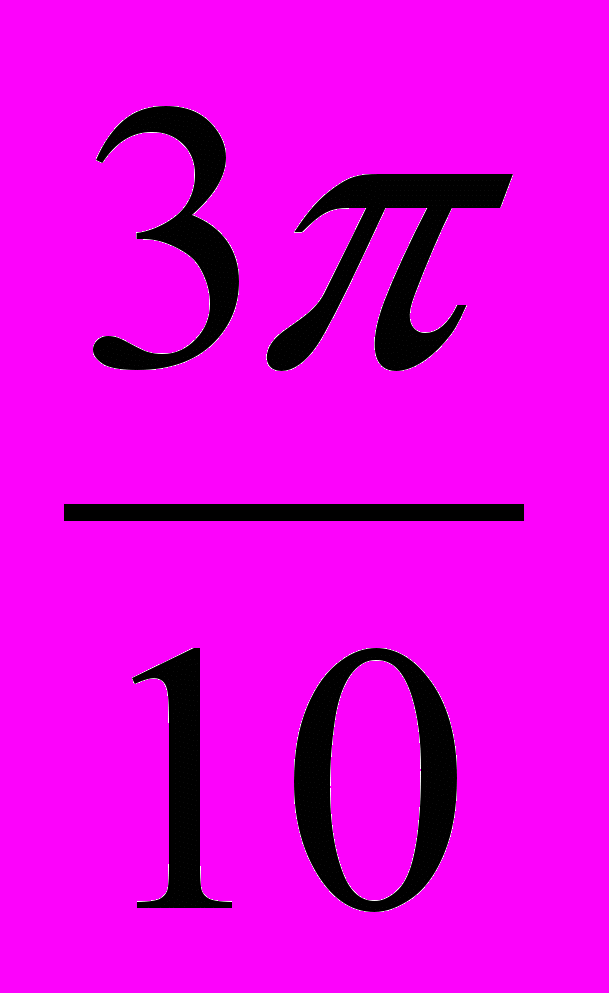
4) Неравенство Коши
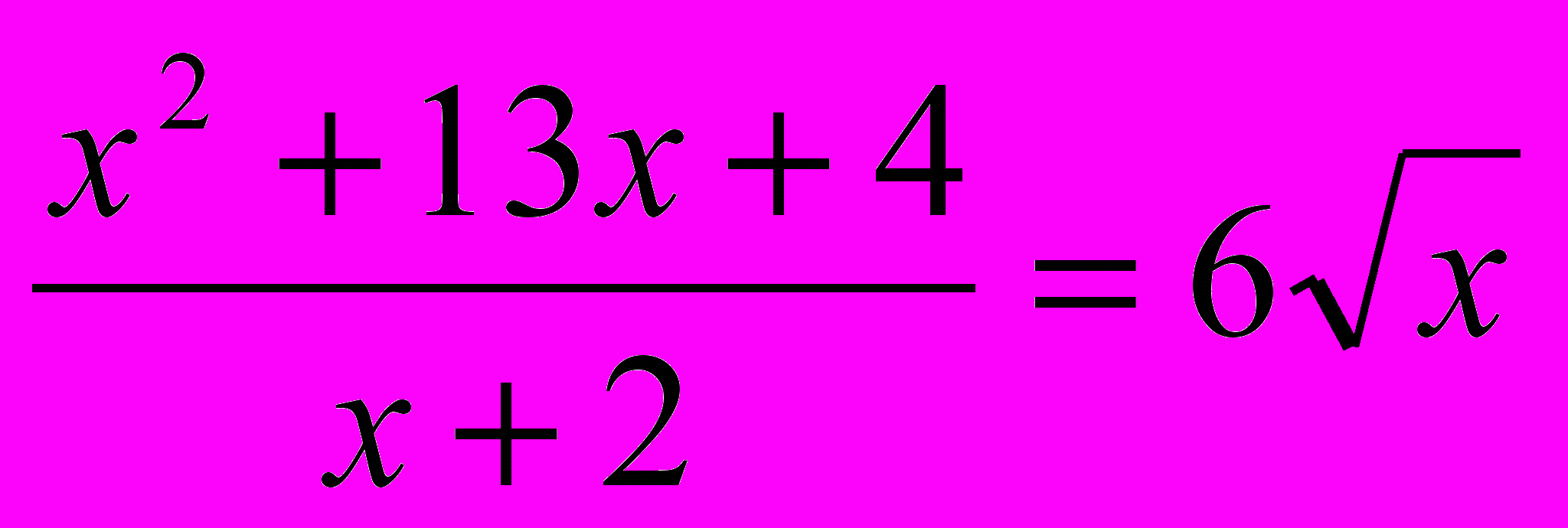
ОДЗ: х
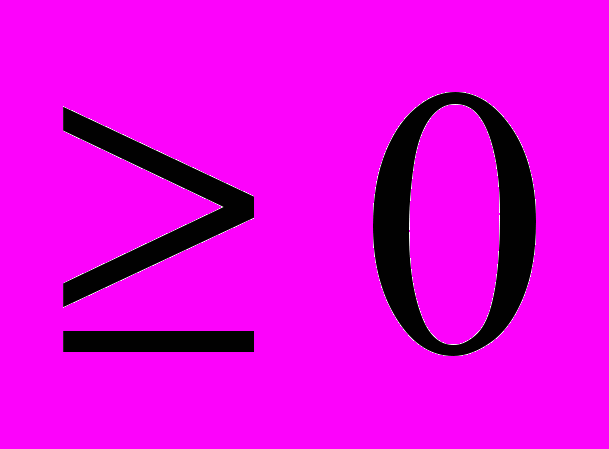
Х+11-

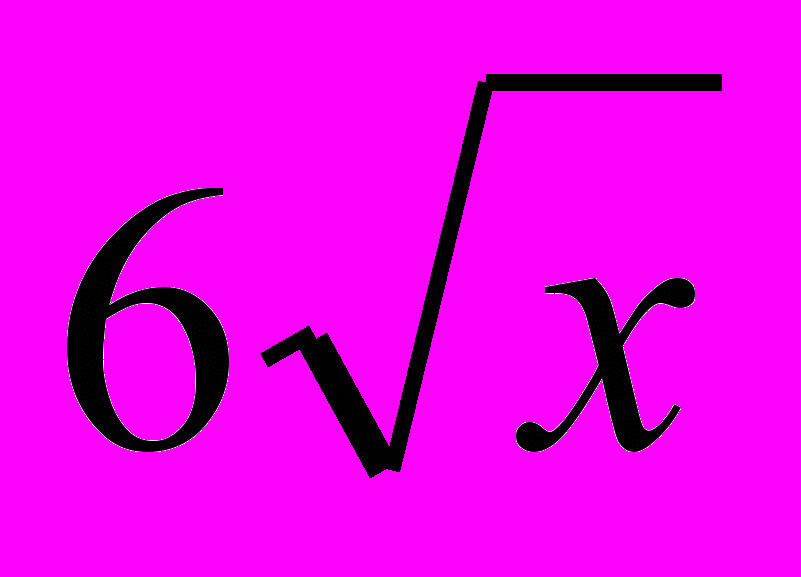
(Х+2)+9-

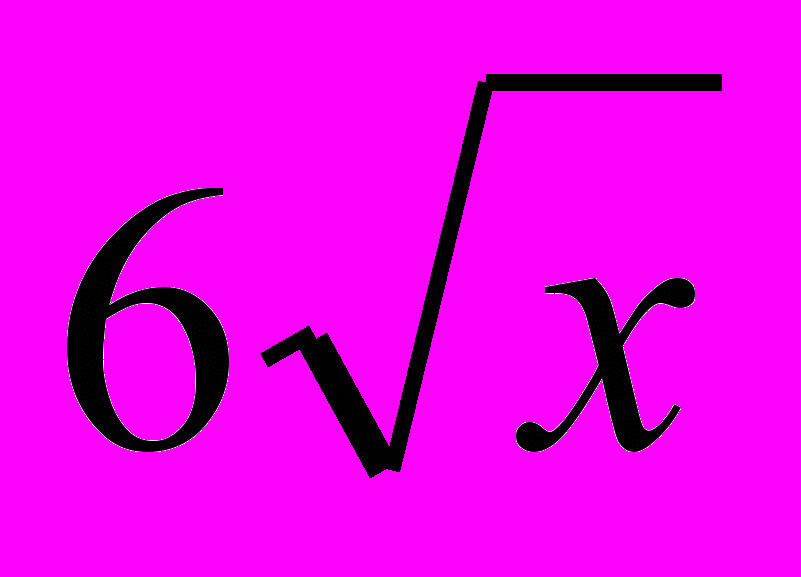 Х+2+
Х+2+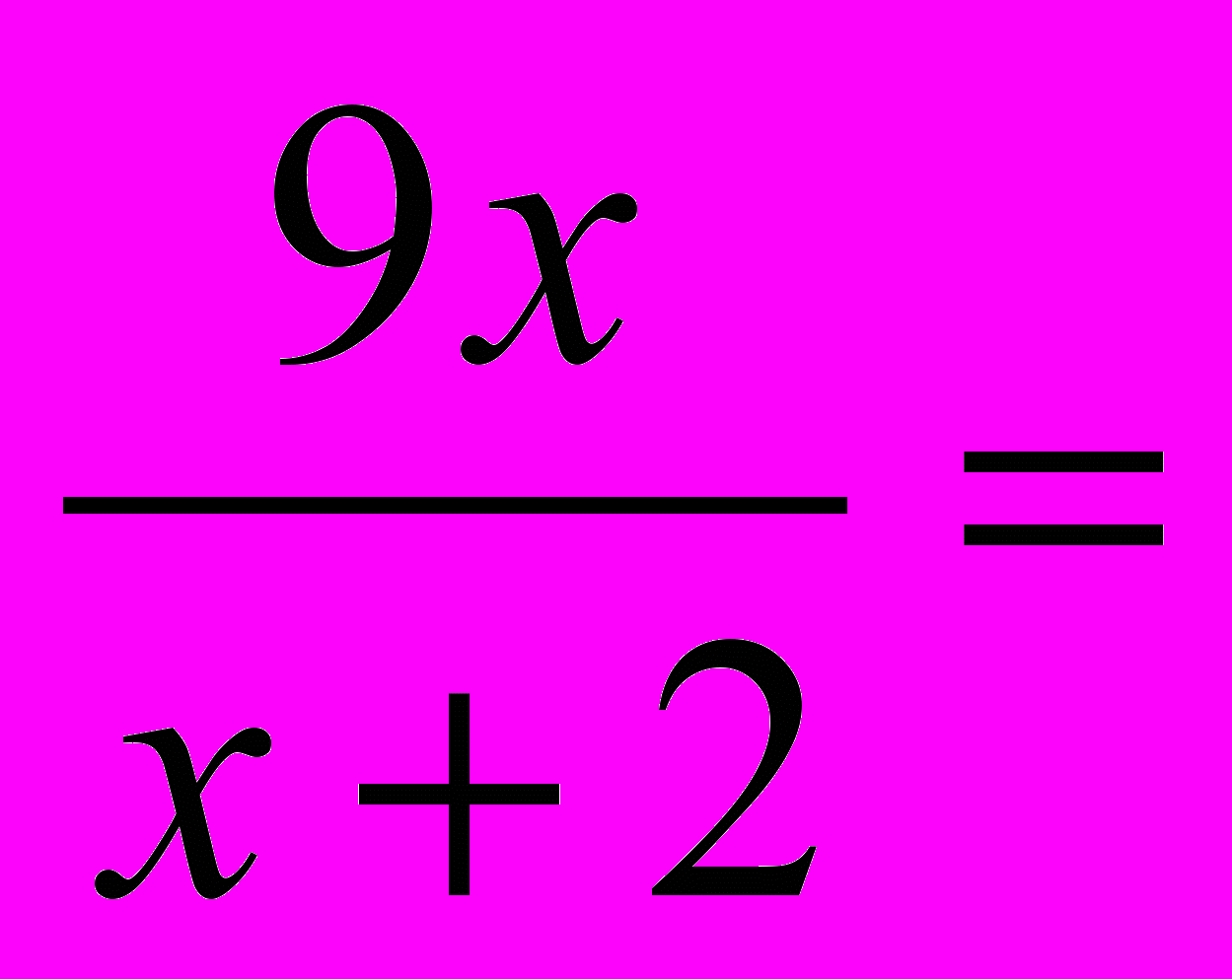
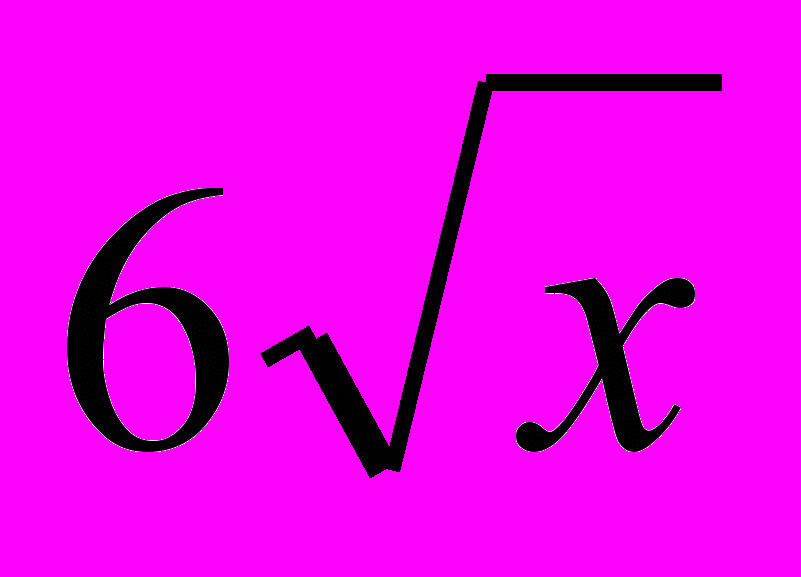
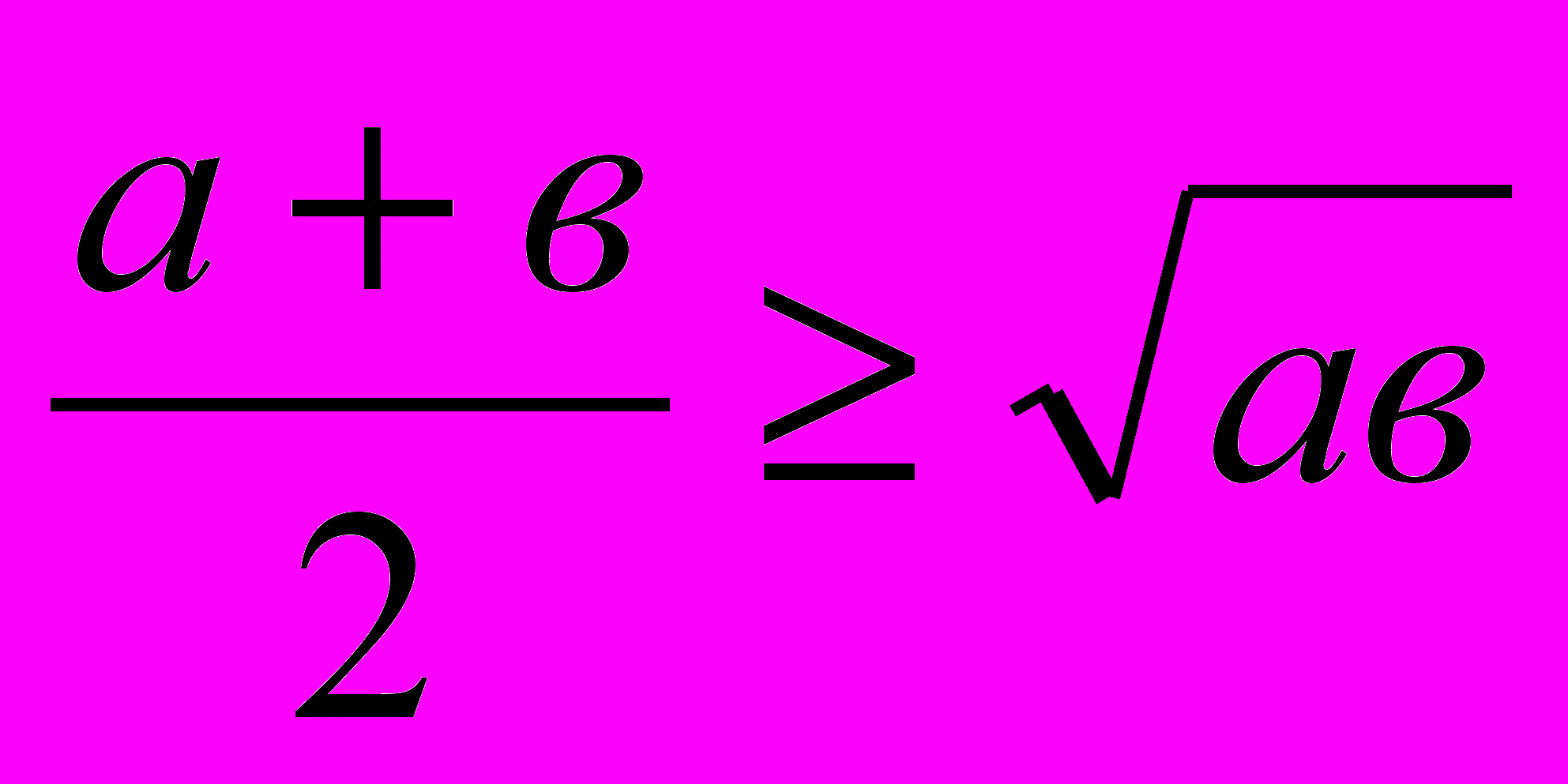 , если а
, если а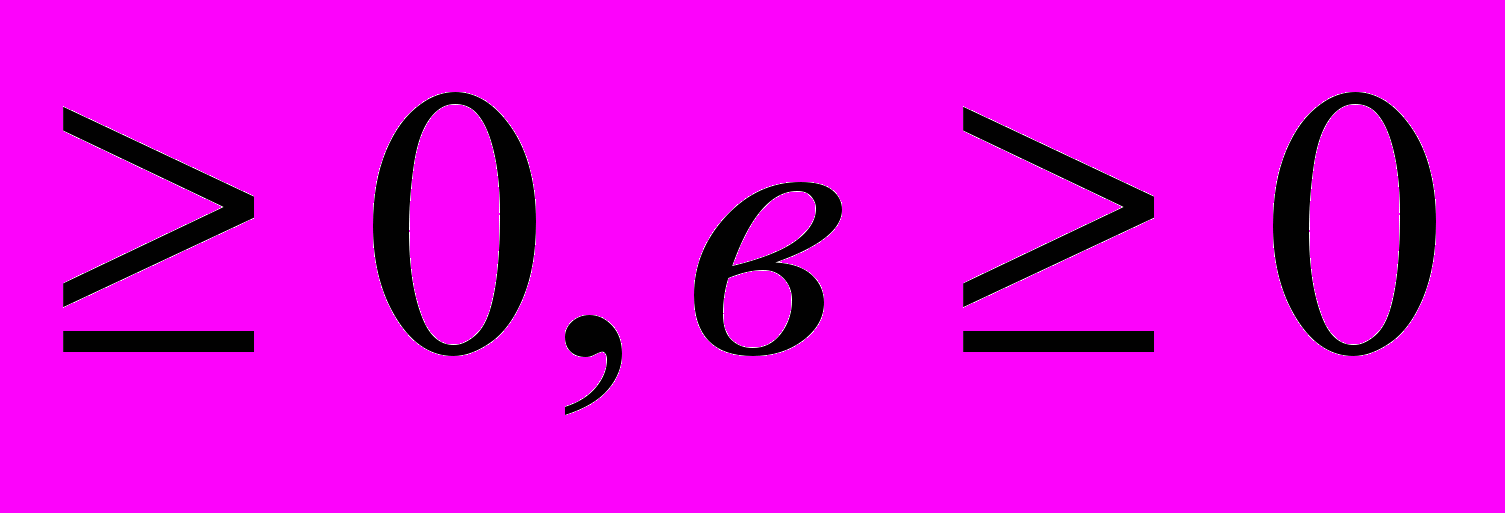
а+в
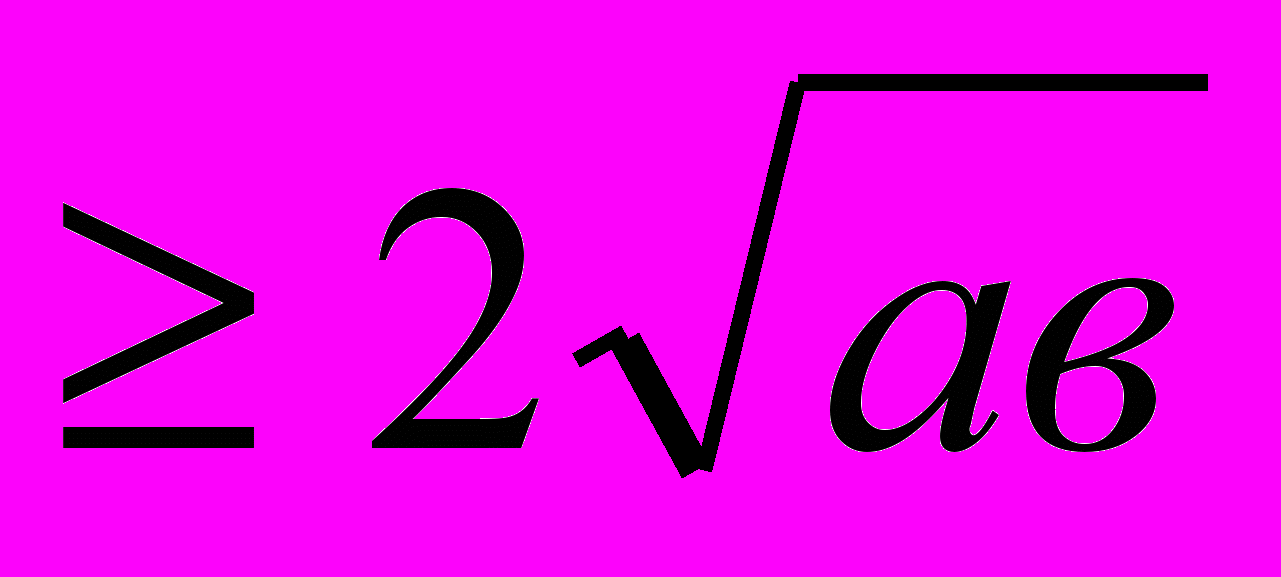
Х+2+
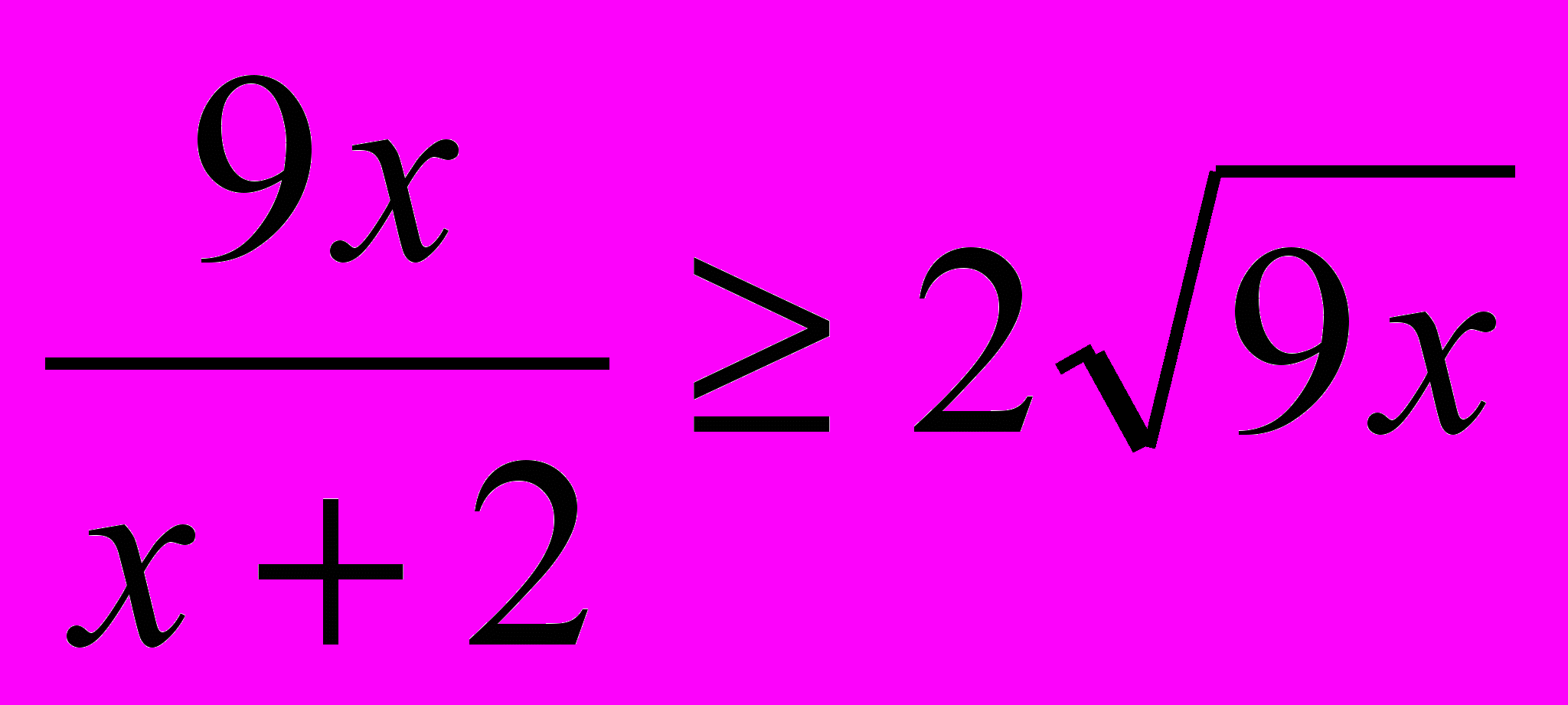 Х+2+
Х+2+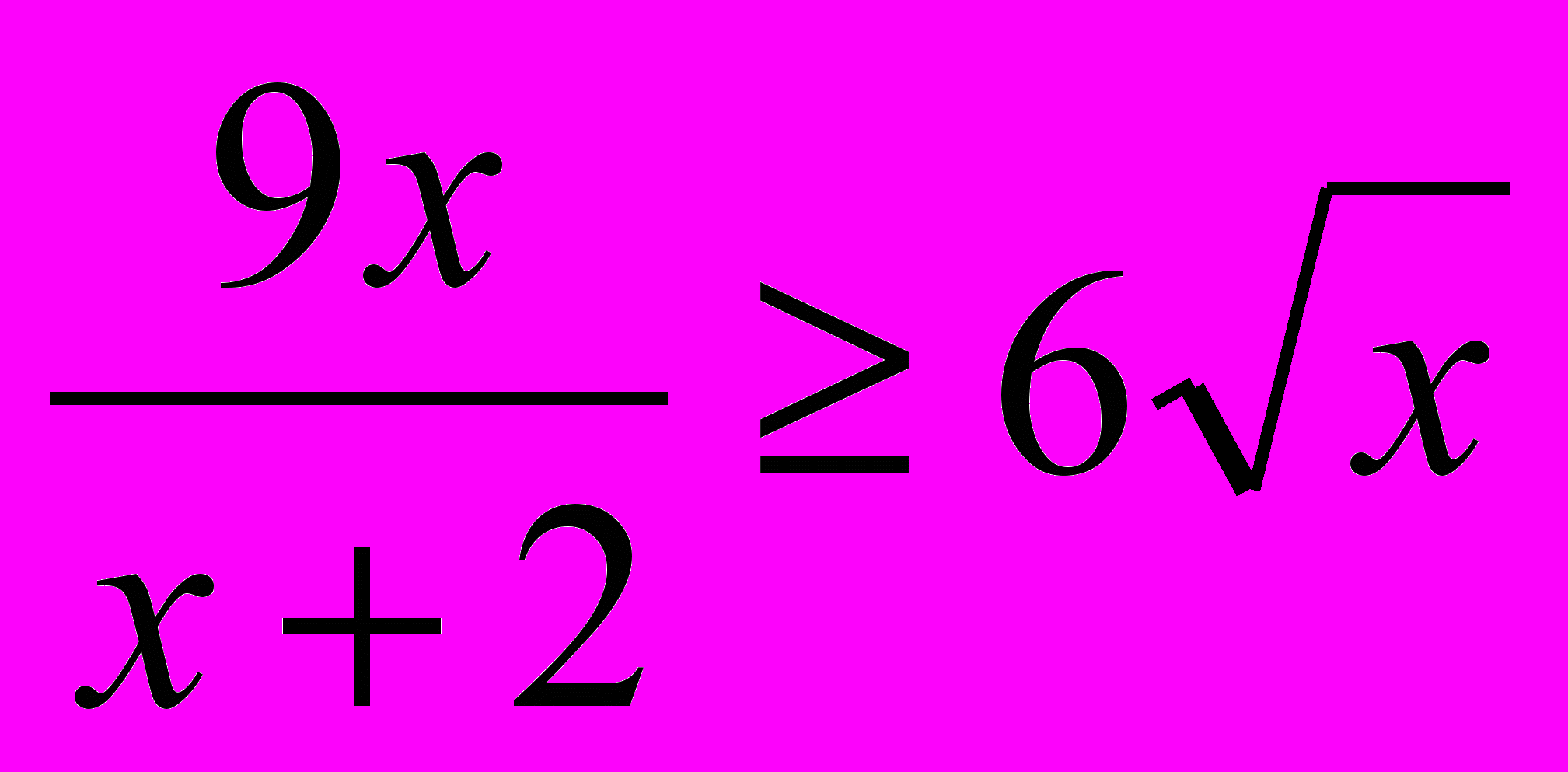
Равенство достигается, если а = в
Х+2=
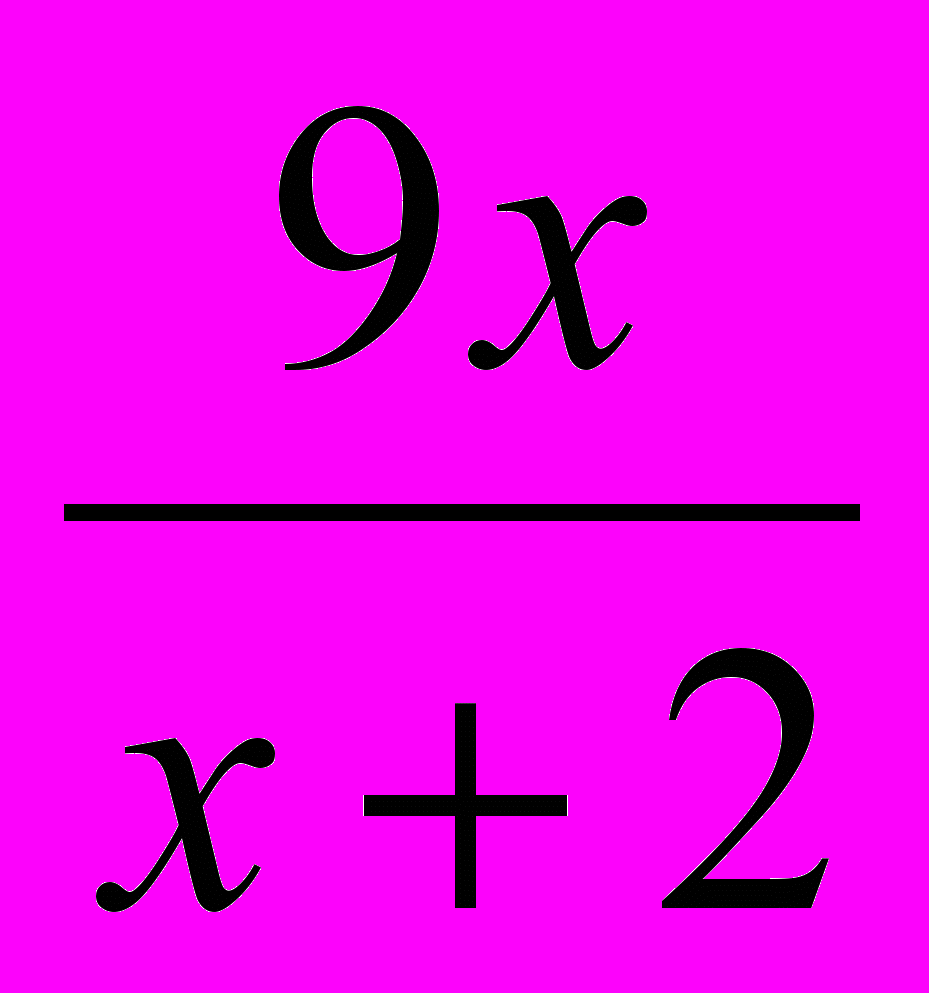
Х2+4х+4=9х
Х2-5х+4=0
Х=4,х=1
Ответ: Х=4,х=1
5) Неравенство треугольника

Введём два вектора так, чтобы левая часть неравенства представляла собой сумму их длин (модулей):
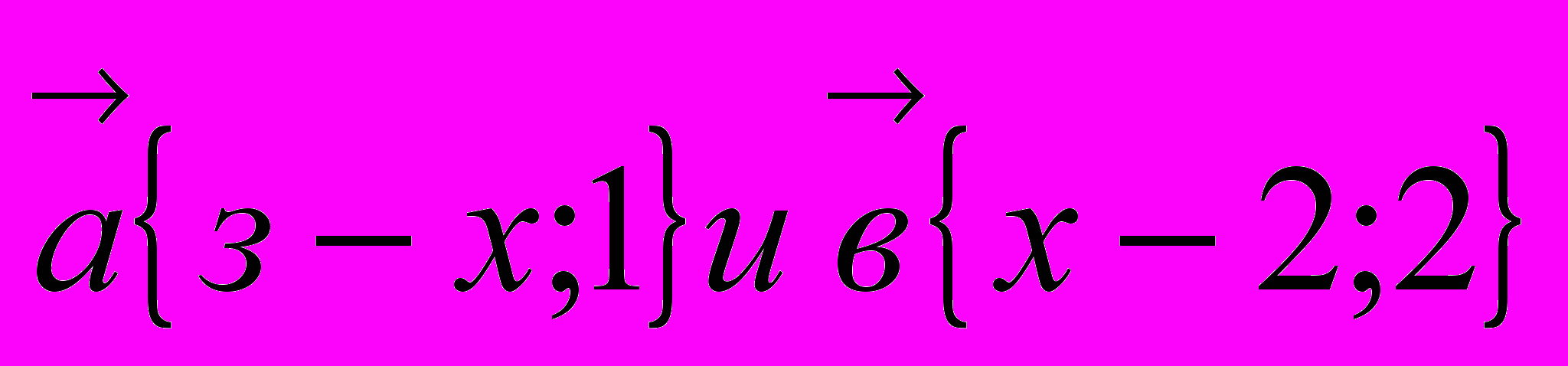 Тогда (
Тогда (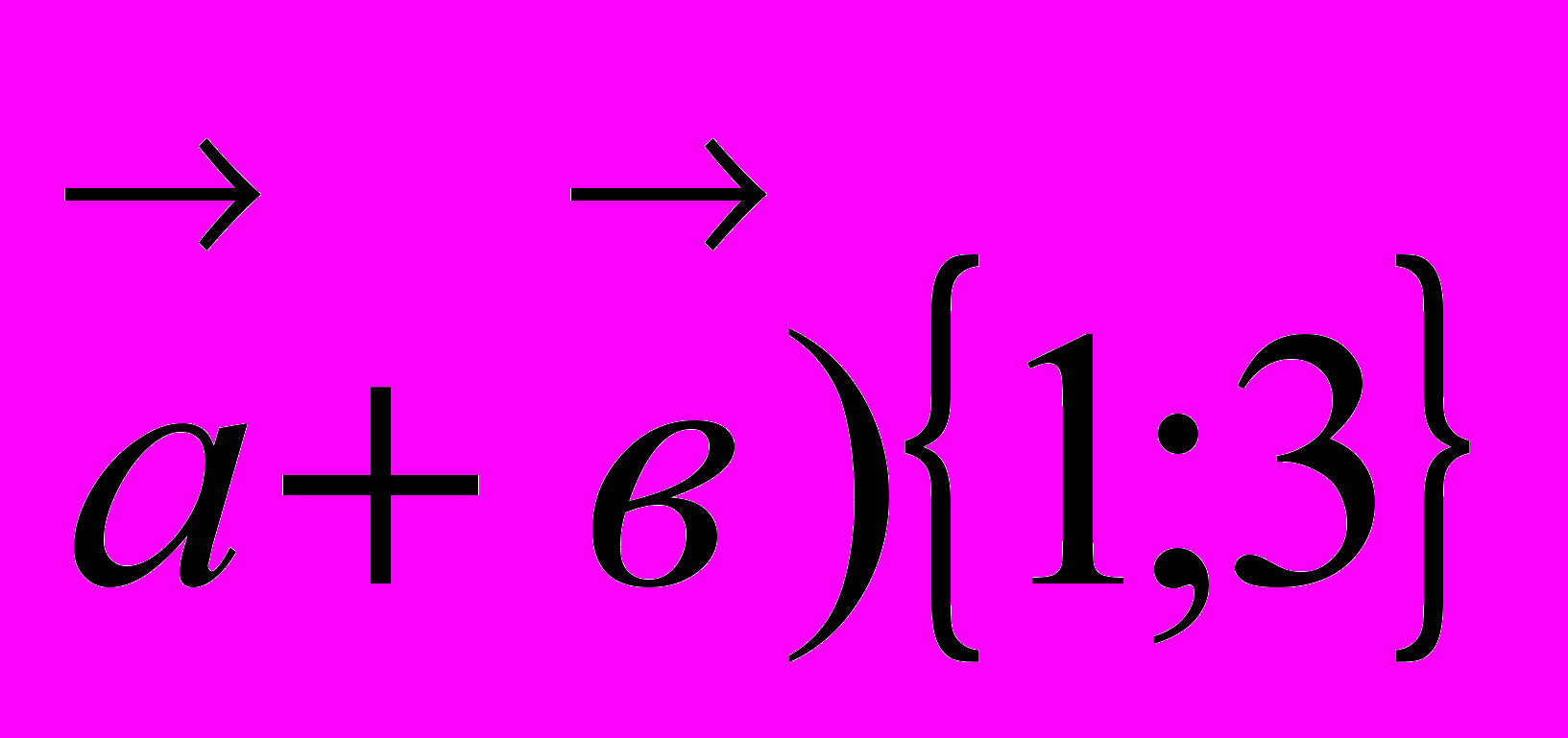 . Следовательно,
. Следовательно,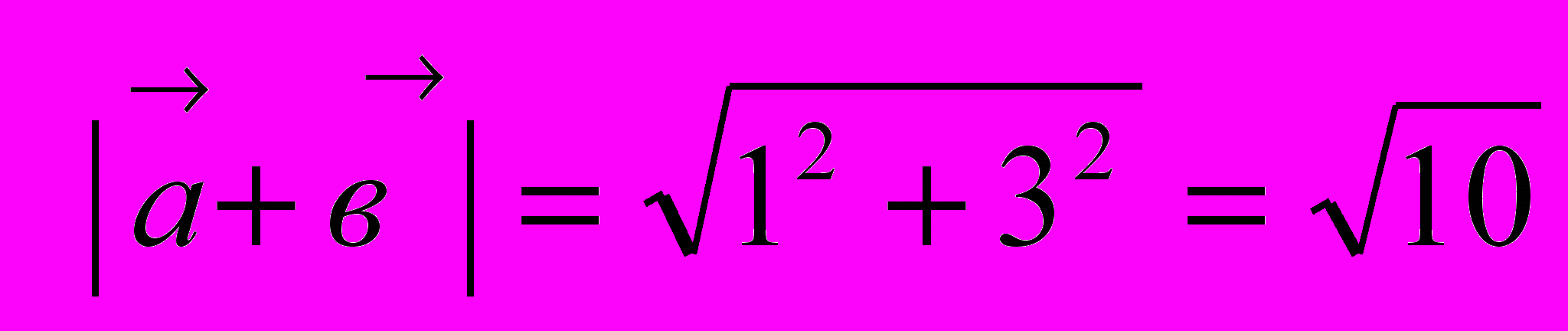
Таким образом, данное неравенство имеет вид:
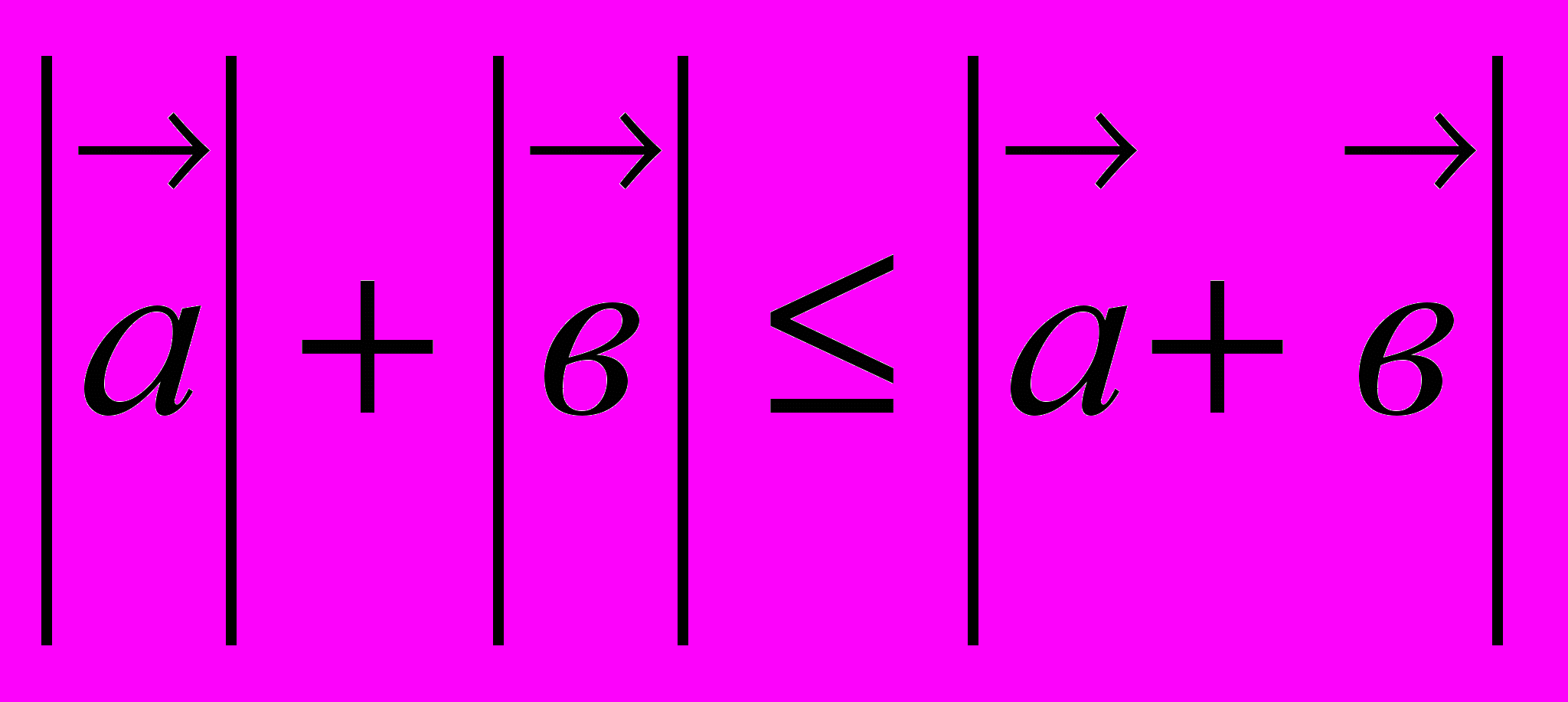
Поскольку для любых двух векторов
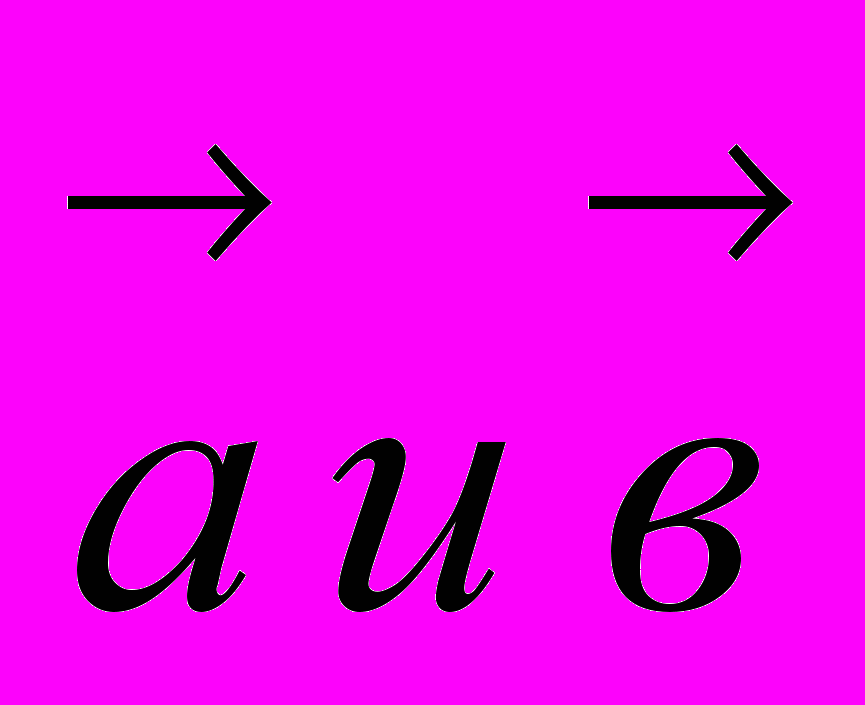 справедливо неравенство:
справедливо неравенство:  , то получим
, то получим 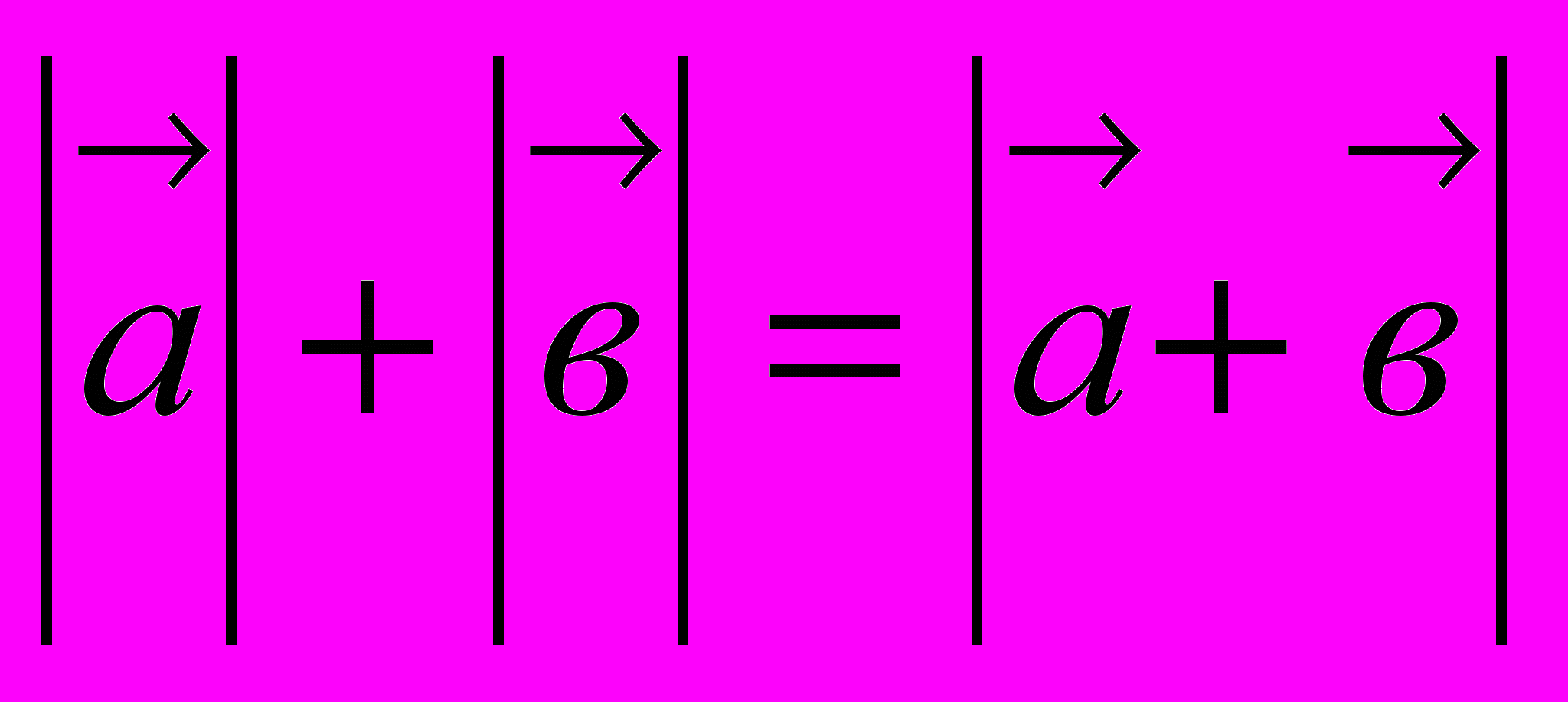 Это возможно в том и только том случае, если векторы сонаправлены. Два ненулевых вектора сонаправлены, если отношения их соответственных координат равны одному и тому же положительному числу. В данном случае условие сонаправленности имеет вид
Это возможно в том и только том случае, если векторы сонаправлены. Два ненулевых вектора сонаправлены, если отношения их соответственных координат равны одному и тому же положительному числу. В данном случае условие сонаправленности имеет вид 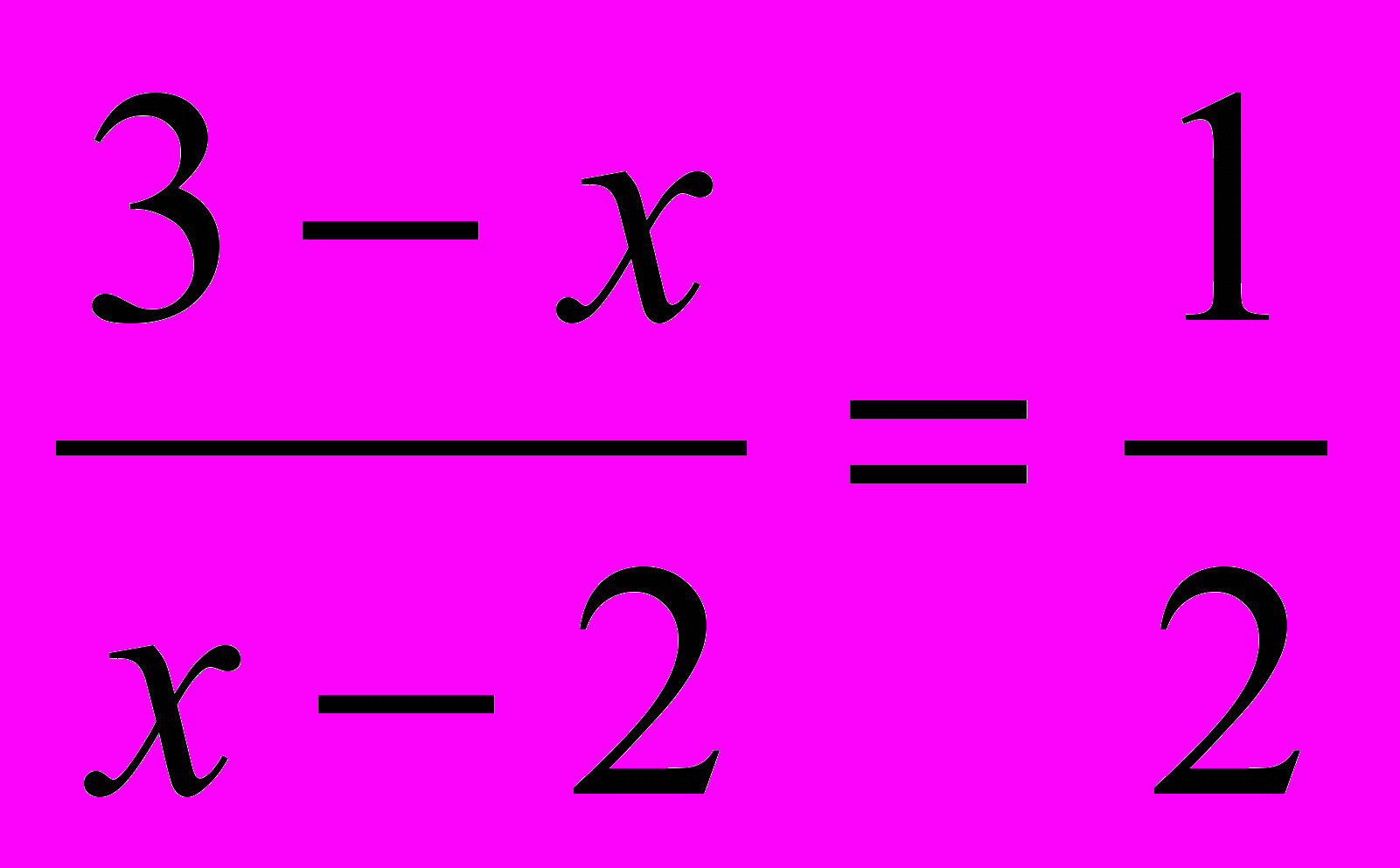 , откуда х =
, откуда х =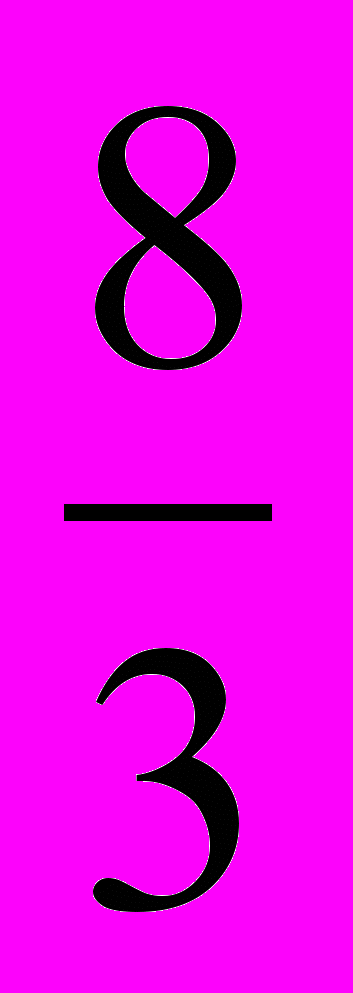 Ответ: х =
Ответ: х =
Далее учащиеся выполняют самостоятельную работу парами по индивидуальным вариантам:
| Вариант 1 | Вариант 2 |
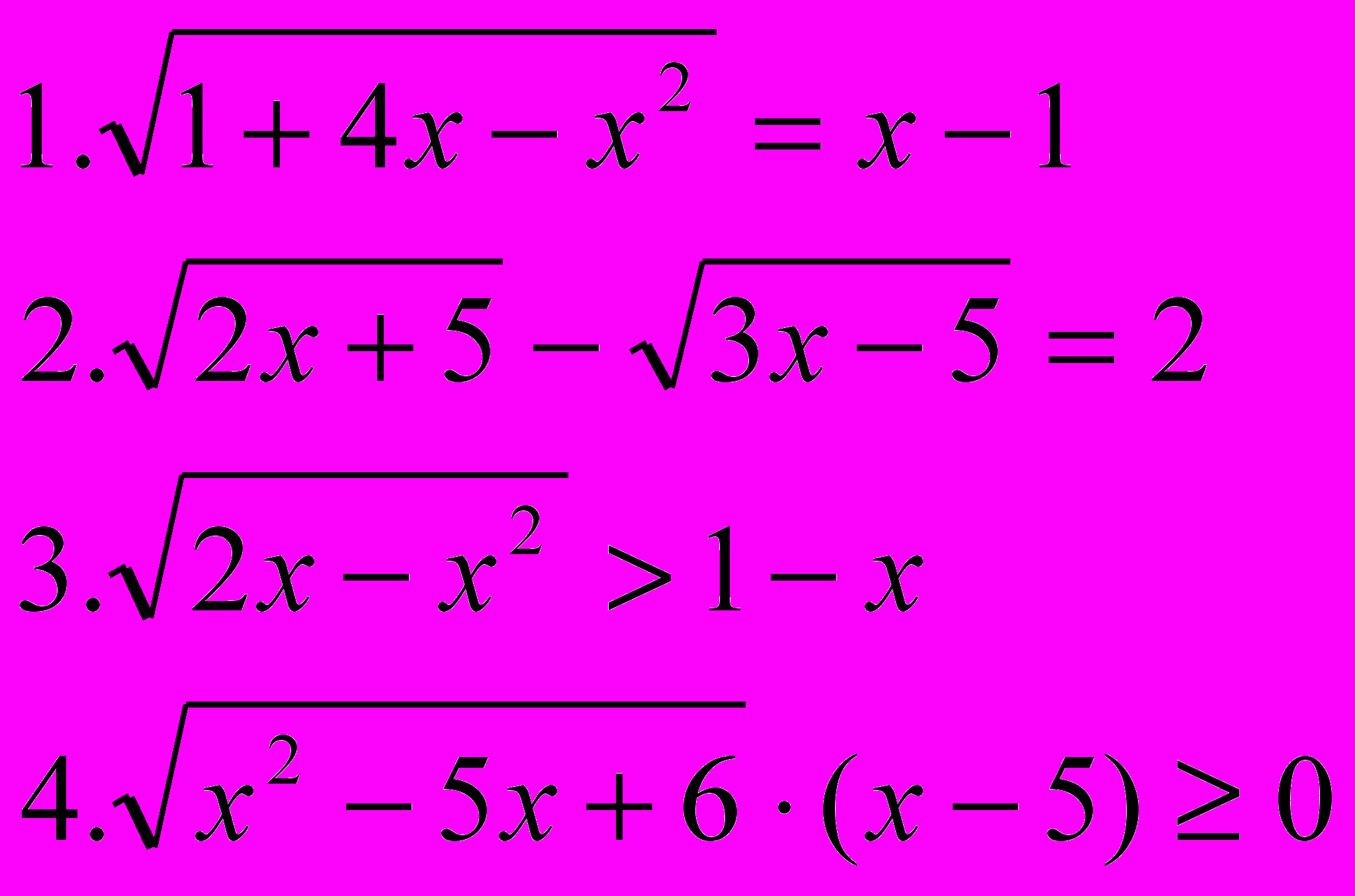 | 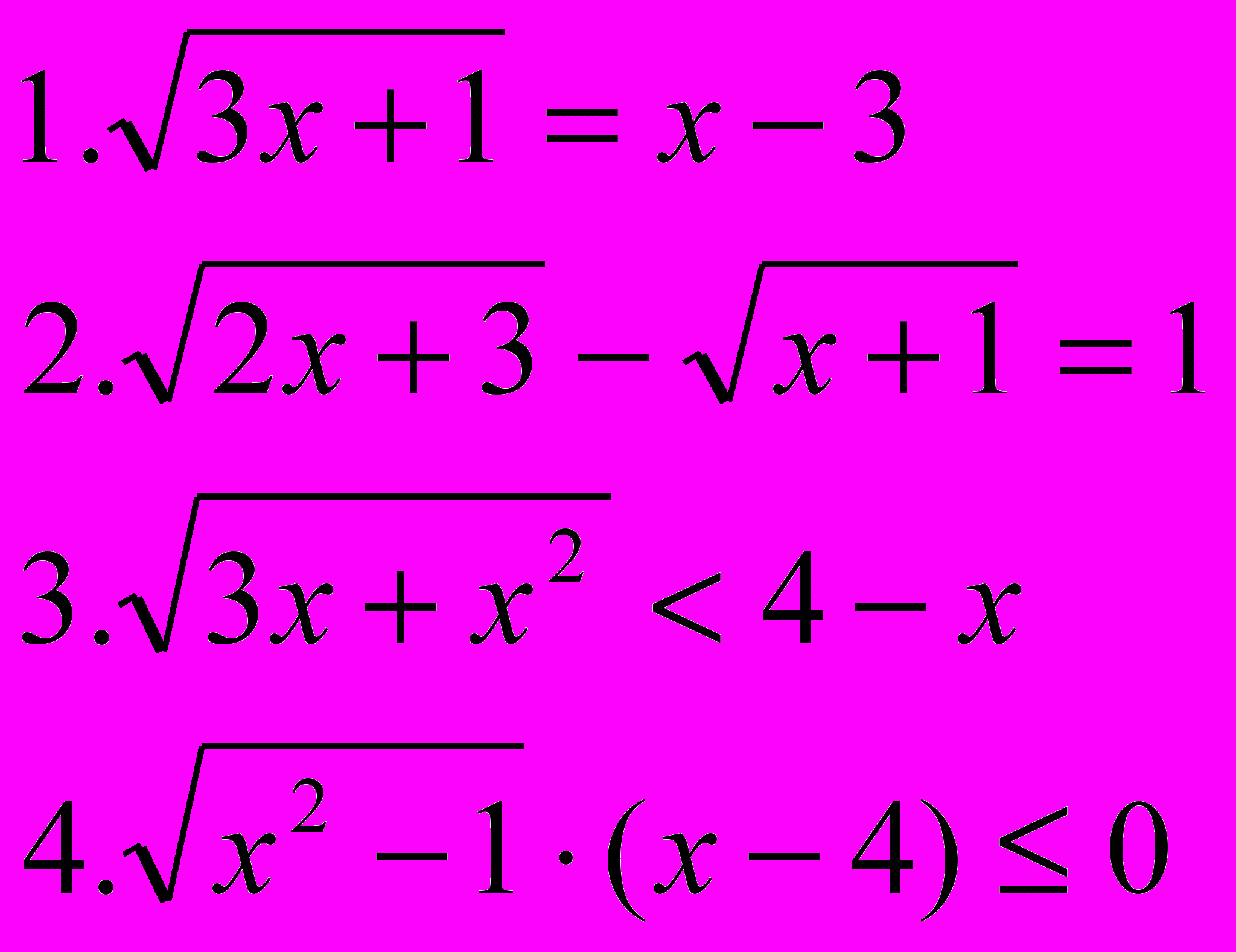 |
| Вариант 3 | Вариант 4 |
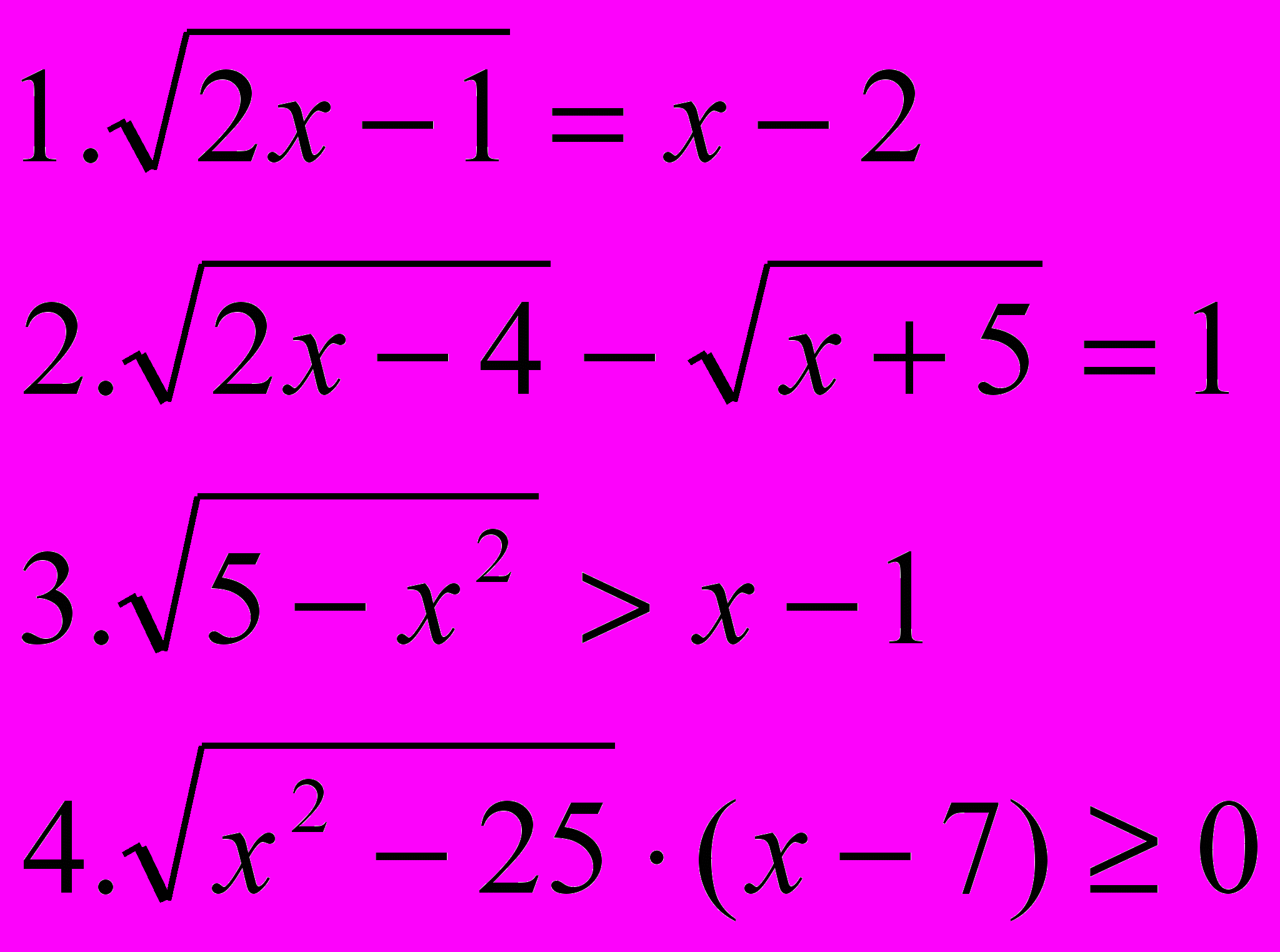 | 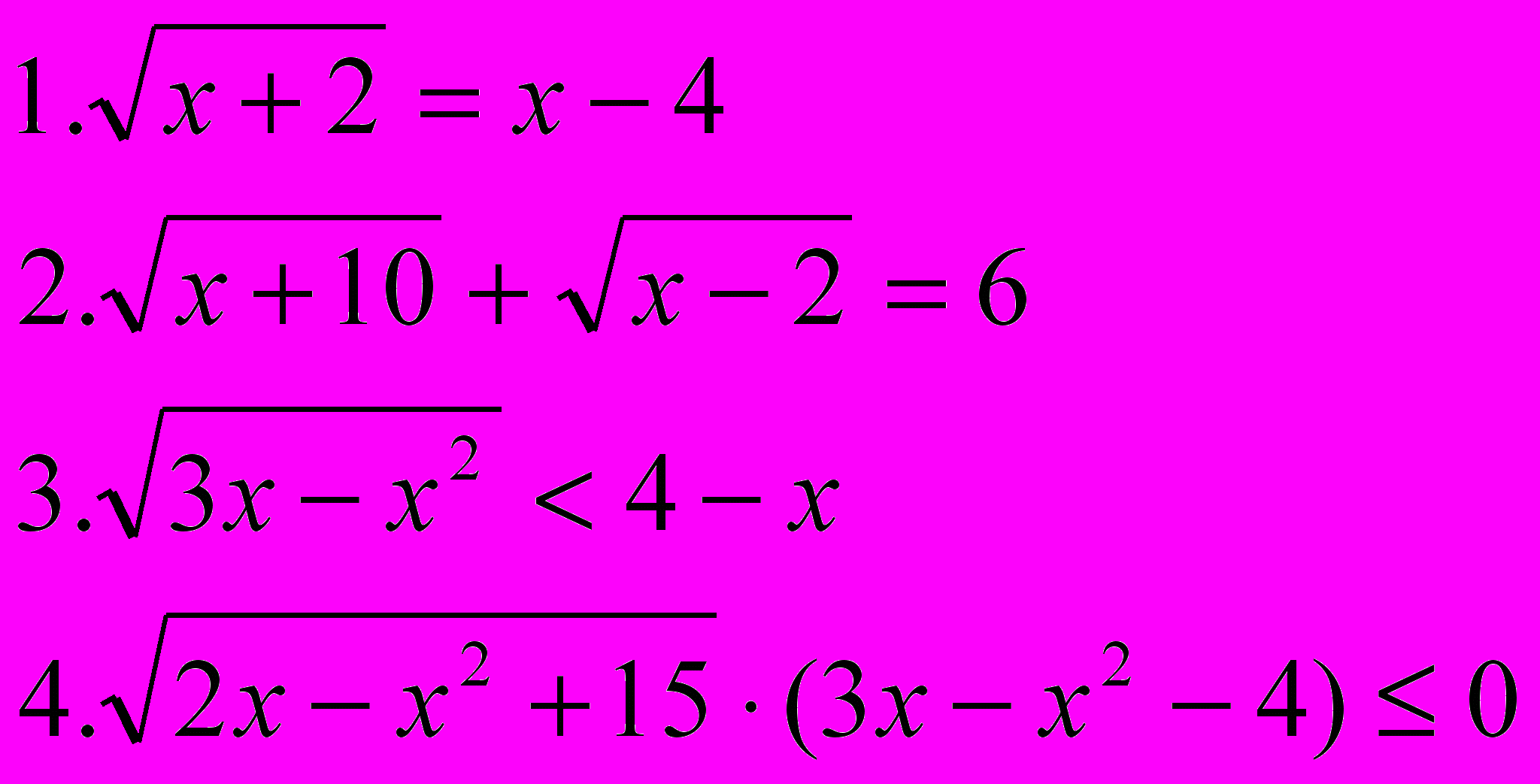 |
| Вариант 5 | Вариант 6 |
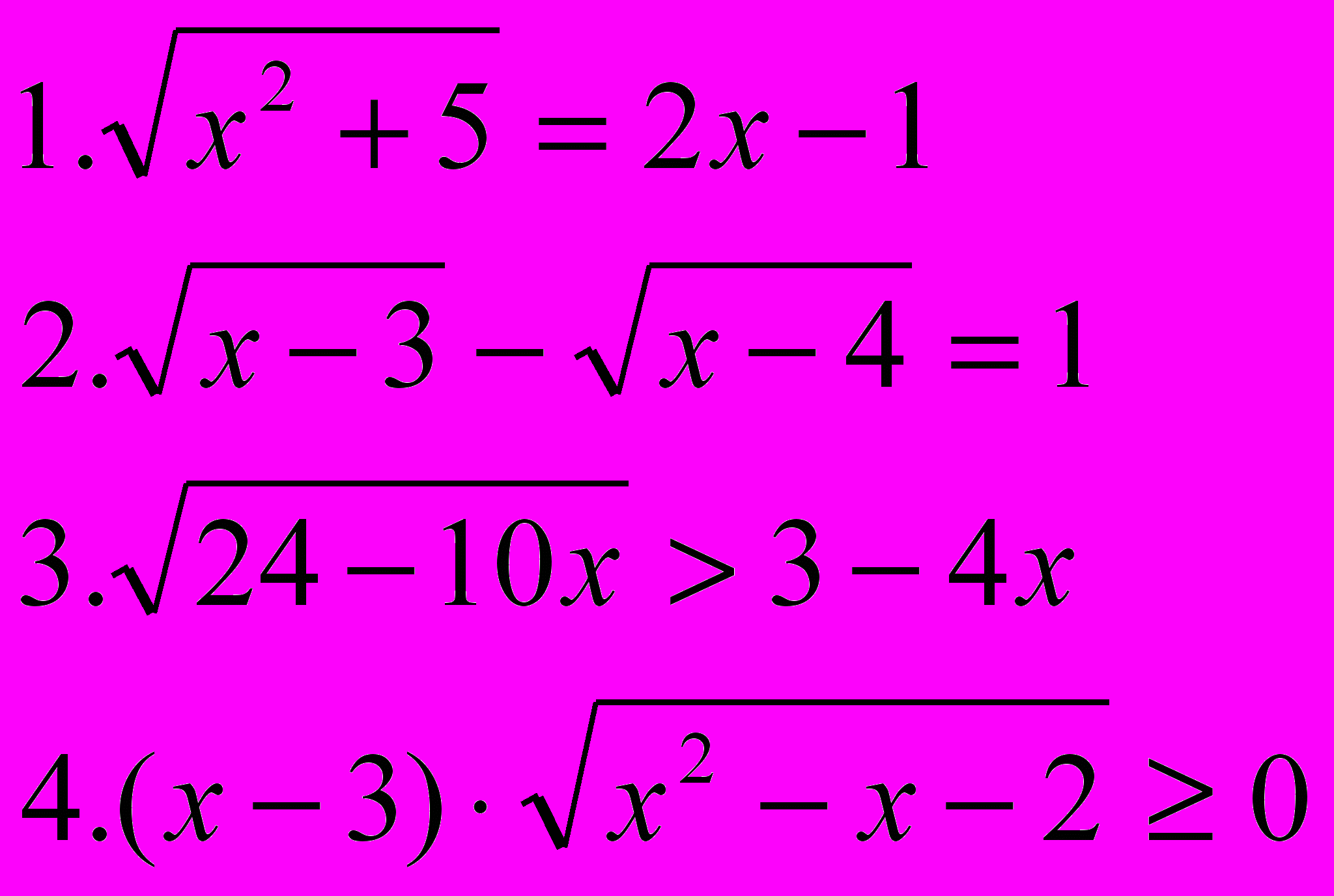 | 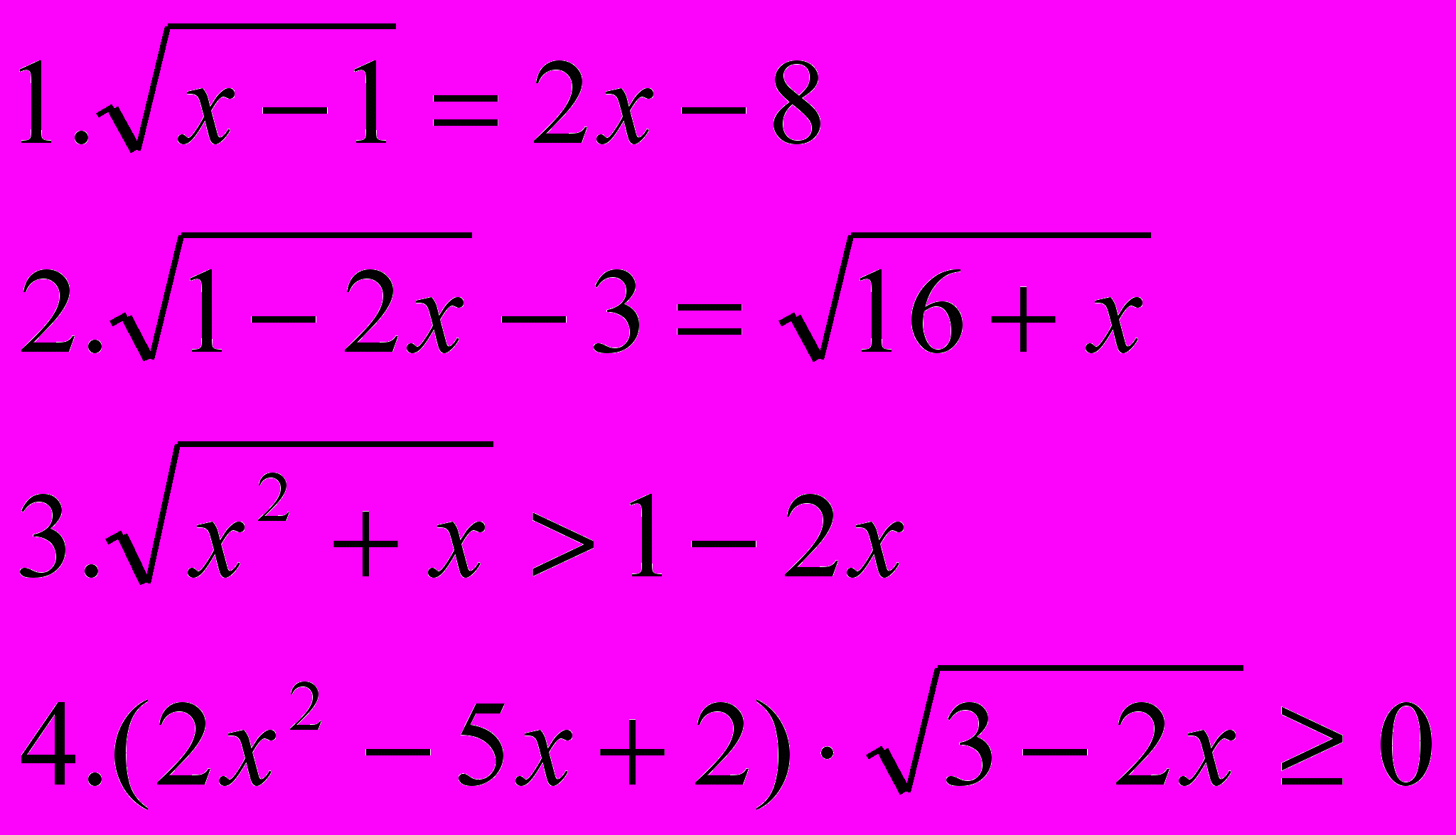 |
| Вариант 7 | Вариант 8 |
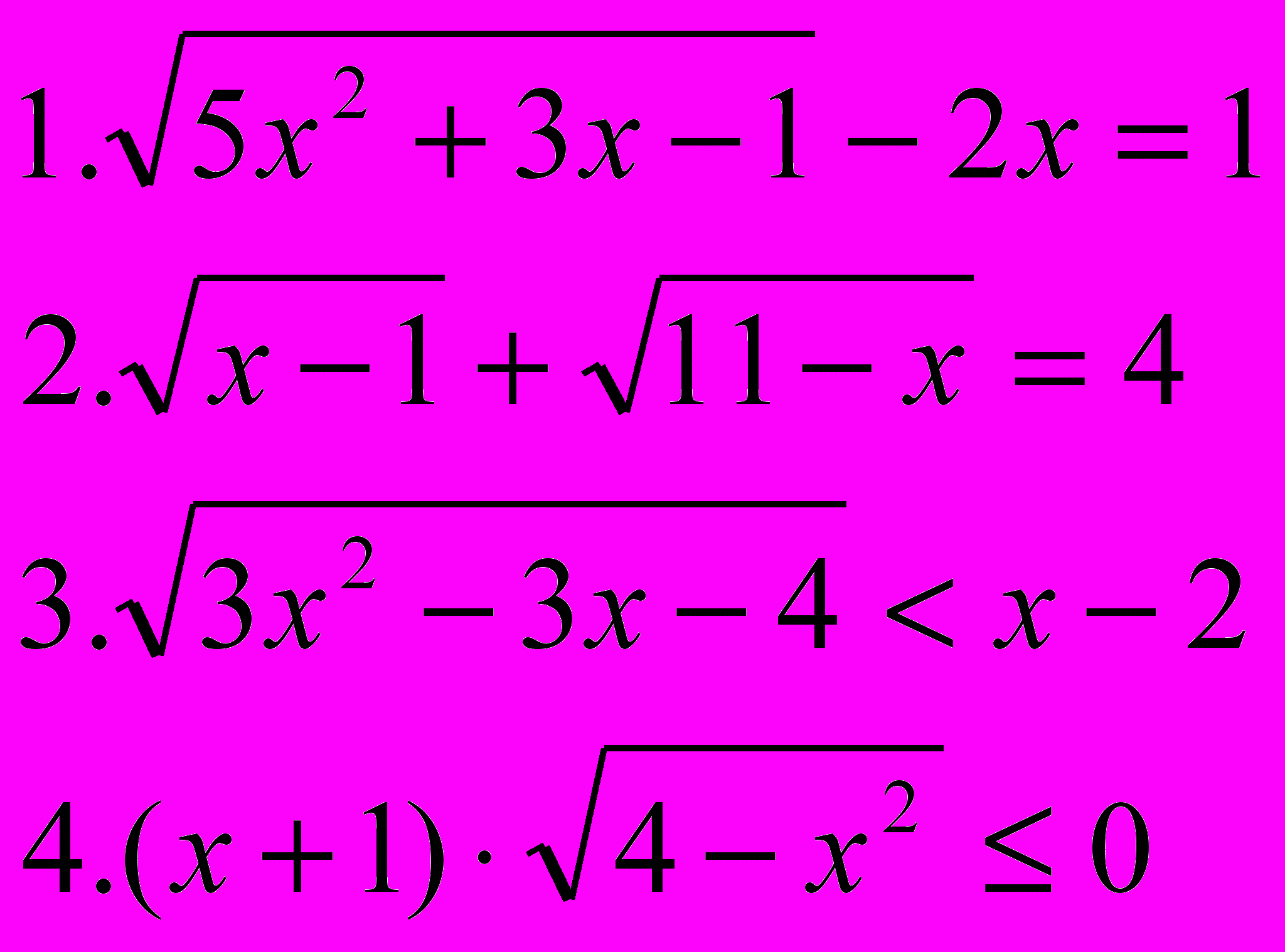 | 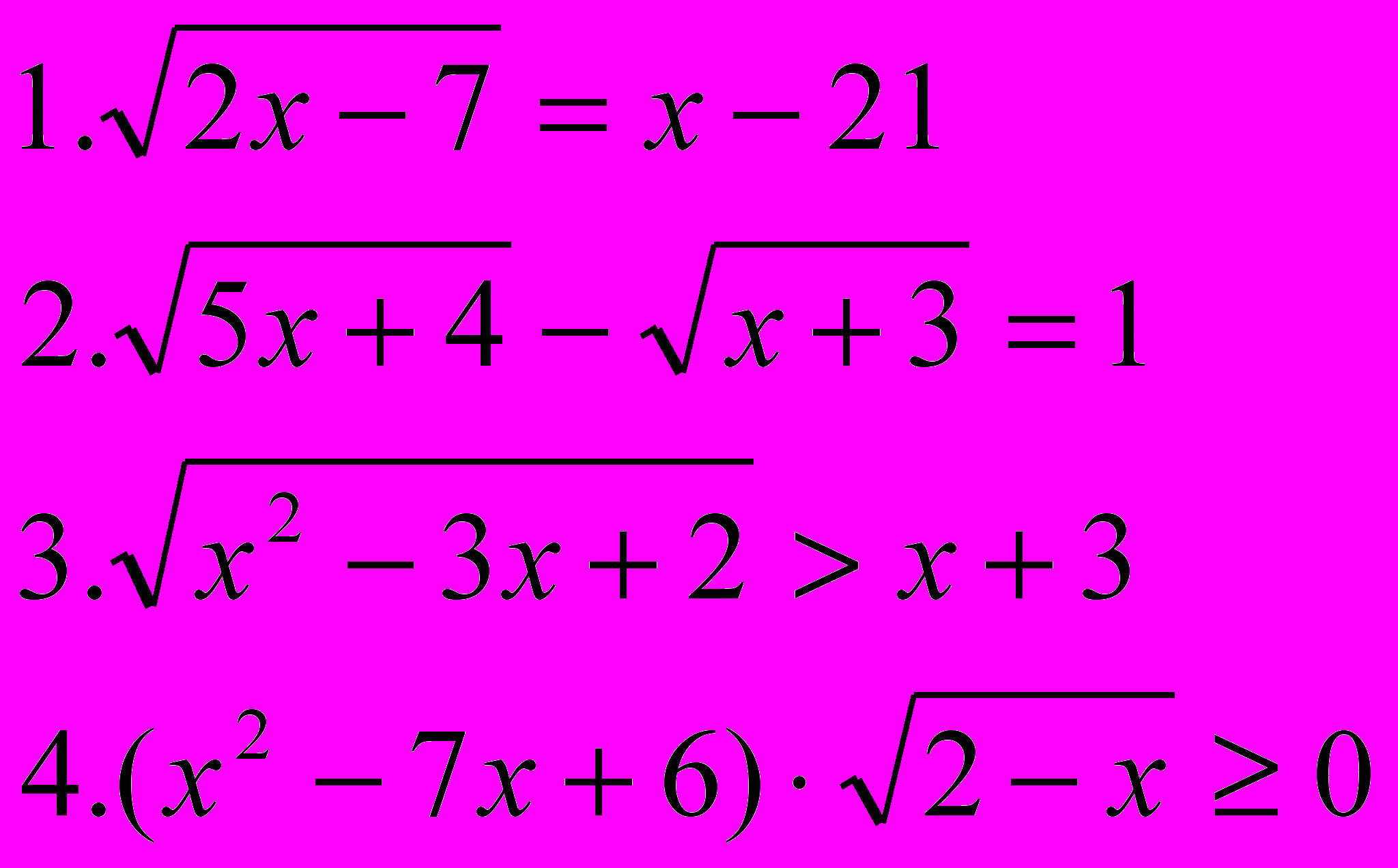 |
| Вариант 9 | Вариант 10 |
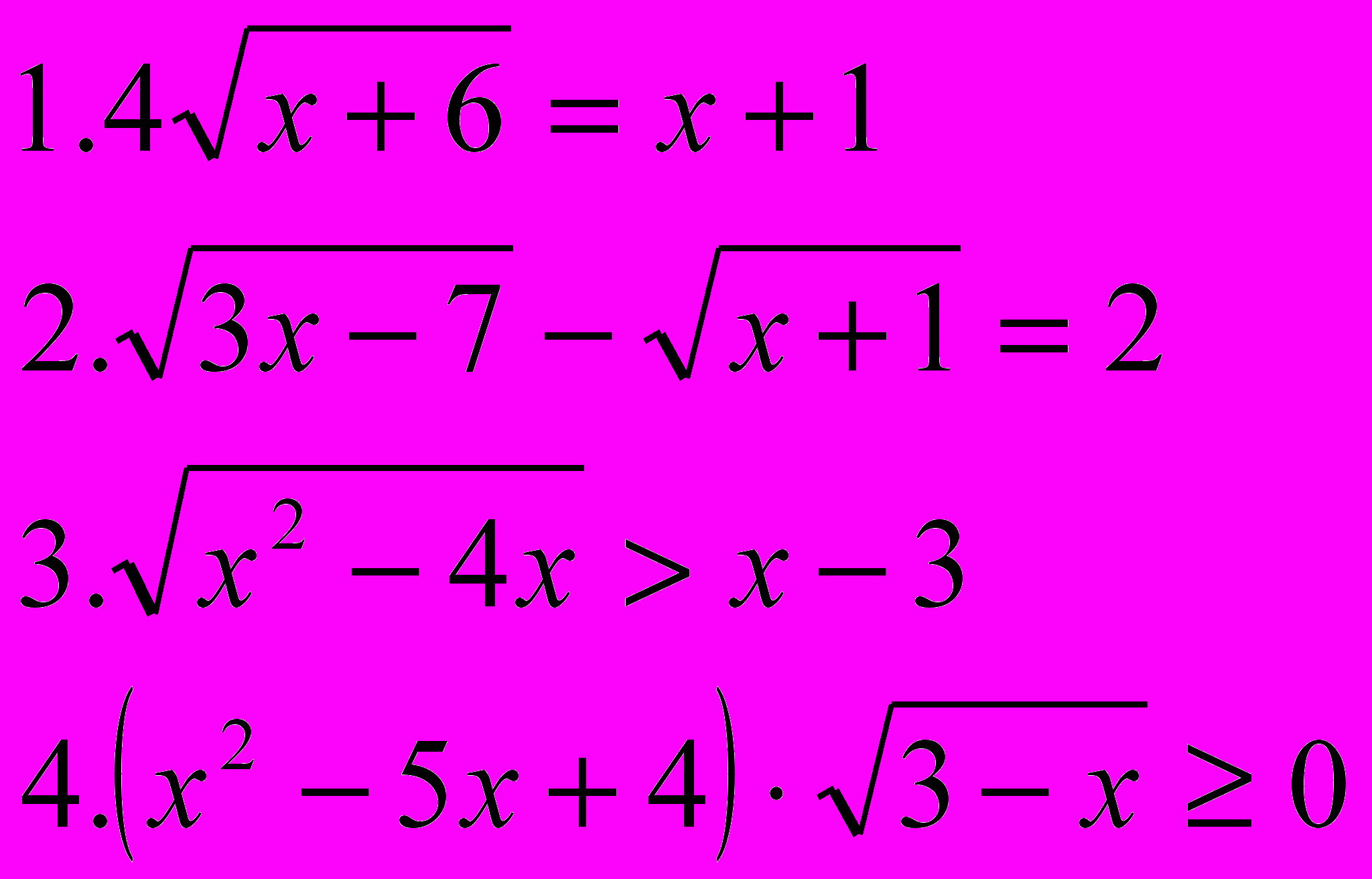 | 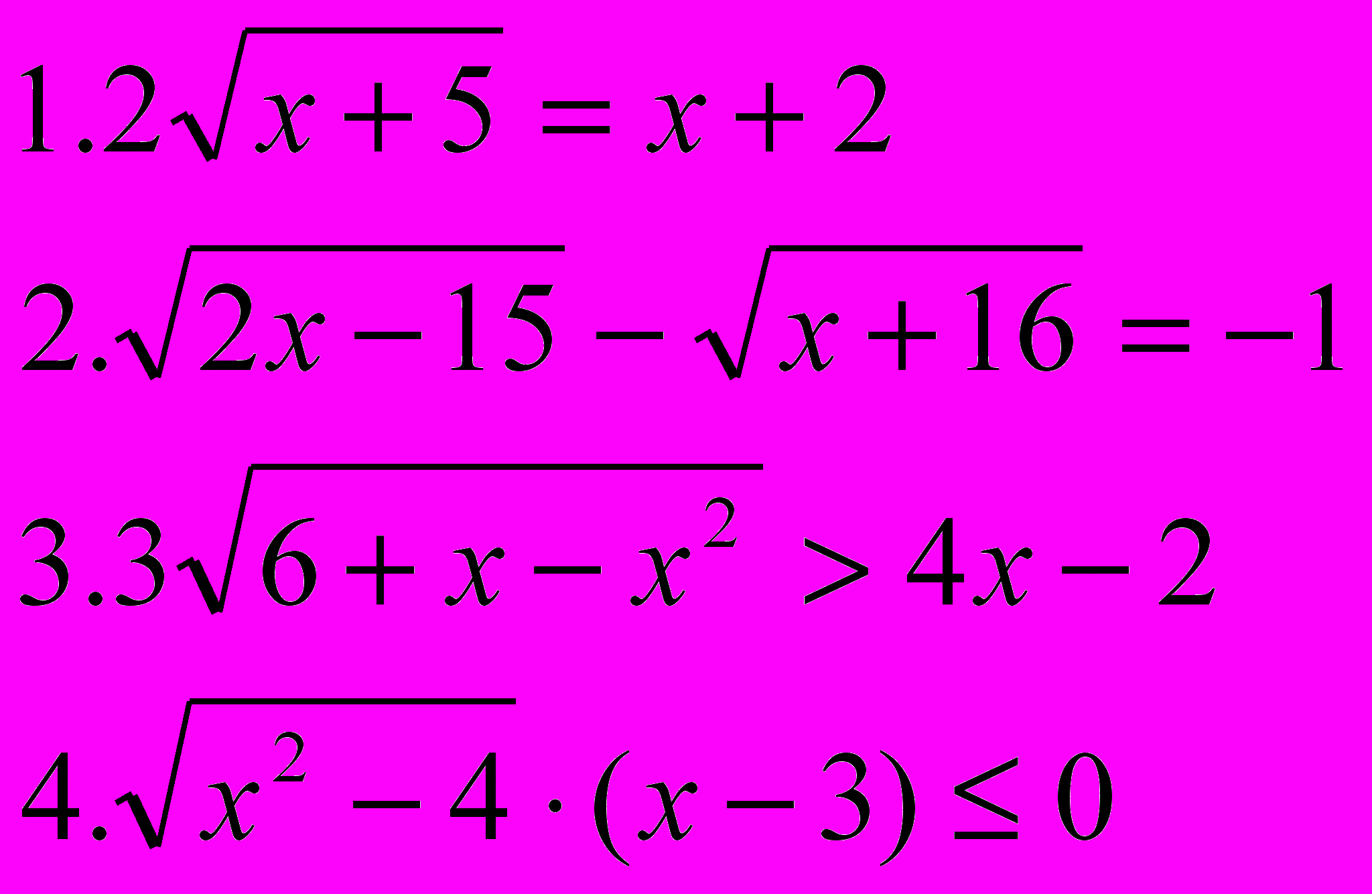 |
Учащиеся решают два задания из 4-х: одно неравенство и одно уравнение, выбирая сами, оценивая уровень сложности. Учащиеся набирают своё решение на компьютере и выводят на печать, работы оцениваются.
Домашнее задание: учащимся даются другие варианты выполняемой работы.
На следующем уроке анализируются результаты, разбираются ошибки, после этого проводится урок контрольной работы.
