Программа элективного курса Показательные, логарифмические, иррациональные уравнения и неравенства
| Вид материала | Программа |
- Элективный курс по математике для учащихся 9 класса тема: «уравнения и неравенства,, 248.15kb.
- Программа Элективного курса по математике «Иррациональные уравнения и неравенства», 227.79kb.
- Тематическое планирование элективного курса «Уравнения второй степени и неравенства, 85.14kb.
- Решение нелинейных уравнений, 260.77kb.
- Программа элективного курса для учащихся 11 классов решение уравнений и неравенств, 128.1kb.
- Программа элективного предмета по математике, 57.1kb.
- Урок математики с информатикой по теме «Иррациональные уравнения и неравенства», 43.05kb.
- Элективный курс квадратичная зависимость и связанные с ней уравнения, неравенства, 45.88kb.
- Урок по теме: "Показательные функции, уравнения, неравенства", 69.08kb.
- Приказ № от 2006 г. Программа элективного курса уравнения и неравенства, 161.32kb.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ ТАТАРСТАН
ИНСТИТУТ НЕПРЕРЫВНОГО ПЕДАГОГИЧЕСКОГО ОБРАЗОВАНИЯ
Квалификационная работа
Программа элективного курса
Показательные, логарифмические, иррациональные уравнения и неравенства
Составитель:
Мартынова
Светлана
Васильевна,
учитель математики
МОУ «Открытая (сменная) общеобразовательная школа № 65»
Набережные Челны
2008г
Пояснительная записка
К решению уравнений и неравенств сводятся многие математические задачи – не случайно на протяжении долгого времени считалось, что алгебра – это, прежде всего наука о решении уравнений.
Обучение методам решения уравнений и неравенств традиционно является важнейшей частью школьного курса математики.
Каковы же результаты обучения? Окончившие среднюю школу обычно неплохо владеют техническими навыками решения уравнений и неравенств, однако нередко можно видеть, что, даже получив верный ответ, учащийся не уверен, что решил то или иное уравнение правильно. Связано это с тем, что при решении уравнений и неравенств помимо технических приходится преодолевать и логические трудности и, в частности, отвечать на вопрос, почему выполненные преобразования не приводят к потере корней или приобретению посторонних корней.
Данный элективный курс составлен как дополнительный к типовой программе для открытой (сменной) общеобразовательной школы, работающей по базисному учебному плану года. Курс направлен на обобщение, систематизацию и углубление знаний по теме, традиционно изложенной в действующей программе, но недостаточно представленной в нестандартных заданиях, необходимых для успешной сдачи вступительных экзаменов в ВУЗы или успешного тестирования при сдаче ЕГЭ.
ЦЕЛЬ элективного курса:
Повысить уровень усвоения образовательного стандарта, качества знаний, умений и навыков при решении показательных, логарифмических и иррациональных уравнений и неравенств у учащихся как гарант успешной итоговой аттестации и сдаче ЕГЭ.
ЗАДАЧИ элективного курса:
- Обобщить, систематизировать и углубить знания и умения по теме «Показательные, логарифмические и иррациональные уравнения и неравенства»;
- Развить у учащихся математическую логику, мышление, исследовательские навыки, навыки организации умственного труда и самообразования;
- Воспитать аккуратность при оформлении решений уравнений и неравенств каждого типа.
Курс ориентирован на учащихся, выбравших для себя те области деятельности, в которых математика играет роль аппарата, специфического средства для изучения закономерностей окружающего мира.
Курс рассчитан на 12 часов. Состоит из тем, предусмотренных программой курса с углубленным изучением математики и материала, используемого в тестах ЕГЭ и централизованного тестирования.
В процессе обучения учащиеся систематизируют свои знания по теме «Показательные, логарифмические, иррациональные уравнения и неравенства», с общими методами решения уравнений и неравенств, со специальными и нестандартными методами решения показательных, логарифмических и иррациональных уравнений, неравенств; рассмотрят примеры оформления решения заданий повышенного уровня сложности С5 из ЕГЭ.
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
| № П/П | ТЕМА | Количество часов | В том числе на: | Форма контроля | |
| лекции | практику | ||||
| 1 | Основные понятия, относящиеся к уравнениям и неравенствам | 2 | 1 | 1 | - |
| 2 | Общие методы решения показательных, логарифмических, иррациональных уравнений. Оформление решений каждого типа | 3 | 1 | 2 | - |
| 3 | Специальные методы решения уравнений | 4 | 1 | 2 | Зачет №1, 1 час |
| 4 | Комбинированные уравнения и неравенства | 3 | - | 2 | Зачет №2, 1 час |
| | |||||
| Итого: | 12 | 3 | 7 | 2 | |
СОДЕРЖАНИЕ ОБУЧЕНИЯ
ТЕМА №1. Основные понятия, относящиеся к уравнениям и неравенствам
(2 часа)
Определение уравнения, корень уравнения, область допустимых значений уравнения. Что значит решить уравнение. Допустимые преобразования уравнения. Уравнение – следствие. Равносильные уравнения. Свойства равносильности уравнений. Определение неравенства. Свойства неравенств.
Обобщить, систематизировать знания и умения по теме «Показательные, логарифмические и иррациональные уравнения и неравенства»;
ТЕМА №2. Общие методы решения показательных, логарифмических, иррациональных уравнений. Оформление решений каждого типа
(3 часа)
Основные типы показательных, логарифмических, иррациональных уравнений и неравенств. Способы оформления их решения. Примеры потери корней и приобретения лишних корней.
Углубить знания и умения по теме «Показательные, логарифмические и иррациональные уравнения и неравенства», Воспитать аккуратность при оформлении решений уравнений и неравенств каждого типа.
ТЕМА №3. Специальные методы решения уравнений
(4 часа)
Рассмотреть нестандартные способы решения уравнений и неравенств, оформление заданий повышенного уровня сложности группы С из ЕГЭ.
Развить у учащихся математическую логику, мышление, исследовательские навыки, навыки организации умственного труда и самообразования.
ТЕМА №4. Комбинированные уравнения и неравенства
(3 часа)
Рассмотреть примеры комбинированных уравнений и неравенств, набор методов решения таких уравнений и неравенств, уметь прослеживать все решения заданий и отбирать нужные, исключая побочные решения. Уметь обосновывать свои рассуждения.
ПРАКТИЧЕСКИЕ ЗАДАНИЯ
Задания С2
| 1, 42 | Найдите все значения х, при каждом из которых выражения 3xLog4(3 – 2x) + 4x2Log0,25 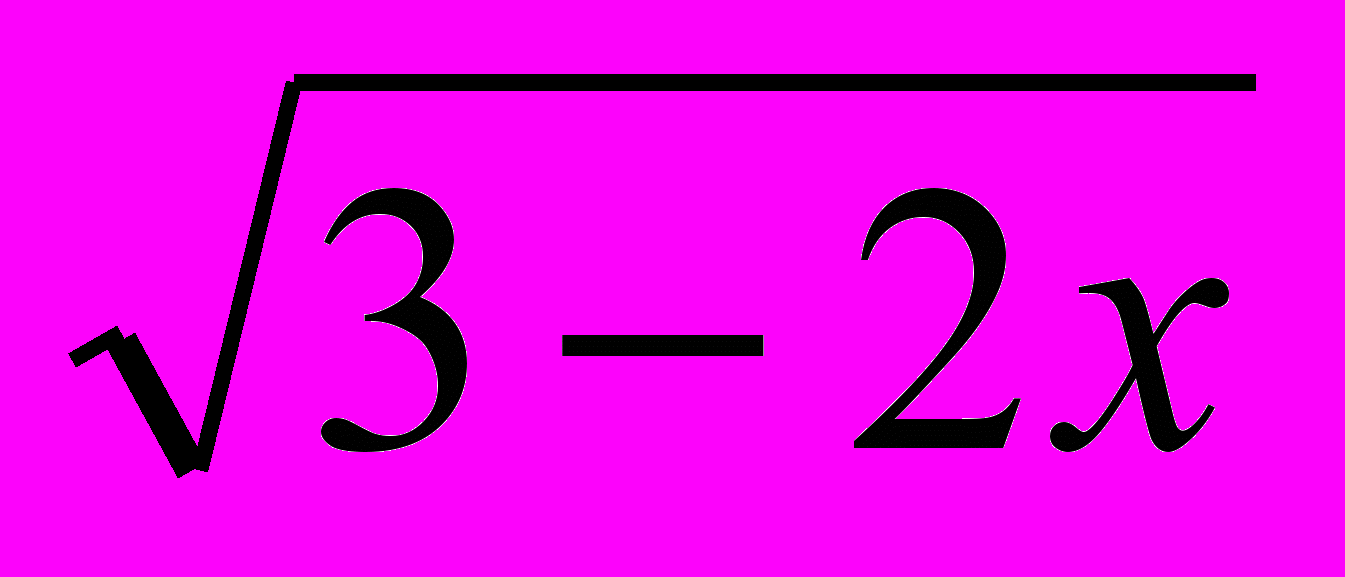 и 3х – 2х2 принимают равные значения. и 3х – 2х2 принимают равные значения. | -0,5; 0 |
| 2, 25 | … 6хLog2 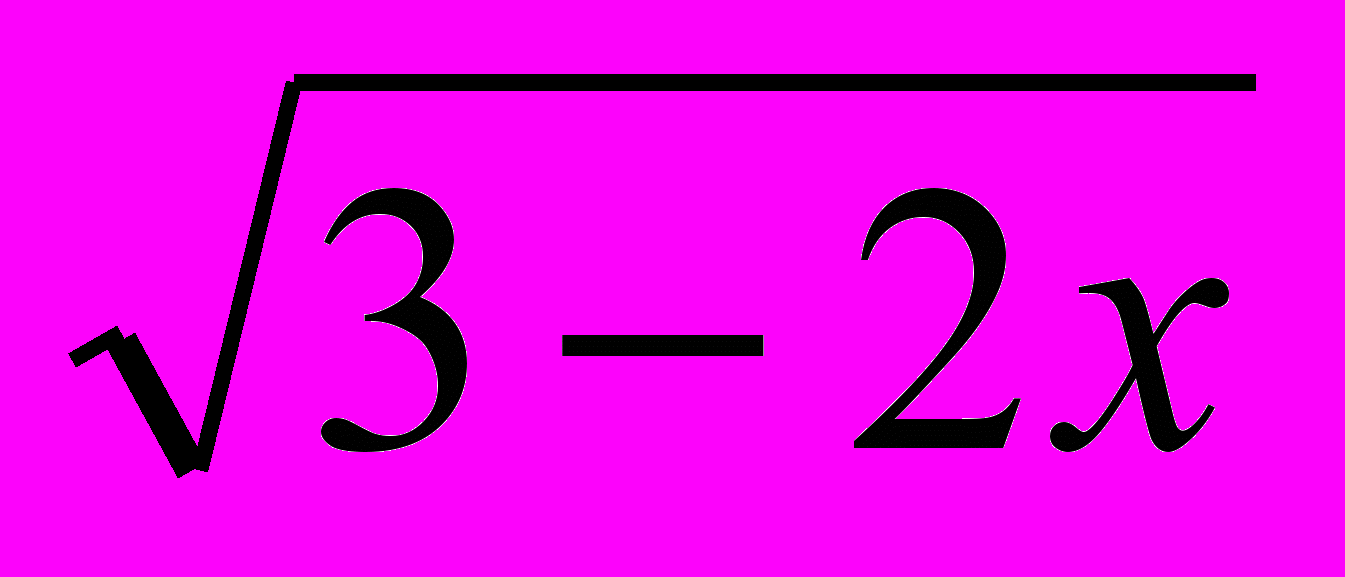 + 2x2Log0,5(3 – 2x) и 2х2 – 3х … + 2x2Log0,5(3 – 2x) и 2х2 – 3х … | 0; 1,25 |
| 3, 26 | … 6х2 Log 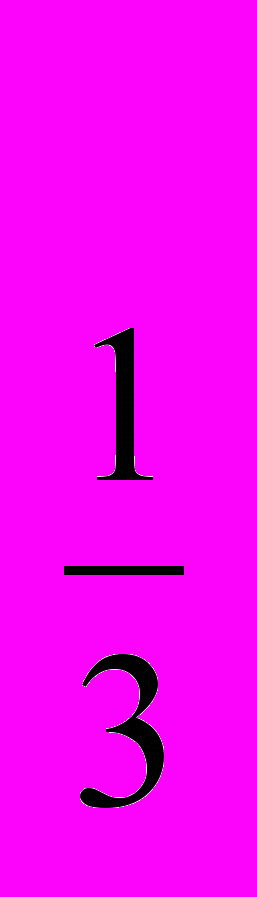 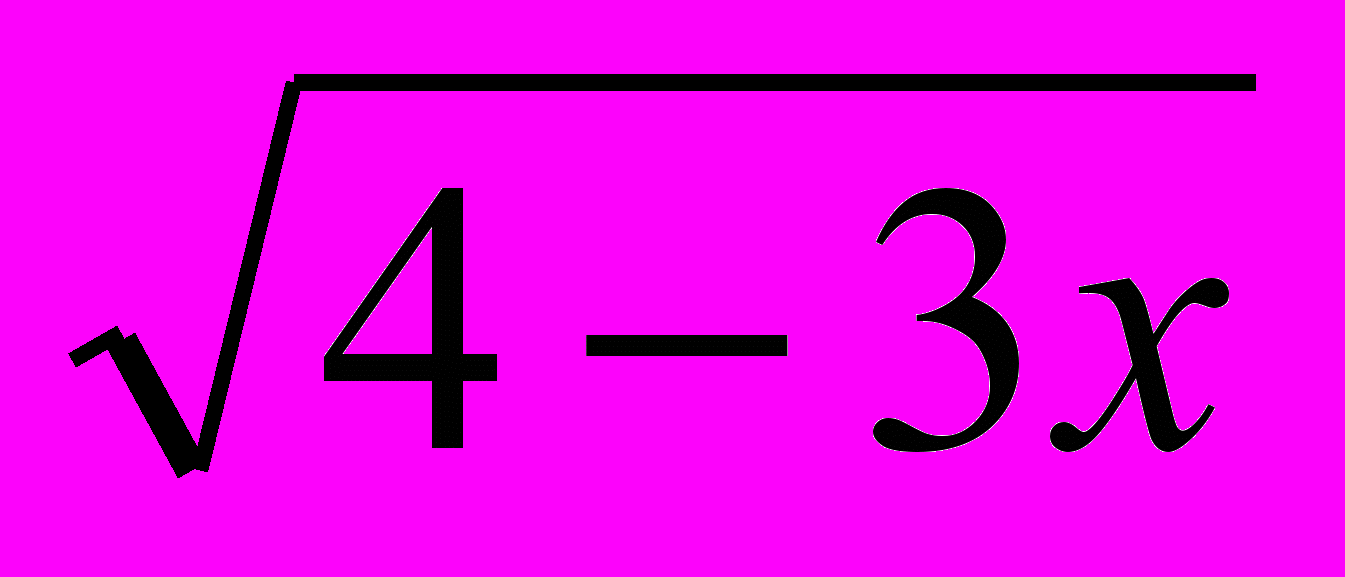 + 4xLog3(4 – 3x) и 4х – 3х2 … + 4xLog3(4 – 3x) и 4х – 3х2 … | 0; 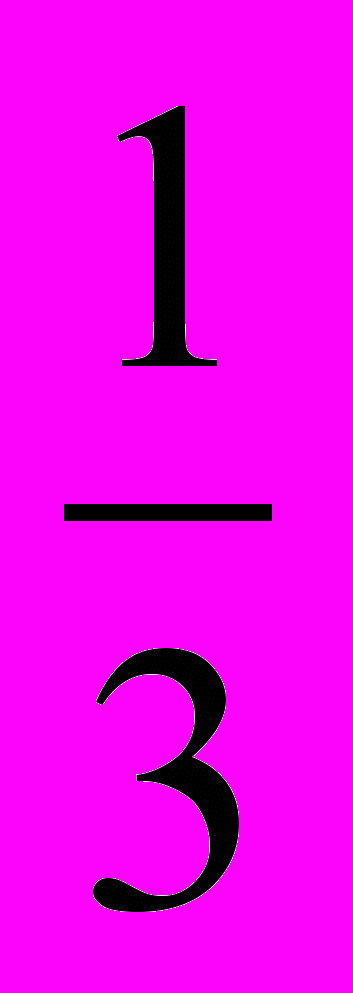 |
| 4, 27 | … 10хLog4 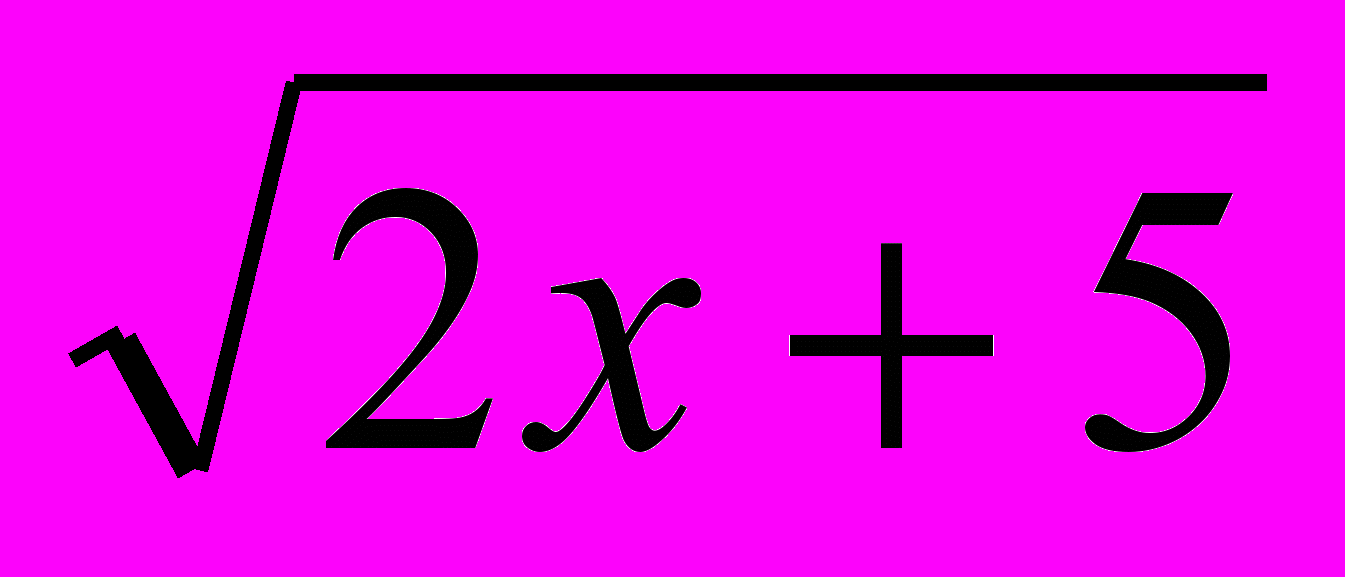 - 2x2Log0,25(2х + 5) и 2х2 + 5х … - 2x2Log0,25(2х + 5) и 2х2 + 5х … | -0,5; 0 |
| 5, 28 | … 5xLog2(3 – 5x) + 9x2Log0,5 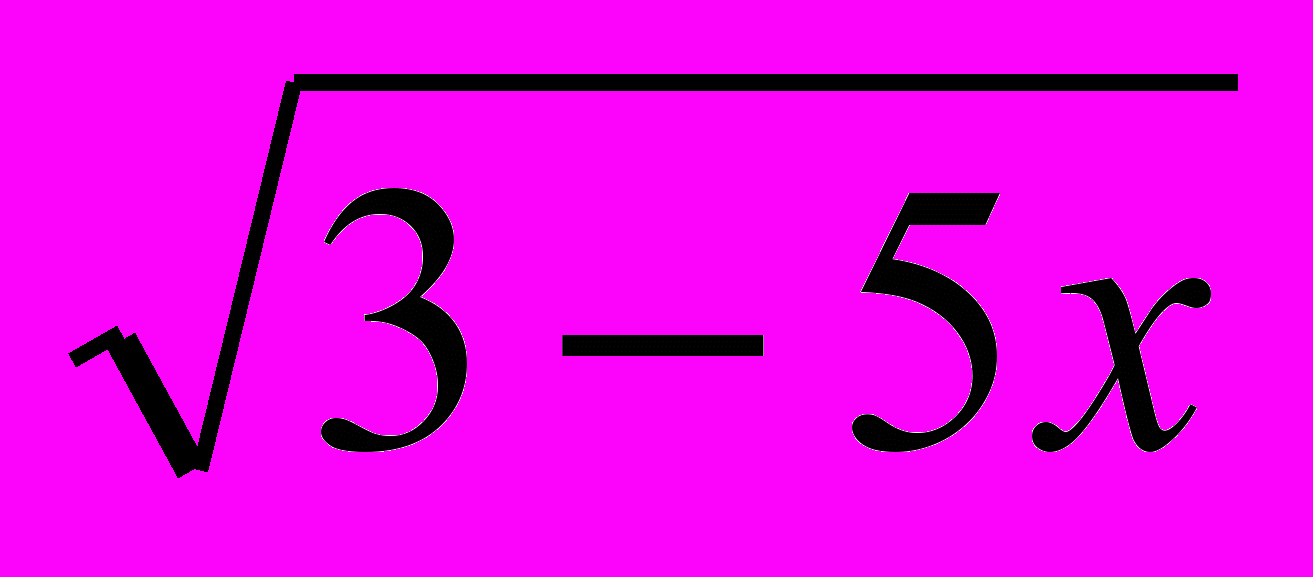 и 5х – 3х2 … и 5х – 3х2 … | 0; 0,2 |
| 6, 29 | … 4x 2 Log3(5 – 4x) + 10xLog 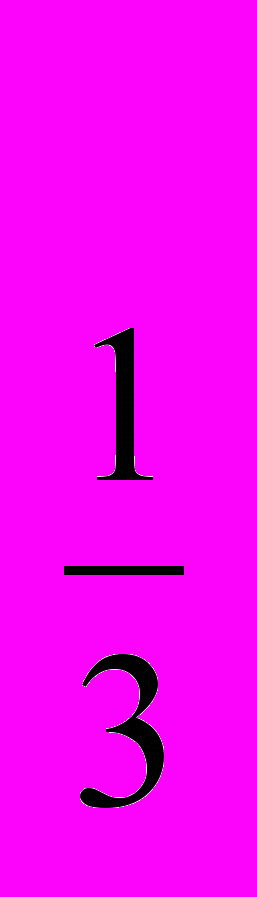 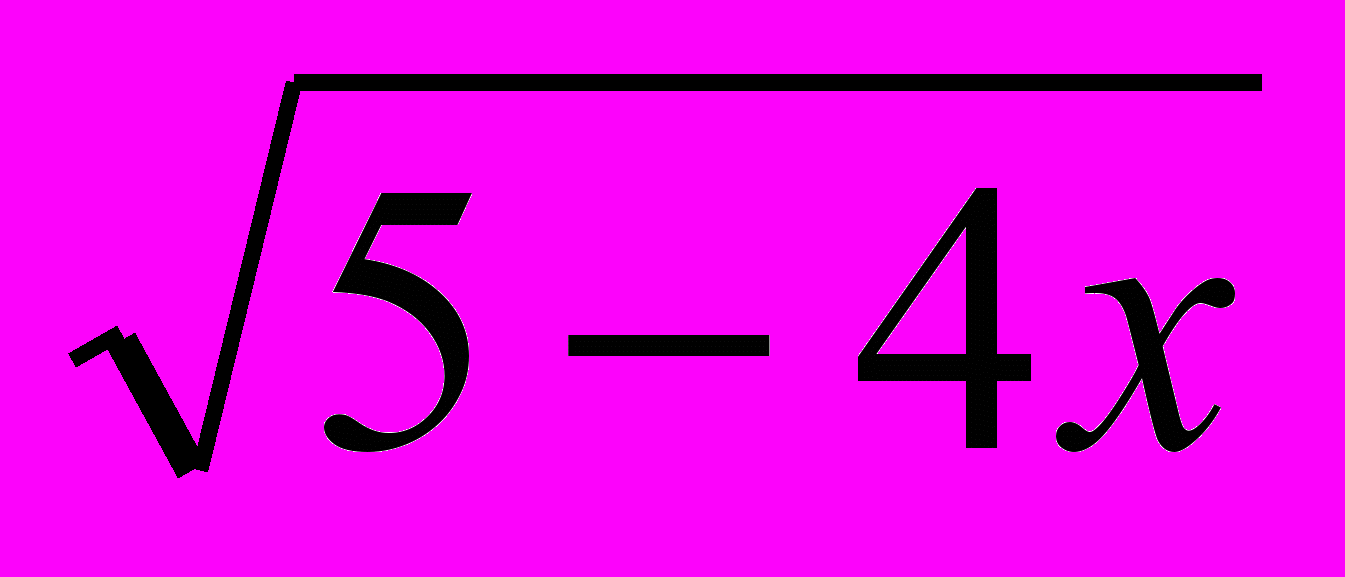 и 4х2 – 5х … и 4х2 – 5х … | 0; 0,5 |
| 13, 30, 54 | … x 2Log2(3х + 1) - xLog0,5  и 3х2 + х … и 3х2 + х … | 0; 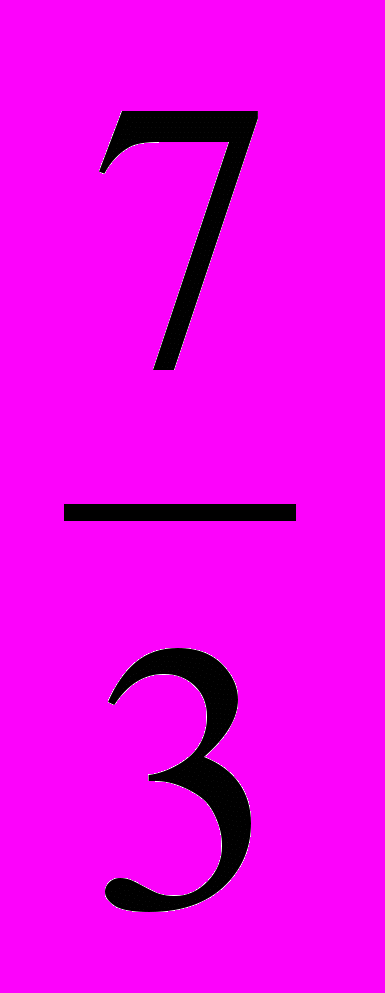 |
| 14, 37, 53 | … xLog2 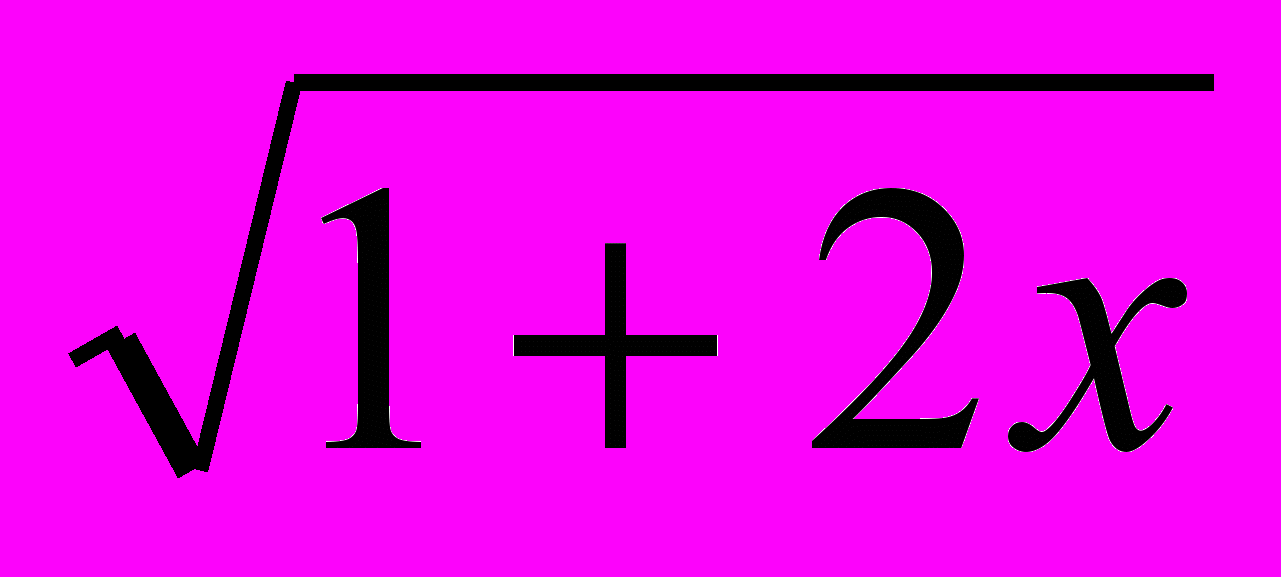 - x 2 Log0,5(1+2х) и 2х2 + х … - x 2 Log0,5(1+2х) и 2х2 + х … | 0; 1,5 |
| 15, 38, 52 | … 8x 2Log 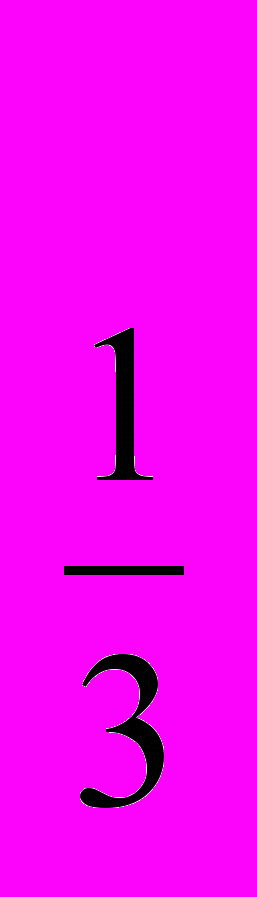 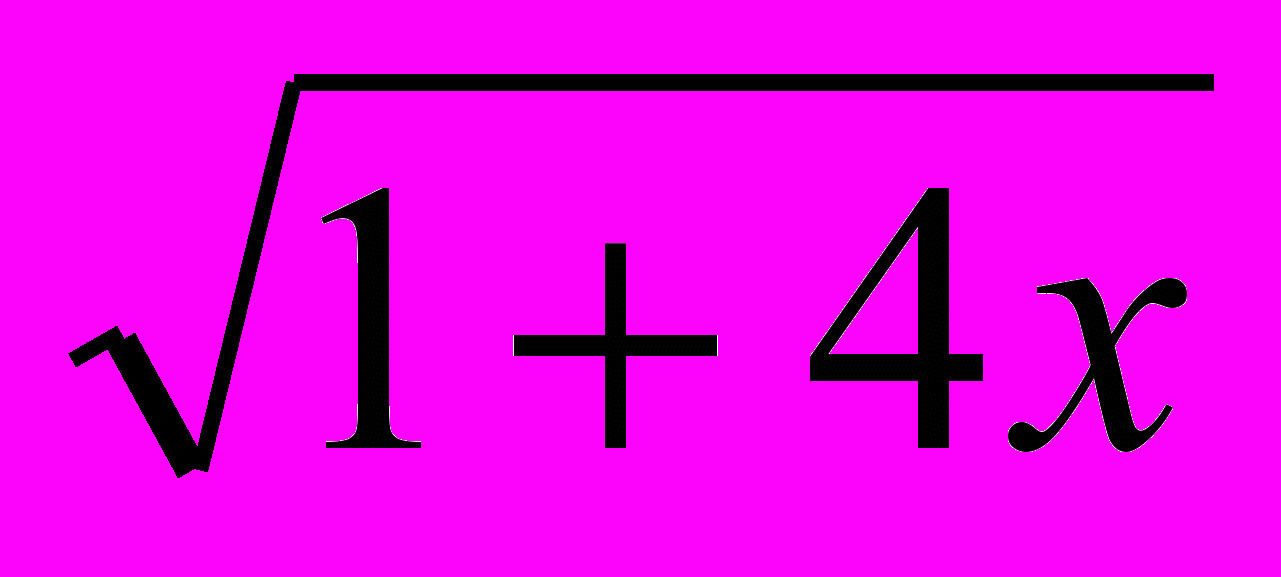 - хLog3(1+4x) и 4х2 + х … - хLog3(1+4x) и 4х2 + х … | - 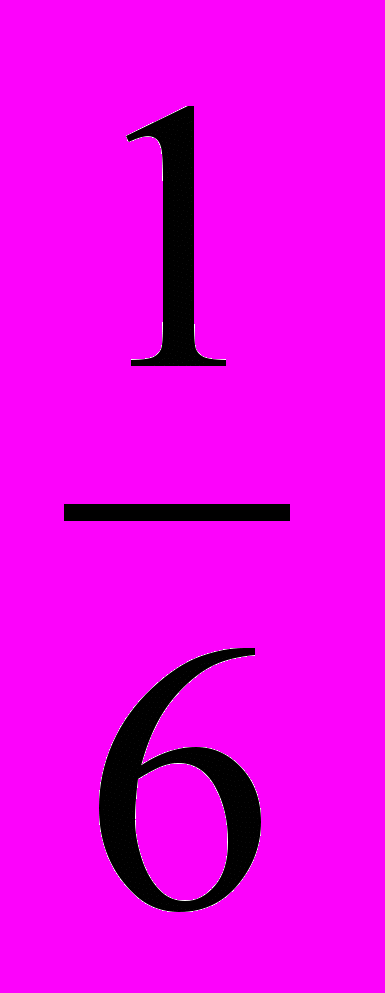 ; 0 ; 0 |
| 16, 39, 51 | … 8хLog5 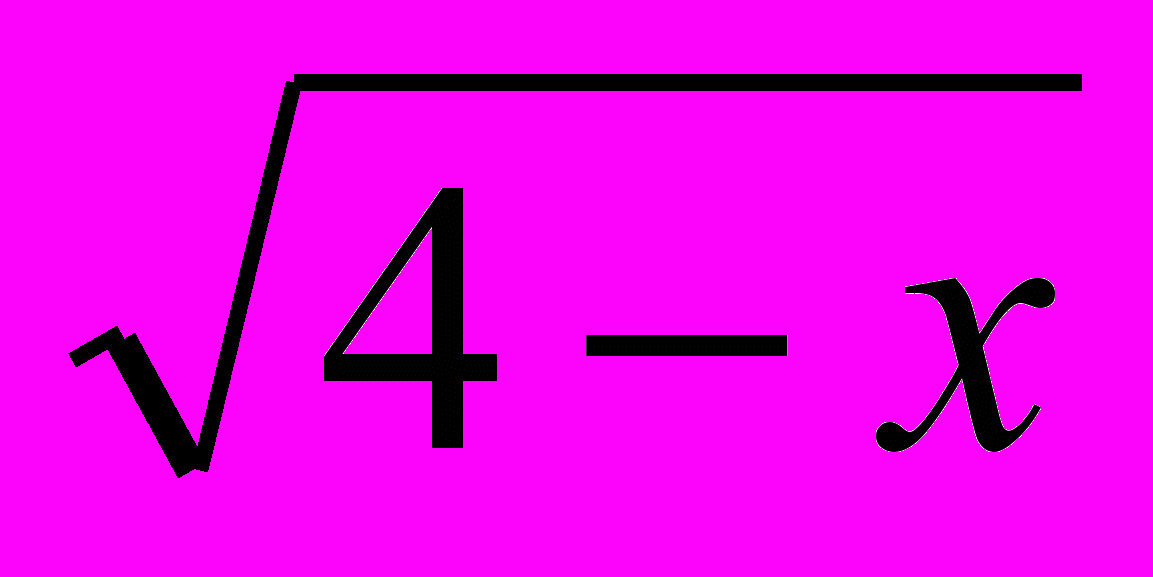 + 4x2Log0,5(4 – x) и х2 – 4х … + 4x2Log0,5(4 – x) и х2 – 4х … | 0; 3,8 |
| 17, 40, 50 | … 6xLog2 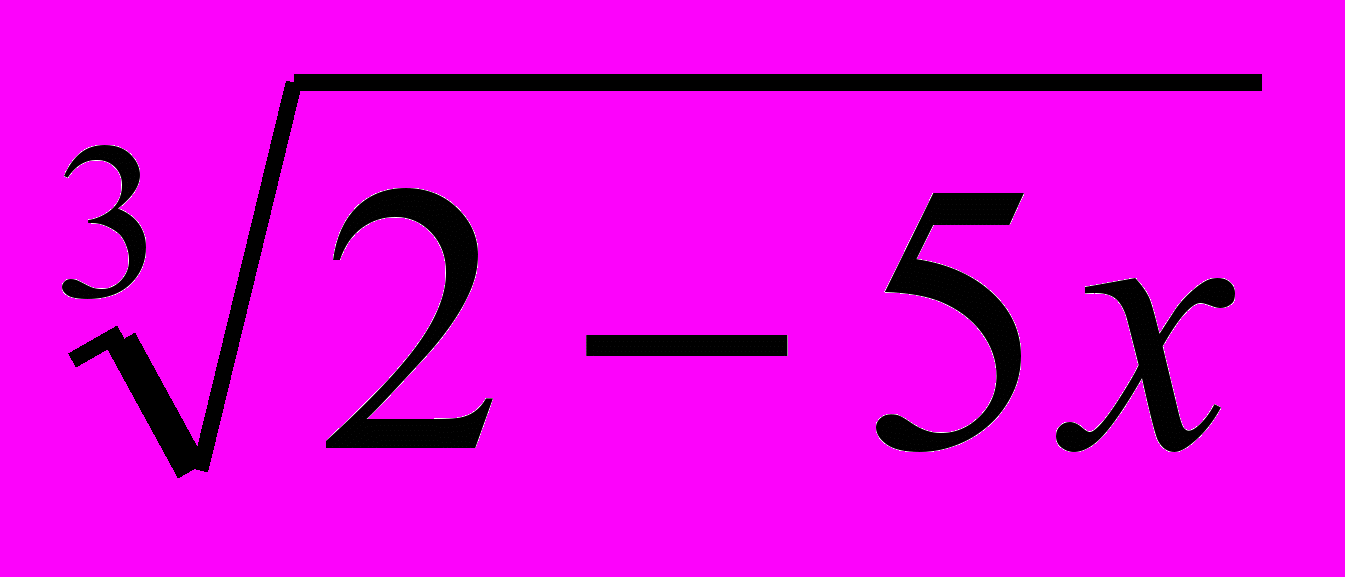 + 5x2Log0,5(2 – 5x) и 5х2 - 2х … + 5x2Log0,5(2 – 5x) и 5х2 - 2х … | 0; 0,3 |
| 18, 41, 49 | … 3x2Log3(2 + 3х) - 6xLog 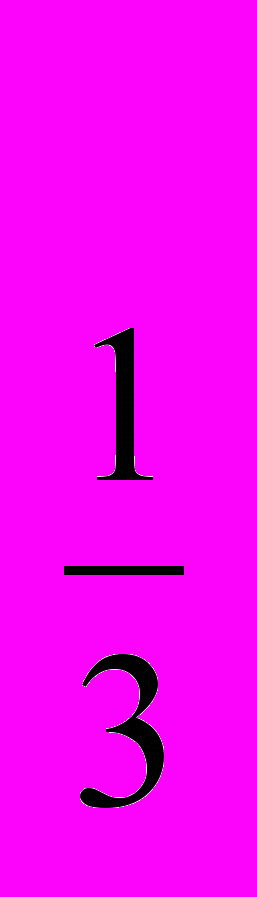 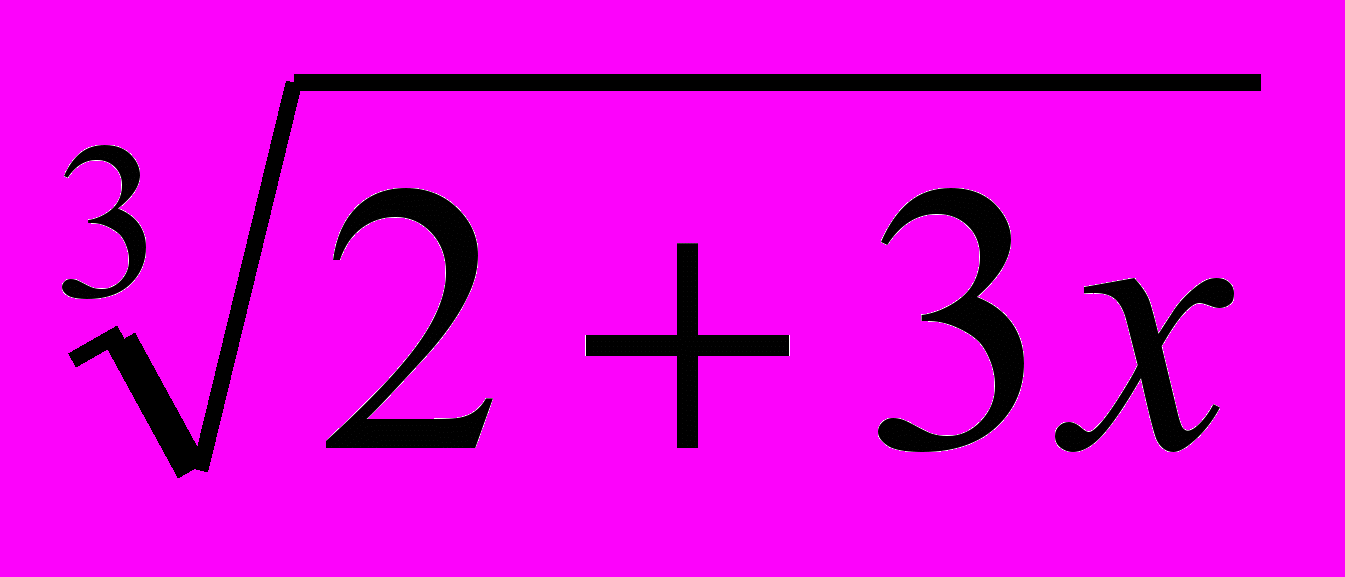 и 3х2 + 2х … и 3х2 + 2х … | 0; 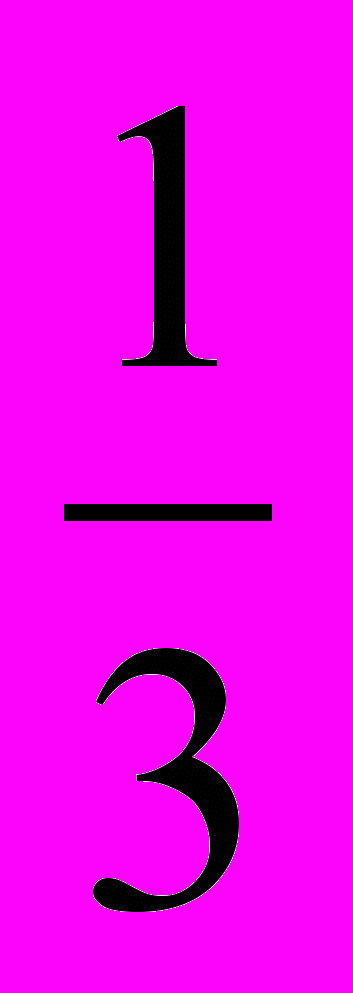 |
Критерии оценки выполнения задания С2
| 2 балла | Приведена верная последовательность всех шагов решения:
Все преобразования и вычисления выполнены верно. Получен верный ответ |
| 1 балл | Приведена верная последовательность всех шагов решения. Допущена описка или вычислительная ошибка в шаге 2), не влияющие на правильность дальнейшего хода решения. В результате этой описки или ошибки может быть получен неверный ответ. |
| 0 баллов | Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1 и 2 балла. |
КОНТРОЛЬ УРОВНЯ ОБУЧЕННОСТИ
Контроль знаний, умений и навыков учащихся является важнейшим этапом учебного процесса и выполняет проверочную, воспитательную и корректирующую функции. Реализация механизма оценки уровня обученности предполагает систематизацию и обобщение знаний, закрепление умений и навыков; проверку уровня усвоения знаний и овладения умениями и навыками, заданными как планируемый результат обучения. При оценке результатов обученности можно использовать систему оценивания В.П. Симонова:
Первый уровень – уровень знакомства (распознавание). На этом уровне обучающийся отличает показательные, логарифмические, иррациональные уравнения и неравенства. Этот уровень знаний учащиеся должны освоить на уроках при и изучении данных тем.
Второй уровень – запоминание. Здесь проверяется способность учащихся воспроизвести содержание изученного курса. Этот уровень, также как и первый, должен быть освоен при изучении базового курса математики, так как соответствует минимальным требования к выпускникам школы.
Третий уровень – предполагает понимание, распознавание существенных признаков и связей между показательными, логарифмическими, иррациональными уравнениями и неравенствами.
Первые три уровня вначале формируются на уроках, а в дальнейшем углубляется и совершенствуется на занятиях элективного курса при изучении темы № 1 «Основные понятия, относящиеся к уравнениям и неравенствам» и темы № 2 «Общие методы решения показательных, логарифмических и иррациональных уравнений и неравенств».
Четвёртый уровень – репродуктивный. Учащиеся должны владеть простейшими умениями и навыками при решении уравнений и неравенств повышенного уровня сложности. Данному уровню соответствует материал темы № 3 «Специальные методы решения уравнений».
Пятый уровень – перенос знаний. Учащиеся способны переложить полученные знания на новую нестандартную ситуацию. Данный уровень хорошо рассматривается и контролируется при изучении темы № 4 «Комбинированные уравнения и неравенства».
Зачет № 1
Часть А
А 1. Корни уравнения √ 3-х = 1 - х есть
А. -2;1. Б. 2. В. 2;-1. Г.-1.
А2. Корни уравнения 7 49Х + 5 14Х = 2 4Х есть
А.0,5. Б. —0,5. В. 1. Г. -1.
А3. Решения неравенства 2Х – 2 3- Х > 2 есть
А. (2;+∞). Б. (-∞;2). В. (-∞;-2)U(1;+∞). Г. (-∞;-1)U(2;+∞).
А4. Корень уравнения logx 8 • log0,5 x/2 = log9 1/27равен
А. 2√2 Б. 1/8. В. 1/4 Г. 4.
А5. Значение выражения -хо 3 - 3хо2 + 2х0 - 5, где хо— корень уравнения 4√х - 0,5х-3 = 0 равно
А. -5. Б. -7. В. -9. Г. -12.
А6. Количество целых решений неравенства равно
А. 1. Б. 2. В. 3. Г. 4.
Часть В
З+2х_х2
В1. Решите уравнение (1о1з(х2 _4)_41о2(х2 _4) = 2
Зачет 2
1 часть
1. Корни уравнения -ъ/х +4- = -4 есть
А. 12;-З. Б. 5;-4. В. 5. Г. 12.
З
2. Решения неравенства 0,5 . >- есть
А. (-со;-0,5). Б. (-со;). В. (+ со). Г. (0,5;+ со).
3. При каком значении а (а>0) корнями уравнения 0,5х = аХ21 являются
числа 1 и 3? Значение а3 тогда равно
А. 1. Б. . В. 2. Г. 8.
х2 + 2х
4. Решением неравенства О есть
1о02(х + 2)
А. (-1;0). Б. (-2;+ со). В. (-2;1)[(0;+ сЮ). Г. (-1;0)1..i(0;+ со).
5. Сумма корней уравнения Со 4х. 1(-х2 + х +2) = О равна
А. 2,т+2. Б. 1+,т. В. 2л-1. Г. 2+7т.
6. Произведение рациональных чисел а и Ь, удовлетворяющих системе [21о42 а —1о4а.1о4Ь _б1О42 Ь = 0,
уравнении равно
[1О2 а + 1ОО5 Ь = 2
А. 64. Б. 27. В. 36. Г. 16.
7. Произведение корней уравнения х21°’ х 81х2 равно
А. 18. Б. 8. В. 3. Г. 1,5.
8. Уравнение х2 — ах = х — а имеет ровно три корня при а
А. а1. Б. а1. В. а—1. Г. а-1.
2 часть
9. Решите уравнение З ‚/iГх +‚(92х _З0.9х +81 = Эх—Э.
ПЕРЕЧЕНЬ РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
- Виленкин Н.Я. и др. Алгебра и математический анализ для 10 класса: Учеб. Пособие для учащихся шк. И классов с углубл. изуч. математики. – М.: Просвещение, 1992.
- Денищева Л.О. и др. Единый государственный экзамен: математика: 2007-2008: контрол. измерит. материалы. – М.: Просвещение, 2007. – 80с.
- Дорофеев Г.В. и др. Сборник заданий для подготовки и проведения письменного экзамена по математике (курс А) и алгебре и началам анализа (курс В) за курс средней школы. 11 класс: Эксперимент. пособие. – М.: Дрофа, 2001. – 160с.
- Ивлев Б.М. и др. задачи повышенной трудности по алгебре и началам анализа: Учеб. пособие для 10-11 кл. ср. шк. – М.: Просвещение, 1990. – 48с.
- Корешкова Т.А. и др. ЕГЭ 2005. Математика. Типовые тестовые задания. – М.: Издательство «Экзамен», 2005. – 80с.
- Корешкова Т.А. и др. ЕГЭ 2007. Математика. Типовые тестовые задания. – М.: Издательство «Экзамен», 2007. – 80с.
- Лаппо Л.Д. ЕГЭ. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ: учебно-методическое пособие/ Л.Д. Лаппо, М.А. Попов, М.: Издательство «Экзамен», 2007.
- Сборник задач по математике для поступающих во втузы: Учеб. пособие под редакцией М.И. Сканави. – М.: Высш. шк., 1993. – 528с.
ЛИТЕРАТУРА
- Базисный учебный план для открытых (сменных) общеобразовательных учреждений РФ (базовая программа для заочных школ).
- Базисный учебный план для образовательных учреждений РФ (программа для углубленного изучения математики).
- Галицкий М.Л. и др. Углубленное изучение курса алгебры и математического анализа: Метод. рекомендации и дидакт. материалы: Пособие для учителя. – М.: Просвещение, 1990. – 352с.
- Корешкова Т.А. и др. ЕГЭ 2007. Математика. Типовые тестовые задания. – М.: Издательство «Экзамен», 2007. – 80с.
- Лаппо Л.Д. ЕГЭ. Математика. Практикум по выполнению типовых тестовых заданий ЕГЭ: учебно-методическое пособие/ Л.Д. Лаппо, М.А. Попов, М.: Издательство «Экзамен», 2007.
- Тесты. Математика. Варианты и ответы централизованного (абитуриентского) тестирования. – М.: ООО «РУСТЕСТ», 2006.
