Программа Элективного курса по математике «Иррациональные уравнения и неравенства»
| Вид материала | Программа |
СодержаниеВведение новой переменной (3) (подстановка) 1.Сколько корней имеет уравнение С.Решите уравнение |
- Элективный курс по математике для учащихся 9 класса тема: «уравнения и неравенства,, 248.15kb.
- Программа элективного курса Показательные, логарифмические, иррациональные уравнения, 113.96kb.
- Программа элективного курса по теме: «Уравнения и неравенства с параметрами», 149.59kb.
- Программа элективного предмета по математике, 57.1kb.
- Тематическое планирование элективного курса «Уравнения второй степени и неравенства, 85.14kb.
- Программа элективного курса для учащихся 11 классов решение уравнений и неравенств, 128.1kb.
- Программа элективного курса по математике «Линейные и квадратные уравнения, системы, 95.45kb.
- Разработаны программы элективных курсов. Программа элективного курса по математике, 98.58kb.
- Урок математики с информатикой по теме «Иррациональные уравнения и неравенства», 43.05kb.
- Элективный курс квадратичная зависимость и связанные с ней уравнения, неравенства, 45.88kb.
МОУ «Средняя общеобразовательная школа № 6»
Согласовано: «Утверждаю»
Руководитель районного Директор школы:
МО учителей математики: /Старостина С. В./
/Денисова А. Е./
Программа
Элективного курса по математике
«Иррациональные уравнения и неравенства»
Автор: Зубова М. Н.,
Учитель математики
1 квалификационной
категории
Г. Кольчугино
Пояснительная записка
Элективный курс «Иррациональные уравнения и неравенства» предназначен для предпрофильной подготовки в 9 классе, своим содержанием сможет привлечь внимание учащихся, которым интересна математика, а также позволит хорошо подготовиться к продолжению обучения в старшей школе и поступлению в высшие учебные заведения. Содержание курса включает материал о различных способах решения (даже нестандартных) иррациональных уравнений и неравенств. Этот курс поможет проанализировать различные подходы к решению. В данном курсе учащиеся знакомятся с решением неравенств обобщенным и эффективным методами, что позволяет быстро и эффективно решать целый класс неравенств повышенной сложности, переводя их тем самым в разряд стандартных задач.
Данный курс рассчитан на 16 часов.
Целью данного элективного курса является: дать учащимся 9-х классов возможность
определиться с выбором профиля дальнейшего обучения в старшей школе, при этом показать значимость знаний по математике.
Для этого необходимо решать задачи:
- создать в совокупности с основными разделами курса базу для развития познавательных и творческих способностей учащихся;
- научить применять полученные знания при выполнении нестандартных заданий;
- ознакомить учащихся с различными способами решения иррациональных уравнений и неравенств;
- повышение самооценки учащимися собственных знаний по математике;
- выработать навыки самостоятельной работы.
Данный элективный курс позволит так же повысить познавательный интерес к предмету и приобрести конкретные практические навыки; перейти от репродуктивного уровня усвоения материала (простого решения уравнений и неравенств) к творческому; научить применять знания при выполнении нестандартных заданий; научить логически мыслить учащихся. Программа элективного курса охватывает и расширяет некоторые изучаемые темы предмета « Алгебра и начала математического анализа» в старшей школе, это позволит подготовить учащихся к продолжению образования.
Ожидаемые результаты обучения:
- точно и грамотно формулировать теоретические положения и излагать собственные рассуждения в ходе выполнения заданий;
- формирование практических навыков по применению способов решения иррациональных уравнений и неравенств;
- умение выбрать соответствующий метод решения иррациональных уравнений и неравенств.
Тематическое планирование ( 16 ч.)
| № | Наименование темы | Форма занятия | Форма контроля |
| 1 | Решение простейших иррациональных уравнений | Лекция. Выполнение тренировочных упражнений | |
| 2 | Решение простейших иррациональных уравнений | Практикум | Самостоятельная работа |
| 3 | Решение более сложных иррациональных уравнений | Лекция | |
| 4 | Решение более сложных иррациональных уравнений | Практикум. Выполнение тренировочных упражнений | |
| 5 | Решение более сложных иррациональных уравнений | Практикум | Тестирование |
| 6 | Нестандартные способы решения иррациональных уравнений | Лекция | |
| 7 | Нестандартные способы решения иррациональных уравнений | Практикум. Выполнение тренировочных упражнений | |
| 8 | Нестандартные способы решения иррациональных уравнений | Практикум | Самостоятельная работа |
| 9 | Нестандартные способы решения иррациональных уравнений | Практикум | Тестирование |
| 10 | Основные свойства и решения иррациональных неравенств | Лекция Выполнение тренировочных упражнений | |
| 11 | Основные свойства и решения иррациональных неравенств | Практикум | Самостоятельная работа |
| 12 | Решение более сложных иррациональных неравенств | Лекция | |
| 13 | Решение более сложных иррациональных неравенств | Практикум. Выполнение тренировочных упражнений | |
| 14 | Решение более сложных иррациональных неравенств | Практикум | |
| 15 | Решение более сложных иррациональных неравенств | Практикум | Защита творческого задания |
| 16 | Итоговый тест | | |
Содержание программы
1.Решение простейших иррациональных уравнений. (2ч.)
Определение иррационального уравнения. Примеры иррациональных уравнений. Свойства, на котором основано решение иррациональных уравнений. Область определения иррационального уравнения. Проверка корней.
2. Решение более сложных иррациональных уравнений. (3 ч. )
Введение подстановки других переменных.. Возведение обеих частей уравнения в третью степень.Решение уравнений, содержащих корень квадратный в корне квадратном. Графическое решение уравнения.
3. Нестандартные способы решения иррациональных уравнений. ( 4 ч. )
Использование систем уравнений при решении. Умножение и деление частей уравнения на выражения, сопряженные знаменателям.
4. Основные свойства и решения иррациональных неравенств. ( 2 ч. )
Область определения неравенства. Основные свойства иррациональных неравенств.
5. Решение более сложных иррациональных неравенств. ( 4 ч. )
Решение неравенства с помощью графика. Применение логического анализа в решении. Применение подстановки.
6. Итоговый тест . ( 1 ч. )
Литература:
- Григорьева Г. И. Задания для подготовки к олимпиадам. Волгоград. «Учитель»,2005
- Кривоногов В. В. Нестандартные задания по математике. М. : « 1 сентября», 2003.
- Шарыгин И. Ф. Факультативный курс по математике 10. М.: « Просвещение». 1989.
- Шахмейстер А. Х. Иррациональные уравнения и неравенства. С- Петербург. 2003.
| Возведение в степень (1) | Уединение радикала (2) | Введение новой переменной (3) (подстановка) | Уравнения, содержащие радикалы (4) |
| Уравнения вида 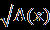 = В(х) равносильно системе, состоящей из уравнения А(Х) = В²(х) и неравенства В(х) = В(х) равносильно системе, состоящей из уравнения А(Х) = В²(х) и неравенства В(х)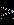 0, то есть: 0, то есть: 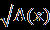 = В(х) = В(х) 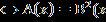 ) )В(х)≥0. Пример1.Решите уравнение 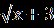 =1. =1.Решение. 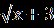 =1. =1.х+3 = 1, 1≥0; ⇔ х= -2. Ответ : -2. Пример2. Решите уравнение 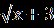 = -1. = -1.Данное уравнение не имеет решения, так как 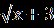 = -1⇔ = -1⇔ х+3=(-1)² -1≥0. Второе условие этой системы не выполняется ни при одном значении х. Ответ: решений нет. Обратим внимание на то, что при этом ОДЗ выполняется автоматически и его можно не писать, а условие В(х)≥0 необходимо проверить. | Смысл таких преобразований в сведении данного иррационального уравнения к рациональному уравнению. Пример1Решите уравнение 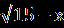 + +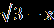 =6. =6.Решение. Найдём О.Д.З. Уединим радикал. 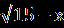 = 6- = 6- 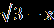 . .Отсюда следует: 15-х≥0, 3-х≥ 0, ⇔ 6 – 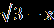 ≥ 0, ≥ 0, х≤15, ⇔ х≤ 3, ⇔ х≥ -33 ⇔ -33 Возведём в квадрат обе части уравнения: 15-х=36-12 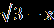 +3-х, +3-х,12 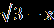 =24. =24. Ещё раз возведём в квадрат обе части уравнения: 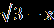 = 2, = 2, ( 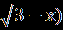 )²=2², )²=2²,3-х=4, х=-1. Найденное значение х удовлетворяет области допустимых значений уравнения, так как –33<-1<3 Ответ: - 1. | В некоторых уравнениях нет необходимости возводить в квадрат обе части, т.к. получившееся уравнение может оказаться громоздким. Здесь лучше сделать замену переменных. Рассмотрим на примере: х²+3х-18+4 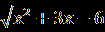 =0. =0.Решение. Обозначим: х²+3х-6=у, тогда у-12 +4  =0, =0,4  =12 – у. =12 – у.О.Д.З. у≥0, 12-у≥0, ⇔ ⇔ у≤12, у≥0,⇔ ⇔ 0≤ у ≤12. У прин [0;12]. Возведём в квадрат обе части уравнения, получим 16у = 144- 24у + у², у² - 40у +144 =0, у1= 36, у2=4. у1 =36 не прин [0;12]. Значит: х² +3х – 6=4, х² +3х-10 = 0, Д=49, х1=-5, х2 = 2. Ответ -5; 2. | Основной метод решения таких уравнений является последовательное возведение в квадрат обеих частей уравнения, используя формулы сокращенного умножения. (а+в)³ = а³+в³ +3ав(а+в), (а-в)³ = а³-в³ - 3ав(а-в). Пример. 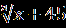 - - 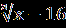 =1. Решение. 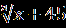 - - 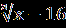 = 1, = 1,( 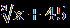 - - 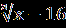 )³ =1³, )³ =1³,(х+45) –(х-16) – 3(х+45)(х-16) 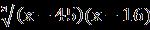 =1. =1.По условию: 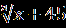 - - 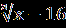 =1. =1.Тогда: х+45- х +16 - 3 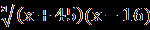 =1, =1,3 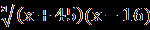 = 60, = 60,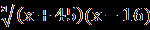 =20, =20,(х+45)(х-16)=8000, х² + 29х -8720 =0, х1=80, х2 = - 109. Ответ: -109; 80. |
Карточки для самостоятельной работы.
Карточки уровня А.
| Вариант 1 | | Вариант 2 |
х+ 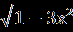 = 0 = 0Ответ: - 0,5. 2. 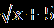 = х+2 = х+2Ответ: 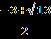 . . | | 1.Решите уравнение: -1 = х – 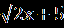 Ответ: 2. 2.1-2х+3  = 4 = 4Ответ: 0. |
Проверочный лист
Вариант №1.
Решение. х+ 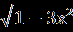 =0. =0.Изолируем квадратный корень от других членов уравнения, получим: 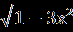 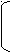 = - х,⇒ 1-3х²=х², ⇒ 4х²=1,⇒ х²= = - х,⇒ 1-3х²=х², ⇒ 4х²=1,⇒ х²=  ,⇒ х= ,⇒ х=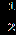 , ,х= -  . Проверка. 1) х= . Проверка. 1) х=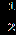 , ,  + + 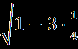 =0 ⇒ =0 ⇒  + + = 1⇒ 1≠0, неверн0, х= = 1⇒ 1≠0, неверн0, х= - не является корнем исходного уравнения. - не является корнем исходного уравнения.2)х= -  ,- ,-  + + 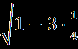 = 0,⇒ 0=0,верно, х= - = 0,⇒ 0=0,верно, х= -  - корень исходного уравнения . Ответ: - - корень исходного уравнения . Ответ: -  . .2. 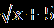 = х+2. = х+2.Решение. 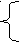 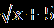 = х+2. Перейдём к равносильной системе (х+5)=(х+2)², = х+2. Перейдём к равносильной системе (х+5)=(х+2)²,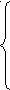 х+2≥0; х+2≥0;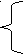 х≥ - 2. х≥ -2, х≥ - 2. х≥ -2,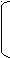 х²+3х-1 = 0; х= х²+3х-1 = 0; х= 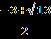 , ,х= 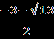 ; х= ; х= 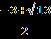 . .Ответ : 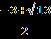 . . |
Проверочный лист.
| Вариант 2. |
Решение. - 1 = х – 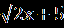 . .Изолируем квадратный корень от других членов уравнения, получаем: 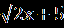  =х + 1,⇒ 2х+5=(х+1)²,⇒ х²=4,⇒ х=2, =х + 1,⇒ 2х+5=(х+1)²,⇒ х²=4,⇒ х=2,х= - 2. Проверка. 1) х=2, -1 = 2 - 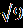 ⇒ - 1 = 2 – 3 ⇒ - 1 = - 1 –верно, х=2 – корень исходного уравнения. ⇒ - 1 = 2 – 3 ⇒ - 1 = - 1 –верно, х=2 – корень исходного уравнения.2)х= - 2, - 1 =- 2 - 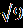 ,⇒ - 1 ≠ -3 – неверно, х = - 2- не является корнем исходного уравнения. ,⇒ - 1 ≠ -3 – неверно, х = - 2- не является корнем исходного уравнения.Ответ: 2.
Решение.
Выполним замену. Пусть  =у, у≥0, тогда получим уравнение =у, у≥0, тогда получим уравнениеу² + 3у – 4 =0. По теореме Виета у1=1, у2= -4. Значение у2= -4 не удовлетворяет условию у≥0. Восстанавливаем замену:  = 1; 1-2х=1; х=0. = 1; 1-2х=1; х=0.Ответ: 0. |
Карточки уровня В.
| Вариант1 | | Вариант 2 |
| 1.Решите уравнение 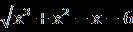 = х. = х.Ответ: 2. 2.Найдите сумму корней уравнения 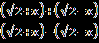 = = . .Ответ: 0. | | 1.Сколько корней имеет уравнение 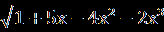 = 2х+1? = 2х+1?Ответ: 2. 2.Найдите количество целых решений уравнения 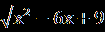 + + 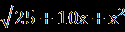 =8. =8.Ответ:9. |
Проверочный лист .
Вариант 1.
1.Решите уравнение
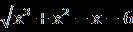 =х.
=х.Решение.
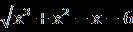 =х.
=х.Воспользуемся условием равносильности.
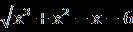
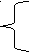
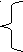 =х⇔ х≥ 0, х≥ 0,
=х⇔ х≥ 0, х≥ 0,х³-х-6 = 0⇔ (х-2)(х²+2х+3)=0⇔ х=2.
Ответ:2.
2.Найдите сумму корней уравнения
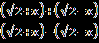 =
=  .
.Решение.
Найдём ОДЗ уравнения:
2
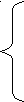 +х ≥0,
+х ≥0,2 – х ≥ 0,
х ≠ 0, ⇒
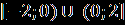
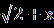 +
+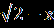 ≠0
≠0Умножим числитель и знаменатель левой части на
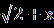 +
+ 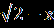 , тогда получим уравнение
, тогда получим уравнение 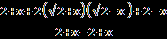 =
=  ,
,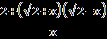 =
=  .
.Умножим обе часть уравнения на х, получаем 2+
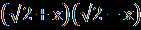 =2.
=2.Корни этого уравнения х1=-2, х2=2.
Подстановкой в исходное уравнение найденных корней устанавливаем, что они найдены верно.
Ответ: х1+х2=0.
| Вариант 2 |
| 1.Сколько корней имеет уравнение 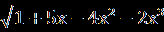 =2х+1? =2х+1?Решение. Воспользуемся условием равносильности, получаем: 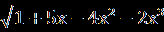 =2х+1⇔ 2х+1≥ 0, х≥ - =2х+1⇔ 2х+1≥ 0, х≥ -  , ,1+5х-4х²-2х³= 4х²+ 4х+1⇔ х(2х²+8х-1)=0⇔ х ≥ - 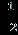 , ,х=0, ⇔ х=0, х= 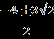 х= х= 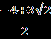 . .Таким образом, уравнение имеет два решения. Ответ: 2. 2.Найдите количество целых решений уравнения 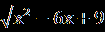 + +  =8. =8.Решение. Заметим, что х² -6х + 9= (х-3)², х²+ 10х +25 = (х +5)², тогда 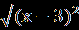 + +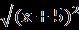 =8; вспомним, что =8; вспомним, что 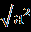 = |a|. = |a|.|x-3| + |x+5|=8, 1 11 111 - 5 3 х 1 х<-5 11 -5≤ х ≤ 3 111 х> 3 3-2х-5-8=0 3-х+х+5=8 х-3+х+5=8 х< -5, -5 ≤ х ≤ 3 х> 3 х= -5. ⊘ 8 = 8. х=3. ⊘ Значит, -5≤ х ≤ 3 - решение исходного уравнения. Найдём целые решения уравнения: -5 -4 -3-2-10 1 2 3 х • • • • • • • • • Всего девять целых решений уравнения. Ответ: 9. |
Карточки уровня С.
| Вариант 1 | Вариант 2 |
| 1.Решите уравнение 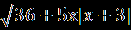 = x+6. = x+6.2.Решите уравнение 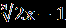 + +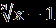 =1. =1. | 1.Решите уравнение 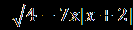 =3x+2. =3x+2.2.Решите уравнение 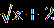 - - 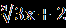 =0. =0. |
| Проверочный лист. Вариант 1.
Решение. Рассмотрим совокупность двух смешанных систем х   +3≥0, +3≥0,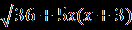 =х+6, (1) =х+6, (1) х+3< 0, 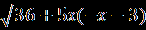 =х+6. (2) =х+6. (2)Решим каждую систему отдельно, а полученные множества объединим. Система (1). х    +3 ≥ 0, х≥ -3, х≥ -3, +3 ≥ 0, х≥ -3, х≥ -3,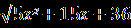 =х+6; ⇒ х+6 ≥ 0, ⇒ 4х²+3х =0; ⇒ =х+6; ⇒ х+6 ≥ 0, ⇒ 4х²+3х =0; ⇒5х²+15х+36=х²+12х+36; 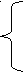 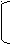 х≥ -3, х=0, х≥ -3, х=0,⇒ 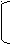 х=0, ⇒ х=- 0,75. х=0, ⇒ х=- 0,75.х= - 0,75; Система (2).    х< -3, х< -3, -6≤ х ≤-3, х< -3, х< -3, -6≤ х ≤-3,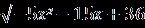 = х+6; ⇒ х+6 ≥ 0, ⇒ 6х²+27х=0; = х+6; ⇒ х+6 ≥ 0, ⇒ 6х²+27х=0;-5х²-15х+36 = х²+12х+36; |
 -6 ≤ х ≤-3,
-6 ≤ х ≤-3,⇒
 х=0, ⇒ х= - 4,5.
х=0, ⇒ х= - 4,5.х=- 4,5;
Ответ: - 4,5; - 0,75; 0.
2.Решите уравнение
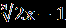 +
+ 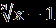 = 1.
= 1.Решение.
После возведения в куб обеих частей уравнения, получаем
3х-2+3
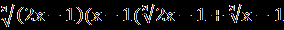 )=1.
)=1.Напоминаем: (х+у)³=х³+ 3х²у+3ху³ +у³ = х³+у³ + 3ху(х+у).
Выражение, стоящее в скобках, заменим на 1.
Полученное уравнение 3х-2 +3
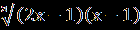 =1 возведём в куб, уединяя радикал. Получим уравнение х²(х-1)= 0.
=1 возведём в куб, уединяя радикал. Получим уравнение х²(х-1)= 0.Корни этого уравнения х1=0, х2 = 1 подставим в исходное уравнение и убедимся, что только х=1 является его корнем.
Ответ: х=1.
Вариант 2.
- Решите уравнение
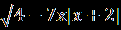 = 3х+2.
= 3х+2.
Решение.
Так как левая часть уравнения не отрицательна, то 3х+2 ≥ 0, то есть х≥ -
 .
.Тогда
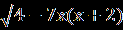 = 3х+3,
= 3х+3,4 – 7х(х+2)= 9х² +12х+4,
4 – 7х²- 14х= 9х² + 12х+4,
8х² + 13=0,
х1 = 0; х2 = -
 .
.х2 - не удовлетворяет требованию х≥ -
 .
.Проверкой убедимся, что не допустили ошибку в решении.
Ответ: 0.
- Решите уравнение
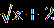 -
- 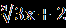 =0.
=0.
Решение.
Запишем уравнение в виде
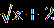 =
= 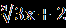 .
.Поскольку левая часть уравнения не может принимать отрицательные значения, то правая часть должна быть неотрицательной. Переходим к равносильной системе:
(
 х+2)³ = (3х+2)², х³- 3х²+4 =0, х³ +1 –(3х²-3)=0,
х+2)³ = (3х+2)², х³- 3х²+4 =0, х³ +1 –(3х²-3)=0, 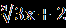
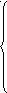 ≥ 0; ⇒ 3х+2 ≥ 0; ⇒ х≥ -
≥ 0; ⇒ 3х+2 ≥ 0; ⇒ х≥ -  ; ⇒
; ⇒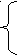
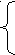
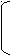 (х+1)(х²-х+1)-3(х+1)(х-1)=0, (х+1)(х²-4х+4)=0, х= - 1,
(х+1)(х²-х+1)-3(х+1)(х-1)=0, (х+1)(х²-4х+4)=0, х= - 1,⇒ х≥ -
 ; ⇒ х≥ -
; ⇒ х≥ -  ; ⇒ х+ 2, ⇒ х=2.
; ⇒ х+ 2, ⇒ х=2.х ≥ -
 ;
;Ответ: 2.
Итоговый тест «Иррациональные уравнения».
| Вариант 1. | Вариант 2. |
| А1.Решите уравнение 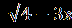 = -х. = -х.А2. Найдите 1+2х0, где х0- корень уравнения 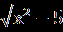 – – 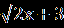 =0. =0.А3.Найдите абсциссу точки пересечения графика функции у= 1+х+ 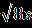 с прямой у=7. с прямой у=7.В. Решите уравнение 19 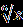 +2 +2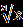 -10=0 и укажите, сколько корней принадлежит отрезку -10=0 и укажите, сколько корней принадлежит отрезку 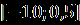 . .С. Решите уравнение 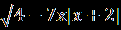 =3x+2. =3x+2. | А1.Найдите сумму корней уравнения 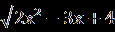 =3. =3.А2.Решите уравнение 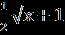 =х-2. =х-2.А3.Найдите абсциссы всех общих точек графиков функций у=5х и у=  . .В.Решите уравнение 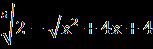 = -1 и определите, сколько корней принадлежит отрезку = -1 и определите, сколько корней принадлежит отрезку 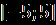 . .С.Решите уравнение 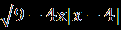 -4х=3. -4х=3. |
| Вариант 3. | Вариант 4 |
| А1.Решите уравнение 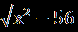 = = 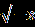 . .1)7;-8 2) -8 3) 7 4) -7;8. А2.Пусть х0- корень уравнения 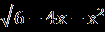 -4=х. Найдите 3х0+1. -4=х. Найдите 3х0+1.1)-2 2) -14 3) 7 4) 16 А3.Укажите абсциссы общих точек графиков функций у= 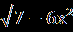 и у=х. и у=х.
В.Найдите сумму корней уравнения (х²-5х-6) 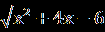 =0. =0.С.Решите уравнение 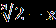 = 1- = 1-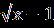 . . | А1.Решите уравнение 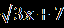 -3=х. -3=х.1)1;2 2) -1;-2 3) -1;2 4)1;-2 А2.Решите уравнение х-1 = 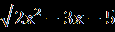 . .1)-3;2 2) 3;-2 3) -3;-2 4) 3 А3.Укажите абсциссы общих точек графиков функций у= 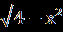 и у=х. и у=х.1) 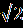 2) - 2) -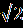 3) 2 4)-2. 3) 2 4)-2.В.Найдите корень уравнения или сумму его корней, если их несколько 5+ 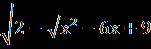 = х. = х.С. Решите уравнение 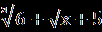 + +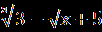 =3. =3. |
| Вариант 5 | Вариант 6. |
| А1.Решите уравнение 6+ 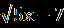 = 2. = 2.1)корней нет 2)4,6 3)-4,6 4) 16 А2.Найдите наибольший корень уравнения (3- 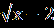 )(4- )(4-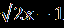 )=0. )=0.1)11 2)8,5 3)27 4)- 13. А3.Найдите абсциссы общих точек графиков функций у=  и у=х. и у=х.
В.Найдите корень уравнения или сумму корней, если их несколько: 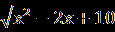 = | 2x+1|. = | 2x+1|.С.Найдите корни уравнения 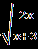 + +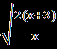 = = 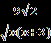 . . | А1.Решите уравнение 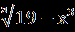 = 3. = 3.1)-2 2) 2 3) 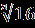 4) -2;2 4) -2;2А2.Найдите наименьший корень уравнения (2- 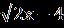 )( )(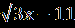 -2)=0 -2)=01)4 2)5 3) – 4 4) 2. А3.Укажите сумму абсцисс графиков функций у= 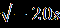 и иу= 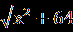 . .1)20 2) -16 3) -20 4) -4. В. Найдите среднее арифметическое корней уравнения 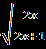 + +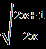 = =  . .С.Решите уравнение 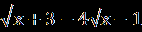 + + 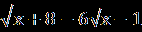 =1. =1. |
Таблица ответов к итоговому тесту.
| № | №задания № варианта | А1 | А2 | А3 | В | С |
| 1 | Вариант 1 | -4 | 9 | 2 | 1 | 0 |
| 2 | Вариант 2 | 1,5 | 3 | 0,25 | 2 | 0 |
| 3 | Вариант 3 | 2 | 1 | 3 | 4 | 1;2;10 |
| 4 | Вариант 4 | 3 | 1 | 4 | 8 | -1 |
| 5 | Вариант 5 | 1 | 1 | 1 | -2 | -6;3 |
| 6 | Вариант 6 | 1 | 1 | 3 | 0 | 5;10 |
Бланк ответов.
| Вариант № | Вариант № | ||||||||
| А1 | А2 | А3 | В | С | А1 | А2 | А3 | В | С |
| | | | | | | | | | |

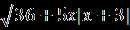 =х+6.
=х+6.