Программа элективного предмета по математике

Вид материала

Программа

Содержание Основная цель Общеучебные умения, навыки и способы деятельности Тематическое планирование Уравнения, содержащие абсолютные величины. Содержание курса 2.2. Метод равносильного перехода к совокупности двух систем неравенств. 2.3. Логический и графический методы решения неравенств с модулями. 2.4. Итоговое тестирование.

Подобный материал:

• Разработаны программы элективных курсов. Программа элективного курса по математике, 98.58kb.
• Программа элективного курса по математике 11 класс, 143.18kb.
• Медведева Нина Петровна 2011-12 учебный год программа, 88.26kb.
• Рабочая учебная программа по математике Класс, 104.32kb.
• Программа элективного курса по математике, 59.86kb.
• Программа элективного курса по теме: «Уравнения и неравенства с параметрами», 149.59kb.
• Рабочая программа учебного предмета «Математика», 824.49kb.
• Муравьева Инна Николаевна Р. п. Дмитриевка-2007 программа курса, 146.99kb.
• Программа элективного курса по математике для учащихся 9 11 классов «Клуб знатоков, 51.57kb.
• Программа элективного курса по математике для учащихся 10 11 классов (68 часов, 2 года,, 118.36kb.

Учебная программа элективного предмета по математике

10. 
    класс
    

Уравнения и неравенства с модулем


Разработан учителем

математики

МОУ Большелиповицкая СОШ

Тамбовского района

Тамбовской области

Блащук Л.В.

2006-2007

учебный год

Пояснительная записка


Элективный курс «Уравнения и неравенства с модулем» рассчитан на 17 часов для учащихся 10 класса. Курс рассматривается в Ι полугодии. Программа содержит два блока, связанных единой идеей. 1 блок (9 часов) – «Уравнения, содержащие абсолютные величины».

2 блок (8 часов) – «Неравенства, содержащие абсолютные величины».

Тема, предложенная в элективном курсе, важна, т.к. связана практически со всеми разделами школьной программы. Задачи с абсолютными величинами встречаются часто на математических олимпиадах и на ЕГЭ. В этом курсе рассматриваются: примеры решения уравнений и неравенств, содержащих знак модуля; способы решения, которые позволяют очень быстро и рационально решить многие уравнения; приемы построения графиков функций, аналитическое выражение которых содержит знак модуля, с помощью преобразований. Приводятся примеры построения на плоскости множеств точек, координаты которых удовлетворяют уравнениям и неравенствам, содержащим знак модуля. Эти приемы являются общими и применяются к уравнениям неравенствам различного вида.

Курс непосредственно связан с материалом базового курса по математике. Он предусматривает доведение изучаемого материала до уровня, на котором учащемуся становится ясной его математическая зависимость, знакомит учащихся с нестандартными методами решения задач повышенной сложности.

Основная цель курса – расширить представление о уравнениях и неравенствах с модулем, овладеть системой знаний и умений, необходимых для решения уравнений и неравенств с модулями, показать общекультурную роль математики, её целостность, формировать качества мышления, характерные для математической деятельности и необходимые для продуктивной жизни в обществе.

Общеучебные умения, навыки и способы деятельности

В ходе освоения содержания элективного курса учащиеся приобретают и совершенствуют опыт:

• решения уравнений и неравенств с модулем аналитическим методом;
  
• решения уравнений и неравенств с модулем с помощью графиков;
  
• самостоятельной работы с источниками информации: учебной и справочной литературой;
  
• ясного и грамотного изложения своих мыслей в устной и письменной речи, с использованием различных языков математики (словесного, символьного и графического).
  

В качестве основания для итоговой аттестации служит:

• подготовка нескольких небольших сообщений, дополняющих лекционный материал;
  
• итоговое тестирование.
  

Тематическое планирование

Блок	Тема	Кол-во часов	Форма занятия
1	Уравнения, содержащие абсолютные величины. Решение уравнений с модулем методом промежутков. Метод равносильного перехода к совокупности двух смешанных систем. Геометрическая интерпретация модуля в задачах. Логический и графический методы решения уравнений с модулем.	3 2 2 2	Лекция, практикум Практикум Семинар Практикум
2	Неравенства, содержащие абсолютные величины 2.1. Метод промежутков. 2.2. Метод равносильного перехода к совокупности двух систем неравенств. 2.3. Логический и графический методы решения неравенств с модулями. 2.4. Итоговое тестирование.	3 2 2 1	Лекция, практикум Практикум Практикум практикум
	ИТОГО:	17

Содержание курса

1. Уравнения, содержащие абсолютные величины
   

Рассматриваются стандартные аналитические и графические методы решения уравнений с переменной под знаком модуля.

1. Решение уравнений с модулем методом промежутков.
   

Модуль действительного числа и его свойства. Сущность метода промежутков. Решение уравнений вида

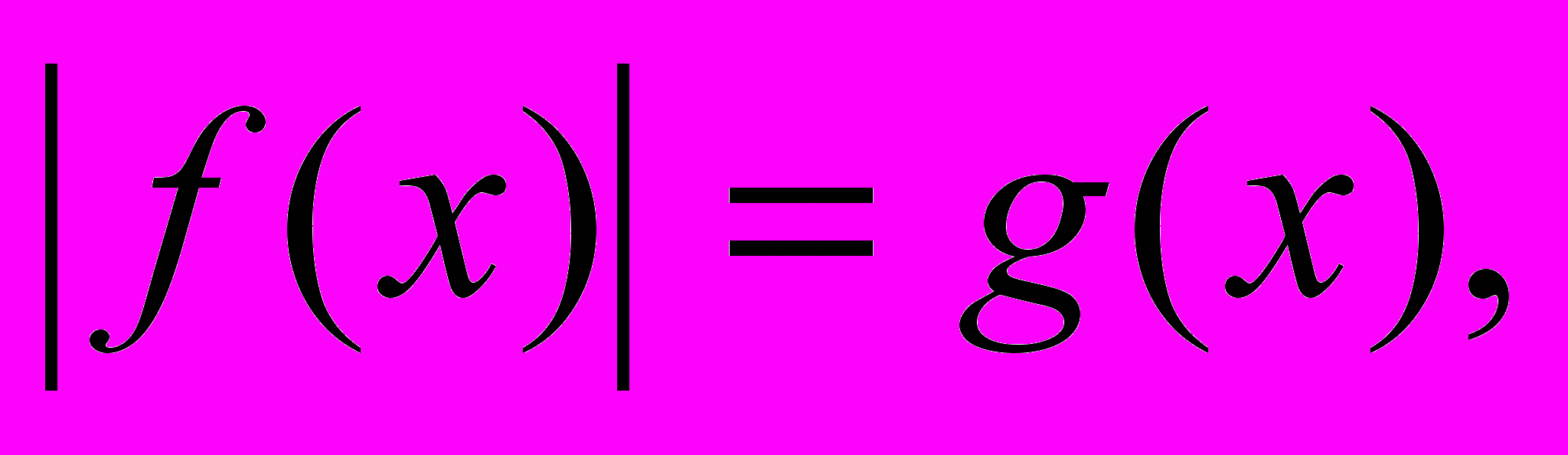
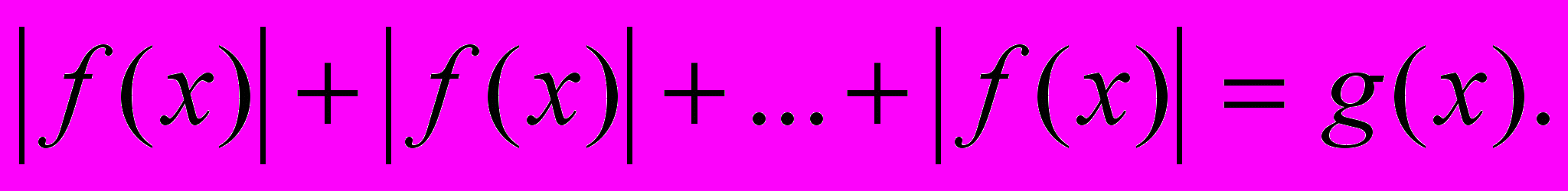
2. Метод равносильного перехода к совокупности двух смешанных систем.
   

Сущность метода. Уравнения вида

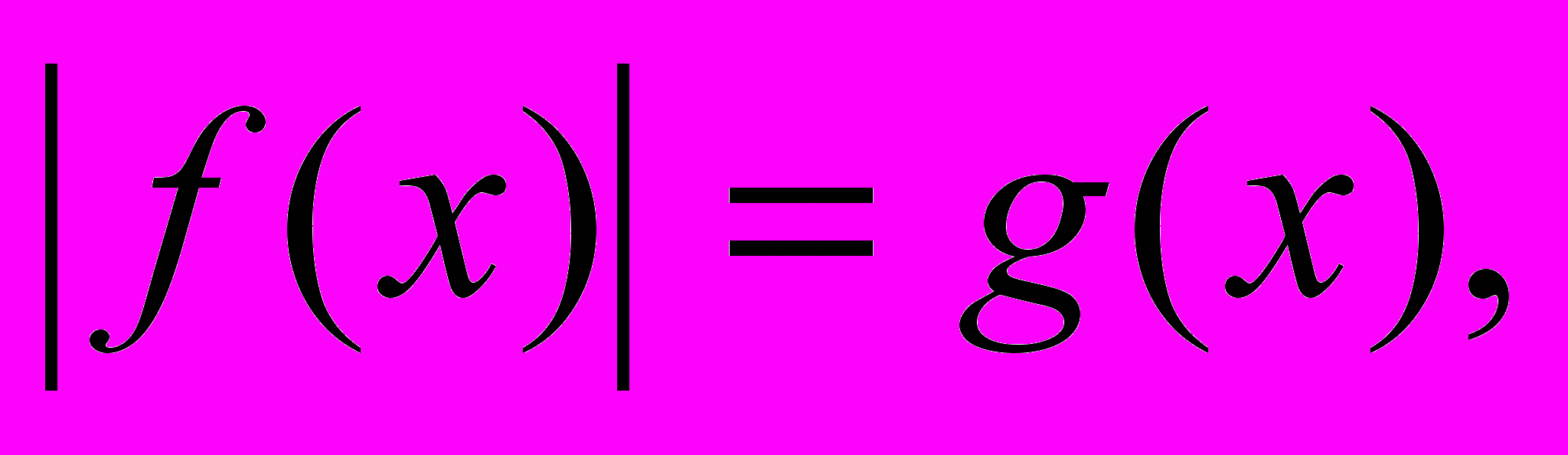
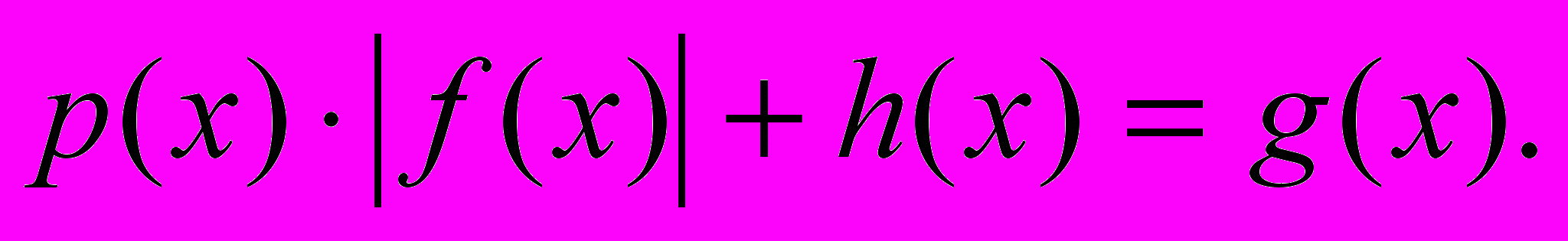
3. Геометрическая интерпретация модуля в задачах.
   

Геометрический смысл модуля действительного числа, графики функций, аналитическое выражение которых содержит знак модуля. Параллельный перенос графиков вдоль осей координат, симметрия относительно осей. Построение графиков функций вида 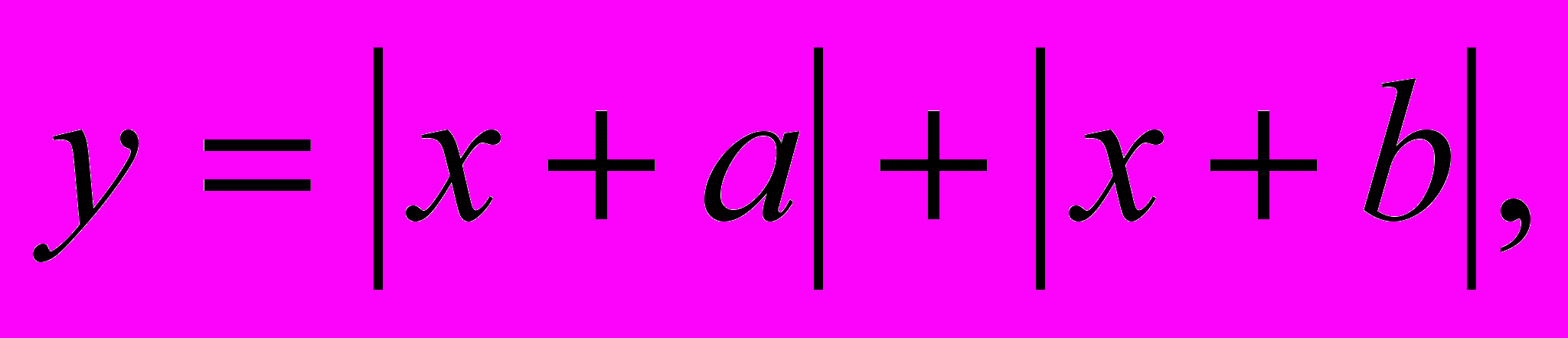где и 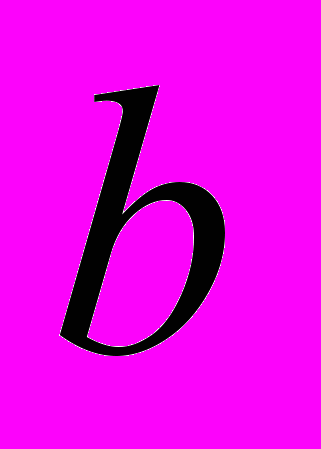- некоторые действительные числа. Преобразование графика функции 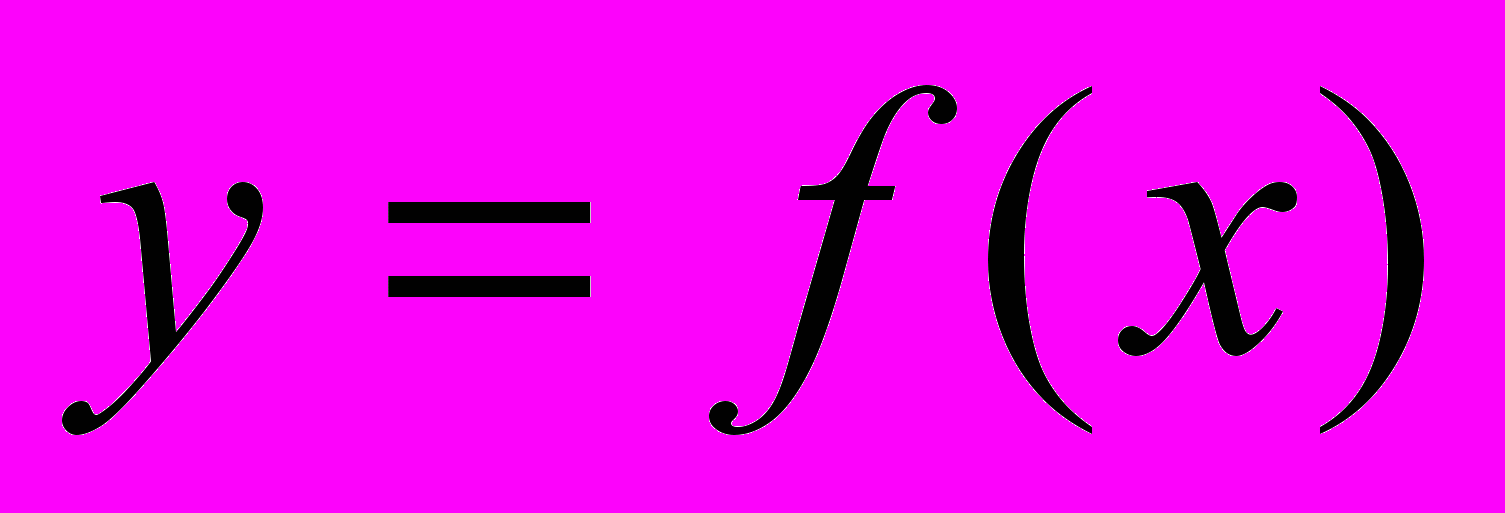в графики функций , , .

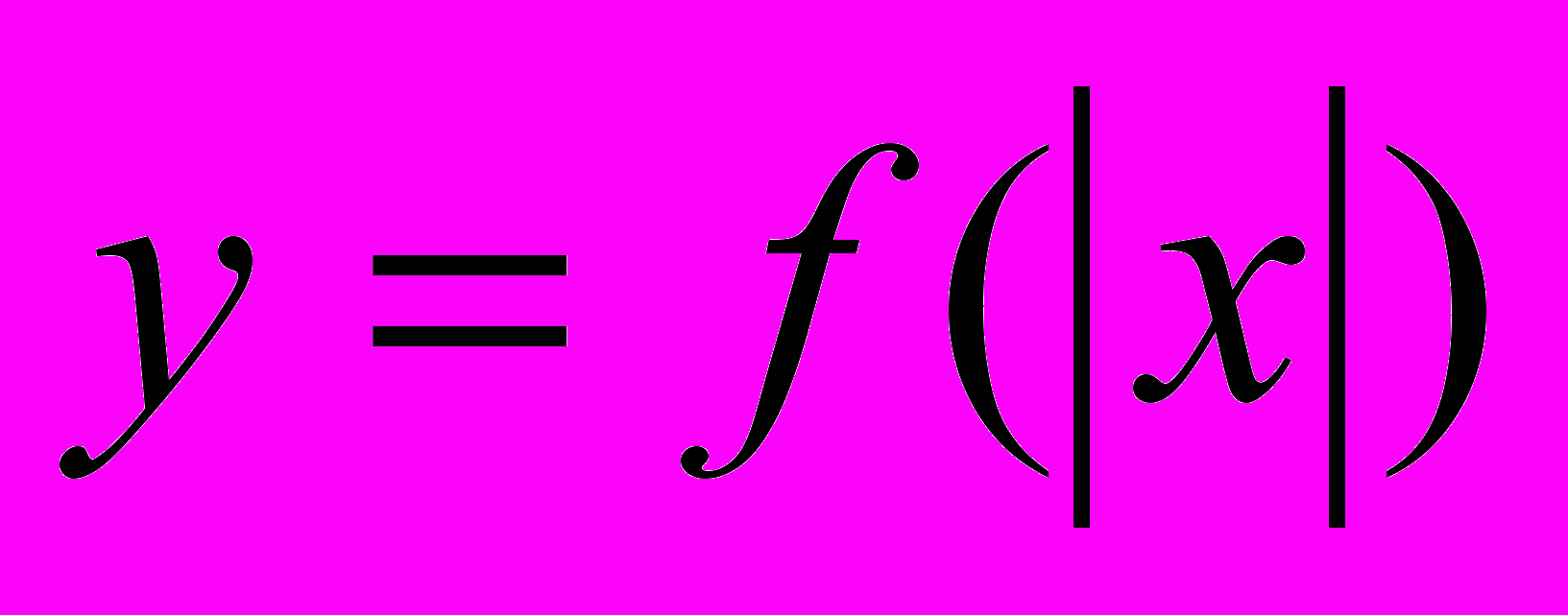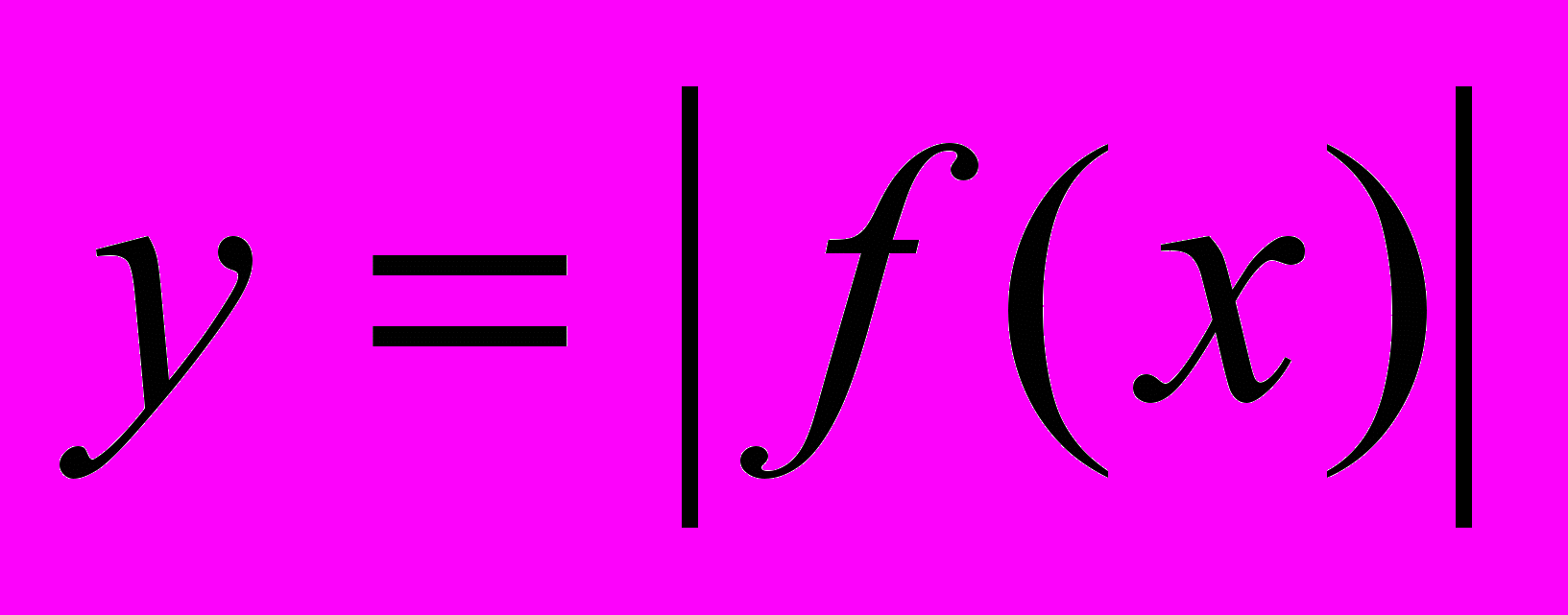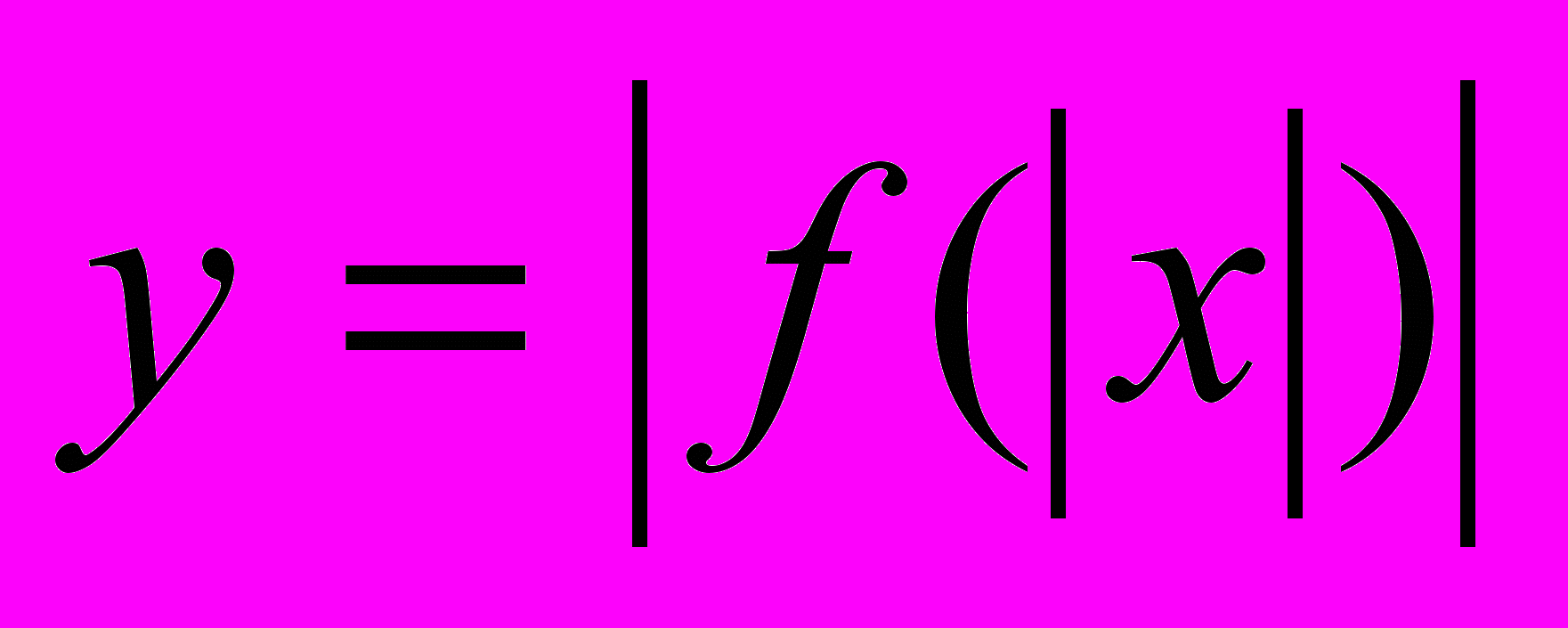3. Логический и графический методы решения уравнений с модулем.
   

Нестандартные решения уравнений, содержащих абсолютные величины. Графический метод решения уравнений с модулями и логический с использованием свойств ограниченности функций.

2. Неравенства, содержащие абсолютные величины.
   

2.1. Метод промежутков.


Сущность метода промежутков. Решение неравенств вида , , , .


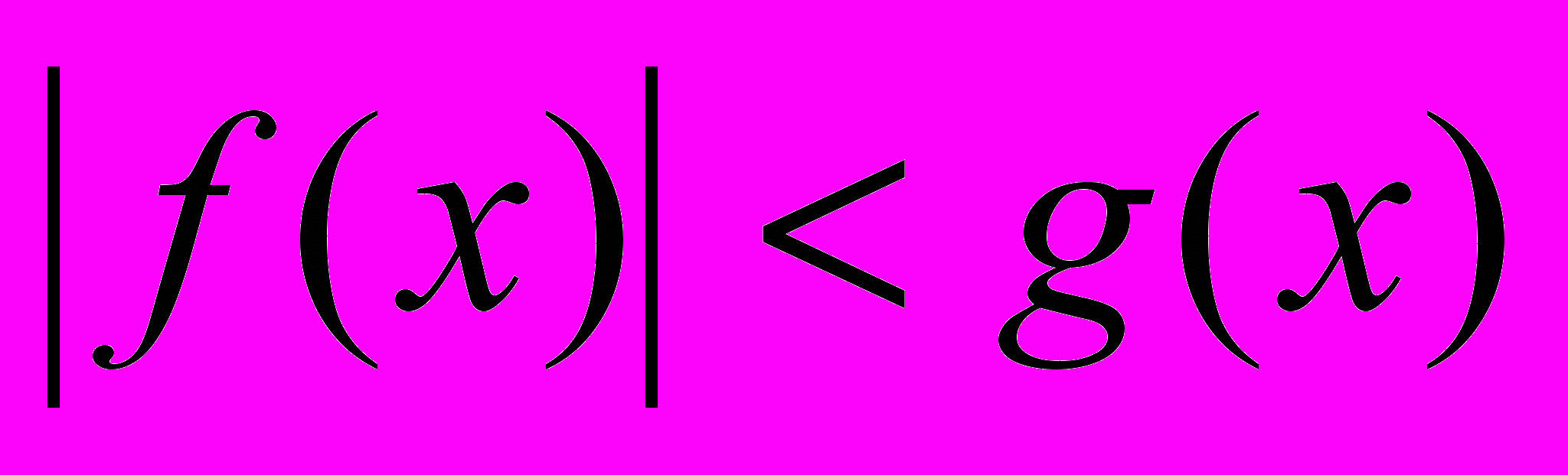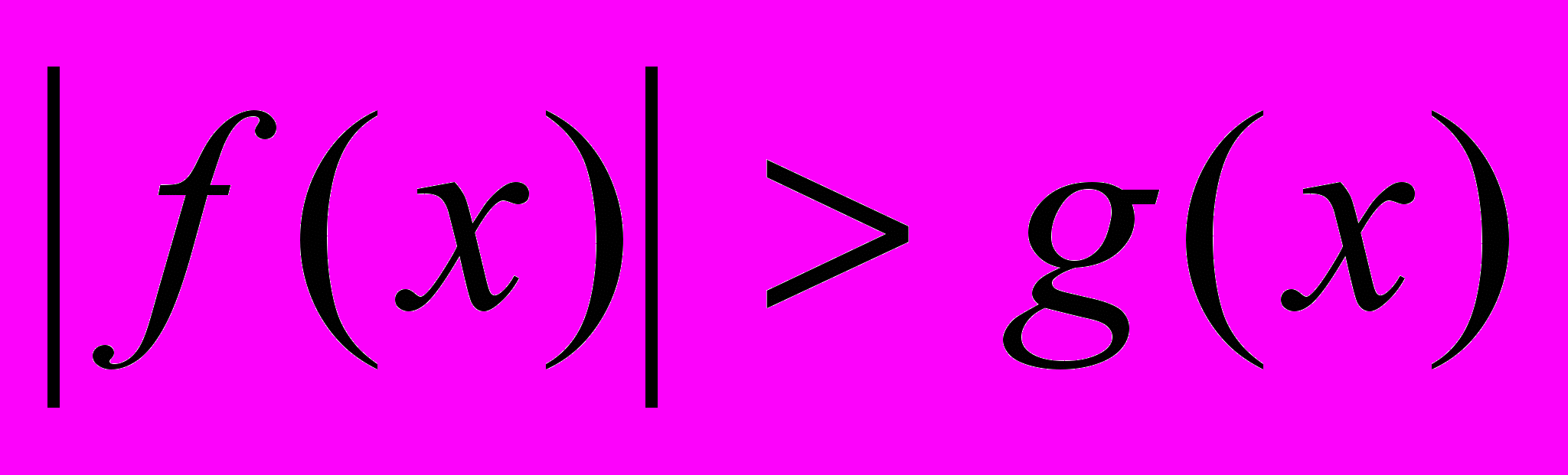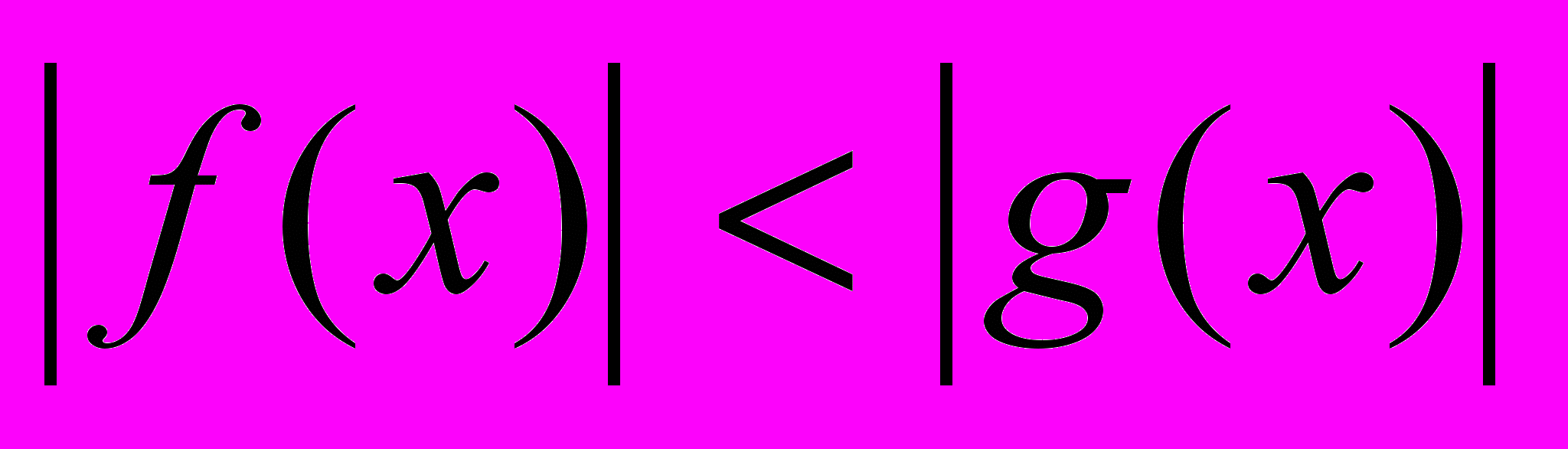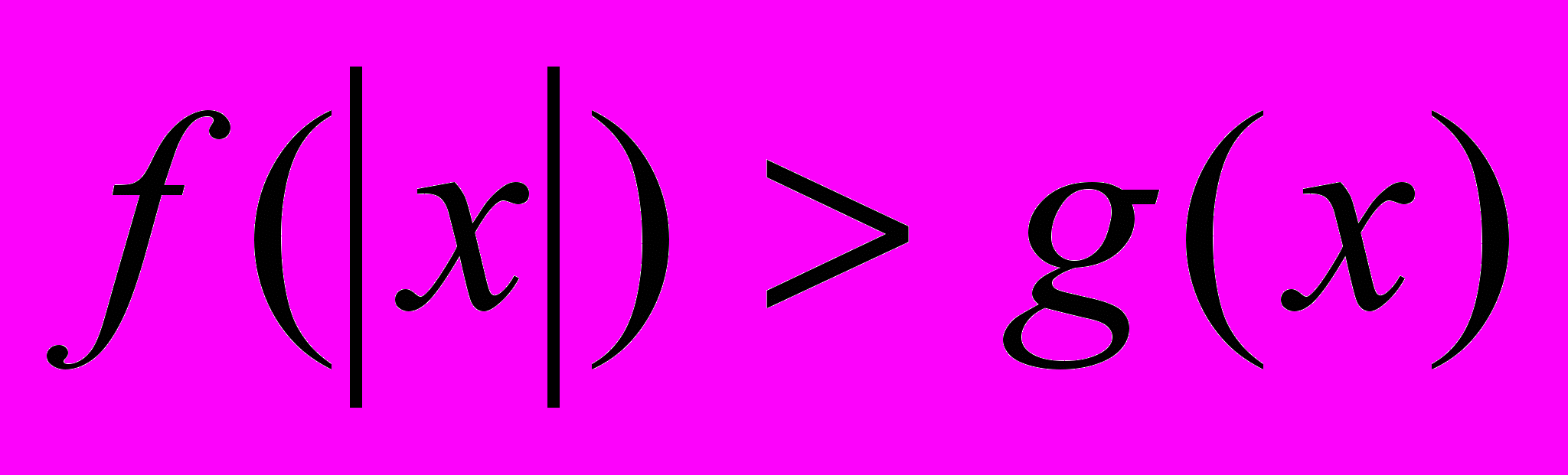2.2. Метод равносильного перехода к совокупности двух систем неравенств.

Сущность метода:

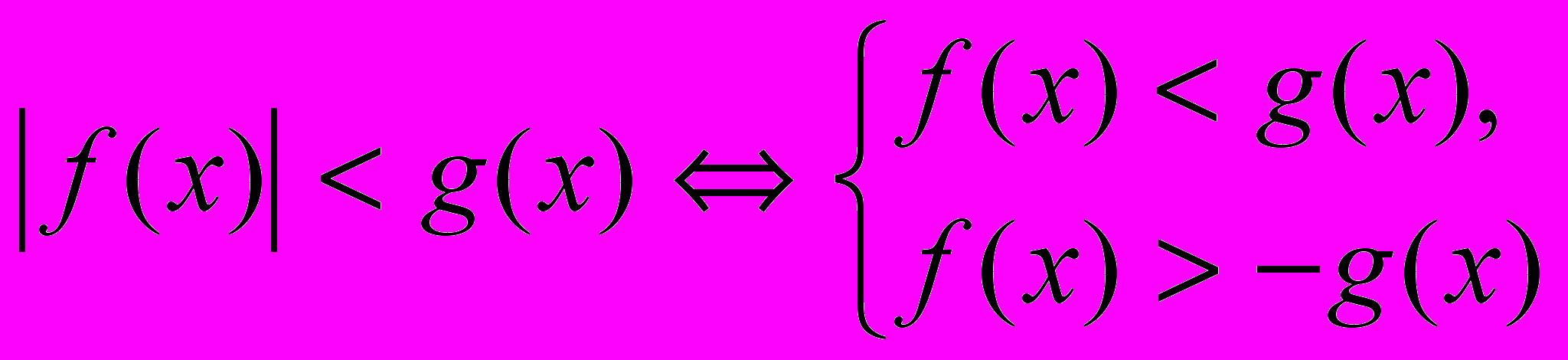
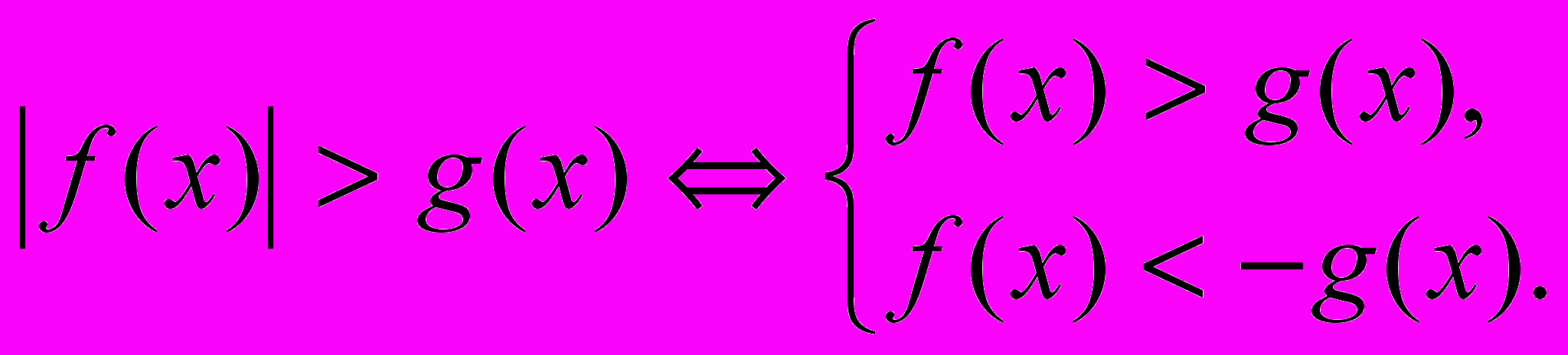
2.3. Логический и графический методы решения неравенств с модулями.

Нестандартные решения неравенств, содержащих абсолютные величины. Графический метод решения неравенств с модулями и логический с использованием свойств ограниченности функций.

2.4. Итоговое тестирование.

Литература

1. Е.Е.Мордовина. Уравнения и неравенства, содержащие абсолютные величины. Тамбов: ТОИПК РО, 2003.
   

2. Матвеева Н.И. Вокруг квадратного трехчлена. Элективный курс предпрофильной подготовки. Тамбов: ТОИПК РО, 2005.
   

3. И.Ф.Шарыгин. Факультативный курс по математике. Решение задач. Учебное пособие для 10 класса средней школы. М.: «Просвещение», 1989.
   

4. Функции и их графики. Учебное пособие. Авт. – сост. Н.В.Бурмистрова, Н.Г.Старостенкова. –Саратов: Лицей, 2003.
   

5. «Математика в школе». Научно-теоретический и методический журнал. №8,2002г. №3,7, 2003 г.
   

6. В.К.Егерев, Б.А.Радунский, Д.А.Тальский. Методика построения графиков функций. М.: «высшая школа», 1970.