Geum.ru

Муравьева Инна Николаевна Р. п. Дмитриевка-2007 программа курса

Вид материалаПрограмма курса

Содержание


I.Организационно-методический раздел.
Тема курса
Подобный материал:
МОУ «Никифоровская средняя общеобразовательная школа №1».


Алгебра матриц


Программа элективного курса для предпрофильной подготовки учащихся 9-го класса по математике.





Составила учитель математики

Муравьева Инна Николаевна


Р.п. Дмитриевка-2007

Программа курса.


Пояснительная записка.


Основная функция курсов по выбору в системе предпрофильной подготовки по математике - выявление средствами предмета математики направленности личности. Её профессиональных интересов. С этой точки зрения курсы, расширяющие базовый курс по математике, дают возможность познакомиться учащимся с интересными, нестандартными вопросами.

Задачи, предлагаемые в данном курсе, увлекательны и часто не просты в решении, что позволяет повысить учебную мотивацию учащихся и проверить свои способности к математике. Вместе с тем, содержание курса позволяет ученику любого уровня активно включиться в учебно-познавательный процесс и максимально проявить себя: занятия могут проводиться на высоком уровне сложности, но включать в себя вопросы, доступные и интересные всем учащимся.


I.Организационно-методический раздел.


Цель курса: познакомить учащихся с матричной символикой и основными понятиями алгебры матриц, а также научить их уверенно оперировать с матрицами как объектами более общего характера по сравнению с числами и функциями, развить прикладной аспект аппарата алгебры матриц.


Место курса в системе предпрофильной подготовки.

Вопросы, рассматриваемые в курсе, выходят за рамки обязательного содержания. Этот курс является базой для изучения последующих спецкурсов по циклу «Прикладная математика». Более того, он полезен уже на первых курсах в институтах при изучении теории линейных электрических цепей, радиоэлектроники, экономики. Работа с матрицами не только экономит время, но и определяет более высокий уровень математической культуры и мышления, поможет оценить свои возможности по математике и более осознанно выбрать профиль дальнейшего обучения.


Требования к уровню освоения содержания курса.


В результате изучения курса «Алгебра матриц» учащиеся узнают:

- основные формы и типы матриц;

- матричную символику;

- особенности матричных операций;

- свойства определителей;

- определение понятий миноров и алгебраических дополнений;

- правило Крамера;

- правило Сарруса;

- алгоритм Жордана-Гаусса.

Умеют:

- складывать, перемножать, транспонировать матрицы;

- вычислять определители;

- решать системы линейных уравнений по правилу Крамера, по алгоритму Жордана-Гаусса, матричным способом.


Занятия целесообразно проводить в форме лекций и практикумов-тренингов с использованием активных методов обучения. Контрольное тестирование по каждой теме позволяет учителю проследить динамику освоения учениками умений и навыков. На изучение элективного курса отводится 34 часа.


Тематическое планирование учебного материала.




№

Тема курса
Количество часов


Всего

Лекция

Практикум

1
Основные понятия.
2






1.1
Введение в предмет



1



1.2
Типы матриц.






1

1.3
Матричная символика.









2.
Операции с матрицами.
10






2.1
Сложение и вычитание матриц.



1
1

2.2
Умножение матриц на скаляр.






1

2.3
Умножение матрицы на матрицу.



1
1

2.4
Свойства действий над матрицами.






1

2.5
Транспонирование матриц.



1
3

3.
Определители.
8






3.1
Понятие определителя. Правило Сарруса.



1
1

3.2
Свойства определителей.






1

3.3
Миноры и алгебраические дополнения.



1
2

3.4
Разложение определителей по Лапласу.






2

4.
Обращение матриц.
5






4.1
Обратная матрица.



1
1

4.2
Вычисление обратной матрицы.



1
2

5.
Методы решения систем линейных уравнений.

9






5.1
Матричный метод- решение уравнений вида АХ=В.



1
1

5.2
Правило Крамера.



1
1

5.3
Алгоритм Жордана-Гаусса.



1
2

5.4
Использование определителей при решении геометрических задач.






1

5.5
Итоговое занятие. Представление «Портфеля достижений».






1




ИТОГО:
34
11
23



II. Содержание курса.


Тема 1. Основные понятия.

Лекция. Введение в предмет. Понятие матриц впервые появилось в середине XIX века в работах У.Гамильтона и А.Кэли. Фундаментальные результаты в теории матриц принадлежат К.Вейерштрассу, К.Жордану, Г.Фробениусу. И.А. Лаппо-Данилевский развил теорию аналитических функций многих матричных переменных и применил её к изучению систем линейных дифференциальных уравнений. Матричная символика оказалась весьма удобным и эффективным способом упорядочивания информации. Представление совокупностей математических объектов (элементов) в виде матриц и разработанные правила операций над ними оказались чрезвычайно плодотворными в математике, и нашли широкое применение в физике, технике, экономике.

Практикум. Рассмотреть различные типы матриц (основная, прямоугольная, квадратная, единичная, диагональная и т.д.), основные преобразования, приводящие к равносильной матрице. Нахождение неизвестного элемента у равной матрицы.


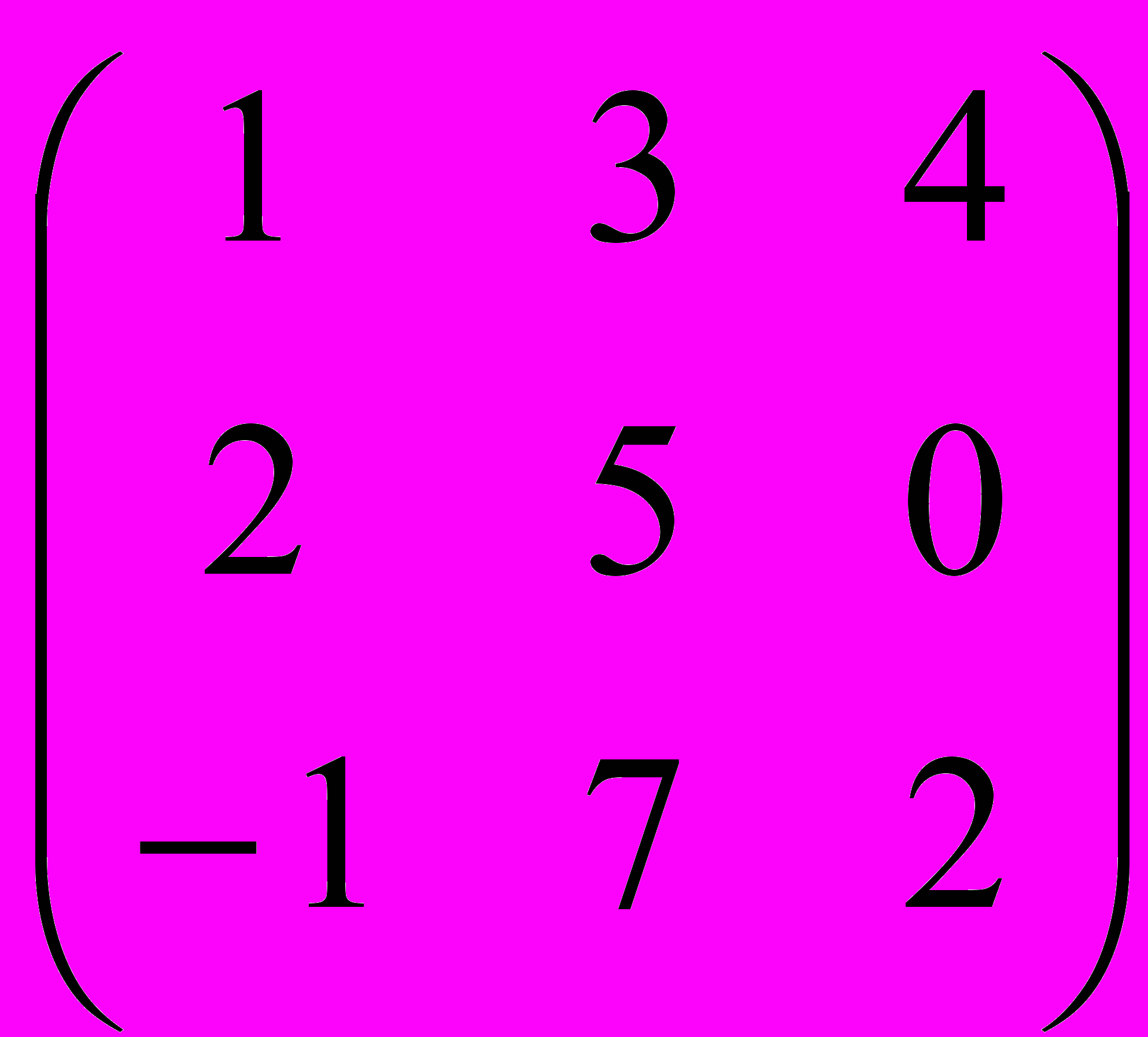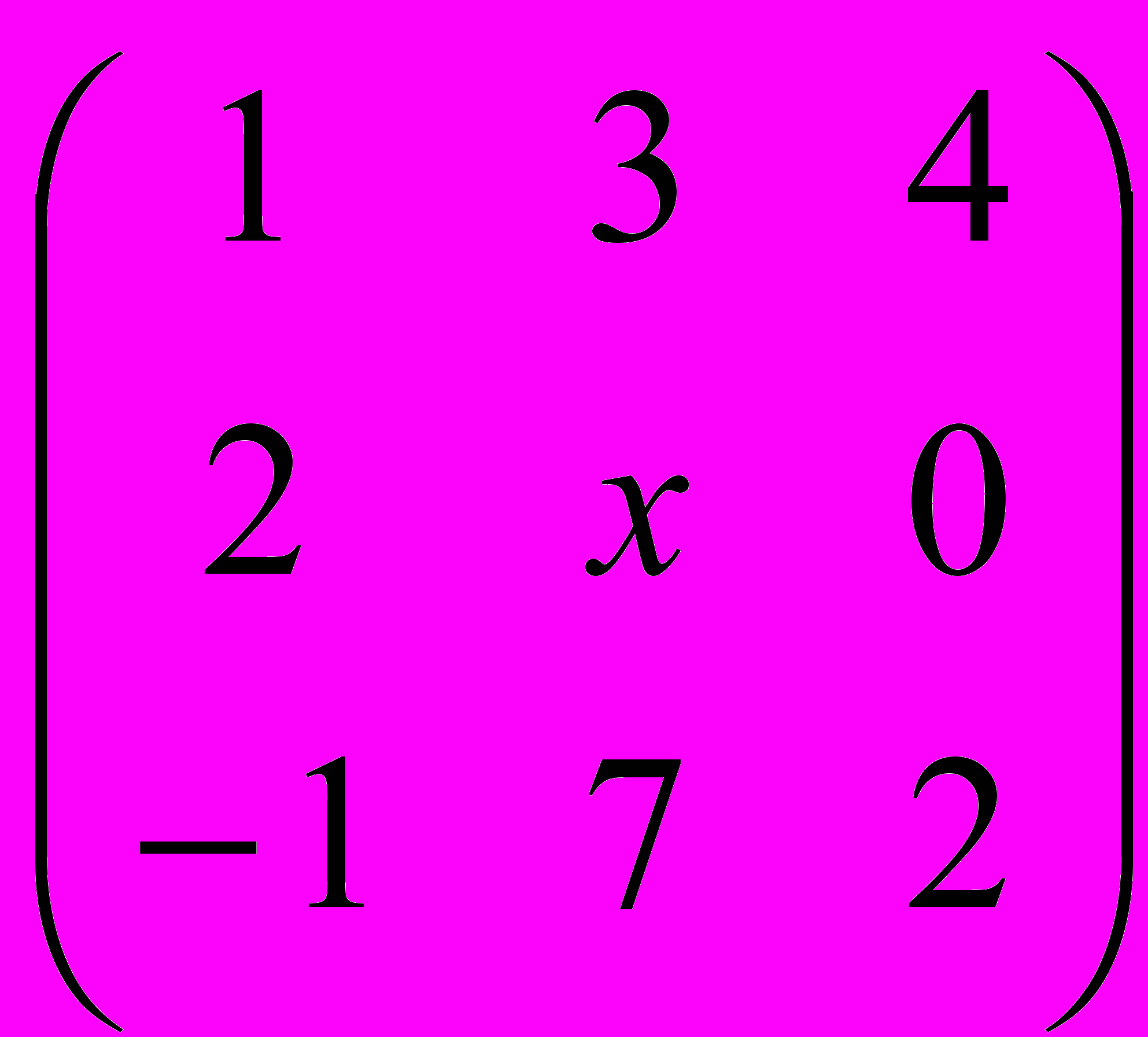
= х=5.


Тема 2. Операции с матрицами.

Лекция. Необходимо рассмотреть действия над матрицами: сложение и вычитание, умножение на число, умножение матриц, транспонирование матриц, перечислить основные свойства операций с матрицами:
  1. А+В=В+А
  2. (А+В)+С=А+(В+С)
  3. А+0=А
  4. А+(-А)=0
  5. 1×А=А
  6. α×(β×А)=(α×β)×А
  7. α(А+В)=α×А+ α×В
  8. (α+β) А= α×А+ β×В
  9. А×В≠В×А
  10. (А+С)×В=АВ+СВ
  11. (АВ) С=А (ВС)
  12. (αА)™=αА™
  13. (А+В)™=А™+В™
  14. (А В)™=В™×А™


Тема 3. Определители.

Ввести понятия определителей, миноров и алгебраических дополнений. Научить детей разлагать определители по Лапласу и правилу Сарруса.


Тема 4. Обращение матриц.

На практических занятиях научить вычислять обратные матрицы по правилу:
  1. Найти определитель матрицы, убедиться, что он не равен 0.
  2. Найти все алгебраические дополнения элементов матрицы, записать новую матрицу.
  3. Транспонировать её.
  4. Умножить каждый элемент на 1/Д.



Тема 5.Методы решения систем линейных уравнений.

Показать практическое направление использование матриц: решение систем линейных уравнений матричным способом, по правилу Крамера, использование определителей при решении геометрических задач.

Итоговое занятие можно провести в Форме презентации своего «Портфеля достижений».


III.Учебно-методическое обеспечение курса.


Литература.

  1. Блох Э.Л., Лошинский Л.И., Турин В.Я. Основы линейной алгебры.-М..1971.
  2. Гантмахег Ф.Р. Теория матриц. - М., 1966.
  3. Хедли Д. Линейная алгебра. - М.,1966.
  4. Головина Л.И. Линейная алгебра и некоторые её приложения. – М., 1975.
  5. Сборник задач по математике для поступающих в ВУЗы. Под ред. А.И. Прилепко. – М.: Высшая школа, 1989.
  6. Сборник задач по математике для поступающих во ВТУЗы. Под ред. М.И. Сканави. – М.: Просвещение, 2004.