Тема «Иррациональные уравнения и неравенства» введение
| Вид материала | Документы |
- Тема: «Рациональные и иррациональные уравнения, неравенства и системы», 199.57kb.
- Элективный курс по математике для учащихся 9 класса тема: «уравнения и неравенства,, 248.15kb.
- Поурочное планирование (5 часов в неделю, всего 170 часов) Тема, 155.46kb.
- Урок математики с информатикой по теме «Иррациональные уравнения и неравенства», 43.05kb.
- Программа элективного курса Показательные, логарифмические, иррациональные уравнения, 113.96kb.
- Программа Элективного курса по математике «Иррациональные уравнения и неравенства», 227.79kb.
- Элективный курс квадратичная зависимость и связанные с ней уравнения, неравенства, 45.88kb.
- Тема: Введение, 237.37kb.
- П. В. Чулков, «Уравнения и неравенства в школьном курсе математики, лекции 1-4», стр, 8.44kb.
- Урок по алгебре и началам математического анализа «Иррациональные уравнения», 96kb.
Тема «Иррациональные уравнения и неравенства»
ВВЕДЕНИЕ
В школьном курсе алгебры рассматриваются различные виды уравнений – линейные, квадратные, биквадратные, кубические, рациональные, с параметрами, иррациональные и другие. Данный раздел посвящен иррациональным уравнениям, методам их решения. Кроме того, в разделе введены понятия уравнений следствий и равносильных уравнений, а также приведены примеры задач, математическими моделями которых служат иррациональные уравнения. Приведенася небольшая историческая справка, посвященная введению иррациональных чисел
^1. ИЗ ИСТОРИИ
Термин «рациональное» (число) происходит от латиноамериканского слова ratio – отношение, которое является переводом греческого слова “логос”в отличие от рациональных чисел, числа, выражающие отношение несоизмеримых величин, были названы еще в древности иррациональными, т.е. нерациональными (по-гречески “алогос”) правда, первоначально термины “рациональный” и “иррациональный” относились не к числам, а к соизмеримым и соответственно не соизмеримым величинам, которые пифагорейцы называли выразимыми и невыразимыми, Теодор Киренский же симметричными и ассимметричными. В V-VI вв. римские авторы Капелла и Кассиодор переводили эти термины на латынь словами rationalis и irrationalis. Термин «соизмеримый» (commensurabilis) ввел в первой половине VI в. другой римский автор- Боэций.
Древнегреческие математики классической эпохи пользовались только рациональными числами (вернее целыми, дробными и положительными). В своих «Началах» Евклид излагает учение об иррациональностях чисто геометрически.
Математики Индии, Ближнего и Среднего Востока, развивая алгебру, тригонометрию и астрономию, не могли обойтись без иррациональных величин, которые, однако, длительное время не признавали за числа. Греки называли иррациональную величину, например, корень из квадратного числа, «алогос» – невыразимое словами, а позже европейские переводчики с арабского на латынь перевели это слово латинским словом surdus – глухой. В Европе термин surdus- глухой впервые появился в середине XII в. у Герарда Кремонского, известного переводчика математических прозведений с арабского на латынь, затем у итальянского математика Леонардо Фабоначчи и других европейских математиков, вплоть до XVIII в. Правда уже в XVI в. Отдельные ученые, в первую очередь итальянский математик Рафаэль Бомбелли и нидерландский математик Симон Стевин считали понятие иррационального числа равноправным с понятием рационального числа. Стевин писал: «Мы приходим к выводу, что не существует никаких абсурдных, иррациональных, неправильных, необъяснимых или глухих чисел, но что среди чисел существует такое совершенство и согласие, что нам надо размышлять дни и ночи над их удивительной закономерностью.»
Еще до Бомбелли и Стевина многие ученые стран Среднего Востока в своих трудах употребляли иррациональные числа как полноправные объекты алгебры. Более того, комментируя «Начала» Евклида и исследуя общую теорию отношения Евдокса, Омар Хайям уже в начале XII в. теоретически расширяет понятие числа до положительного действительного числа. В том же направлении много было сделано крупнейшим математиком XIII в. ат-Туси.
Математики и астрономы Ближнего и Среднего Востока вслед за астрономами древнего Вавилона и эллинистической эпохи широко пользовались шестидесятеричными дробями, арифметические действия с которыми они называли «арифметикой астрономов». По аналогии с шестидесятеричными дробями самаркандский ученый XV в. ал-Каши в работе «Ключ арифметики» ввел десятичные дроби которыми он пользовался для повышения точности извлечения корней. Независимо от него по такому же пути шел открывший в 1585 г. десятичные дроби в Европе Симон Стевин, который в своих «приложениях к алгебре» (1594 г.) показал, что десятичные дроби можно использовать для бесконечно близкого приближения к действительному числу. Таким образом, уже в XVI в. зародилась идея о том, что естественным аппаратом для введения и обоснования понятия иррационального числа являются десятичные дроби. Появление «Геометрии» Декарта облегчило понимание связи между измерением любых отрезков (и геометрических величин вообще) и необходимости расширения понятия рационального числа. На числовой оси иррациональные числа, как и рациональные, изображаются точками. Это геометрическое толкование позволило лучше понять природу иррациональных чисел и способствовало их признанию.
В современных учебных руководствах основа определения иррационального числа опирается на идеи ал-Каши, Стевина и Декарта об измерении отрезков и о неограниченном приближении к искомому числу с помощью бесконечных десятичных дробей. Однако обоснованием свойств действительных чисел и полная теория их была разработана лишь в XIX в.
^ 2. ОПРЕДЕЛЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ
- Равносильные уравнения. Следствия уравнений.
При решении уравнений выполняются различные тождественные преобразования над выражениями, входящими в уравнение. При этом исходное уравнение изменяется другими, имеющими те же корни. Такие уравнения называются равносильными.
Определение: Уравнение f(x)=g(x) равносильно уравнению f1(x)=g1(x), если каждый корень первого уравнения является корнем второго и обратно, каждый корень второго уравнения является корнем первого, т.е. их решения совпадают.
Например, уравнения 3x-6=0; 2х–1=3 равносильны, т.к. каждое из уравнений имеет один корень х=2.
Любые два уравнения, имеющие пустое множество корней, считают равносильными.
 Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны, обозначают так:
Тот факт, что уравнения f(x)=g(x) и f1(x)=g1(x) равносильны, обозначают так:f

(x)=g(x) f1(x)=g1(x)
В процессе решения уравнений важно знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.
Теорема 1: ^ Если какое-либо слагаемое перенести из одной части уравнения в другую, изменив его знак, то получим уравнение, равносильное данному.
Доказательство:
Докажем, что уравнение f(x) = g(x)+q(x) (1)
равносильно уравнению
f(x) – q(x) = g(x) (2)
Пусть х=а – корень уравнения. Значит имеет место числовое равенство f(a)=g(a)+q(a) . Но тогда по свойству действительных чисел будет выполняться и числовое равенство f(a)-q(a)=g(a) показывающее, что а – корень уравнения (2). Аналогично доказывается, что каждый корень уравнения (2) является и корнем уравнения (1).
Что и требовалось доказатью.
Теорема 2: ^ Если обе части уравнения умножить или разделить на отличное от нуля число, то получим уравнение, равносильное данному.
Доказательство: докажем, что уравнение 6х–3=0 равносильно уравнению ^ 2х–1=0
решим уравнение 6х–3=0 и уравнение 2х–1=0
6х=3 2х=1
х=0,5 х=0,5
так как корни уравнений равны, то уравнения равносильны.
Что и требовалось доказать.
Рассмотрим уравнение
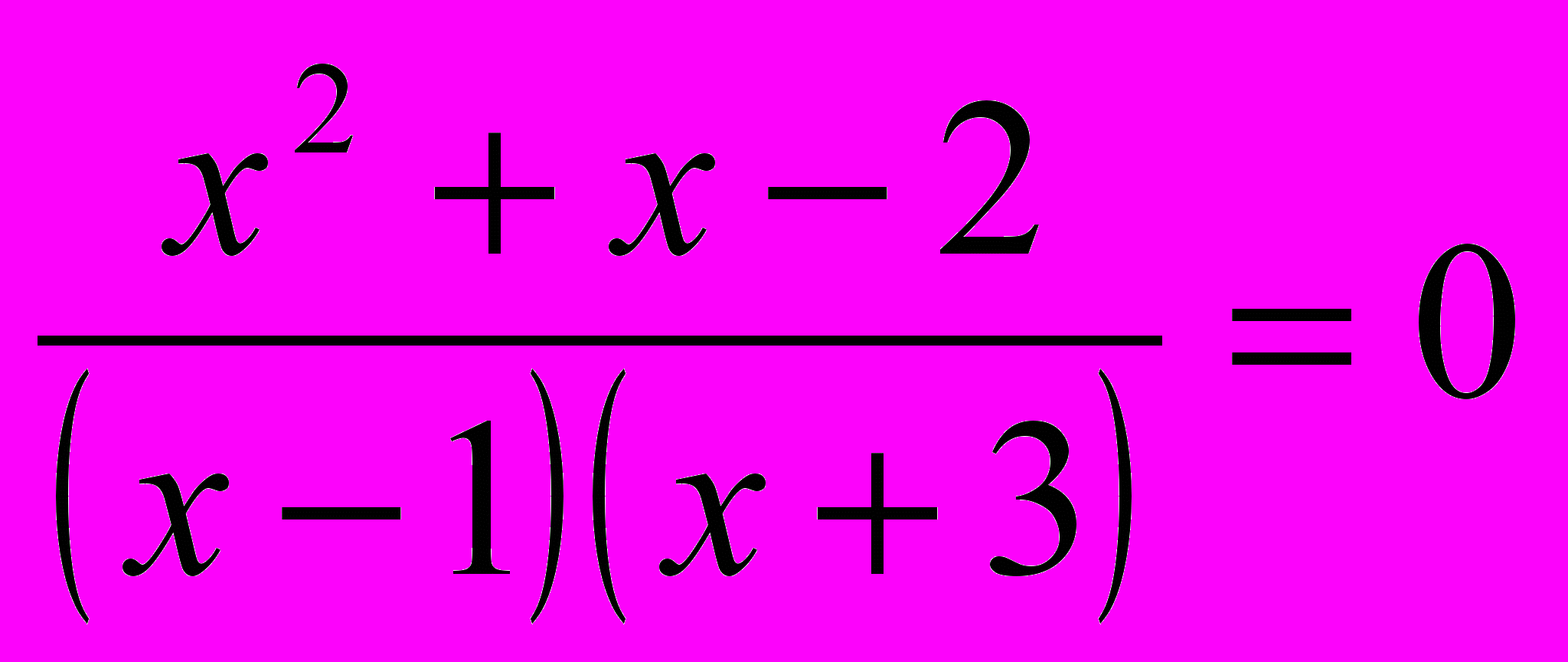
ОДЗ этого уравнения {х ≠ 1, х ≠ -3}
Мы знаем, что дробь равна нулю в том случае, когда ее числитель равен нулю, т.е. х²+х–2=0, а знаменатель не равен 0. Решая уравнение х²+х–2=0, находим корни х1=1, х2 = –2 . Но число 1 не входит в ОДЗ данного уравнения и значит, исходное уравнение имеет один корень х=-2.
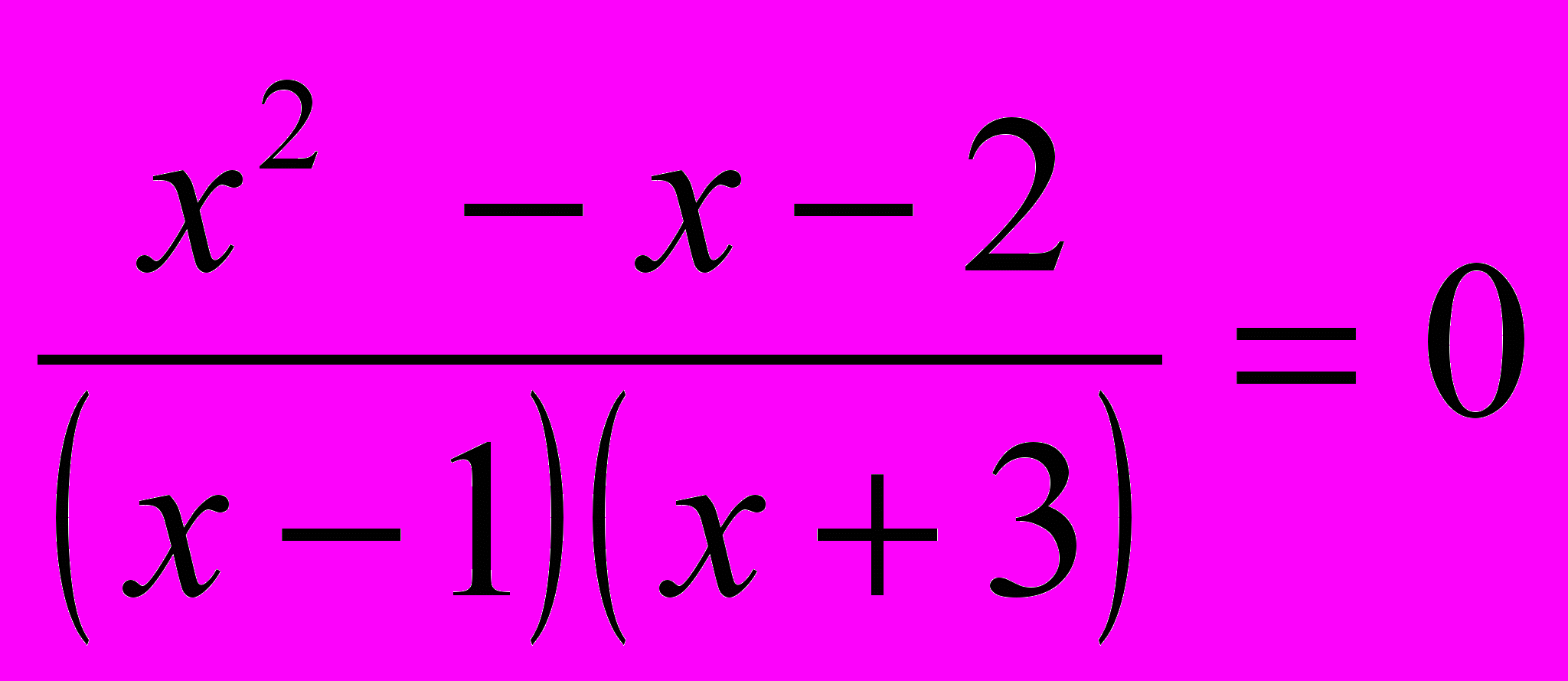
В этом случае говорят, что уравнение х²+х–2=0, есть следствие уравнения
пусть даны два уравнения:
f1 (x) = g1 (x) (3)
f2 (x) = g2 (x) (4)
Если каждый корень уравнения (3) является корнем уравнения (4), то уравнение (4) называют следствием уравнения (3).
Э

тот факт записывают так:
В том случае, когда уравнение (3) - есть также следствие уравнения (4), эти уравнения равносильны.
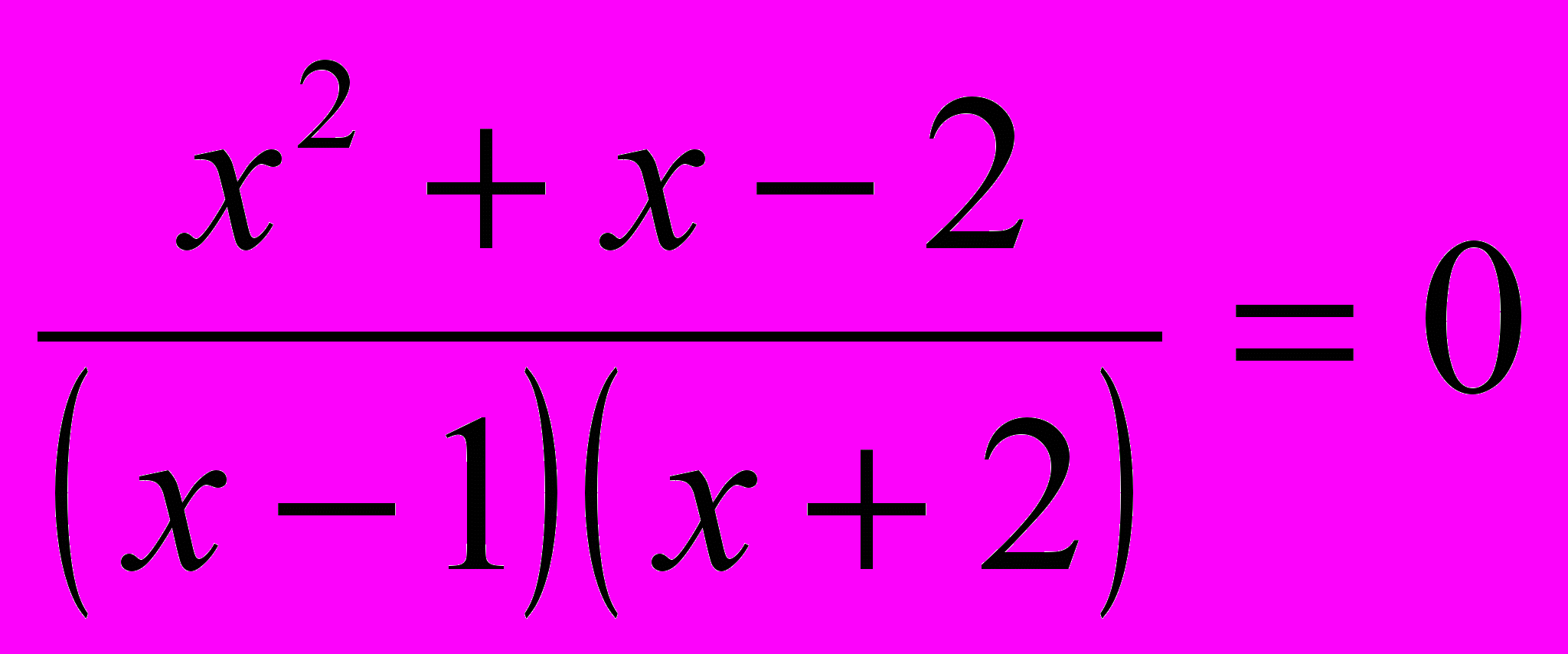
^ Два уравнения равносильны в том, и только в том случае, когда каждое из них является следствием другого.
В приведенном выше примере уравнение – следствие
х²+х–2=0, имеет два корня x1=1 и х2 =-2, а исходное уравнение имеет один корень х=-2. В этом случае корень х=1 называют посторонним для исходного уравнения

В общем случае корни уравнения-следствия, не являющиеся корнями исходного уравнения, называют посторонними.

Итак, если при решении уравнения происходит переход к уравнению – следствию, то могли появиться посторонние корни. В этом случае все корни уравнения-следствия нужно проверить, подставляя их в исходное уравнение. В некоторых случаях выявление посторонних корней облегчается знанием ОДЗ исходного уравнения – корни, не принадлежащие ОДЗ, можно сразу отбросить. Так, в приведенном примере посторонний корень х=1 не входит в ОДЗ уравнения
и потому отброшен.
И

ногда посторонние корни могут появиться и при тождественных преобразованиях, если они приводят к изменению ОДЗ уравнения. Например, после приведения подобных членов в левой части уравнения
ОДЗ которого {х -2},

п

олучим уравнение следствие х²-4=0 имеющее два корня х1 = 2, х2 = -2 корень х2 = -2 – посторонний, так как не входит в ОДЗ исходного уравнения.
В тех случаях, когда в результате преобразований произошел переход от исходного уравнения к уравнению, не являющемуся его следствием, возможна потеря корней.
Например, уравнение (х+1)(х+3)= х+1 (5)
Имеет два корня. Действительно, перенося все члены уравнения в левую часть и вынося х+1 за скобки, получим (х+1)(х+2)=0, откуда находим х1=-1, х2=-2 .
Если же обе части уравнения (5) разделить («сократить») на х+1, то получим уравнение х+3=1, имеющее один корень х=-2. В результате такого преобразования корень х=-1 потерян. Поэтому делить обе части уравнения на выражение, содержащее переменную, можно лишь в том случае, когда это выражение отлично от нуля.
Для того, чтобы в процессе решения уравнения избежать потери корней, необходимо следить за тем, чтобы переход осуществлялся либо к равносильным уравнениям, либо к уравнениям-следствиям.
2.2. Определение иррациональных уравнений.
Иррациональными называются уравнения, в которых переменная содержится под знаком корня или под знаком операции возведения в дробную степень.
Например:
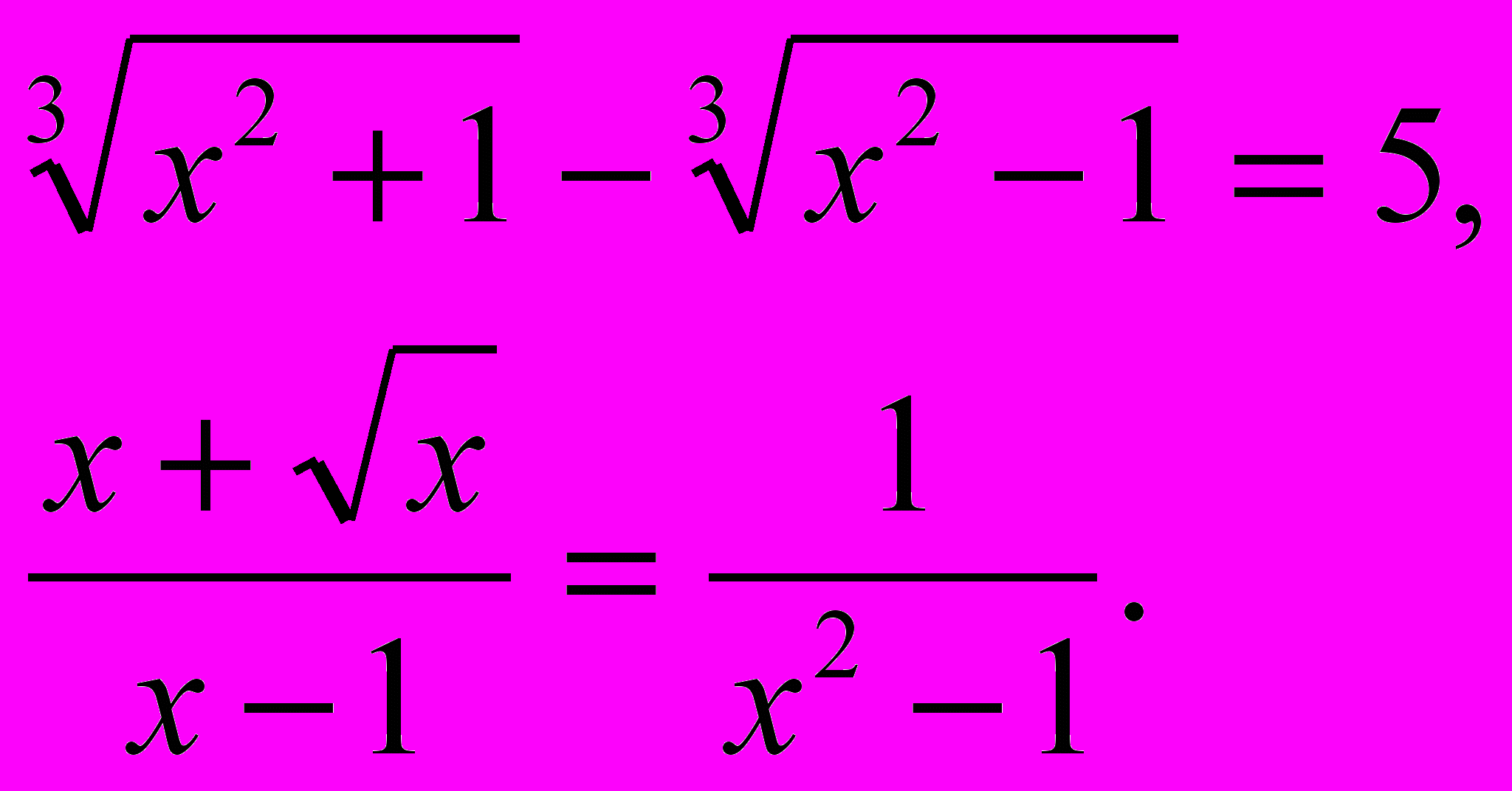
^ 3. МЕТОДЫ РЕШЕНИЯ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ.
3.1. Решение иррациональных уравнений методом возведения обеих частей уравнения в одну и ту же степень.
^
Пример №1
Р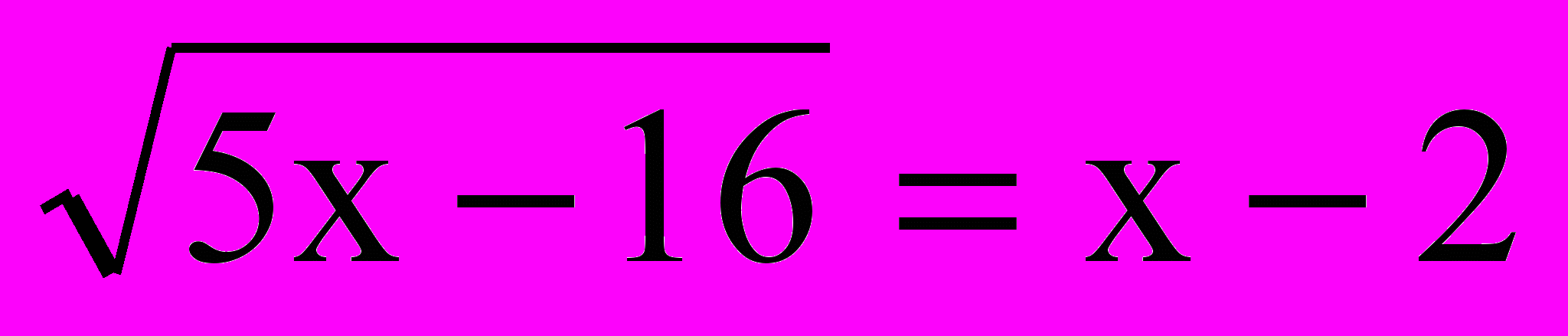
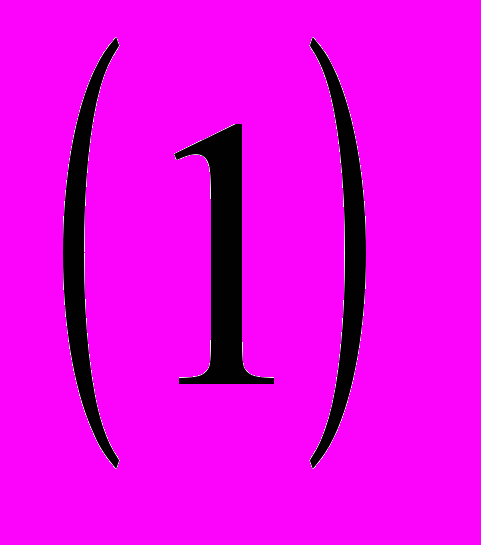
ешить уравнение
В
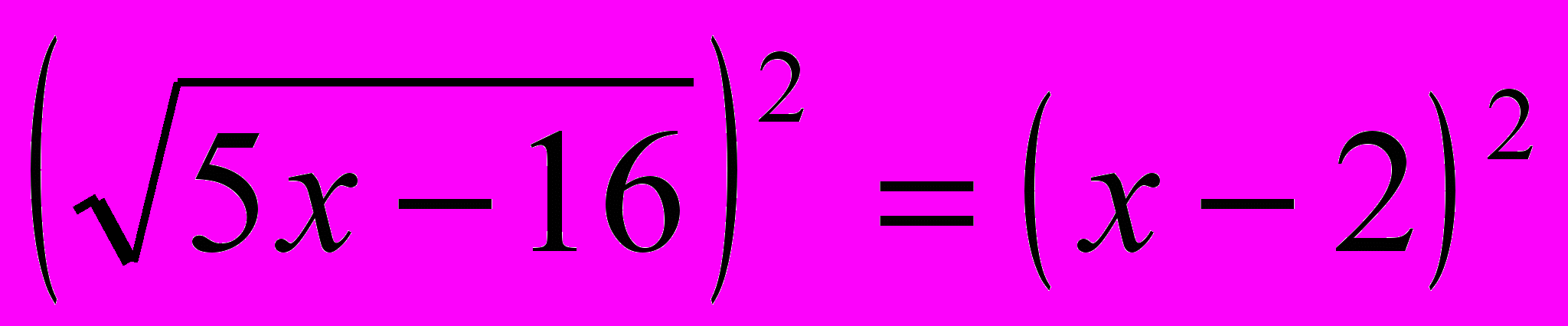
озведем обе части уравнения (1) в квадрат:
далее последовательно имеем:
5х – 16 = х² - 4х + 4
х² - 4х + 4 – 5х + 16 = 0
х² - 9х + 20 = 0
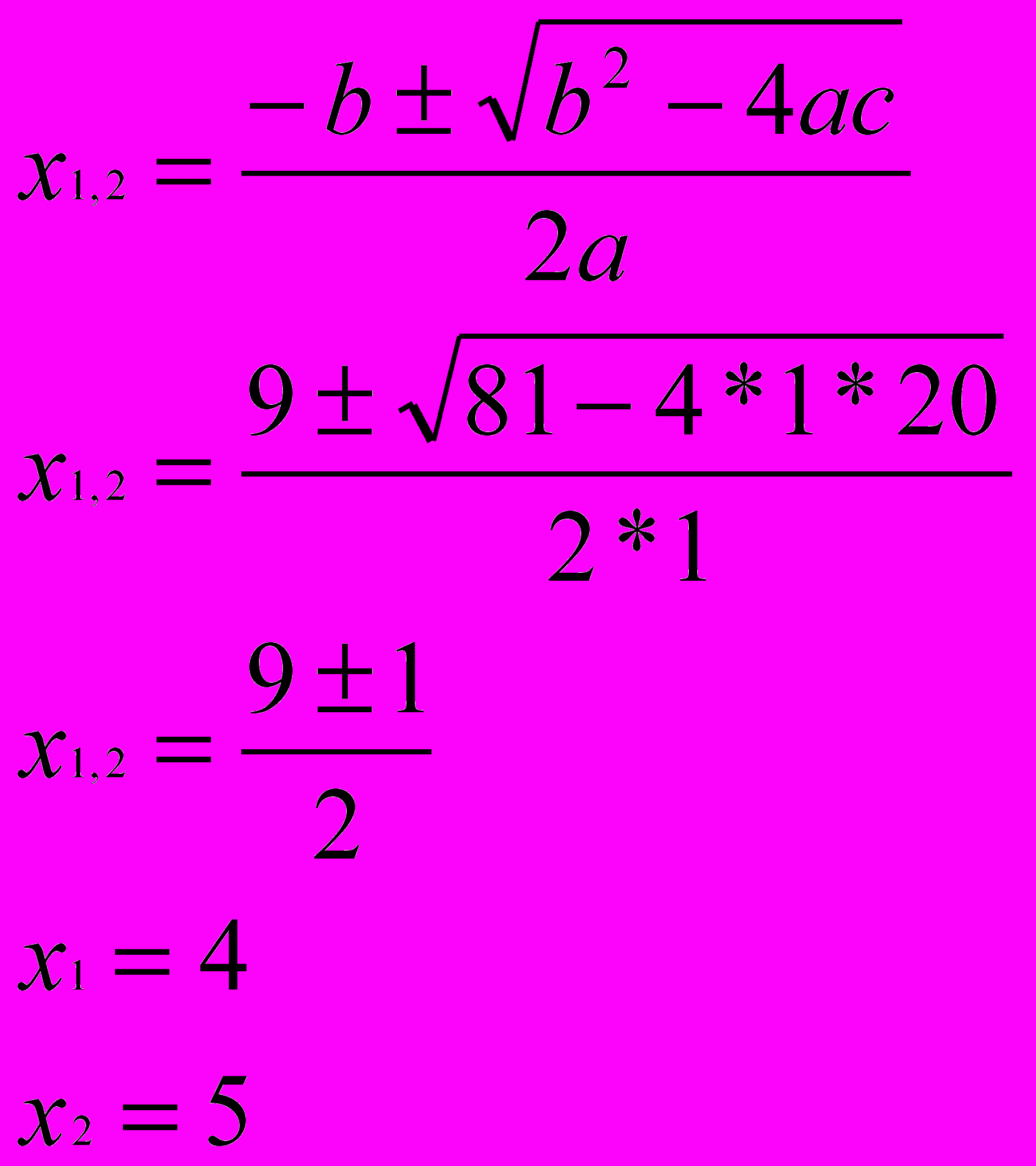
П
 роверка: Подставив х=5 в уравнение (1), получим – верное равенство. Подставив х= 4 в уравнение (1), получим – верное равенство. Значит оба найденных
роверка: Подставив х=5 в уравнение (1), получим – верное равенство. Подставив х= 4 в уравнение (1), получим – верное равенство. Значит оба найденных значения – корни уравнения.
Ответ: 4; 5.
Пример №2
Решить уравнение:
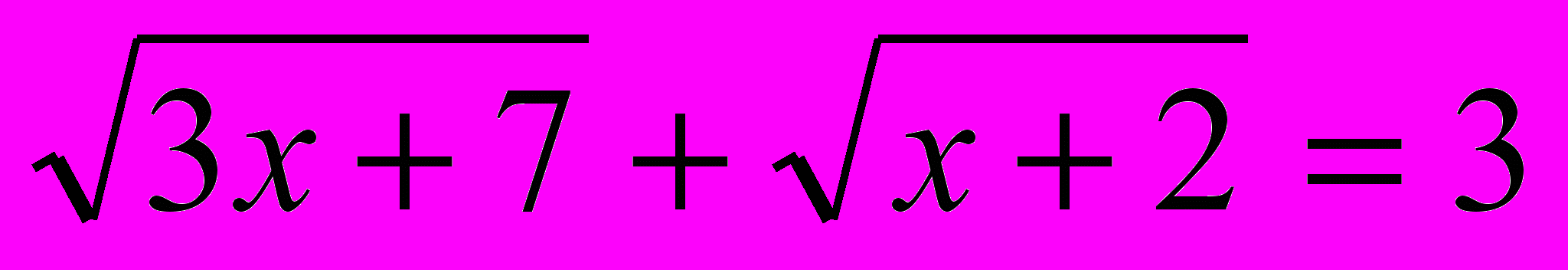
(2)
Решение:
Преобразуем уравнение к виду:
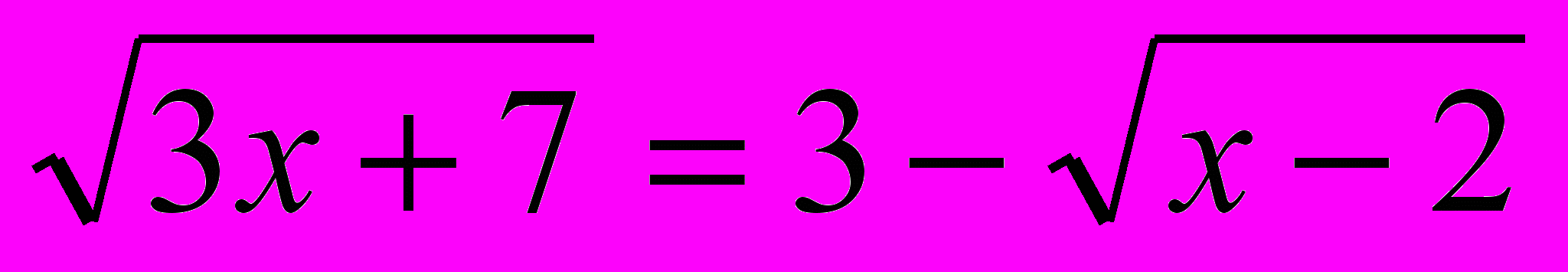 и применим метод возведения в квадрат:
и применим метод возведения в квадрат:
далее последовательно получаем.
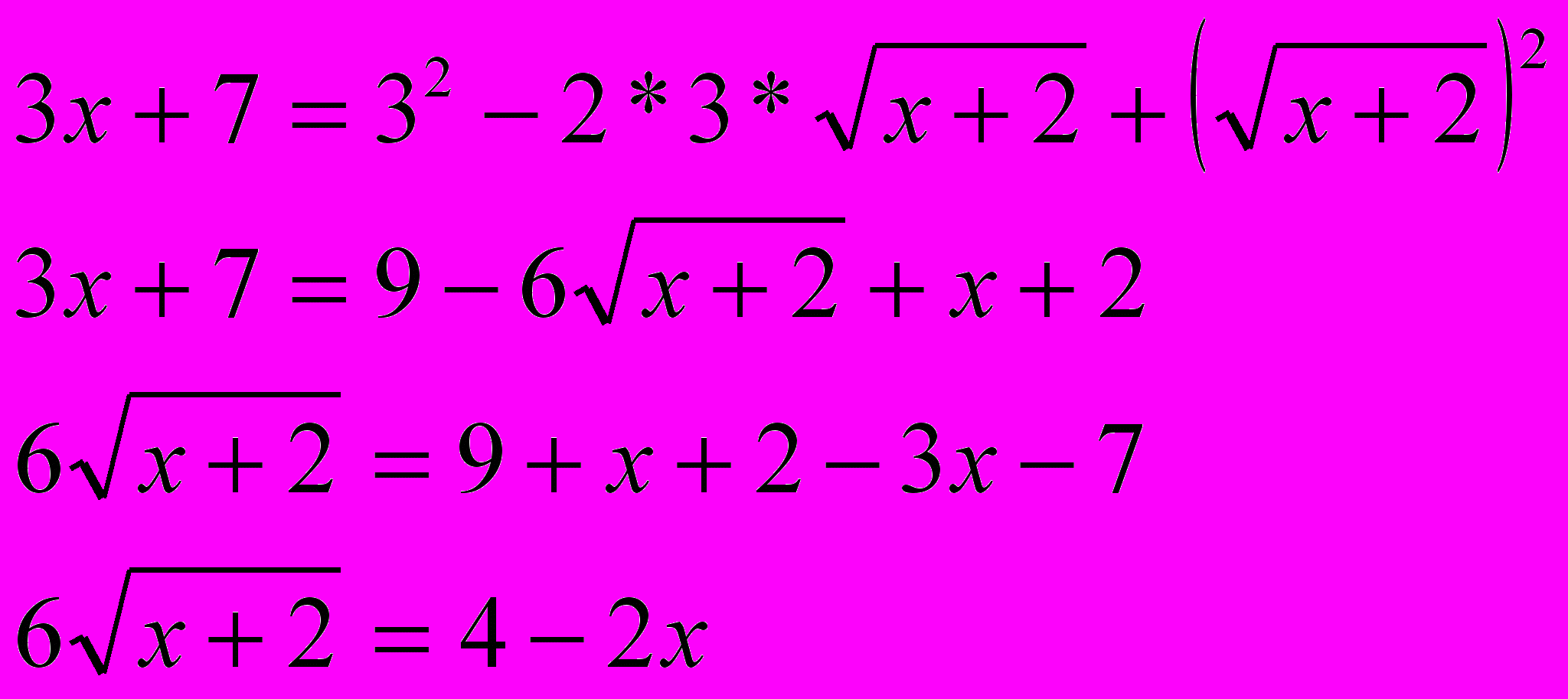
Р
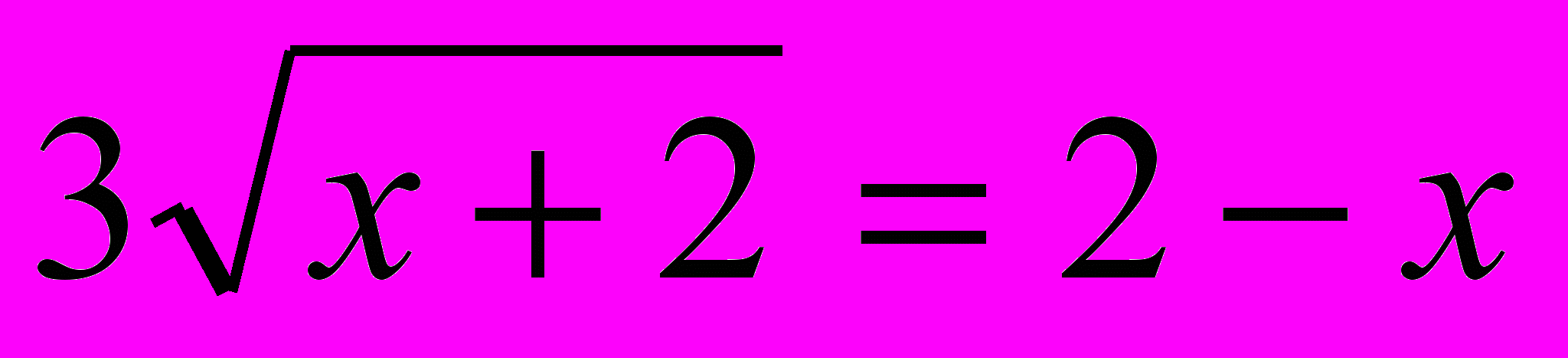
азделим обе части последнего уравнения почленно на 2:
е

ще раз применим метод возведения в квадрат:
далее находим:
9(х+2)=4–4х+х²
9х+18–4+4х-х²=0
-х²+13х+14=0
х²-13х–14=0
х1+х2 =13 х1 =19
х1 х2 = -14 х2 = -1
по теореме, обратной теореме Виета, х1=14, х2 = -1
корни уравнения х²-13х–14 =0
Проверка: подставив значение х=-14 в уравнение (2), получим–
- не верное равенство. Поэтому х = -14 – не корень уравнения (2).
^
 Подставив значение x=-1 в уравнение (2), получим-
Подставив значение x=-1 в уравнение (2), получим-
- верное равенство. Поэтому x=-1- корень уравнения (2).
Ответ: -1
3.2 Метод введения новых переменных.
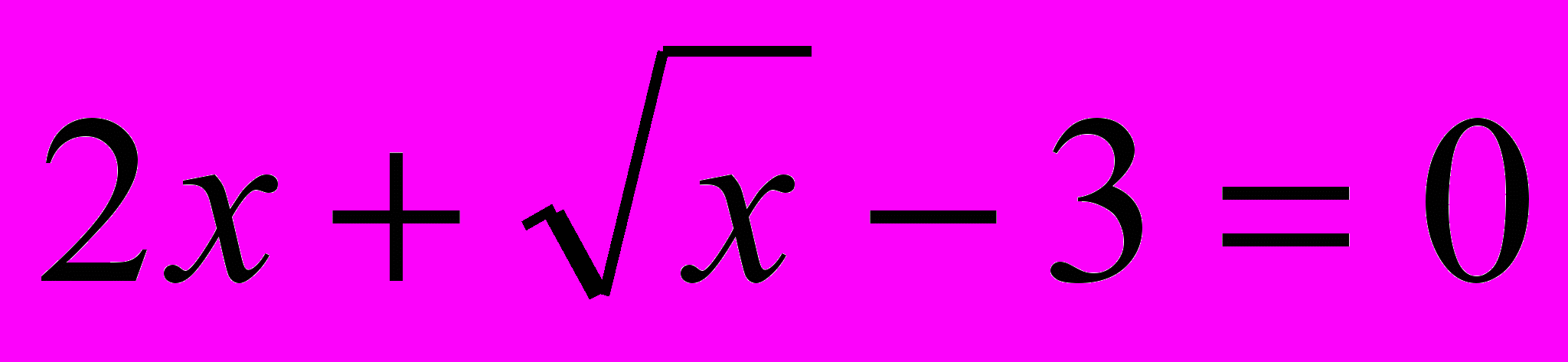
^
Решить уравнение
Решение:
Конечно, можно решить это уравнение методом возведения обеих частей уравнения в одну и ту же степень. Но можно решить и другим способом – методом введения новых переменных.
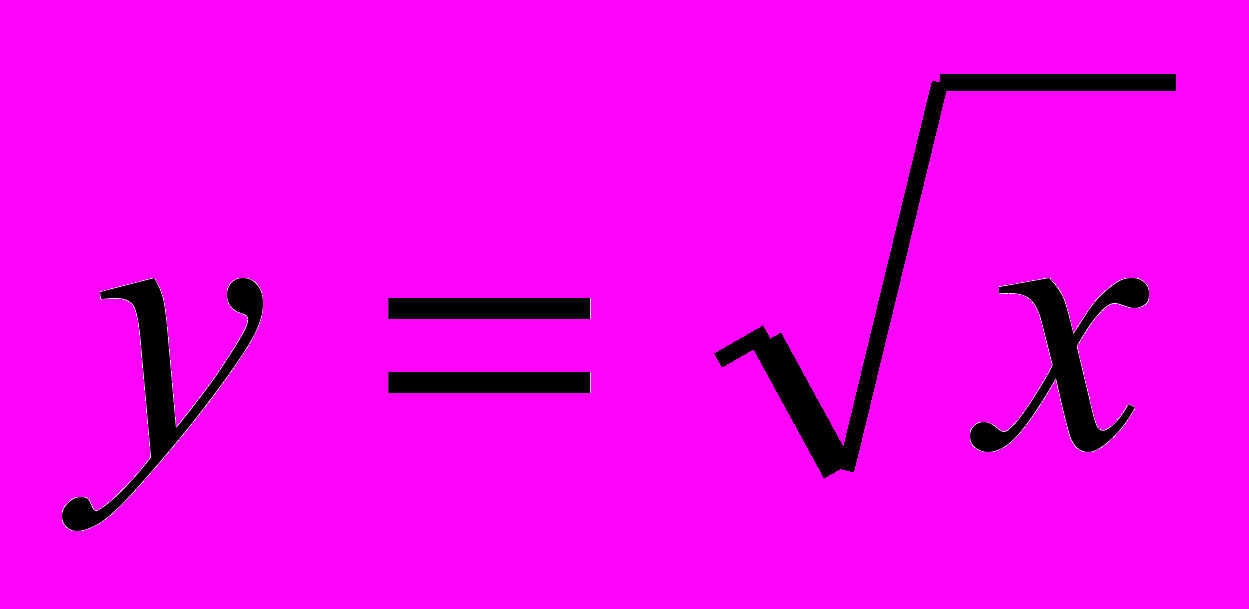
Введем новую переменную Тогда получим 2y²+y–3=0 – квадратное уравнение относительно переменной y. Найдем его корни:
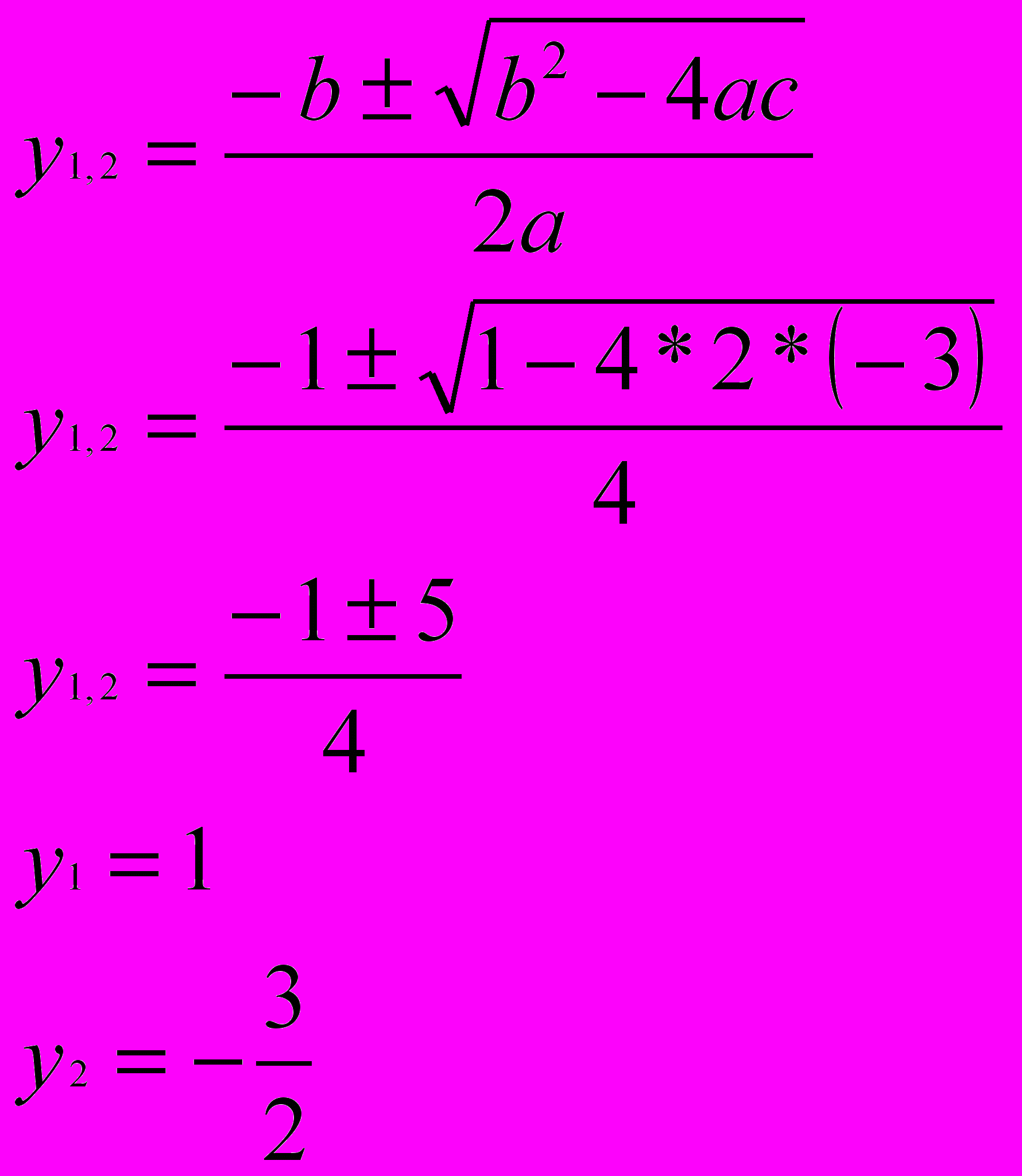
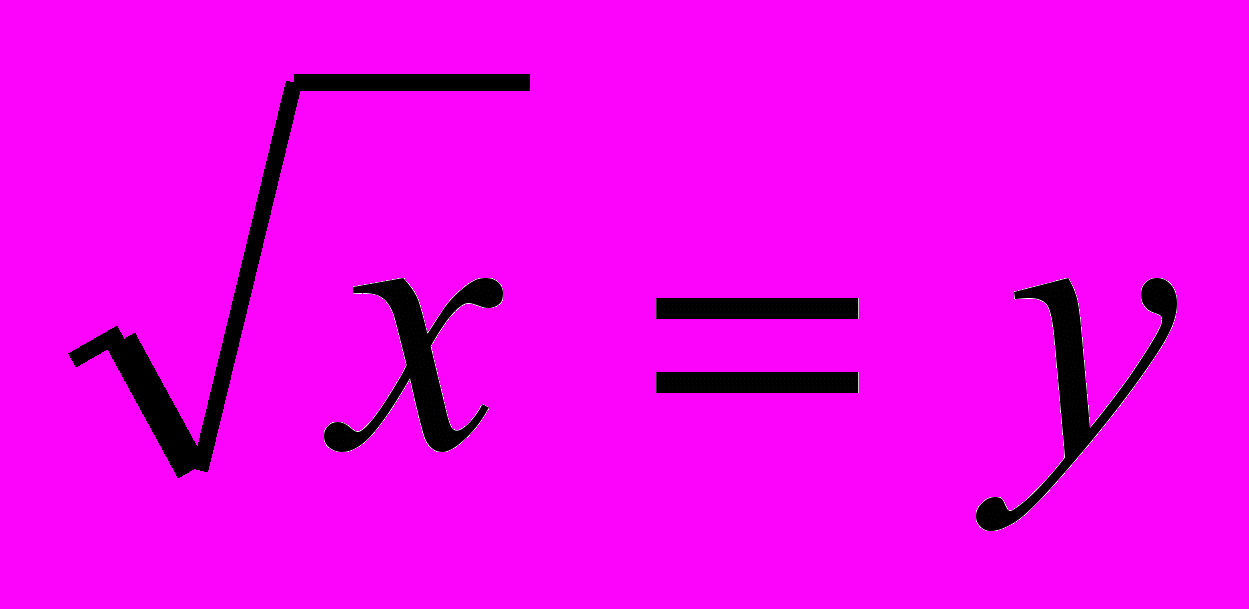
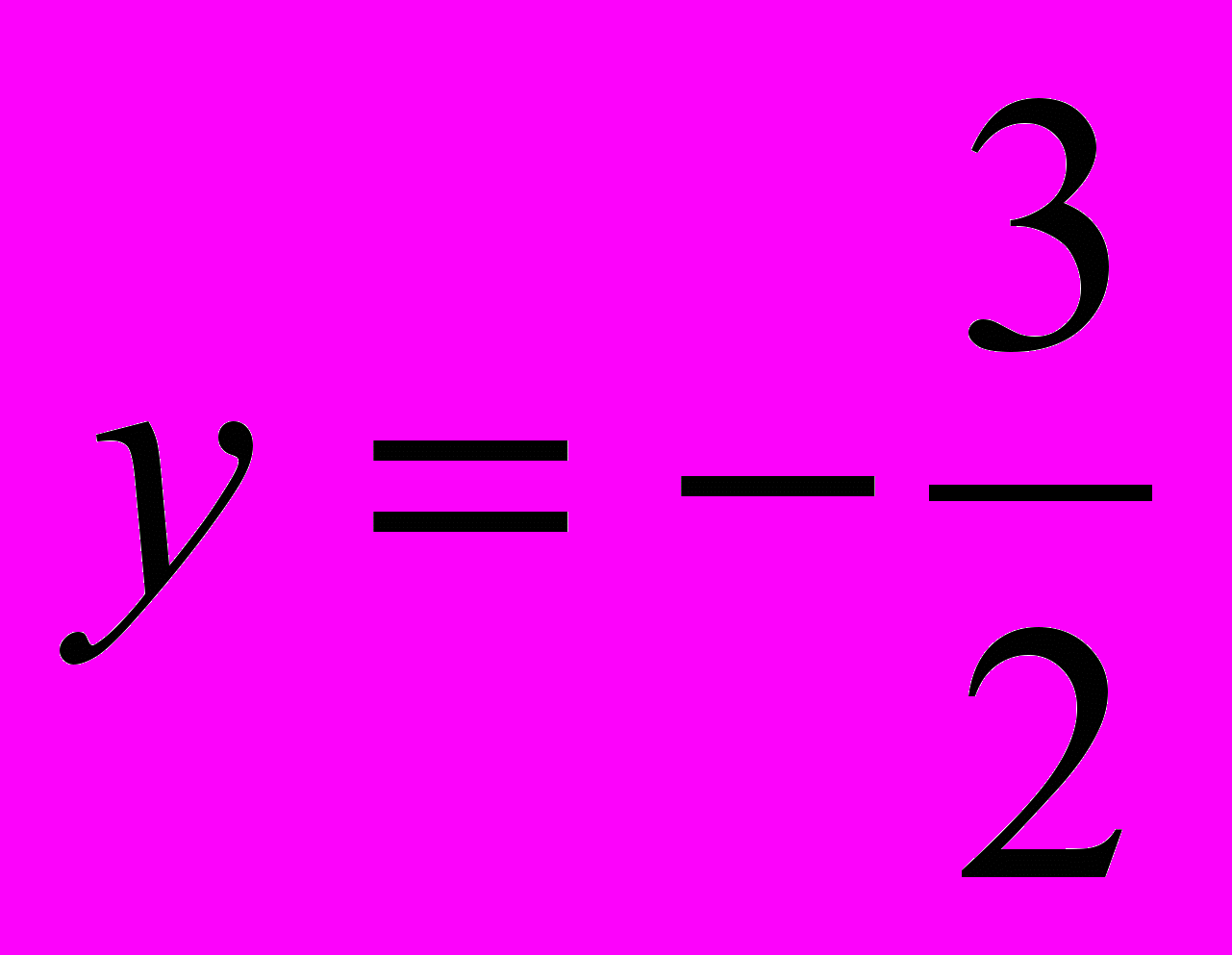
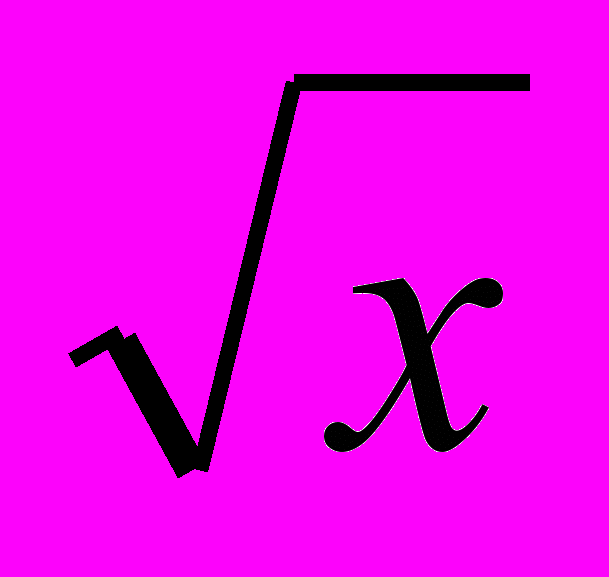
Т.к. , то – не корень уравнения, т.к. не
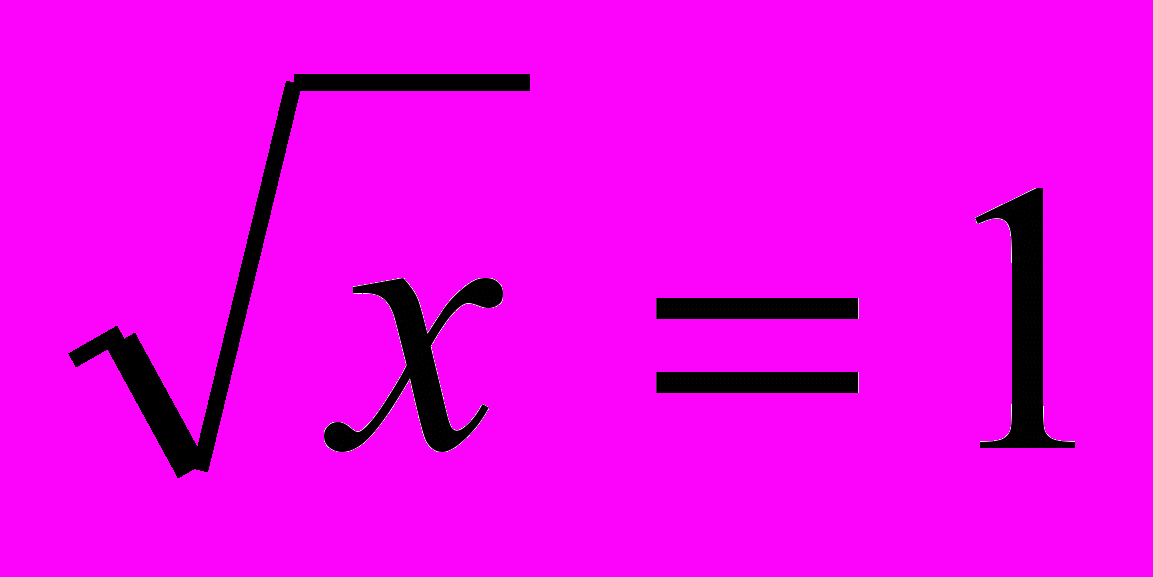
может быть отрицательным числом . А - верное равенство, значит x=1- корень уравнения.
Ответ: 1.
- Искусственные приёмы решения иррациональных уравнений.
Решить уравнение:
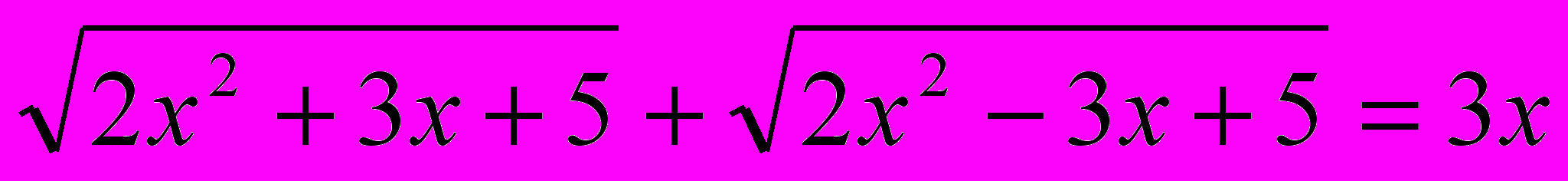
(1)
Решение:
^
Умножим обе части заданного уравнения на выражение
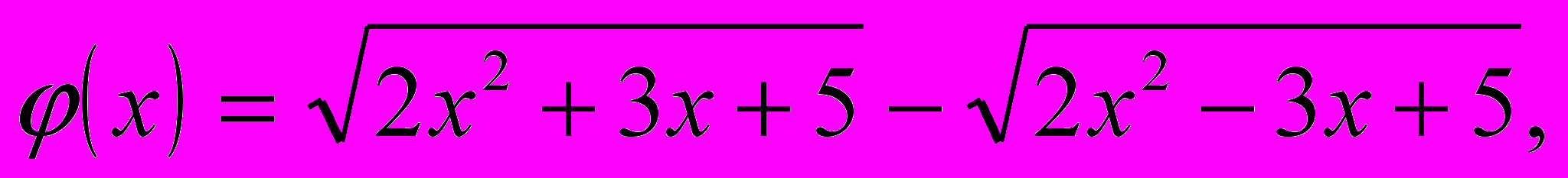
сопряжённое выражению
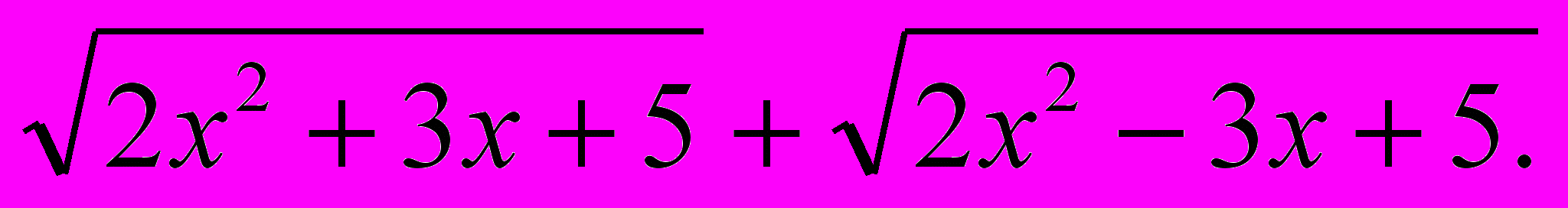
Так как
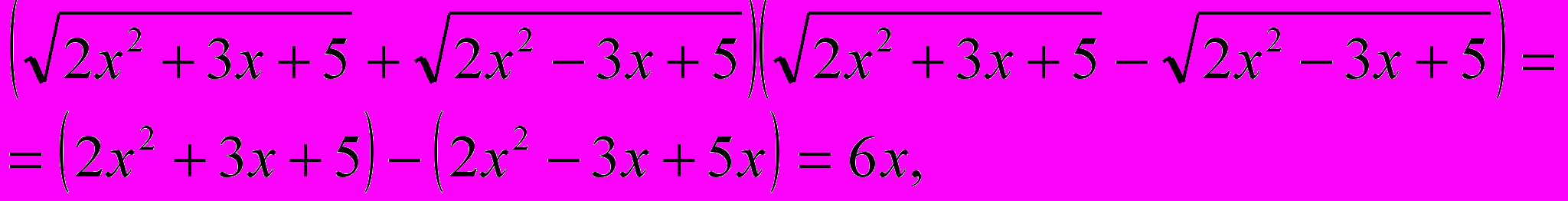
То уравнение (1) примет вид:
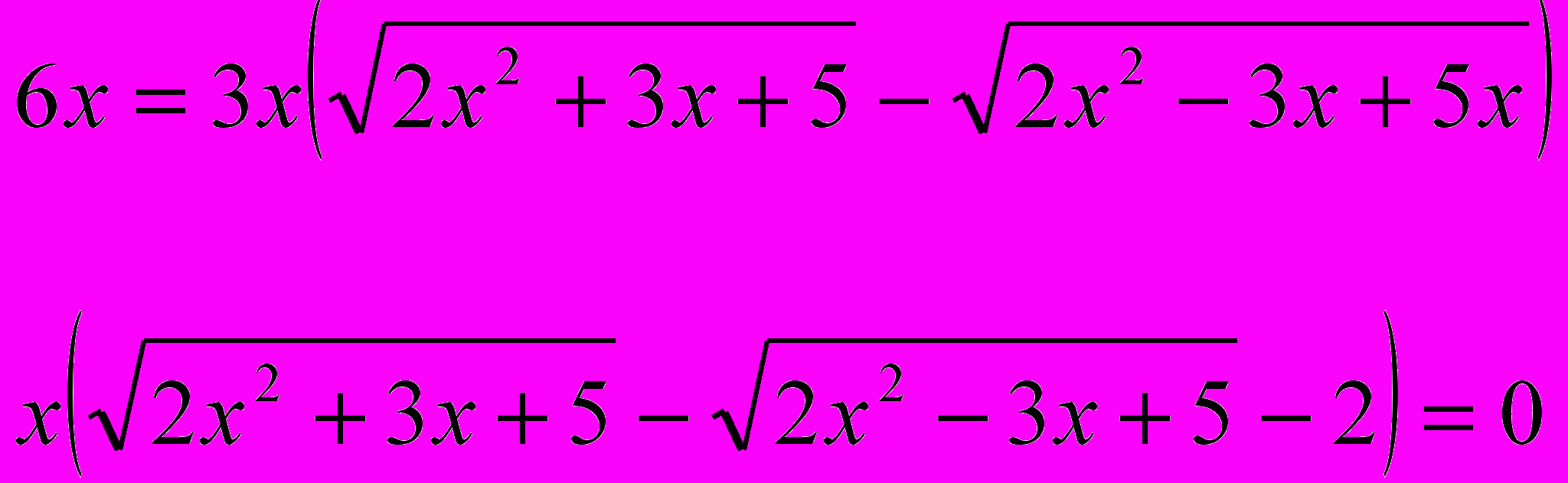
Или
Произведение равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю, а другой при этом известен. Тогда x1=0.Остаётся решить уравнение:
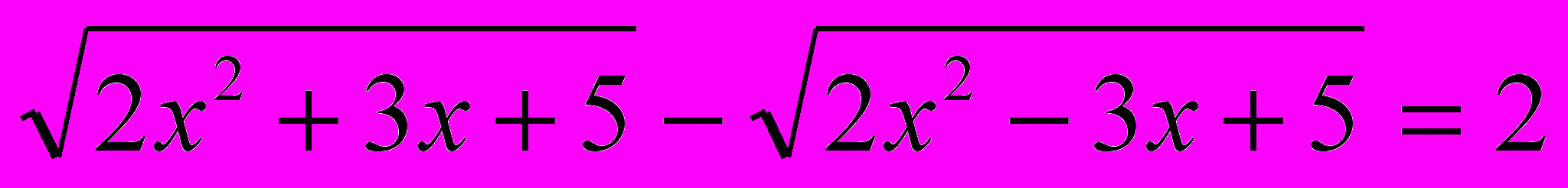
(2)
Сложив уравнения (1) и (2), придём к уравнению
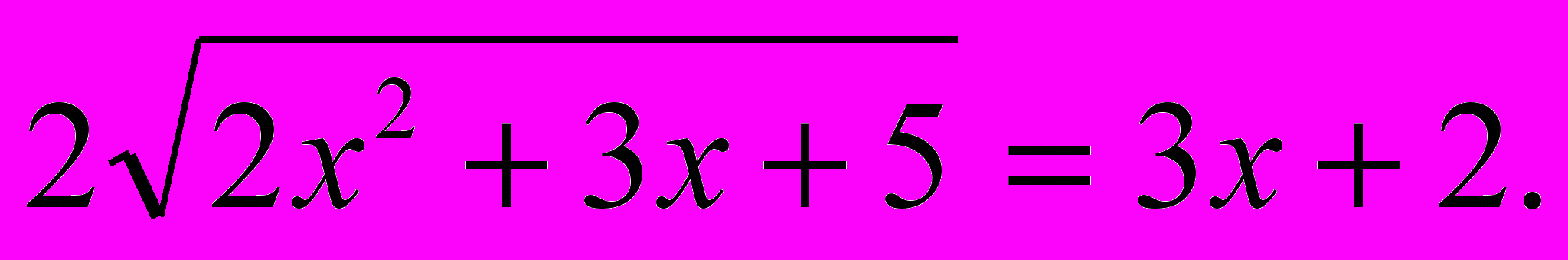
(3)
Решая уравнение (3) методом возведения в квадрат, получим:

Проверка:
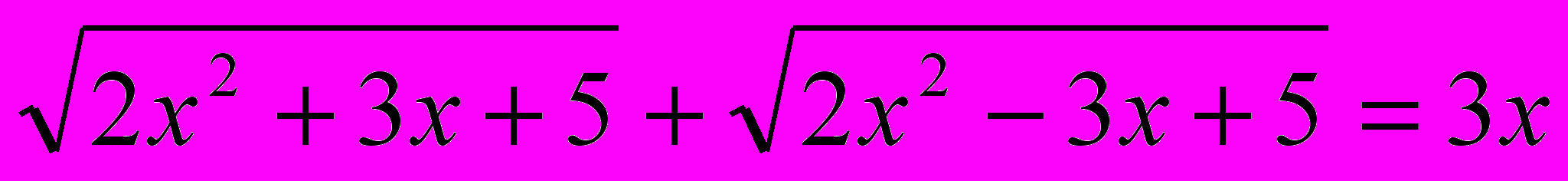
x1=0, x2=4, x3= -4 подставим в уравнение
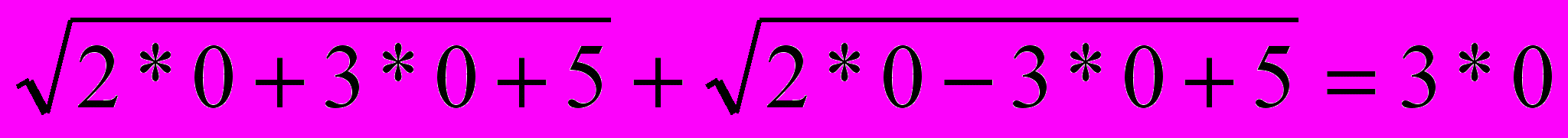
1)
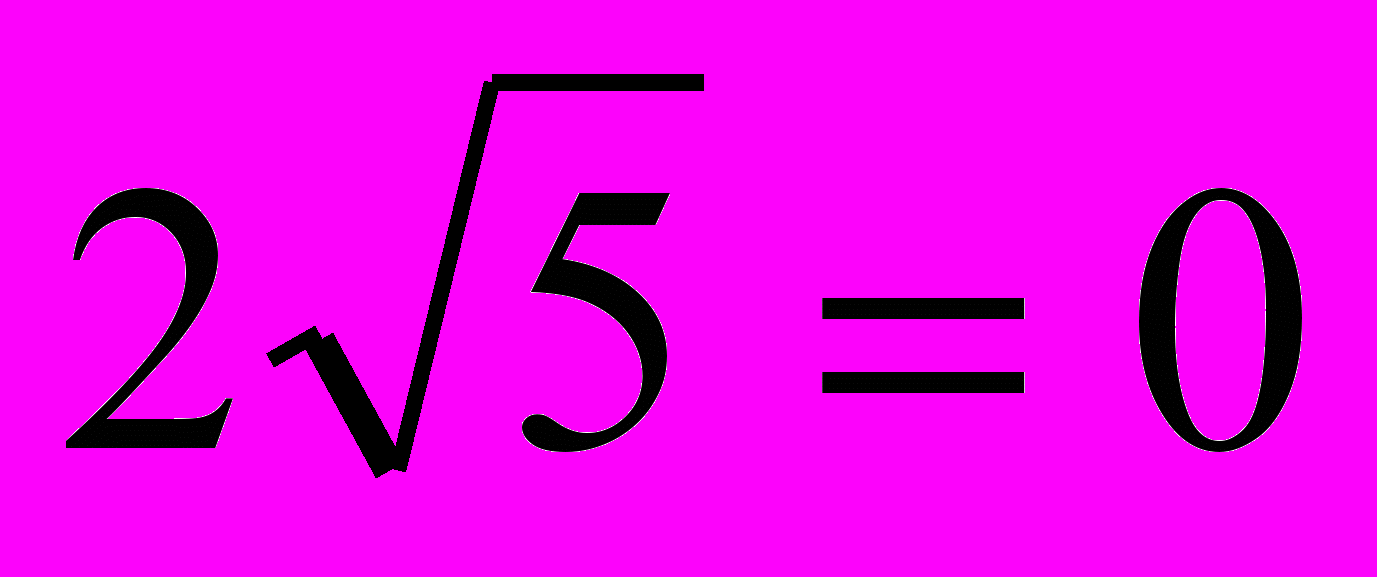
- не верное равенство, значит x1=0- не корень уравнения.
2
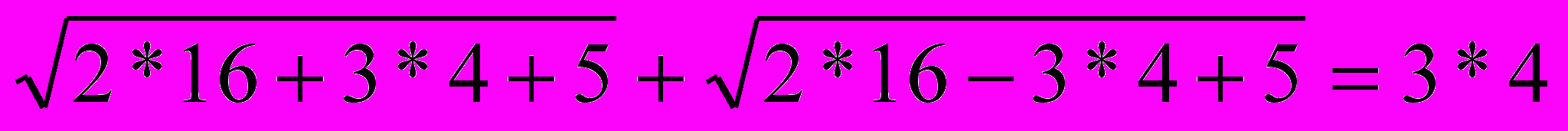 )
)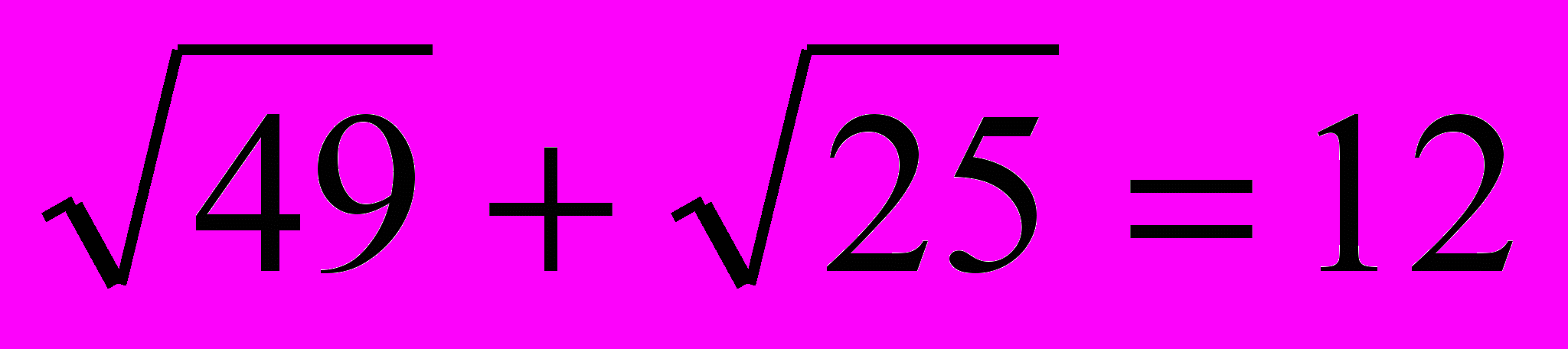
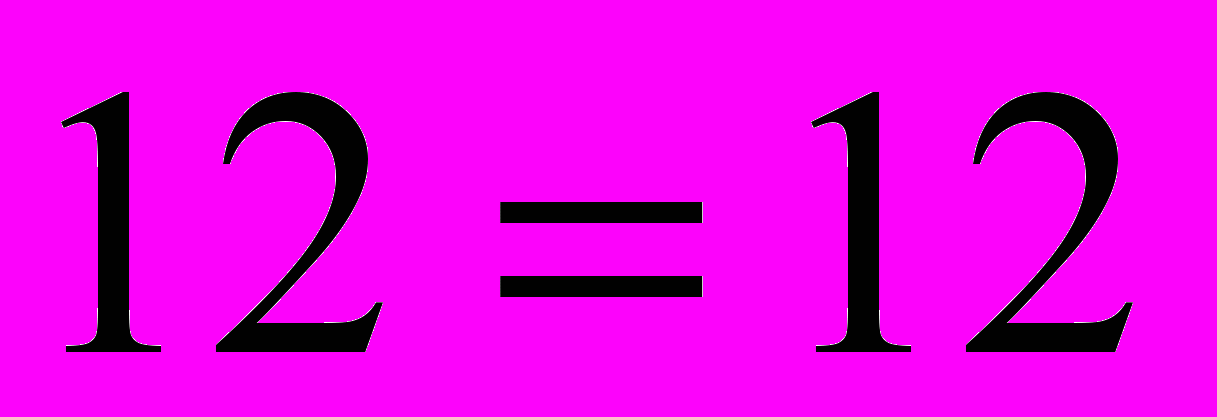 - верное равенство, значит x2=4- корень уравнения.
- верное равенство, значит x2=4- корень уравнения.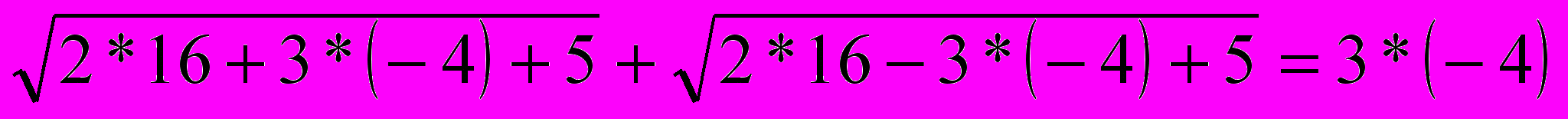
3)
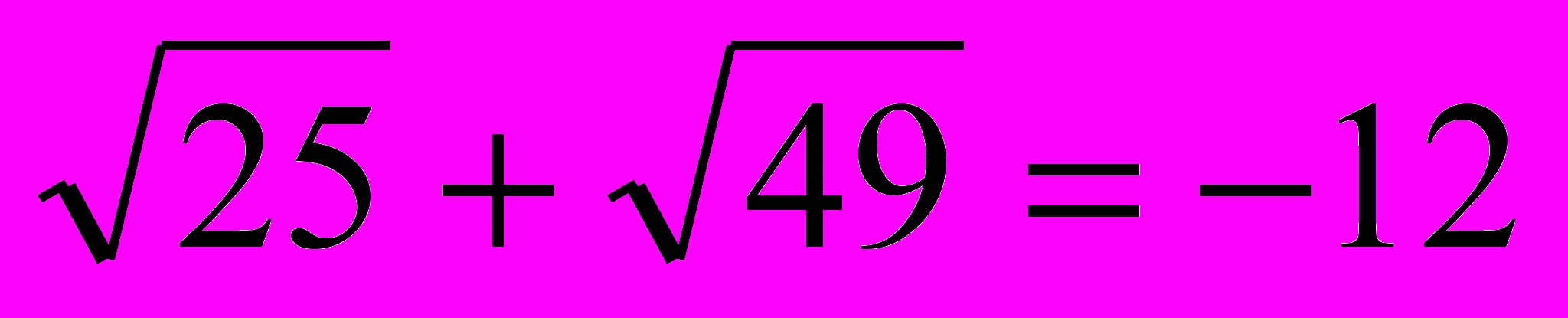
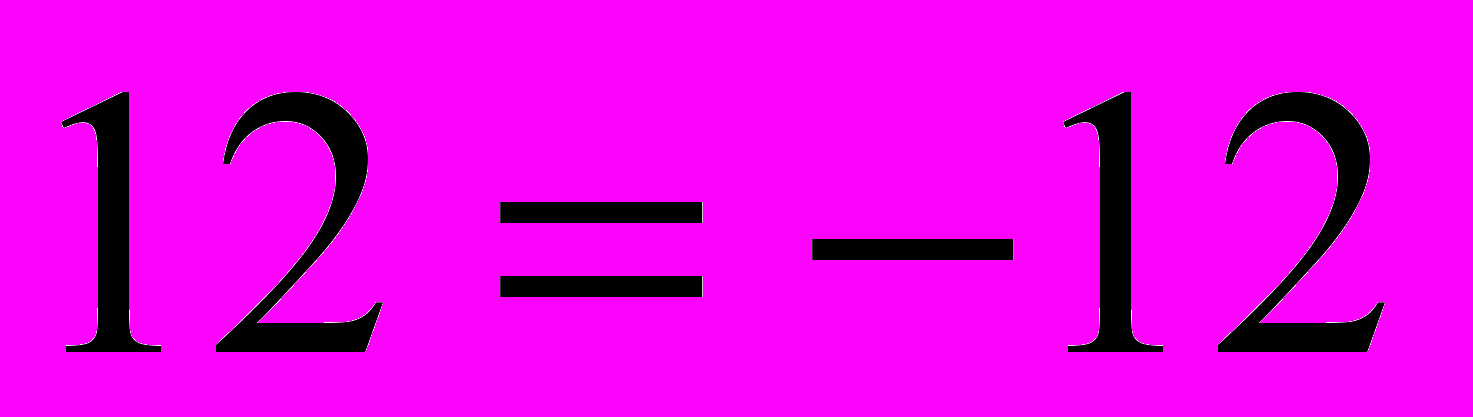
- не верное равенство, значит x3= -4- не корень уравнения.
Ответ: 4.
ЗАКЛЮЧЕНИЕ
Итак, уравнения, которые содержат переменную под знаком корня, называются иррациональными. Иррациональные уравнения решаются в основном возведением обеих частей уравнения в квадрат (или n-ую степень) или введением новой переменной. Кроме того, пользуются и искусственными приемами решения иррациональных уравнений.
 Иррациональные неравенства
Иррациональные неравенства 
 |  |  |
| | Если в неравенство входят функции под знаком корня, то такие неравенства называют иррациональными. |  |
 |  |  |
| | ||
Стандартный метод решения этих неравенств заключается в возведении обеих частей неравенства в нужную степень: если в неравенство входит квадратный корень, то в квадрат; входит корень третьей степени − в куб и т. д. Однако, преобразования неравенств, возводить в квадрат, не нарушая равносильности, можно только неравенство, у которого обе части неотрицательны. При возведении же в квадрат неравенств, части которых имеют разные знаки, могут получиться неравенства, как равносильные исходному, так и неравносильные ему. Простой пример: –1 < 3 − верное неравенство,
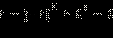 − тоже верное неравенство. Несмотря на то, что –4 < –1 − неравенство верное, неравенство
− тоже верное неравенство. Несмотря на то, что –4 < –1 − неравенство верное, неравенство  уже верным не является.
уже верным не является. Покажем, как получить равносильные системы для некоторых часто встречающихся типов неравенств.
Неравенства вида
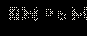
Если x лежит в ОДЗ: f (x) ≥ 0, то левая часть неравенства существует и неотрицательна. Поскольку для всех x, являющихся решением данного неравенства, правая часть больше левой, то g (x) > 0. Следовательно, обе части неравенства неотрицательны (для тех x, которые являются решениями неравенства, другие x нас не интересуют). Значит, возведение в квадрат не нарушает равносильности и можно записать равносильную нашему неравенству систему неравенств:
 |
Пример 1
Решите неравенство
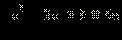
Решение.
| Сразу перейдём к равносильной системе:
Ответ. 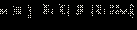 |
Пример 2
Решите неравенство
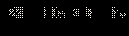
Решение.
| Перейдём к равносильной системе:
Ответ.  |
Неравенства вида
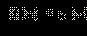
ОДЗ данного неравенства f (x) ≥ 0. Пусть для каких-то x из ОДЗ g (x) < 0. Тогда, очевидно, все эти x − решения, так как при этих x левая часть определена (x
 ОДЗ) и неотрицательна, в то время как правая часть g (x) < 0.
ОДЗ) и неотрицательна, в то время как правая часть g (x) < 0.Для других x из ОДЗ g (x) ≥ 0. Для них обе части неравенства неотрицательны, и его можно возвести в квадрат:
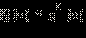 Значит, данное неравенство равносильно совокупности неравенств:
Значит, данное неравенство равносильно совокупности неравенств: 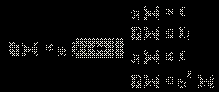 |
Заметим, что в последнюю систему не входит требование f (x) ≥ 0. Оно и не нужно, так как выполняется автоматически
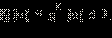 ибо полный квадрат всегда неотрицателен.
ибо полный квадрат всегда неотрицателен.Пример 3
Решите неравенство
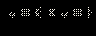
 Решение.
Решение.| ОДЗ неравенства: x ≥ –3. 1. Если  то все эти x то все эти x  ОДЗ, для которых верно x < –1, − решения. Таким образом, ОДЗ, для которых верно x < –1, − решения. Таким образом, 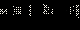 − первая часть ответа. − первая часть ответа.2. Если  то обе части неравенства неотрицательны, и его можно возвести в квадрат. Имеем: то обе части неравенства неотрицательны, и его можно возвести в квадрат. Имеем:
Получаем, что решениями являются все 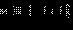 Объединяя результаты пунктов 1 и 2, получаем: Ответ. 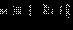 |
Пример 4
Решите неравенство
Решение.
| ОДЗ данного неравенства:  Будем рассматривать только эти x, другие x не могут являться решениями данного неравенства. Будем рассматривать только эти x, другие x не могут являться решениями данного неравенства.1. Если  то есть то есть 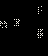 то все такие x из ОДЗ, удовлетворяющие этому условию, являются решениями неравенства. Значит, все x ≤ –3 − решения неравенства. то все такие x из ОДЗ, удовлетворяющие этому условию, являются решениями неравенства. Значит, все x ≤ –3 − решения неравенства.2. Если  то есть то есть  а с учетом ОДЗ это означает, что а с учетом ОДЗ это означает, что 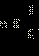 то обе части неравенства неотрицательны. Возведём обе части неравенства в квадрат: то обе части неравенства неотрицательны. Возведём обе части неравенства в квадрат:
Уравнение 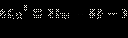 имеет корни имеет корни  и и  Значит, решением неравенства являются Значит, решением неравенства являются  С учётом С учётом 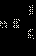 получается, что на данном множестве решениями являются получается, что на данном множестве решениями являются  Объединяя результаты пунктов 1 и 2, получаем Объединяя результаты пунктов 1 и 2, получаем Запишем это решение другим способом:
Ответ.  |
Неравенства вида
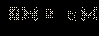
ОДЗ данного неравенства:
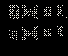 Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему
Обе части неравенства неотрицательны в ОДЗ, и потому можно возводить в квадрат. Получим равносильную систему  |
Заметим, что из неравенства
 следует, что
следует, что 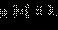 то есть дополнительно это требовать и включать это неравенство в систему не нужно.
то есть дополнительно это требовать и включать это неравенство в систему не нужно.Отметим полезное следствие. Предположим, что ОДЗ неравенства уже найдено, и мы будем отбирать решения только из ОДЗ (это разумно, поскольку вне ОДЗ решений нет). Тогда исходное неравенство равносильно следующему:
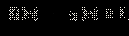 а та система, которой это неравенство равносильно, может быть представлена (для x из ОДЗ) в виде
а та система, которой это неравенство равносильно, может быть представлена (для x из ОДЗ) в виде 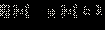 Следовательно, в ОДЗ
Следовательно, в ОДЗ  |
Ясно, что те же рассуждения применимы и для знака неравенства ≥. Отсюда можно сделать полезное заключение:
Знак разности
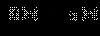 совпадает со знаком выражения
совпадает со знаком выражения 
Отсюда же получается ещё одно полезное следствие:
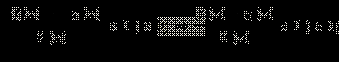 в ОДЗ:
в ОДЗ: 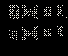
Пример 5
Решите неравенство
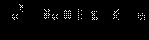
Решение.
| Перейдём к равносильной системе:
Решая эту систему методом интервалов, сразу получаем: Ответ. 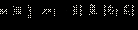 |
Пример 6
Решите неравенство
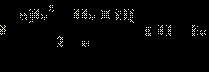
Решение.
| ОДЗ данного неравенства: 
Заметим, что в ОДЗ x ≥ 0, поэтому существует 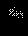 и значит, и значит,
Мы воспользовались здесь тем, что в ОДЗ x ≥ 0, (x – 5)(x – 6) ≥ 0 и потому существуют выписанные в последней строчке корни. Кроме того, мы вынесли за скобку 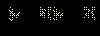 который по вышесказанному существует. Этот корень неотрицателен и потому не влияет на знак неравенства, следовательно, на него можно сократить, не забывая, что он может ещё обратиться в нуль и те x, для которых корень обращается в нуль, являются решениями неравенства. Таким образом, в ответ необходимо включить число x = 5. При x = 6 корень который по вышесказанному существует. Этот корень неотрицателен и потому не влияет на знак неравенства, следовательно, на него можно сократить, не забывая, что он может ещё обратиться в нуль и те x, для которых корень обращается в нуль, являются решениями неравенства. Таким образом, в ответ необходимо включить число x = 5. При x = 6 корень 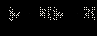 обращается в нуль, но x = 6 не входит в ОДЗ неравенства. Воспользуемся теперь тем, что знак разности корней совпадает со знаком разности подкоренных выражений. Имеем: обращается в нуль, но x = 6 не входит в ОДЗ неравенства. Воспользуемся теперь тем, что знак разности корней совпадает со знаком разности подкоренных выражений. Имеем:
Учтём теперь ОДЗ и получим: Ответ.  |
Неравенства вида
ОДЗ данного неравенства:
 Предположим, что функции f (x) и g (x) не имеют общих корней. Рассмотрим вспомогательное неравенство
Предположим, что функции f (x) и g (x) не имеют общих корней. Рассмотрим вспомогательное неравенство | |  | (*) |
1. Если g (x) < 0, то для любого x из ОДЗ выполнено
2. Если g (x) ≥ 0, то выражение
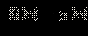 может иметь любой знак, но выражение
может иметь любой знак, но выражение 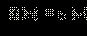 всегда строго положительно. Умножая обе части неравенства (*) на строго положительное число
всегда строго положительно. Умножая обе части неравенства (*) на строго положительное число 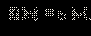 не меняя знака неравенства, перейдём к равносильному неравенству
не меняя знака неравенства, перейдём к равносильному неравенству  |
Таким образом, в ОДЗ
 |
Значит, при g (x) ≥ 0, знак разности
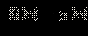 совпадает со знаком разности
совпадает со знаком разности 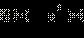 в ОДЗ.
в ОДЗ.Получаем следующие условия равносильности.
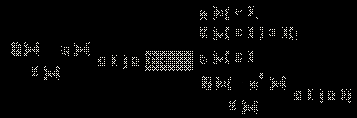 |
Запоминать приведённые системы неравенств не нужно, важно понимать, как они получаются.
Пример 7
Решите неравенство
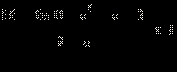
Решение.
| Выполним равносильные в ОДЗ преобразования и приведём неравенство к удобному для применения результатов настоящего пункта виду.
Мы не случайно сделали последнее преобразование. Важно понимать, чему здесь конкретно равняется функция g (x) = 2x – 8. Типичной ошибкой является считать, что g (x) = 2x + 8. ОДЗ данного неравенства: 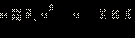 то есть то есть 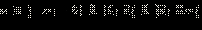 Теперь перейдём к равносильной системе. В ОДЗ Теперь перейдём к равносильной системе. В ОДЗ
С учётом ОДЗ сразу получаем: Ответ.  |
^ СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ.
1) А.Г.Мордкович. Алгебра 8 класс. Учебник для общеобразовательных учреждений - Москва: Издательство «Мнемозина», 1999.
2) М.Я.Выгодский. Справочник по элементарной математике - Москва: Издательство «Наука», 1986.
3) А.П.Савин. Энциклопедический словарь юного математика – Москва: Издательство «Педагогика», 1989.
4) А.И.Макушевич. Детская энциклопедия – Москва: Издательство «Педагогика», 1972.
5) Н.Я.Виленкин. Алгебра для 9 класс. Учебное пособие для учащихся школ и классов с углубленным изучением изучением математики – Москва: Издательство «Просвещение», 1998.