Дифференциальные эллиптические уравнения второго порядка. Слабое решение. Обобщенное решение задачи Дирихле
| Вид материала | Решение |
- Дифференциальные уравнения (вопросы к экзамену), 26.43kb.
- Календарный план чтения лекций, 27.51kb.
- Найти частное решение линейного однородного дифференциального уравнения. Решение, 6.09kb.
- Уравнения математической физики направление подготовки, 18.02kb.
- Решение дифференциального уравнения первого и второго порядка методом Рунге-Кутта 4-го, 55.71kb.
- Вопросы к экзамену по математике для студентов заочного отделения, 19.65kb.
- Задача Коши для неоднородного уравнения с однородными граничными условиями, 80.58kb.
- Обыкновенные дифференциальные уравнения, 17.54kb.
- Курсовая работа «Дифференциальные уравнения» Задача №1 (3 задачи), 8.81kb.
- Программа-минимум кандидатского экзамена по специальности 01. 01. 02 «Дифференциальные, 37.38kb.
Тема 4
Дифференциальные эллиптические уравнения второго порядка. Слабое решение. Обобщенное решение задачи Дирихле.
Оператор Лапласа, который мы рассматривали в предыдущей теме,
можно записать так:
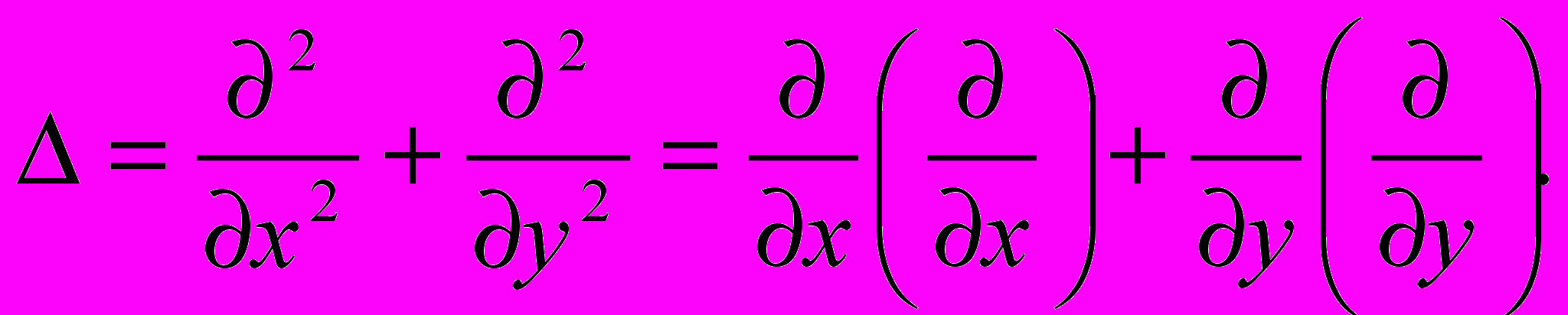
А если обозначить x=x1, y=x2, то так:
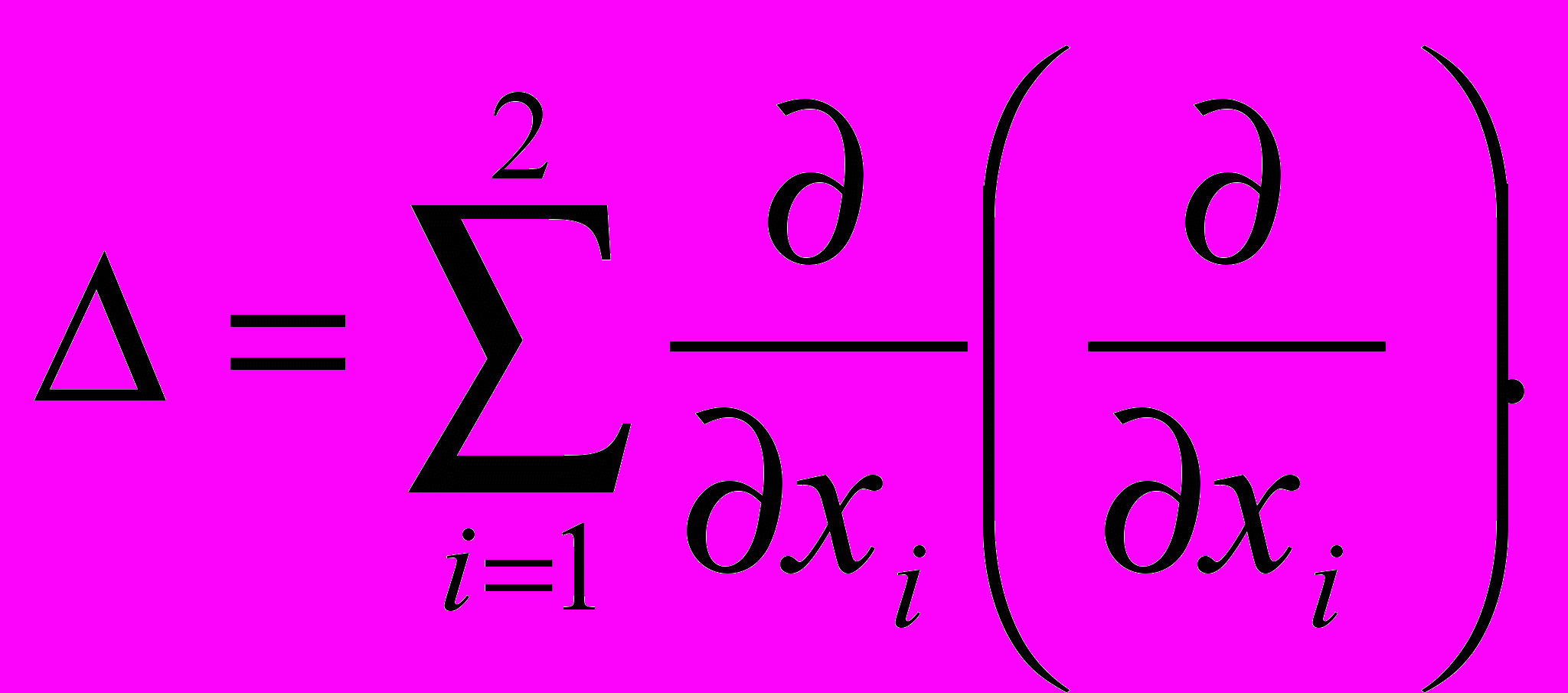
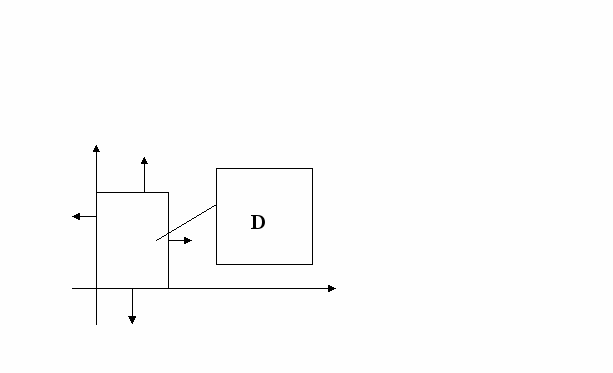
В прямоугольнике D, изображенном на рисунке, рассмотрим дифференциальное уравнение второго порядка
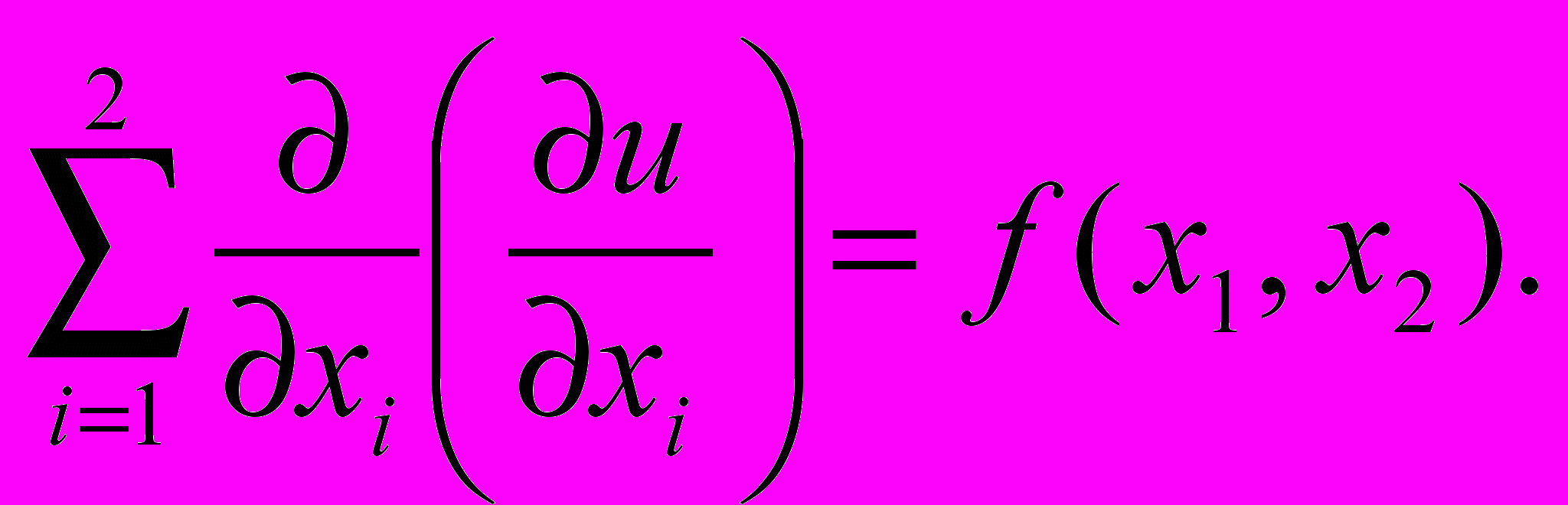 /1/
/1/Для простоты предположим, что функция f бесконечно дифференцируемая.
Пусть в прямоугольнике D
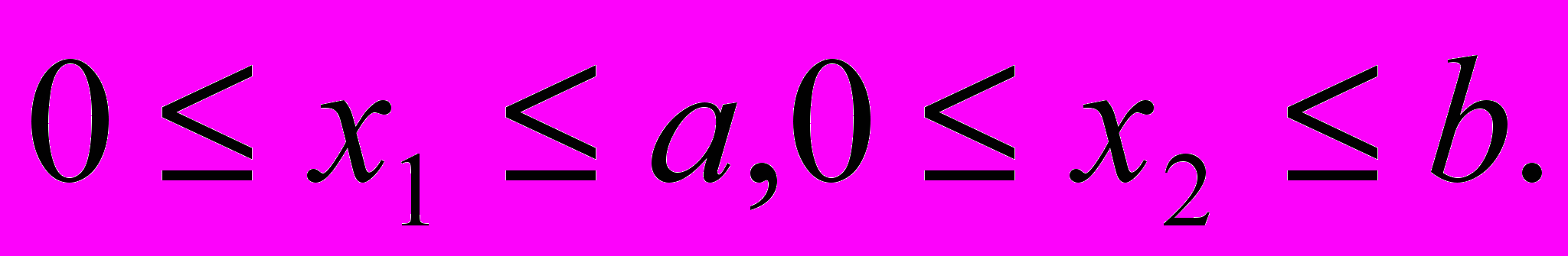
Пусть (x1, x2)- бесконечно дифференцируемая функция, которая обращается в нуль
в некоторой окрестности границы прямоугольника D. Умножим обе части уравнения /1/
на функцию (x1, x2) и проинтегрируем по прямоугольнику D:
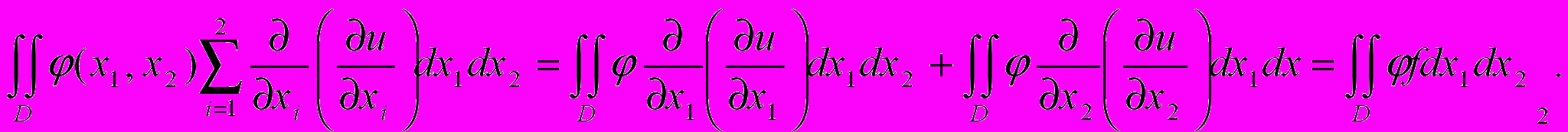
Вычислим сначала, применяя формулу интегрирования по частям, интеграл
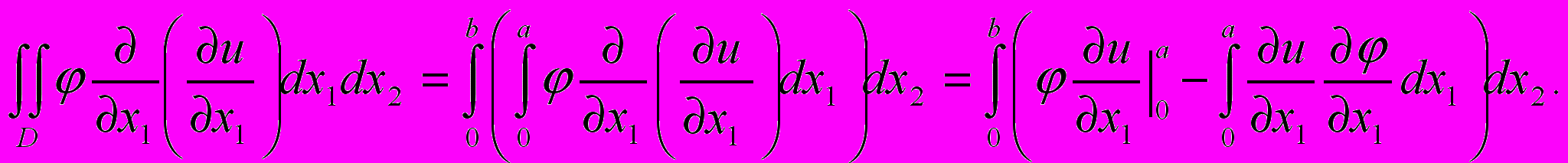
Поскольку функция обращается в нуль на границе области D, в правой части этого равенства под знаком внешнего интеграла пропадет первое слагаемое. Аналогично получим, что

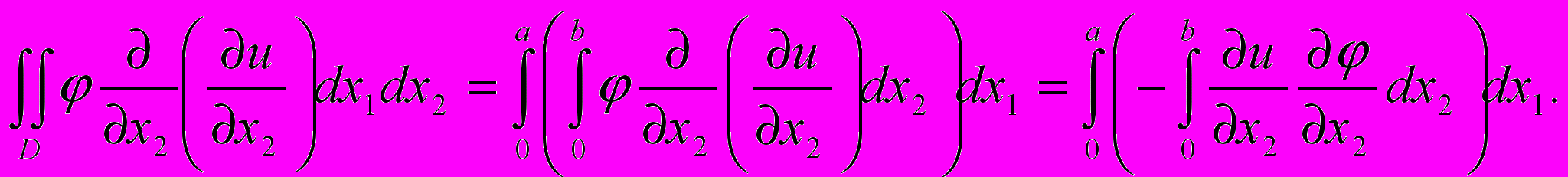
Итак, мы показали, что
 /2/
/2/ если =0 в окрестности границы прямоугольника D.
Формула /2/ сохраняется, если D- любая ограниченная область на плоскости Ox1x2
с «хорошей» границей.
Если функция не обращается в нуль в окрестности границы
такой области, то справедлива формула Грина

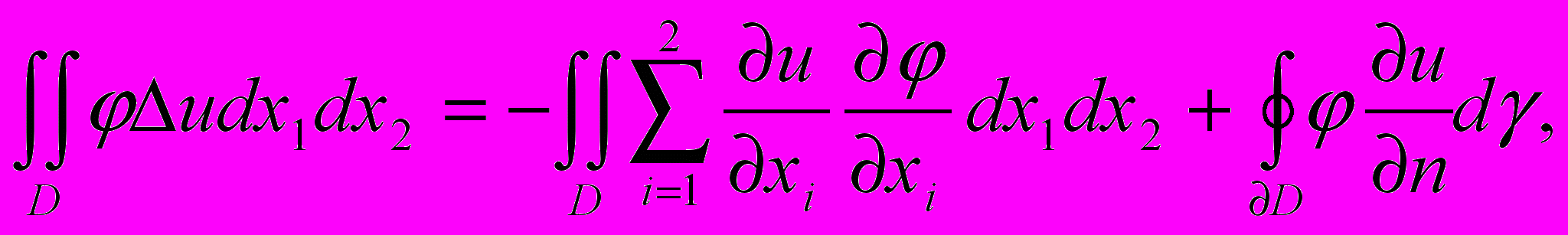 где D- граница области D, d- элемент длины дуги этой границы, а
где D- граница области D, d- элемент длины дуги этой границы, а 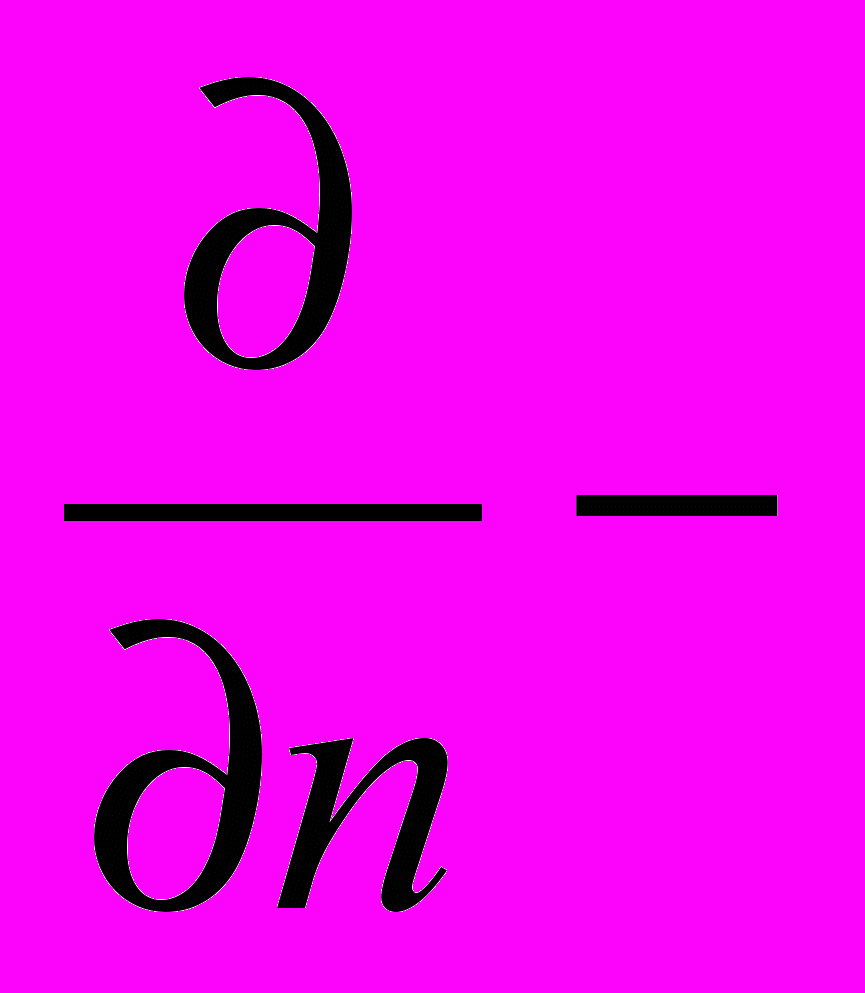 производная по внешней нормали к D.
производная по внешней нормали к D.Рассмотрим вместо уравнения /1/
 с постоянными коэффициентами
с постоянными коэффициентамиуравнение с переменными коэффициентами


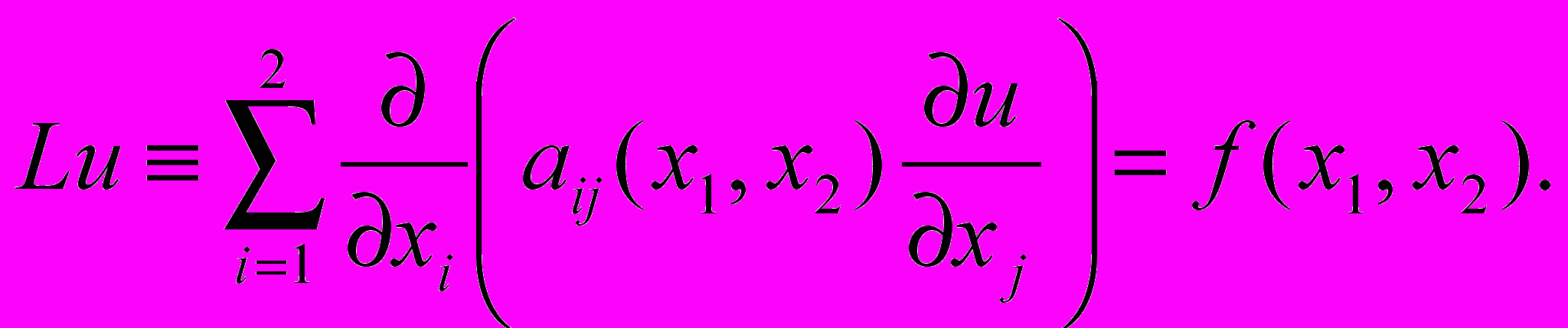 /3/
/3/Будем считать, что
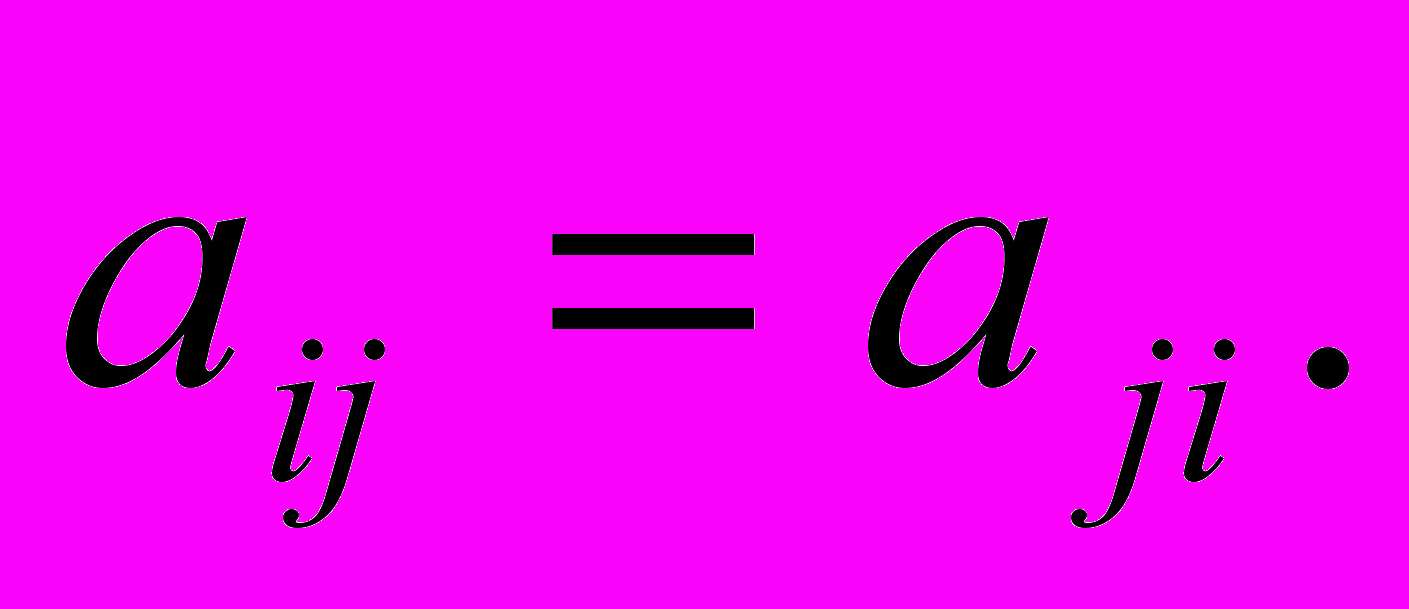
Имеем:
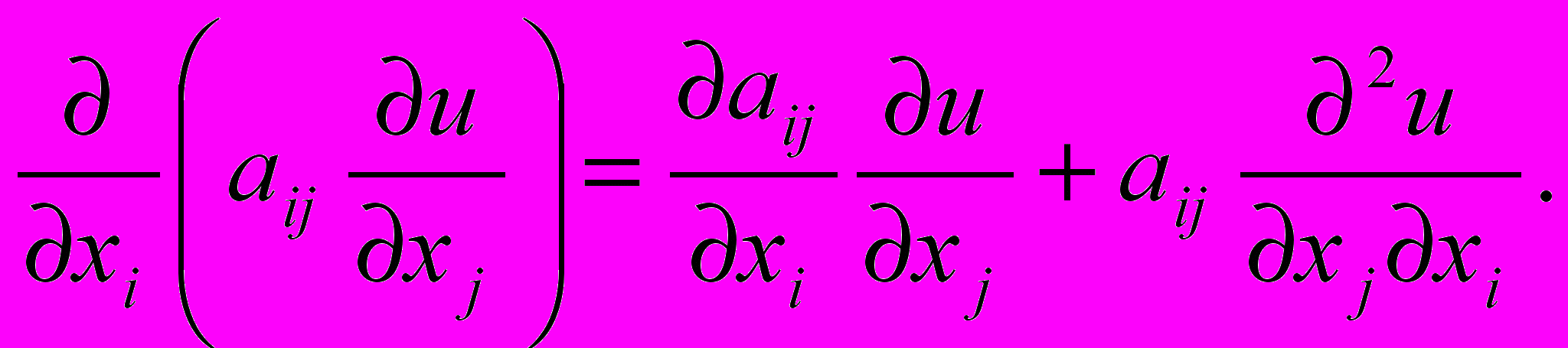 Следовательно, в уравнение /3/ входят частные производные функции u(x1, x2) первого и второго порядков, коэффициенты
Следовательно, в уравнение /3/ входят частные производные функции u(x1, x2) первого и второго порядков, коэффициенты  и их производные. Значит, для того чтобы функция u(x1, x2) была бы решением уравнения /3/
и их производные. Значит, для того чтобы функция u(x1, x2) была бы решением уравнения /3/в обычном смысле (то есть если рассматривать его классическое решение ) надо, чтобы эта функция обладала непрерывными частными производными до второго порядка включительно, а коэффициенты имели непрерывные частные производные первого порядка.
Дадим определение э л л и п т и ч е с к о г о дифференциального уравнения.
Пусть уравнение /3/ рассматривается в некоторой ограниченной области D на плоскости
Oxy (в других обозначениях Ox1x2). Выделим в левой части уравнения /3/ слагаемые, содержащие только производные второго порядка от функции u(x1, x2):

Формально составим многочлен

Будем рассматривать только такие уравнения /3/, что для любой фиксированной точки
(x1, x2)D этот многочлен положителен при любых значениях 1, 2 ,
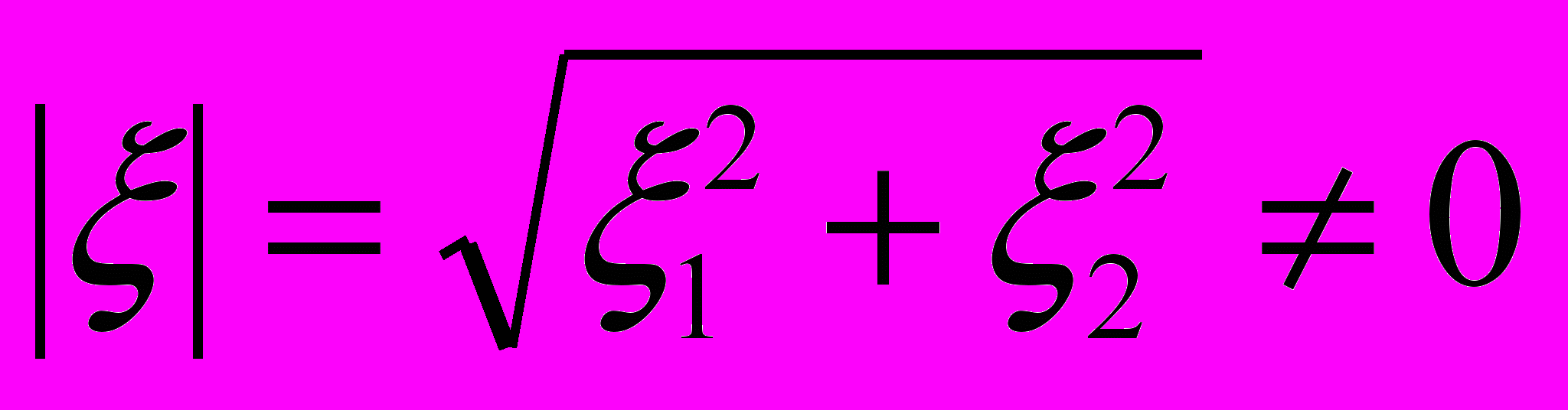 .
.Уравнение /3/, для которого указанное свойство выполнено, называется эллиптическим уравнением в области D.
Подробная классификация дифференциальных уравнений второго порядка (эллиптических, гиперболических, параболических) будет дана ниже в теме 7.
По этому определению уравнение u=f, рассмотренное ранее, является эллиптическим.
Действительно, заменим в


 на 11=
на 11=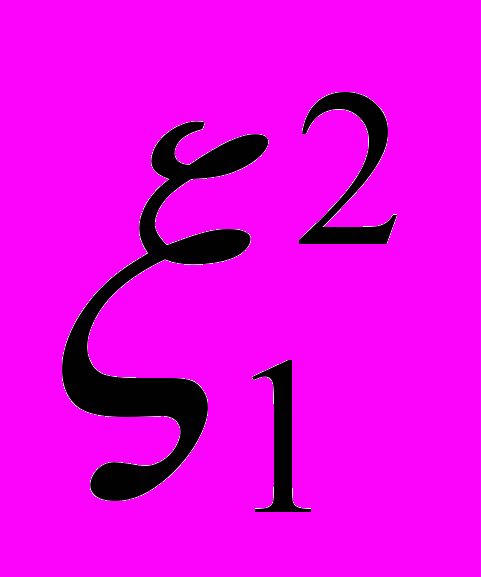 , а
, а 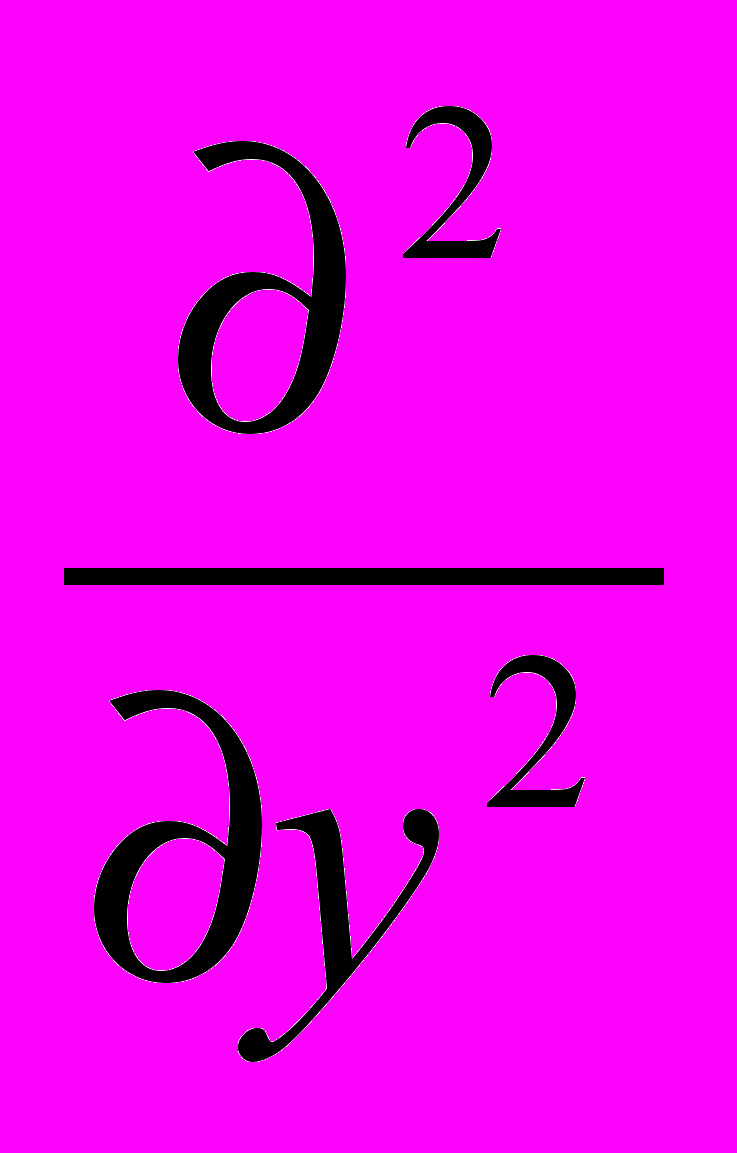 на 22
на 22 и рассмотрим многочлен второго порядка по 1, 2 :
и рассмотрим многочлен второго порядка по 1, 2 : 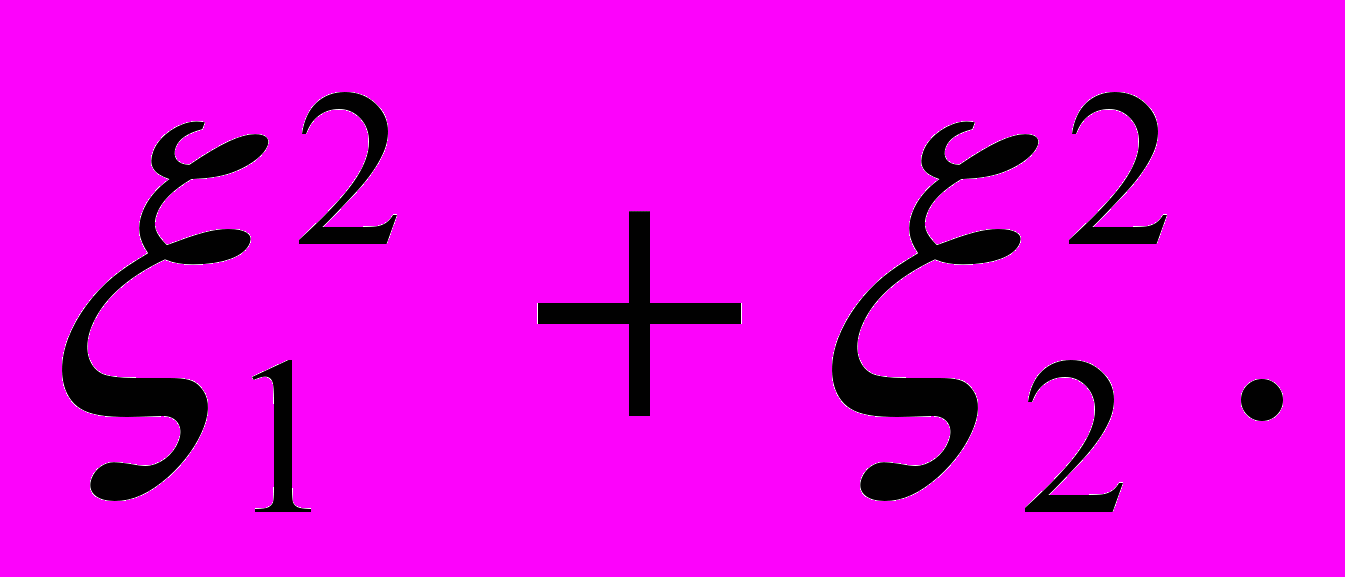 Этот многочлен отличен от нуля при любых значениях 1, 2 , ||0.
Этот многочлен отличен от нуля при любых значениях 1, 2 , ||0.Для уравнения /3/ справедлива формула, аналогичная формуле /2/, которую мы получили
в случае уравнения u=f:
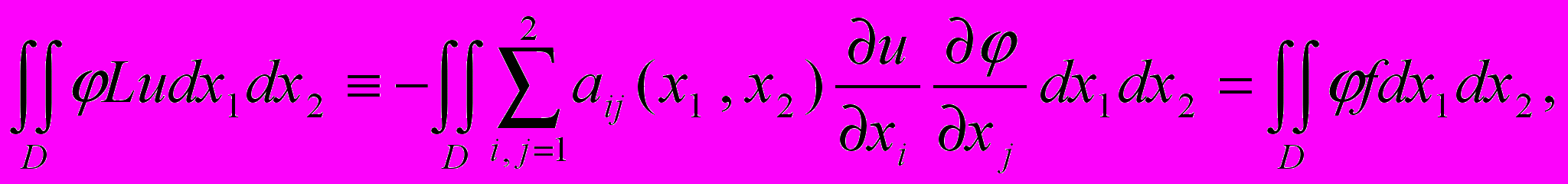 /4/
/4/ если функция (x1, x2) обращается в нуль в некоторой окрестности границы области D.
Если функция u(x1, x2) имеет непрерывные частные производные первого и второго порядков, а функция (x1, x2) бесконечно дифференцируемая и обращается в нуль в окрестности границы области D, то из справедливости тождества /2/ следует, что u(x1, x2)
удовлетворяет уравнению /1/. То же верно и для /4/ и уравнения /3/: при достаточно «хороших» u(x1, x2), aij и (x1, x2) из /4/ следует /3/.
Таким образом, сказать, что u(x1, x2) удовлетворяет уравнению /3/или, что u(x1, x2) удовлетворяет тождеству /4/- одно и то же. Этот факт ляжет в основу определения слабого (уже не классического) решения эллиптического уравнения /3/.
Заметим, что интегральное тождество /4/ имеет преимущество перед уравнением /3/:
в /4/ коэффициенты аij входят непосредственно, без своих производных, а от функции u(x1, x2) в /4/ входят только частные производные первого ( не второго) порядка. Более слабые, чем для справедливости /3/, требования на коэффициенты и функцию u(x1, x2)
больше соответствуют смыслу задач прикладного характера, приводящих к эллиптическим дифференциальным уравнениям второго порядка. Поясним это на примере.
Пусть пластина D неравномерно нагрета с температурой u(x1, x2, t) в точке (x1, x2) в момент времени t. Пусть часть границы D этой пластины подогревается. Если процесс установился, то температура уже не меняется во времени, только- от точки к точке, то есть
u=u(x1, x2). Пусть к- коэффициент теплопроводности, который зависит от точки (x1, x2),
но не зависит от направления. В этом случае говорят, что пластина D изотропна. Можно показать, что температура u(x1, x2) удовлетворяет уравнению
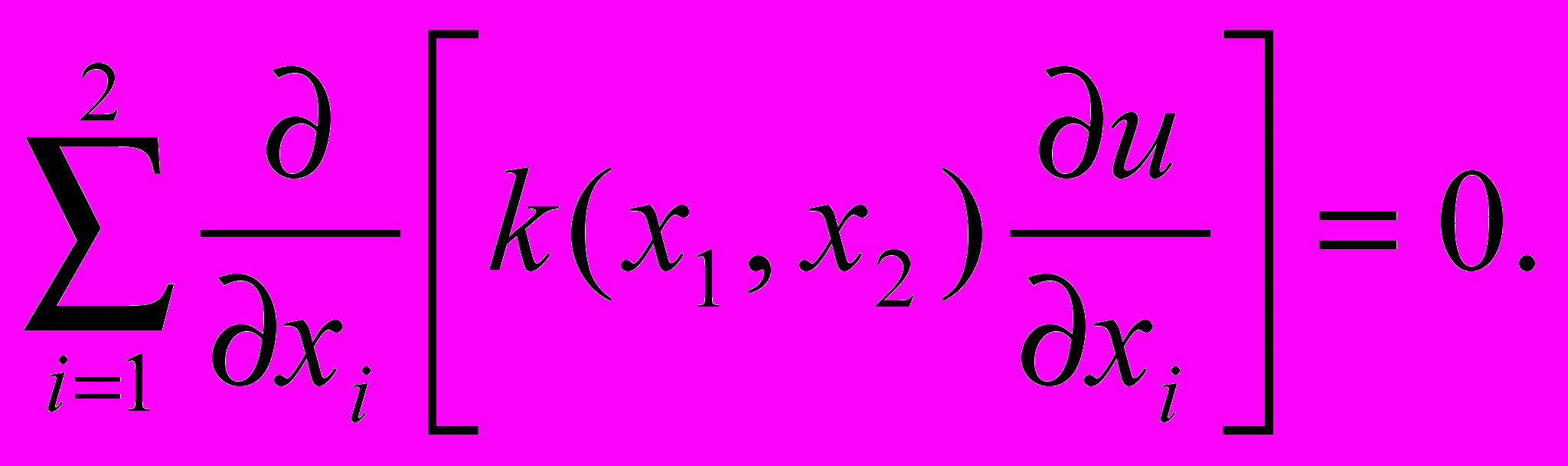 /5/
/5/Имеем:
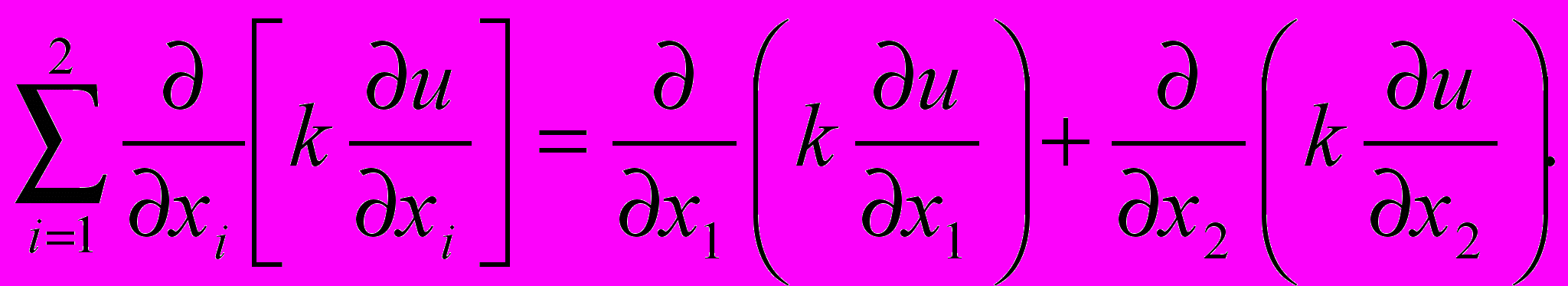
Можно ли считать в этой физической задаче, что всюду в D коэффициент теплопроводности к имеет частные производные первого порядка? Сейчас мы покажем, что не всегда. Конкретизируем задачу. Пусть пластина (область) D разбита на две подобласти D1и D2 гладкой кривой . Пусть коэффициент теплопроводности постоянен в каждой из этих подобластей и равен постоянной к1 в D1 и постоянной к2 в D2, причем к1к2 (то есть коэффициент теплопроводности рвется на ).
Поскольку к1- постоянная, уравнение /5/ в области D1 превращается в уравнение Лапласа
u=0. То же- и в области D2. Из физических соображений на должны выполняться условия: 1) температура u(x1, x2) непрерывна; 2) теплового баланса, то есть если u=u1 в D1,
u=u2 в D2, то
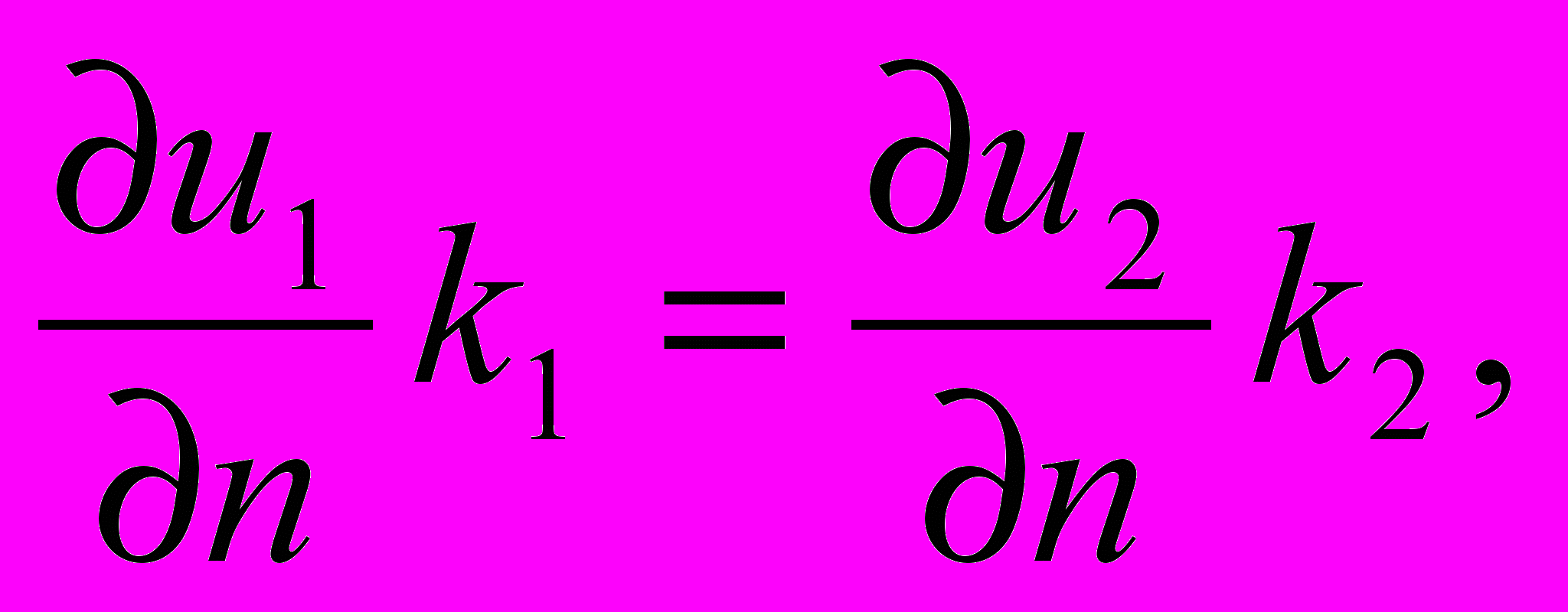 где n- нормаль к .
где n- нормаль к .Поскольку по условию к1к2, то из 2) следует, что
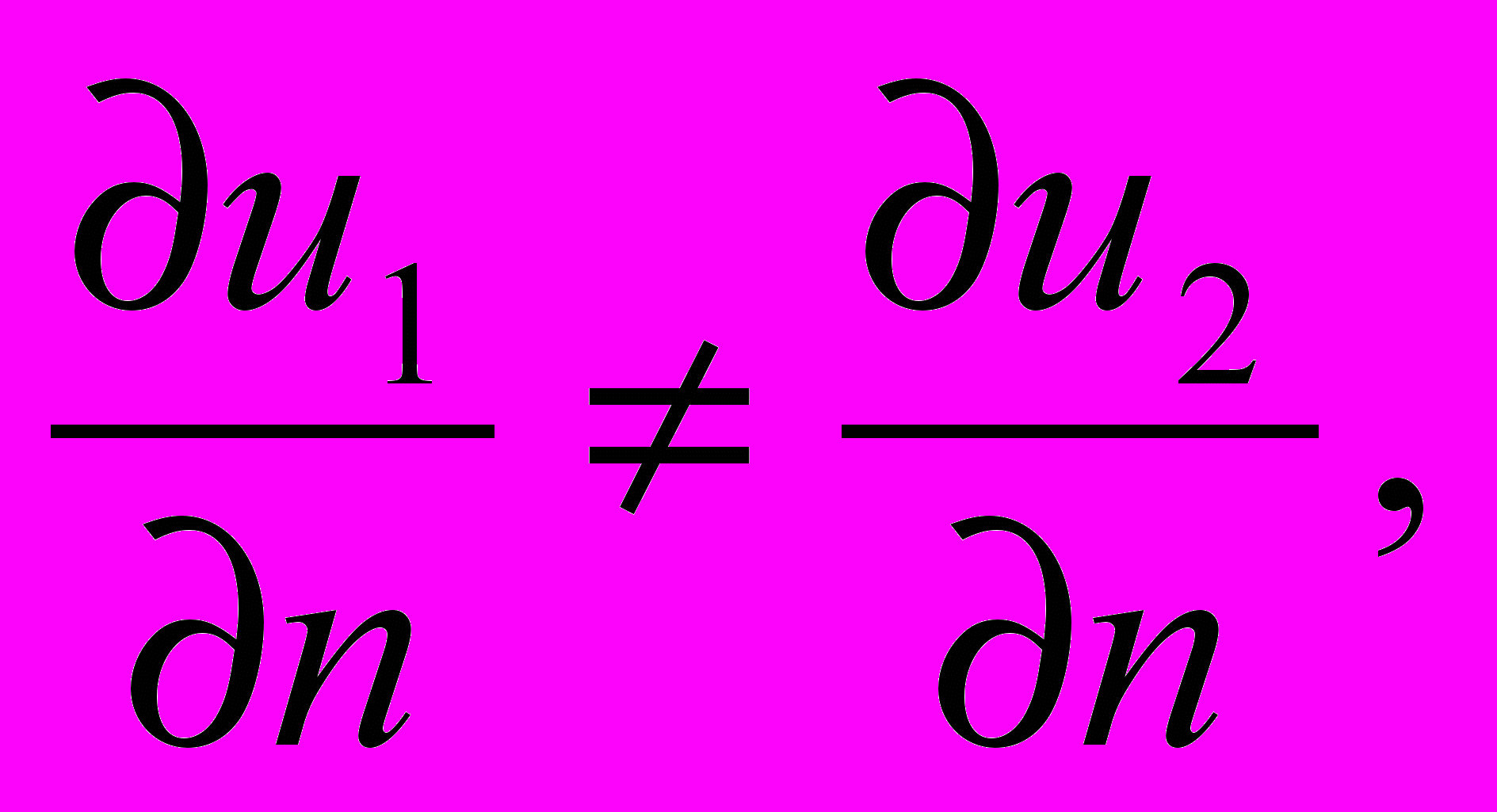 так что производные функции u(x1, x2) рвутся на . Поэтому функция u(x1, x2) не может быть классическим решением уравнения /5/ в области D.
так что производные функции u(x1, x2) рвутся на . Поэтому функция u(x1, x2) не может быть классическим решением уравнения /5/ в области D.В то же время покажем, что эта функция удовлетворяет интегральному тождеству /4/.
Для бесконечно дифференцируемой в области D функции имеем:
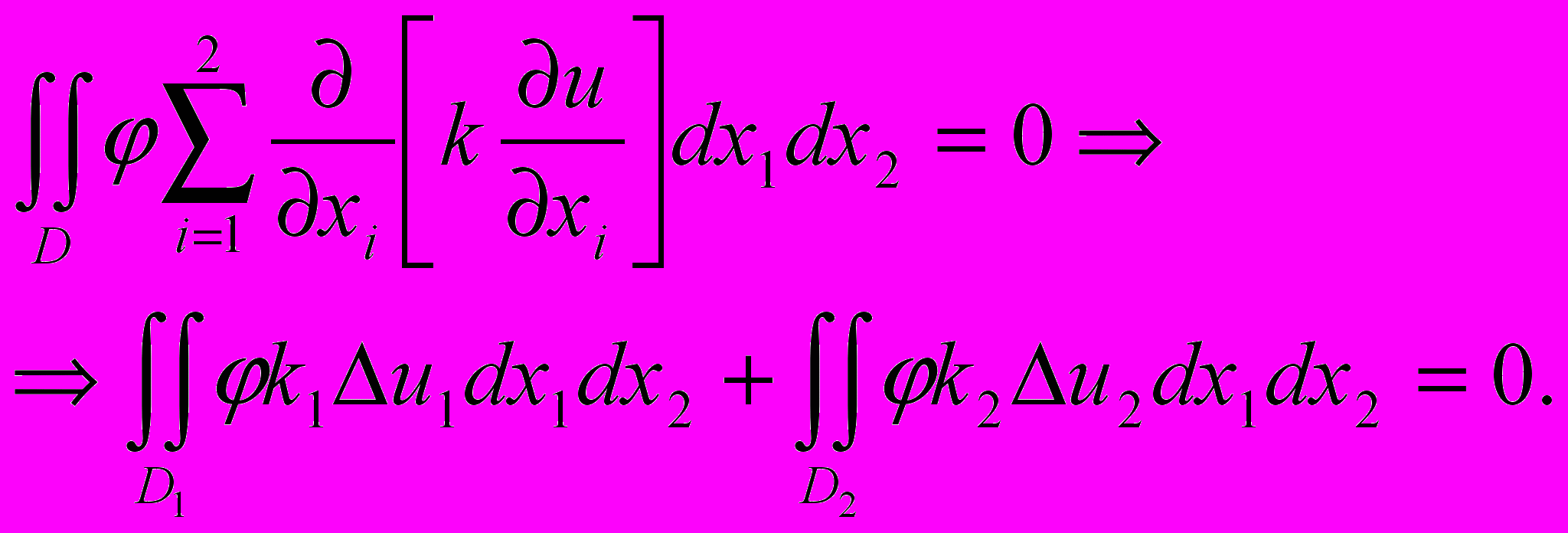
Применим формулу Грина со страницы 2:
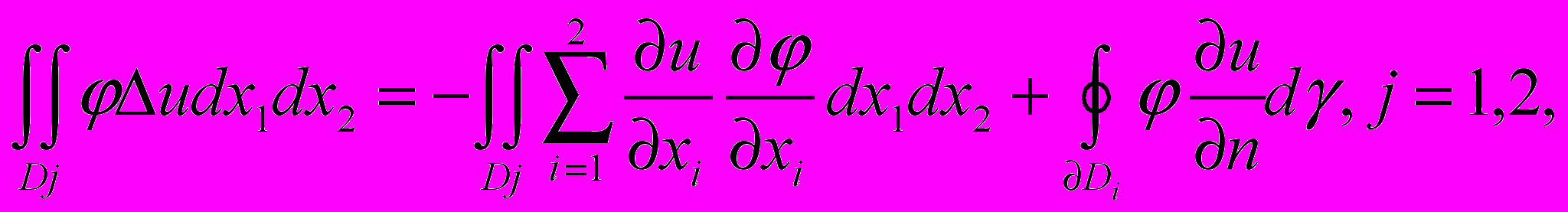 получим
получим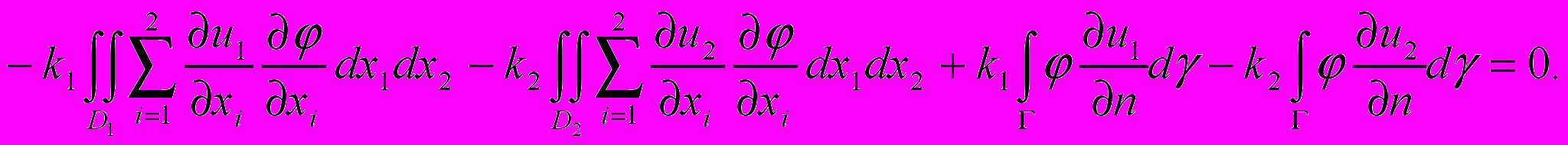
Применим условие теплового баланса на и получим интегральное тождество
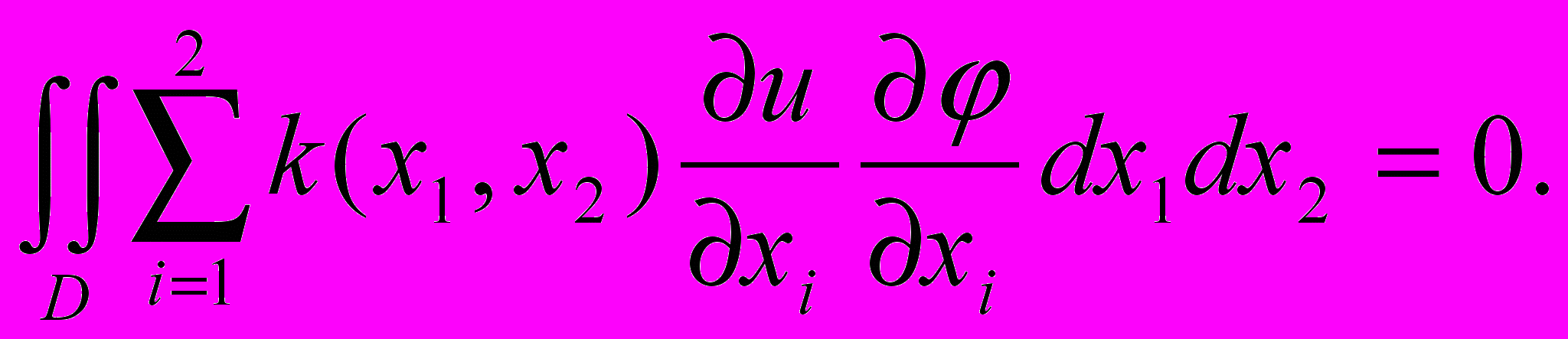
Для его выполнения не требуется существования у коэффициента теплопроводности
к (x1, x2) производных, а функция u(x1, x2) может иметь только производные первого порядка.
Итак, в рассмотренной задаче температура u(x1, x2) не является классическим решением дифференциального уравнения второго порядка, но эта функция удовлетворяет интегральному тождеству. Назовём u(x1, x2) слабым решением уравнения /5/.
Само уравнение /5/ при этом является лишь символической записью.
Чтобы строго определить слабое решение уравнения /3/ , а затем обобщенное решение задачи Дирихле для уравнения /3/, надо описать класс функций u(x1, x2), в котором мы будем определять эти решения.
Пространства функций
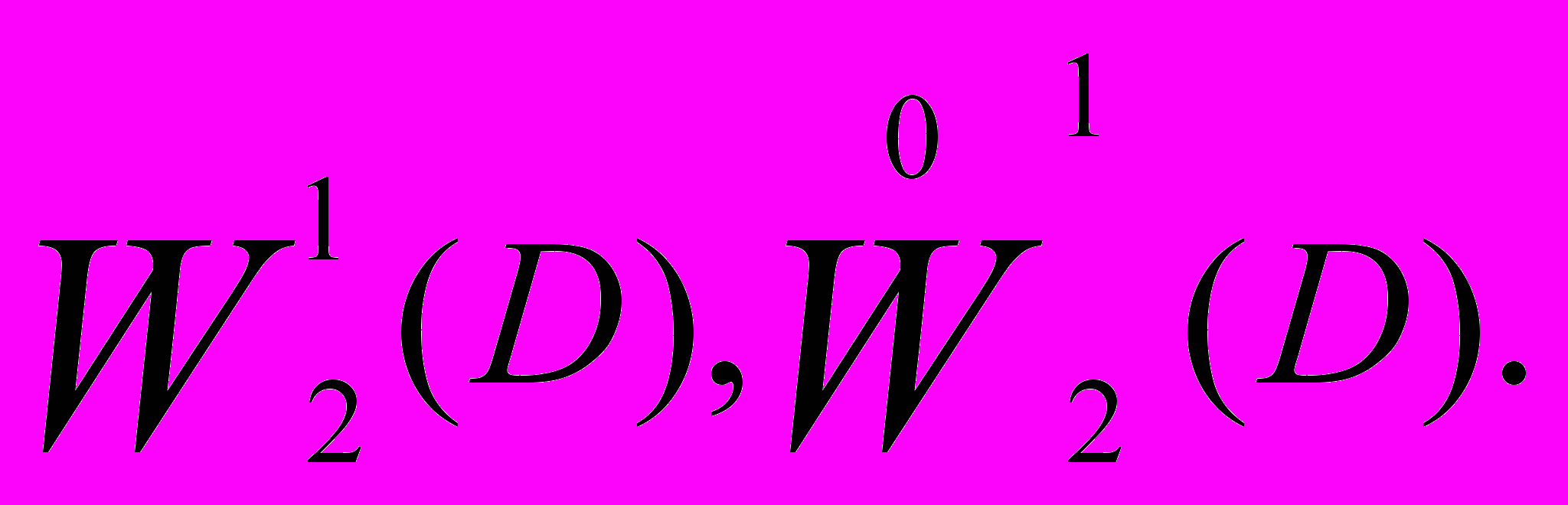
Понятие слабого решения дифференциального
уравнения. Обобщенное решение краевой задачи.
Обозначим x=(x1, x2).
Введем пространство функций
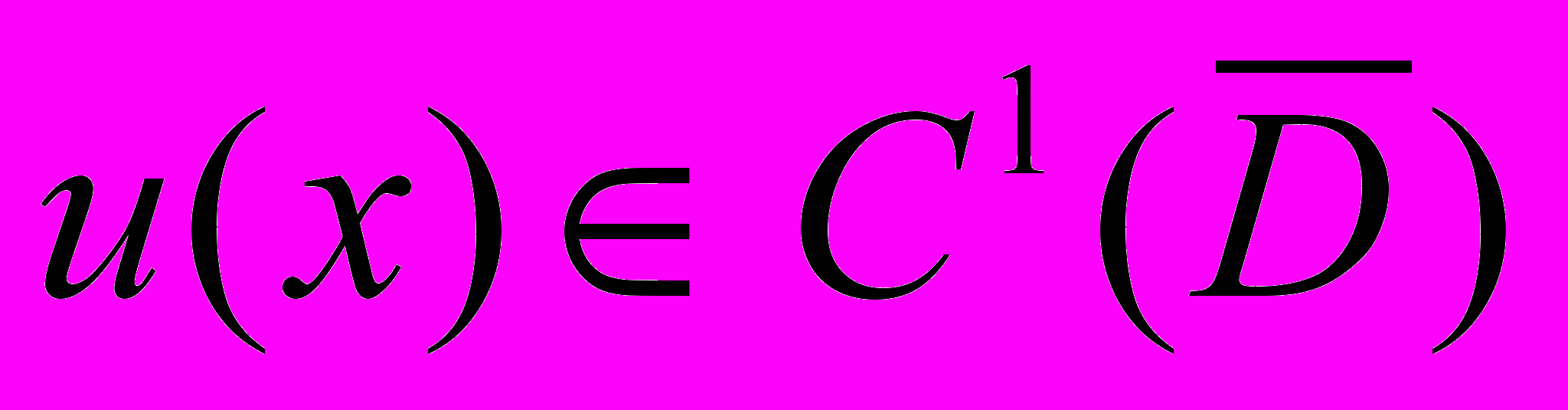 .
.Функция (x) принадлежит пространству C1(
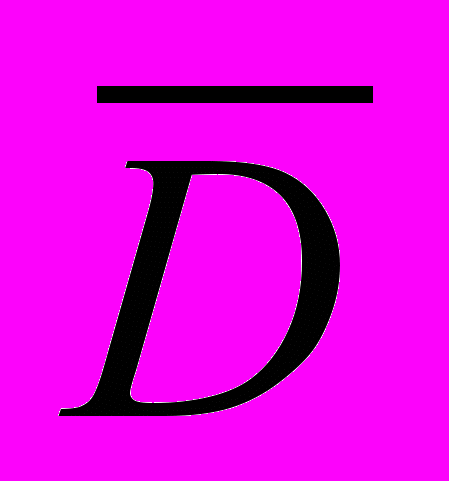 ), если в
), если в области
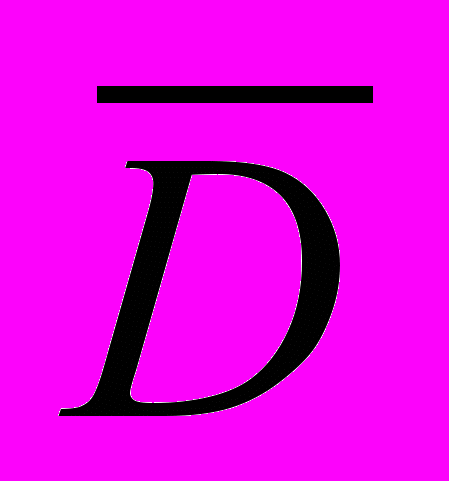 (x) непрерывна и имеет непрерывные частные
(x) непрерывна и имеет непрерывные частные производные первого порядка.
Обозначим
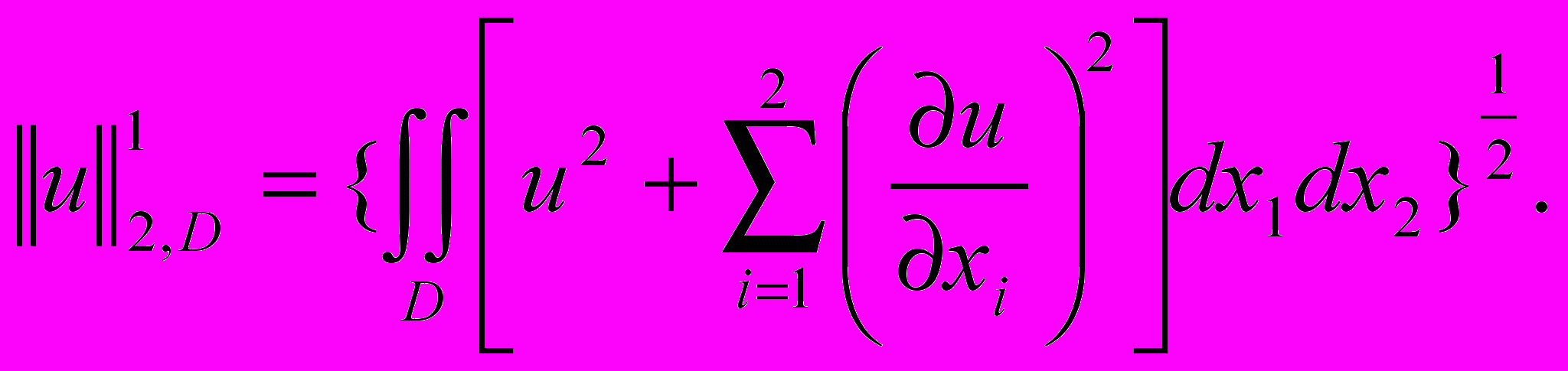
 называется нормой функции u(x) в пространстве функций
называется нормой функции u(x) в пространстве функций 
Рассмотрим в
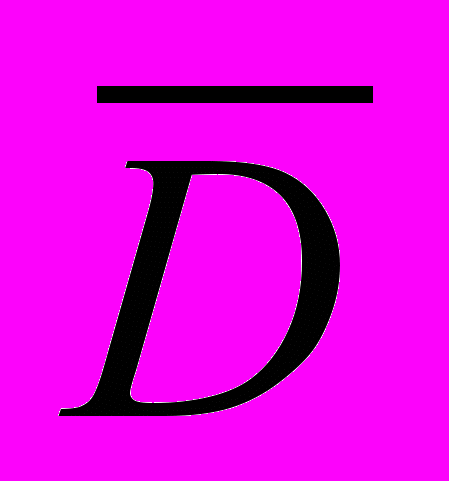 множество бесконечно
множество бесконечно дифференцируемых функций, обозначим это множество
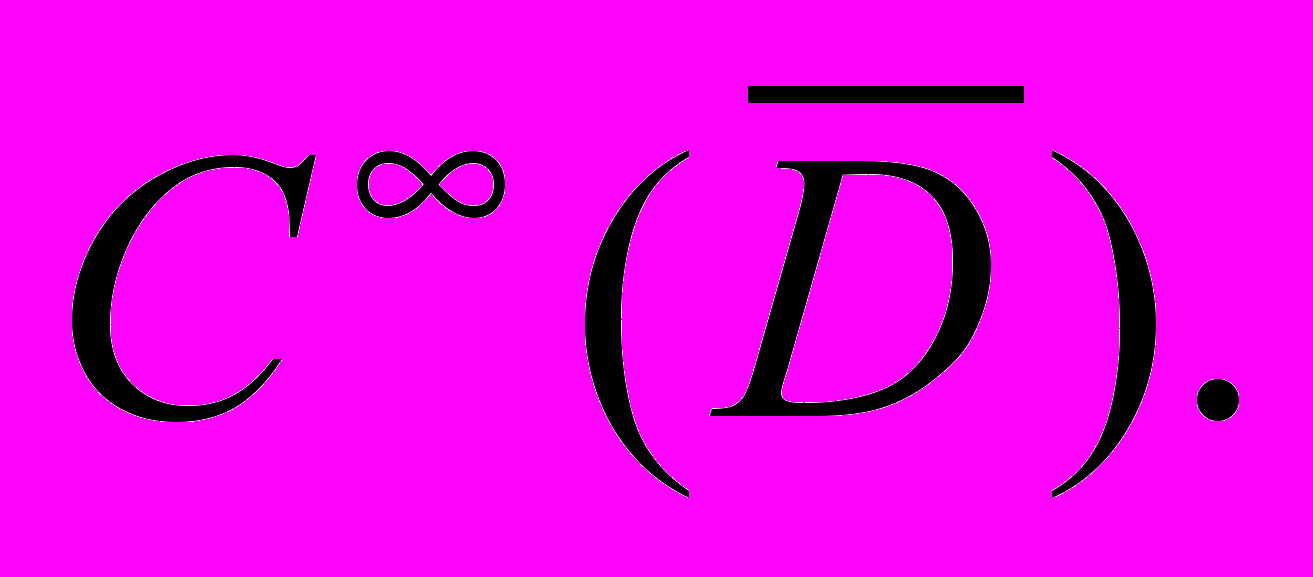
Рассмотрим множество функций v(x), каждая из которых
является предельной для последовательности {un} функ-
ций
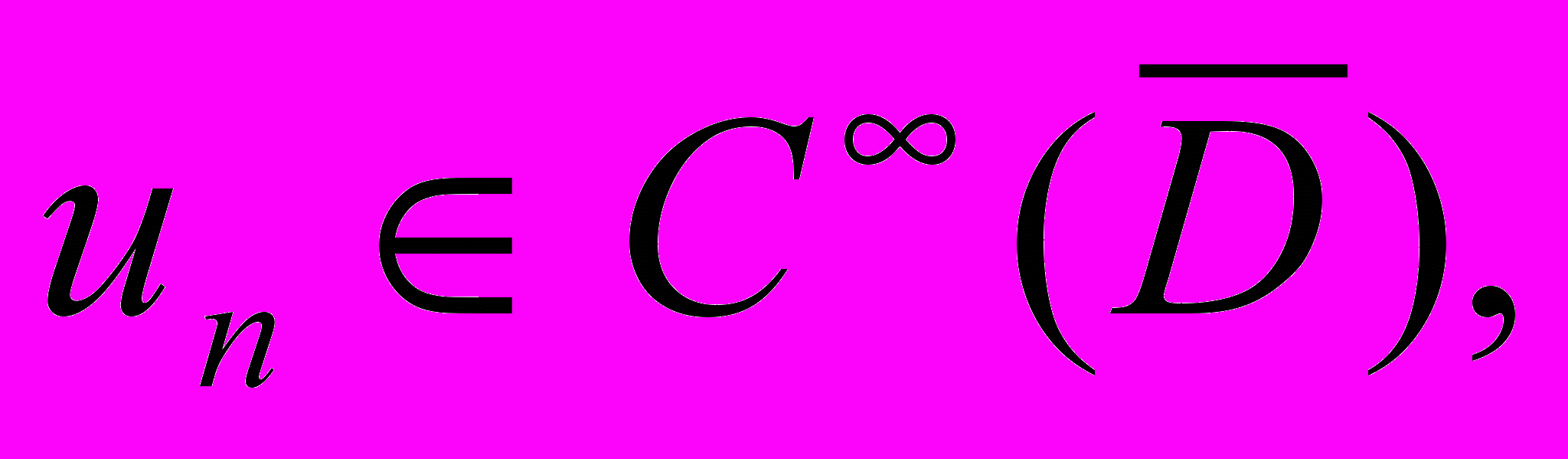 причем предел понимается в том смысле,
причем предел понимается в том смысле,что
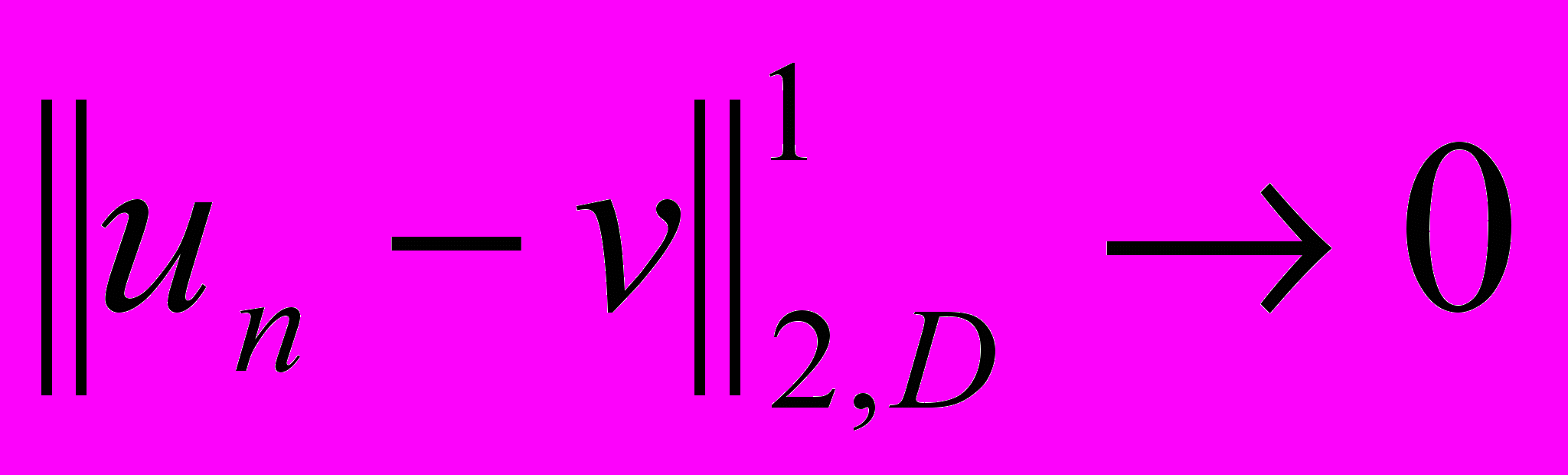 при
при  (сильная сходимость в
(сильная сходимость в 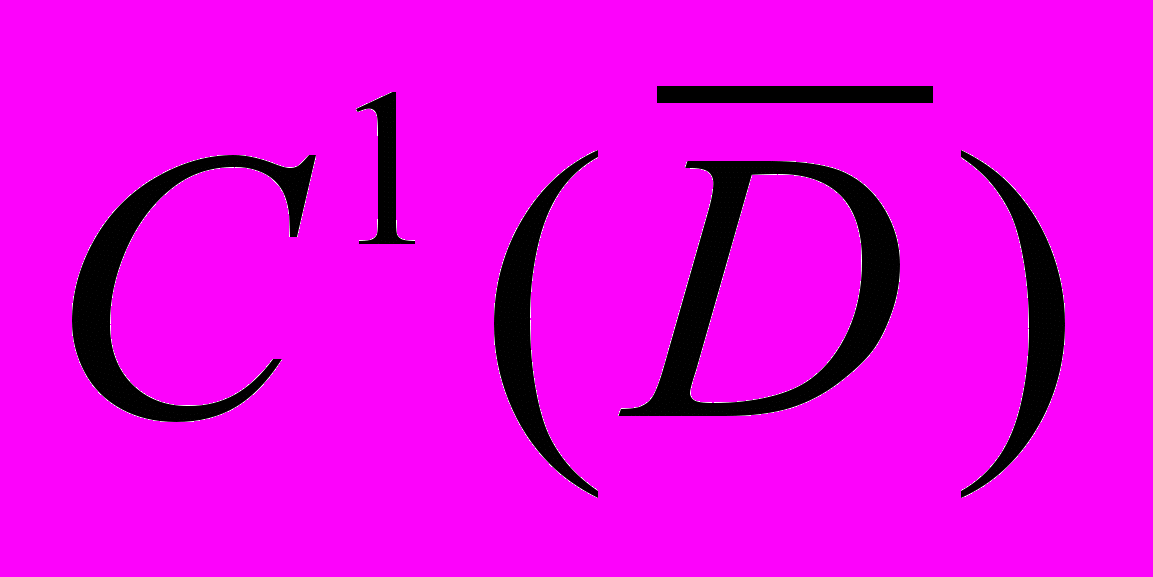 ). Присоединим к множеству функций
). Присоединим к множеству функций 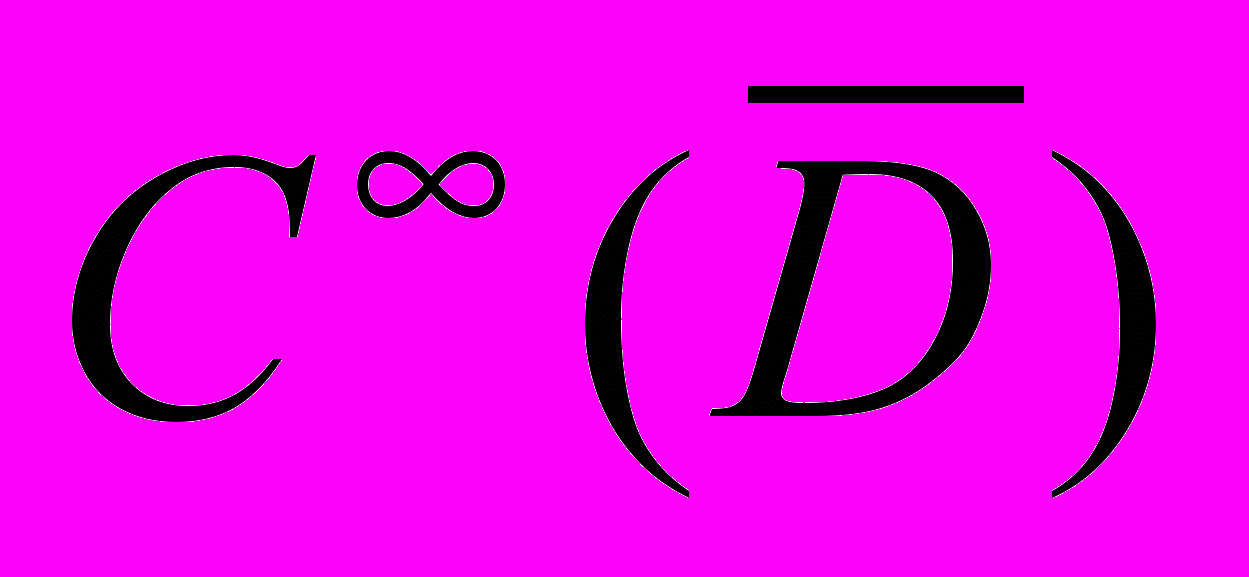 множество функций v(x). Полученное множество
множество функций v(x). Полученное множество называется замыканием пространства
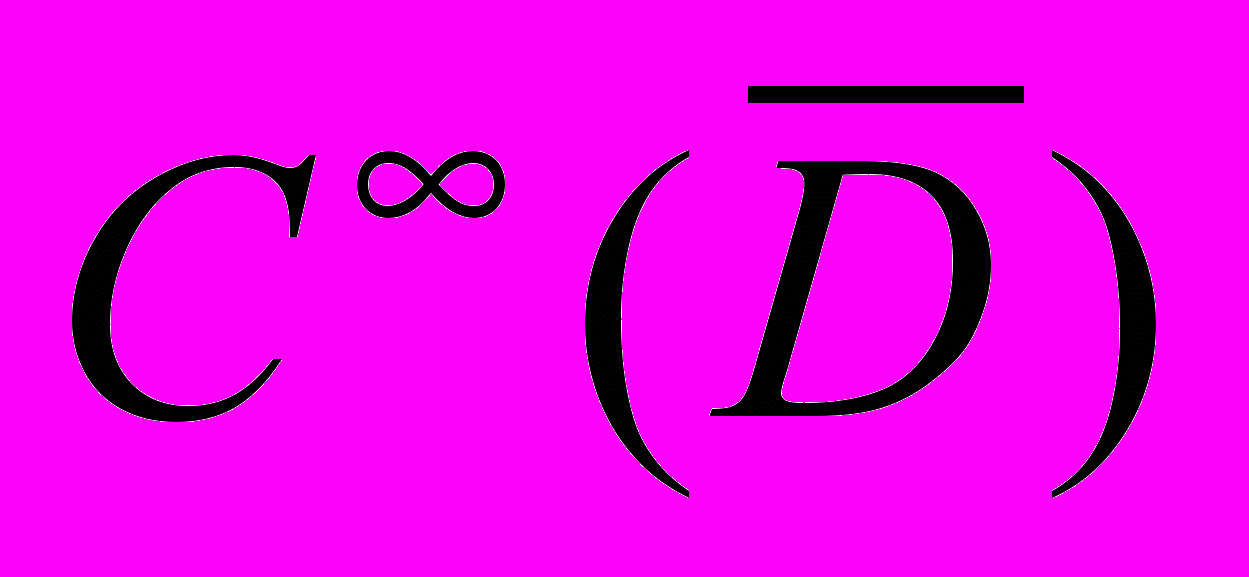 по указанной
по указанной норме; это замыкание назовем соболевским пространством

(или пространством Соболева).
Теперь рассмотрим в D множество бесконечно
дифференцируемых функций, обращающихся в нуль в
некоторой окрестности границы D. Обозначим это
множество
 Пусть {vn}- бесконечная
Пусть {vn}- бесконечная последовательность функций из
 Рассмотрим
Рассмотрим функцию v(x), для которой
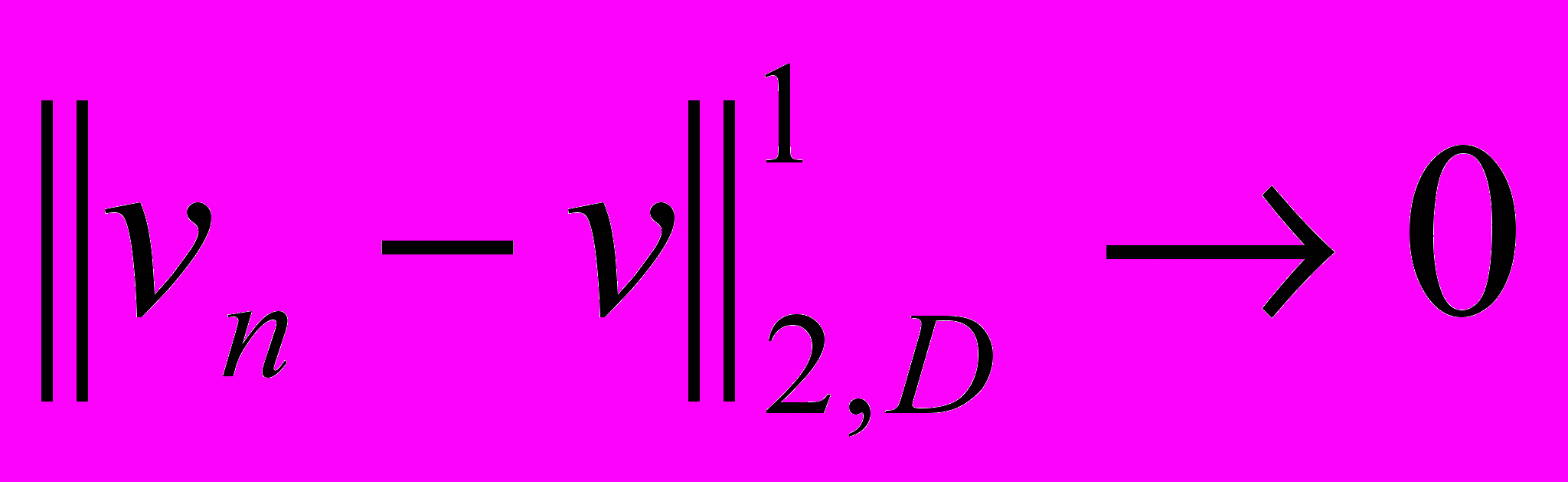 при
при 
Замкнем пространство
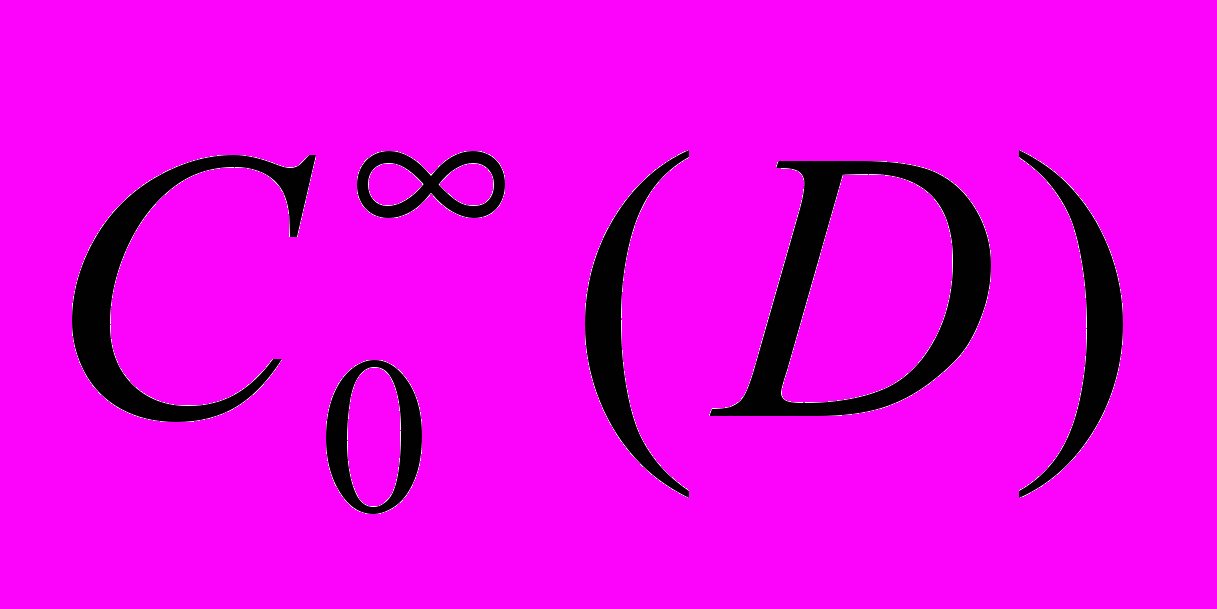 по рассматриваемой норме
по рассматриваемой нормеуказанным выше способом. Полученное пространство
обозначим
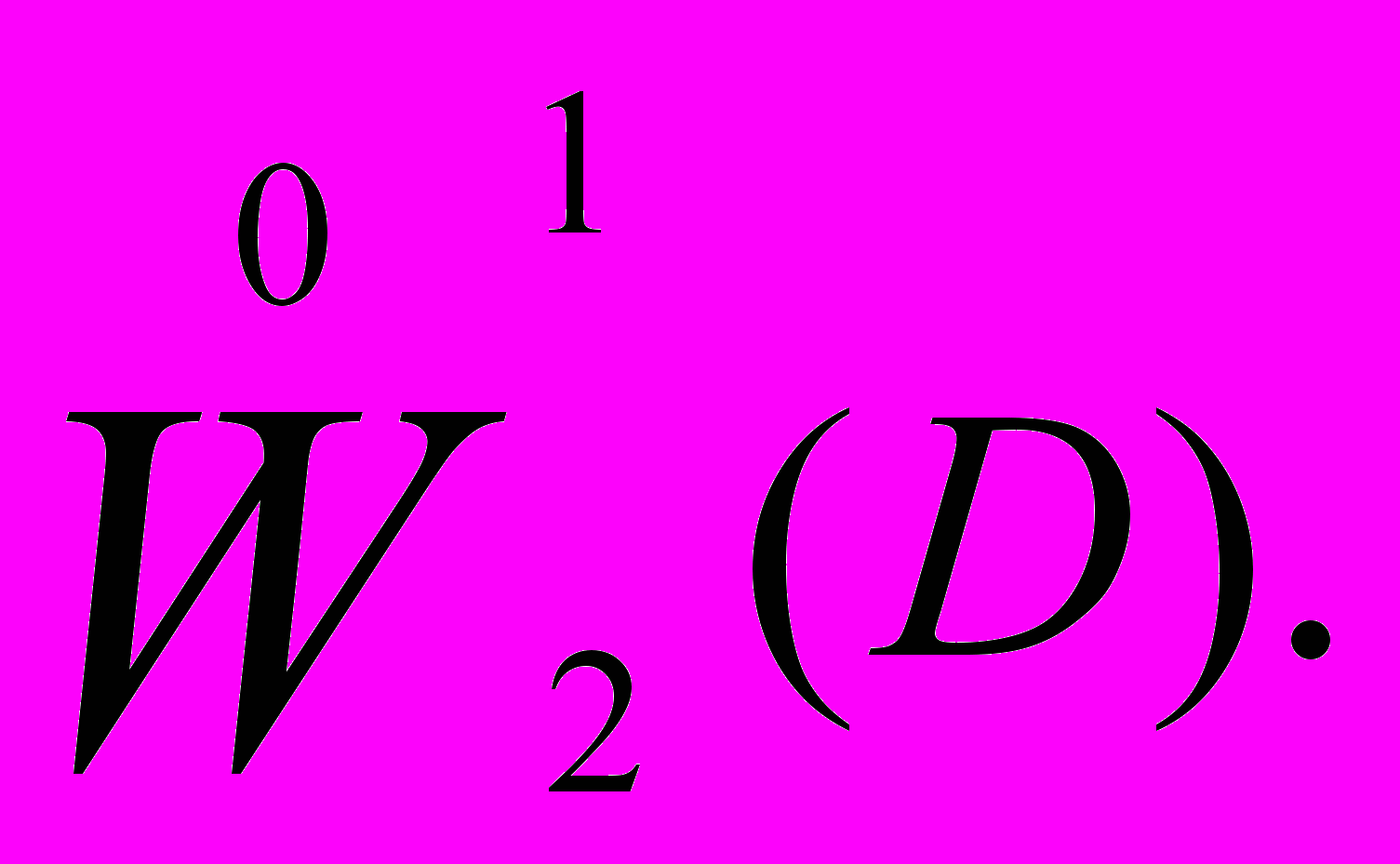
Имеет место вложение

 .
.Рассмотрим в области D дифференциальное уравнение второго
порядка /3/ со стр.2
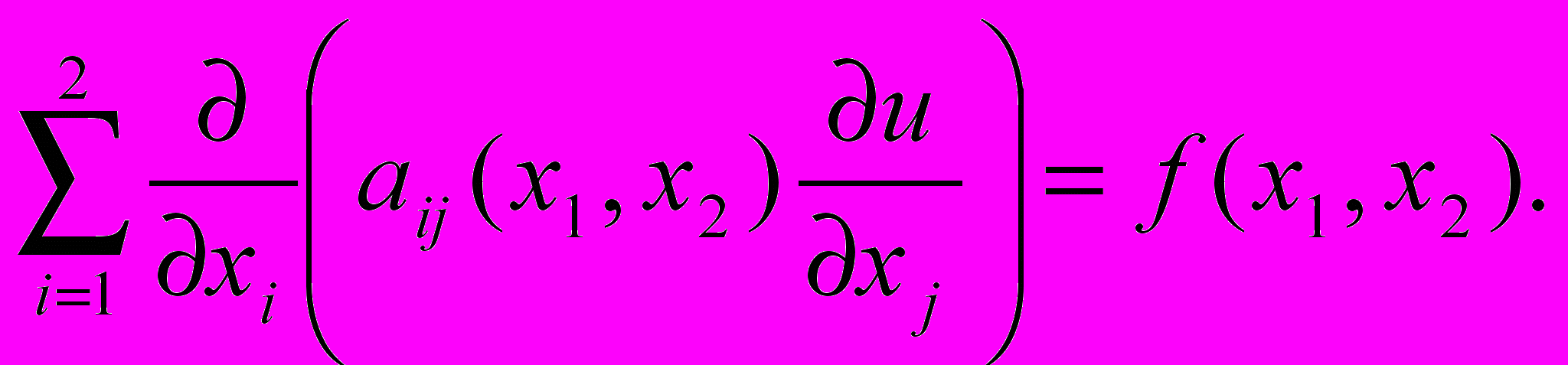
Тождество /4/ со стр.3 положим в основу определения слабого решения уравнения /3/:

если функция (x)
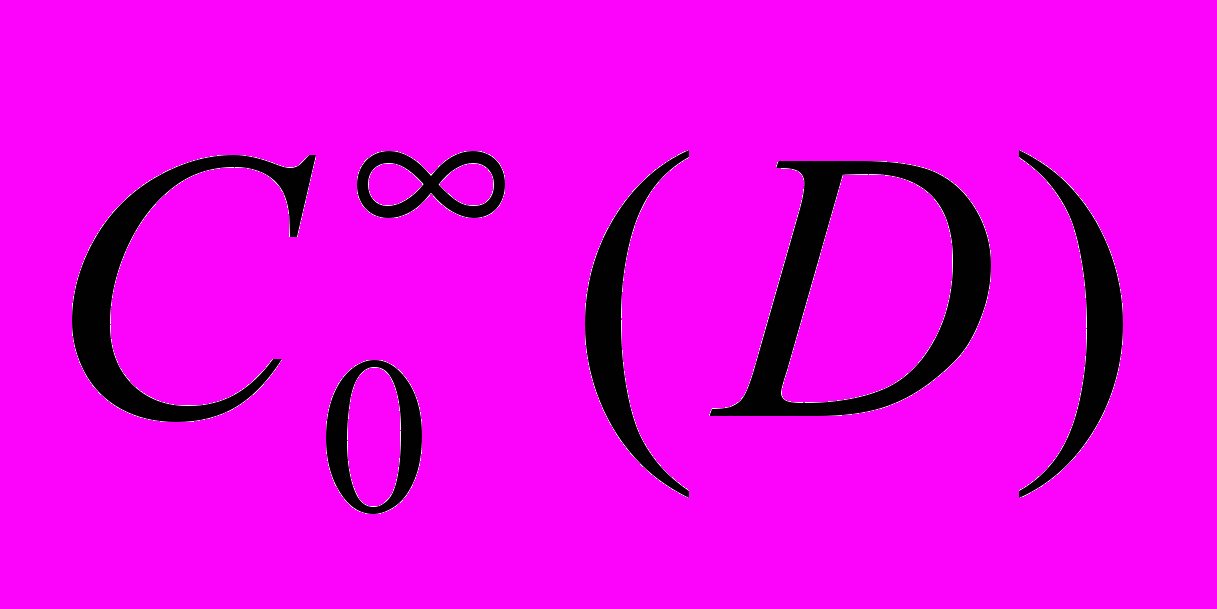
Слабым решением эллиптического уравнения /3/ в
области D называется функция u(x) из пространства
 удовлетворяющая интегральному тождеству /4/
удовлетворяющая интегральному тождеству /4/при любой функции

Обобщенным решением первой краевой задачи
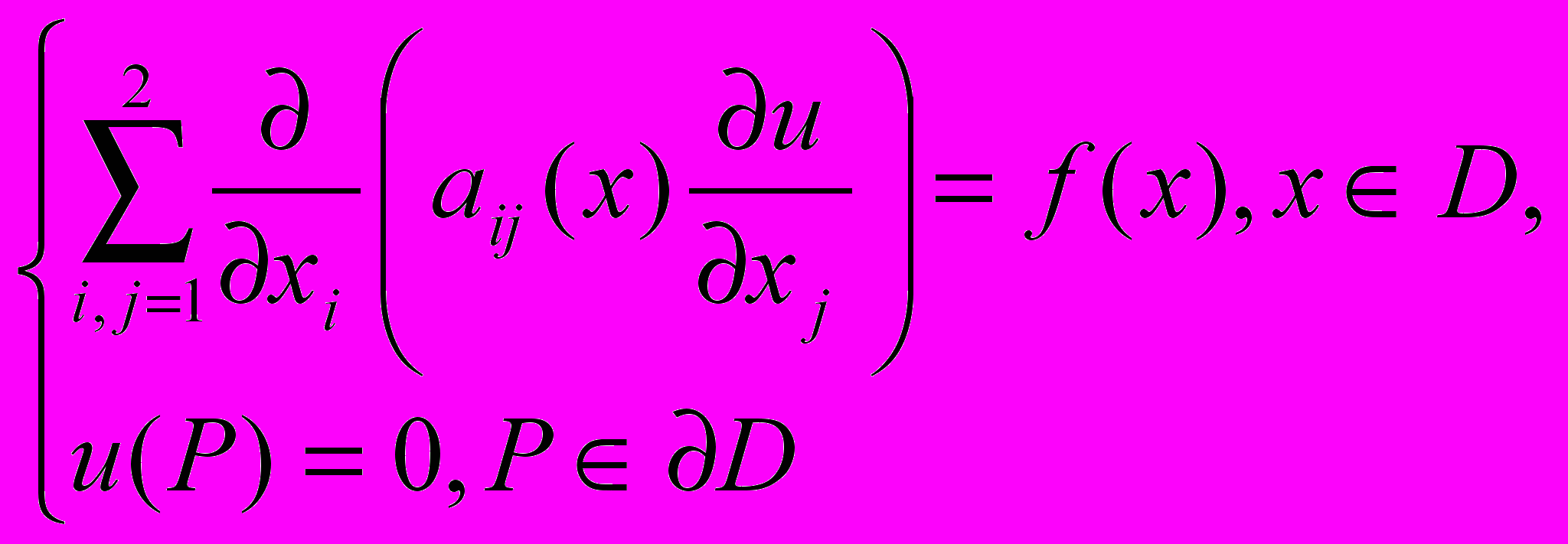
для эллиптического уравнения /3/ называется слабое
решение этого уравнения, принадлежащее пространству
функций
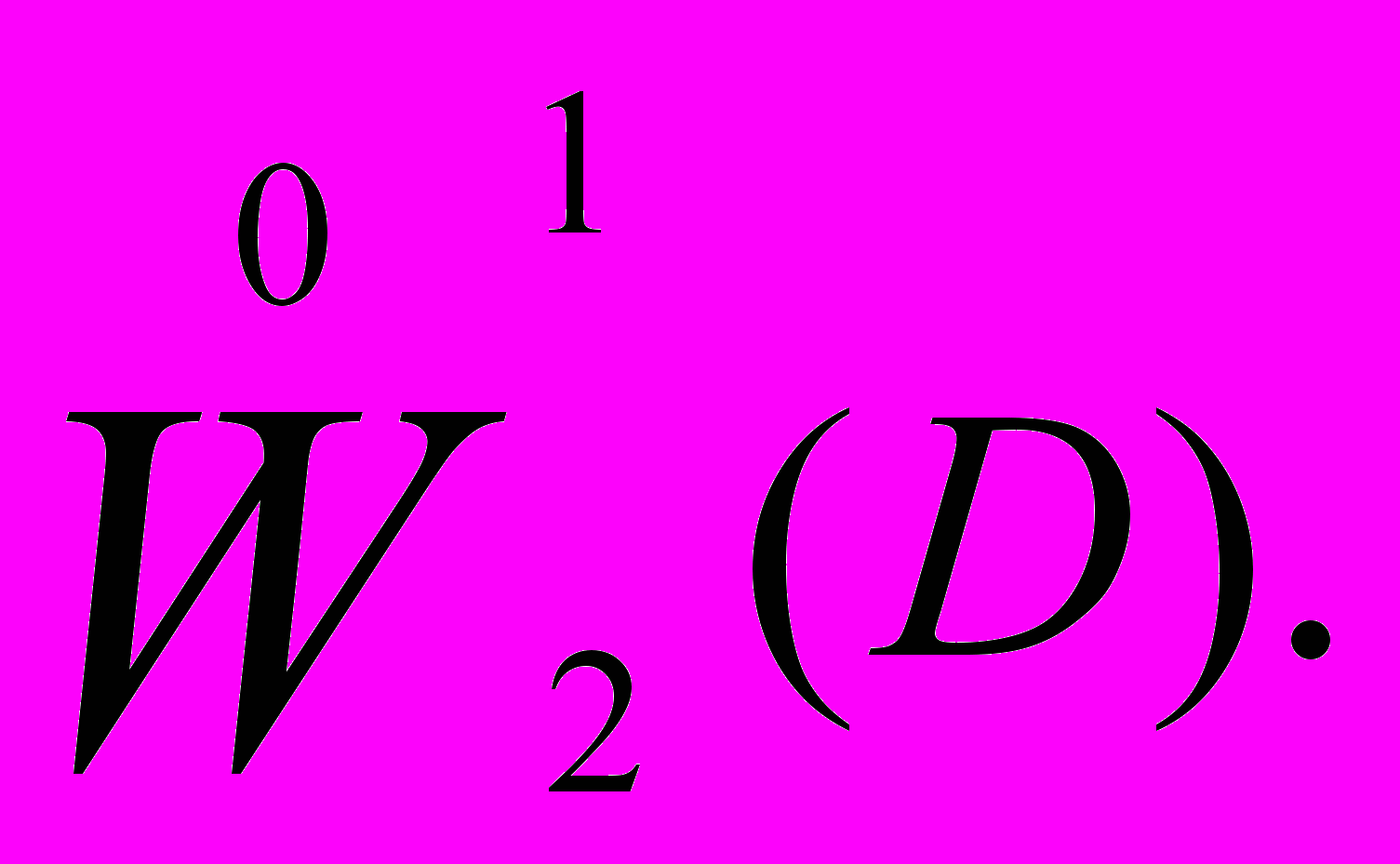
Помимо литературы, указанной в теме1, см.
Соболев С.Л. Уравнения математической физики. М., Наука, 1966.
Соболев С.Л. Некоторые применения функционального анализа в математической физике.
Сибирское отделение АН СССР, 1962.
Ландис Е.М. Уравнения второго порядка эллиптического и параболического типов. М., Наука, 1971.
Грин Джордж(1793-1841)- английский математик. В 1828г. выпустил труд «Опыты применения математического анализа к теориям электричества и магнетизма», положив начало методам, которые мы теперь относим к разделу математической физики. Наряду с немецким ученым Карлом Фридрихом Гауссом создал основы теории потенциала. Именно Грином впервые применен сам термин «потенциал». Он учился сначала самостоятельно, а в 1833г. поступил в Колледж Кембриджского университета. В это время он публикует труды, которые явились развитием и теоретическим применением «Опытов». К числу его лучших работ принадлежит трактат «Об отражении и применении звука».
Соболев Сергей Львович(1908-1989)- русский математик. Один из крупнейших математиков XX века, внесший основополагающий вклад в современную науку.
После окончания Ленинградского университета С. Л. Соболев начал заниматься геофизикой в Сейсмическом институте. Вместе с академиком В. И. Смирновым он открыл новую область в математической физике, позволяющую решить ряд сложнейших задач, связанных с волновыми процессами в сейсмологии. В дальнейшем метод Смирнова-Соболева нашёл широкое применение в геофизике и математической физике.
С 1934 года С. Л. Соболев заведовал отделом дифференциальных уравнений с частными производными в Математическом институте им. В. А. Стеклова АН СССР. В 30-х годах С. Л. Соболев получил ряд важных результатов по аналитическим
решениям систем дифференциальных уравнений в частных производных ,интегро-дифференциальных уравнений со многими независимыми переменными, предложил новые методы решения задачи Коши для уравнений в частных производных второго порядка.
В 1933 году С. Л. Соболев был избран членом-корреспондентом, а в 1939 году — действительным членом АН СССР по Отделению математических и естественных наук (математика). В 1940-х годах С. Л. Соболев развивал направление функционального анализа и вычислительной математики для решения задач математической физики. Им была написана монография «Уравнения математической физики».
Главная книга его жизни- «Некоторые применения функционального анализа в математической физике»,
в которой он подробно изложил теорию пространств
функций с обобщенными производными, вошедшими в
науку как пространства Соболева (Соболевские
пространства).
В 1955 году С. Л. Соболев, будучи профессором МГУ,
выступил инициатором создания Вычислительного центра МГУ, который за короткое время вошёл в число самых
мощных в стране. Вместе с академиками
М. А. Лавреньтьевым и С. А. Христиановичем С. Л. Соболев стал инициатором создания и организатором Сибирского отделения Академии наук СССР, начавшегося со
строительства Новосибирского академгородка.
С 1957 по 1983 гг. С. Л. Соболев возглавлял созданный им Институт математики Сибирского отделения АН СССР (Новосибирск), где появились крупные математические
школы в различных областях математики.
. Награжден многими государственными наградами.
