Geum.ru

Задача Коши для неоднородного уравнения с однородными граничными условиями

Вид материалаЗадача

Содержание


Метод импульсов.
Принцип Дюамеля для дифференциальных уравнений с частными производными
Принцип Дюамеля
Подобный материал:
Тема 6 Решение задачи Коши для линейного неоднородного дифференциального уравнения с частными производными второго порядка. Принцип Дюамеля. | | 2009-02-24


Для того, чтобы разъяснить, что принцип Дюамеля для дифференциальных уравнений с частными производными является обобщением метода вариации произвольных постоянных (МВПП) для линейных обыкновенных дифференциальных уравнений, рассмотрим сначала две задачи для обыкновенных дифференциальных уравнений.

Задача Коши для неоднородного уравнения с однородными граничными условиями

(задача I):




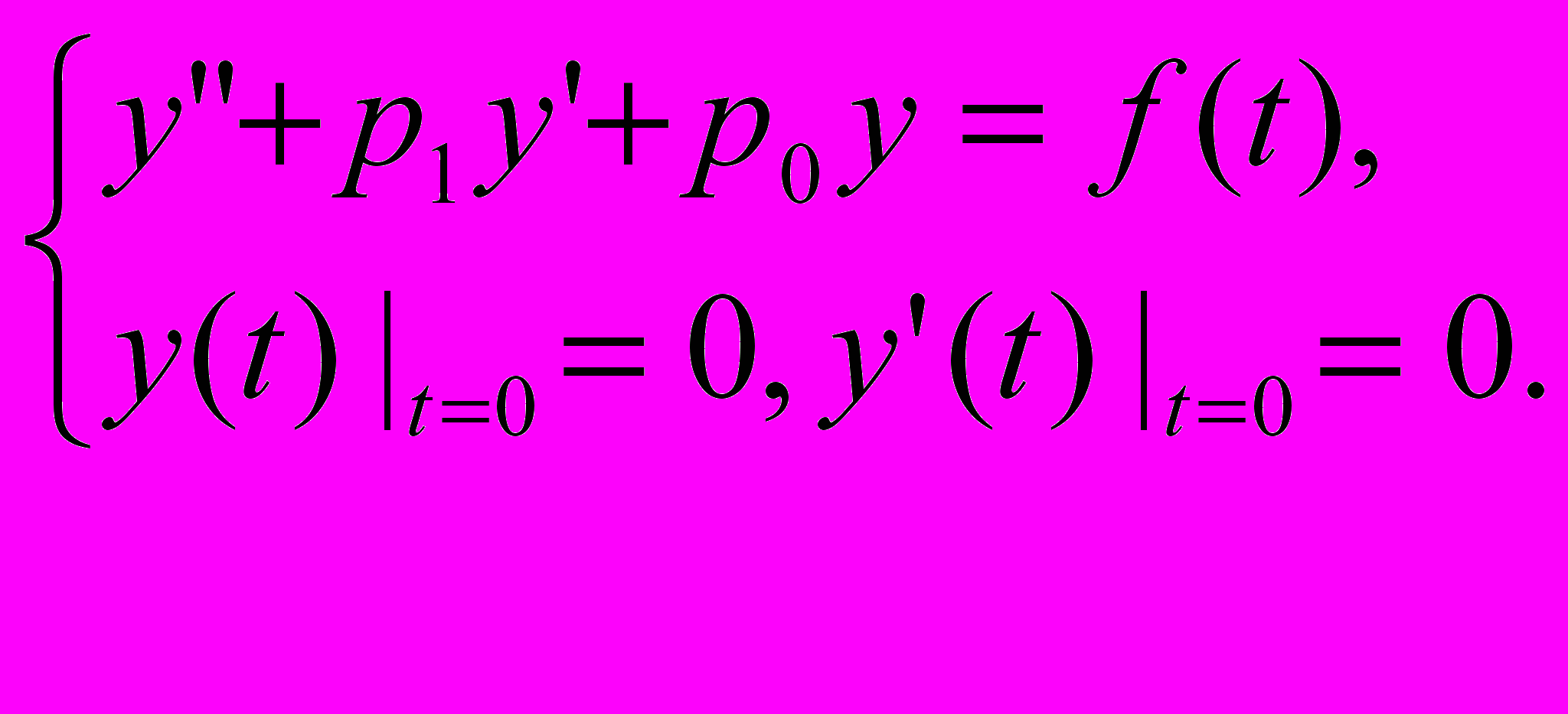
Задача Коши для однородного уравнения с неоднородными начальными условиями (задача II):

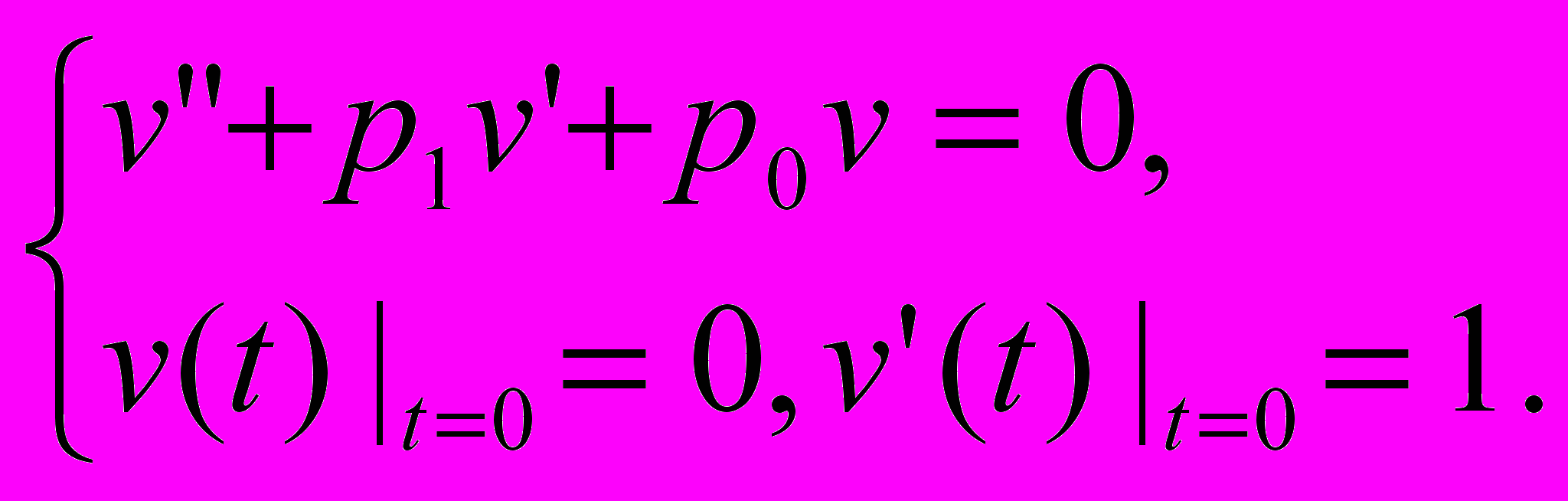
Предполагаем, что коэффициенты p0 и p1 являются постоянными. При решении задачи I мы будем применять знакомый нам МВПП. Мы не только решим задачи I и II, но и укажем на возможный физический смысл функций y(t), v(t), f(t). После чего мы интерпретируем МВПП как метод импульсов. Этот последний метод мы обобщим на случай дифференциальных уравнений с частными производными, что и приведет нас к понятиям принципа Дюамеля и интеграла Дюамеля.

Для простоты ограничимся случаем, когда коэффициенты 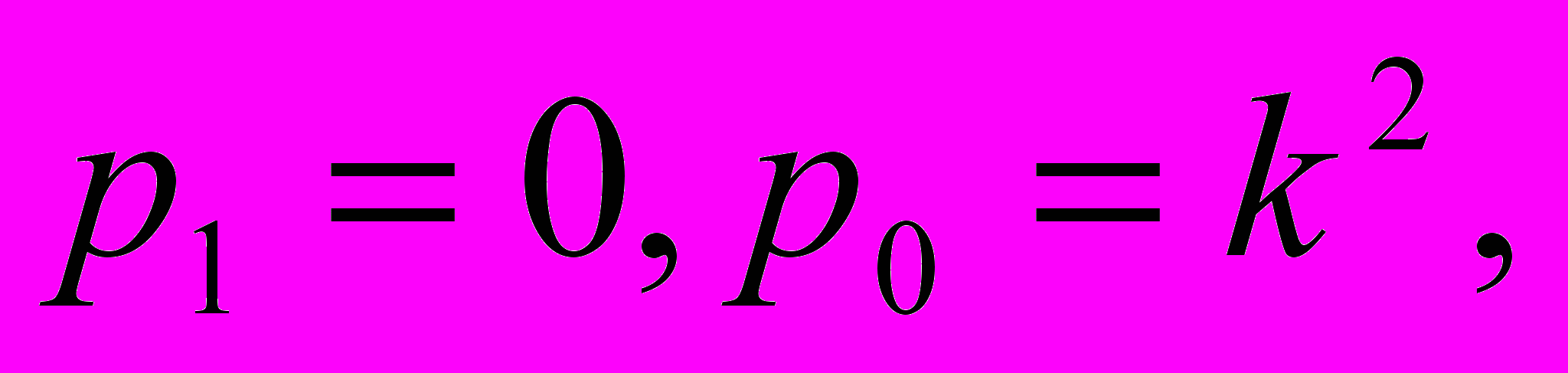k>0, и рассмотрим задачи


(I) 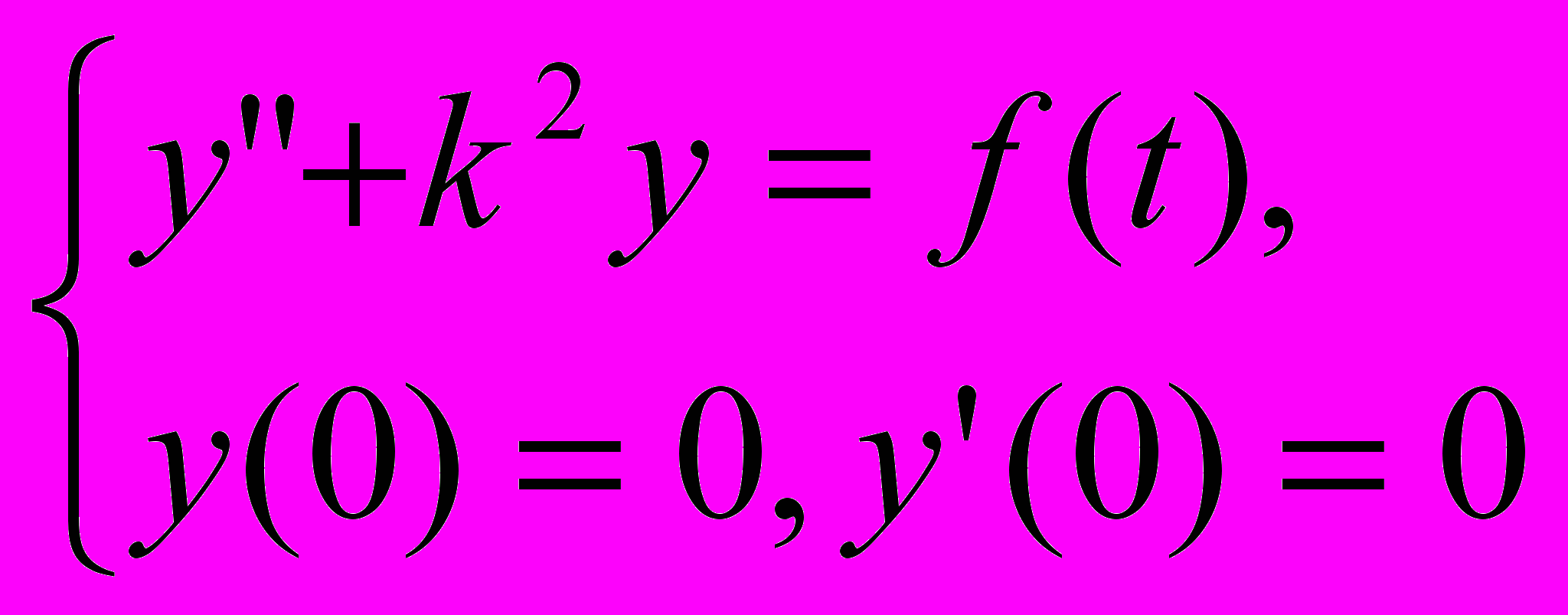и (II)


Сначала решим задачу (II). Характеристическое уравнение для дифференциального уравнения этой задачи имеет вид 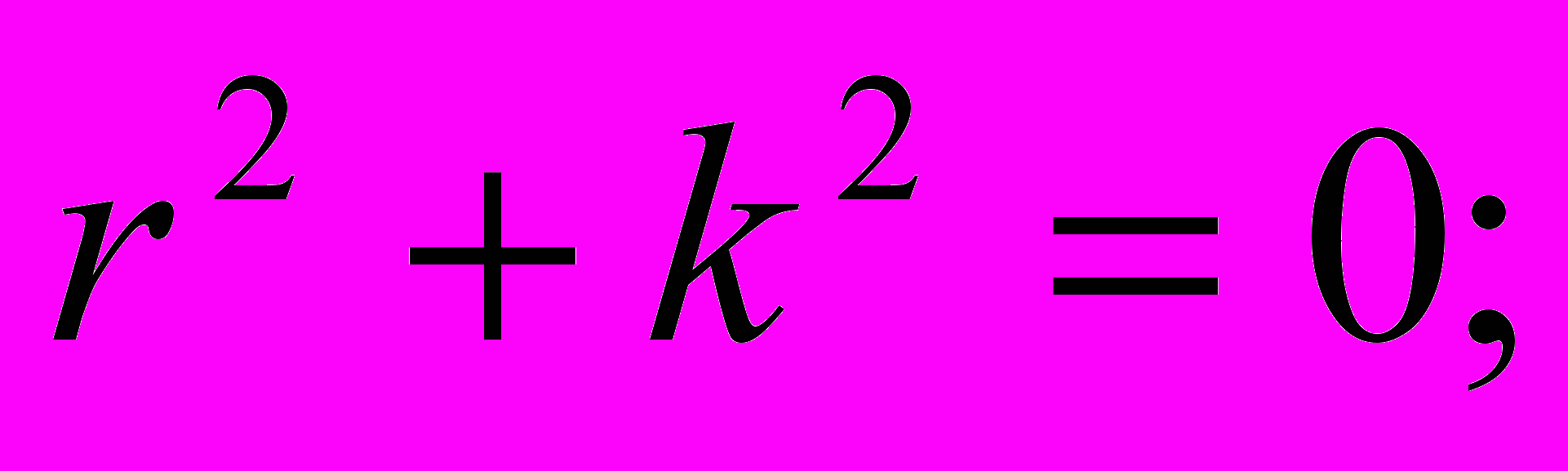его корни 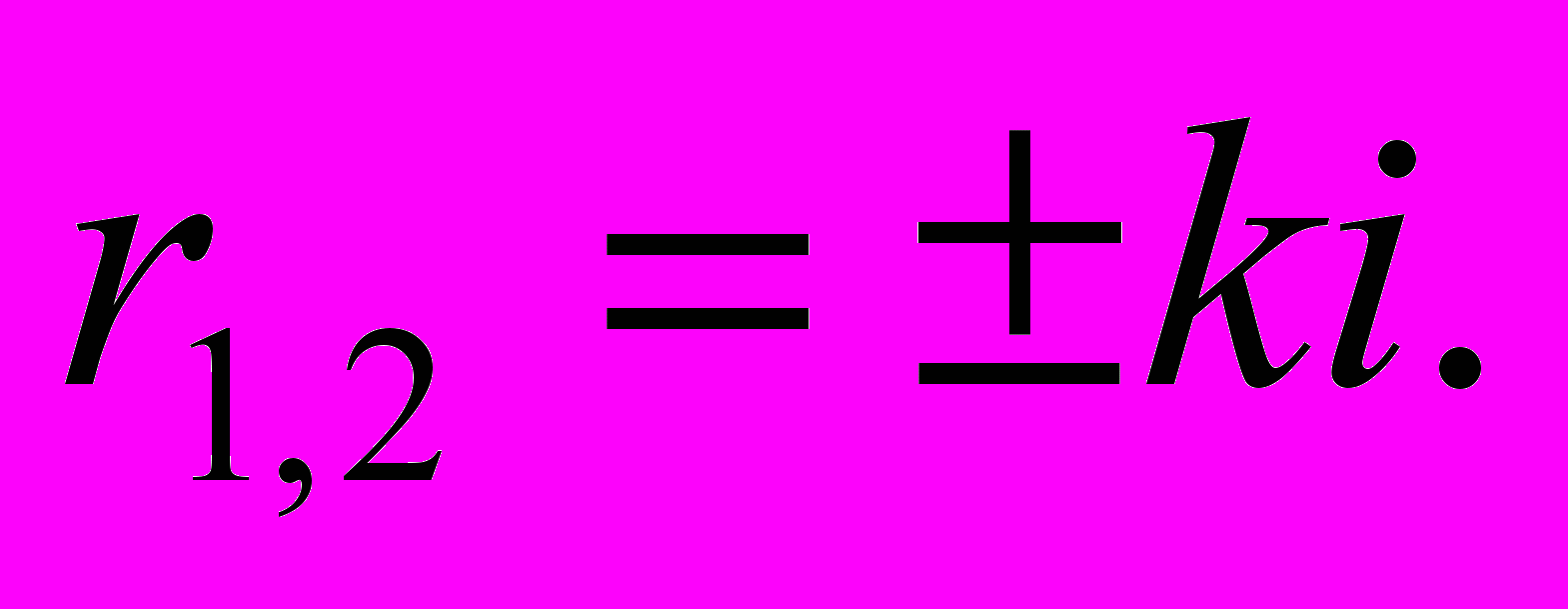Поэтому общее решение дифференциального уравнения- функция 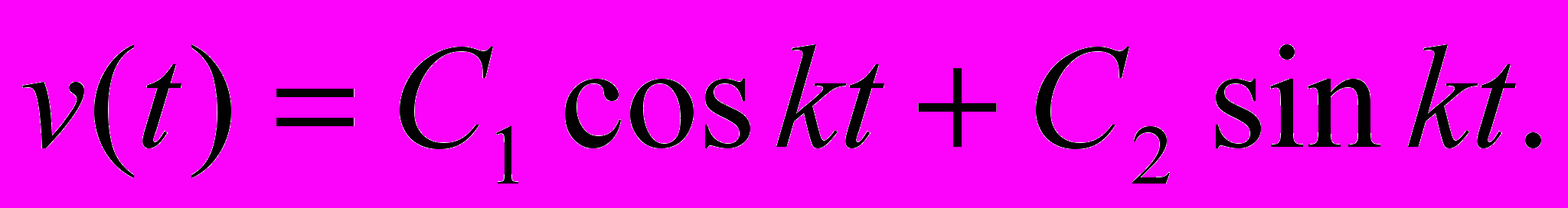А ее производная

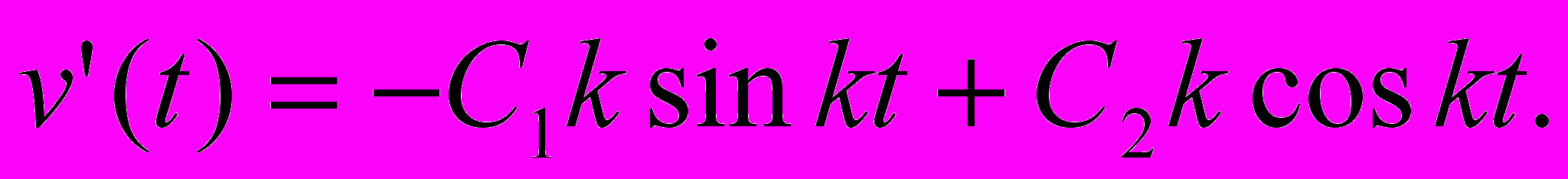Используем начальные условия и получим: С1=0, С2=,

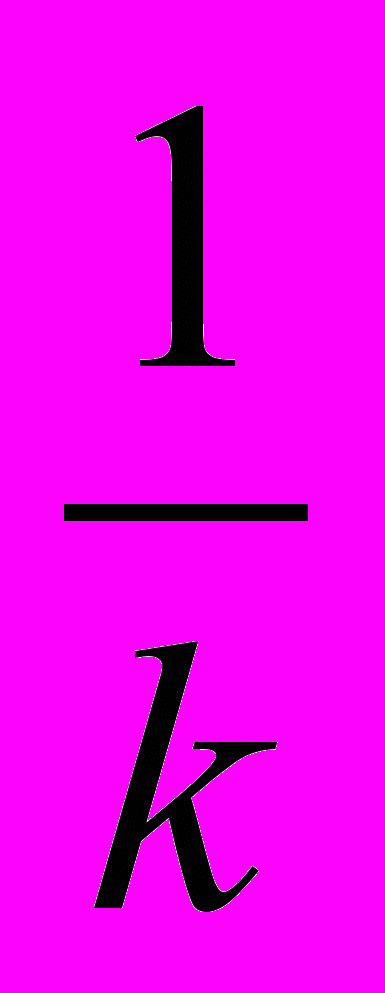так что решение задачи (II)


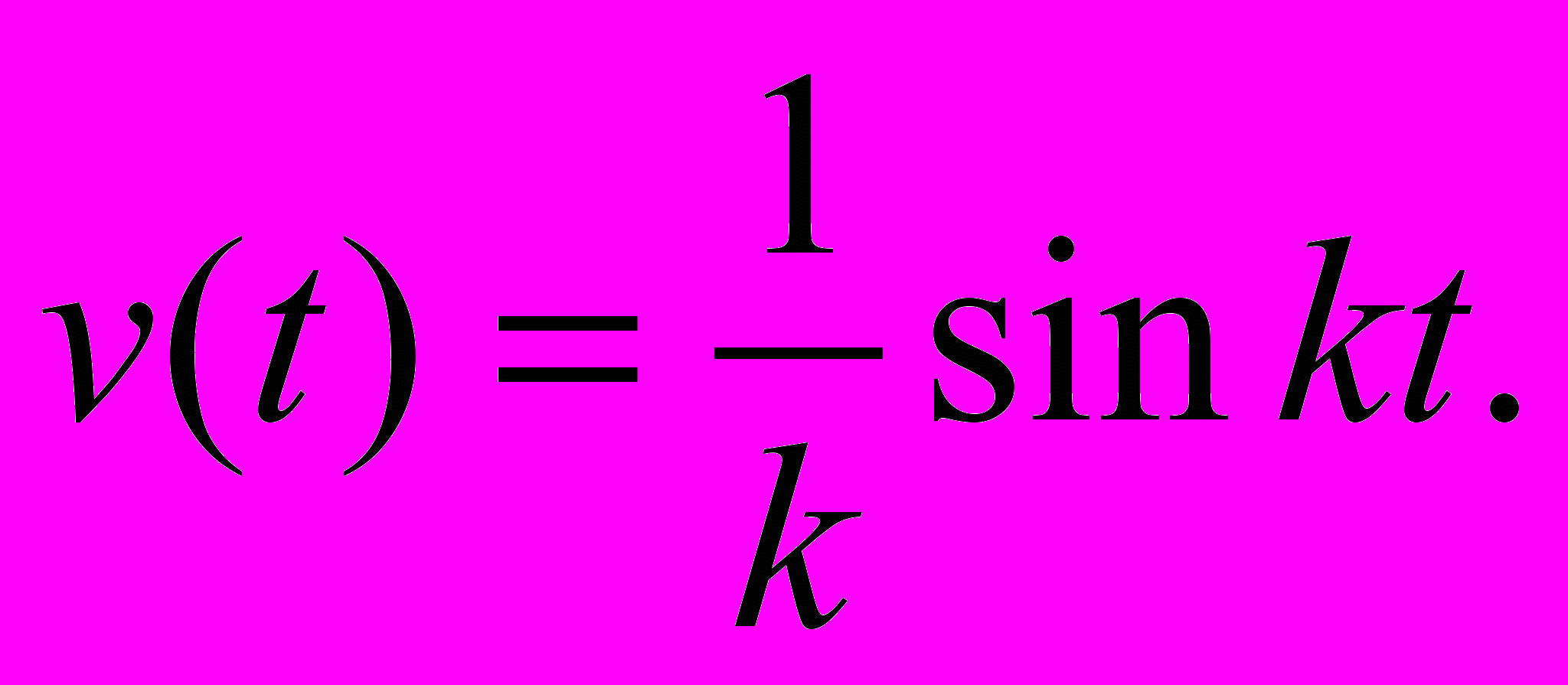
Теперь, используя МВПП, найдем решение y(t) дифференциального уравнения задачи(I):

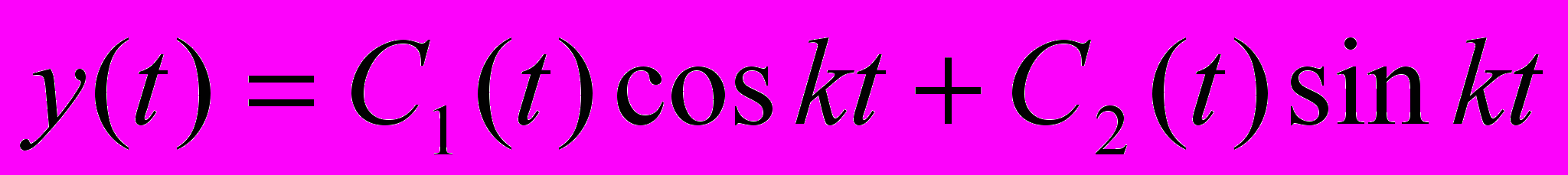. Известно, что при этом производные от функций Сi находятся из решения алгебраической системы



Получаем

Поэтому




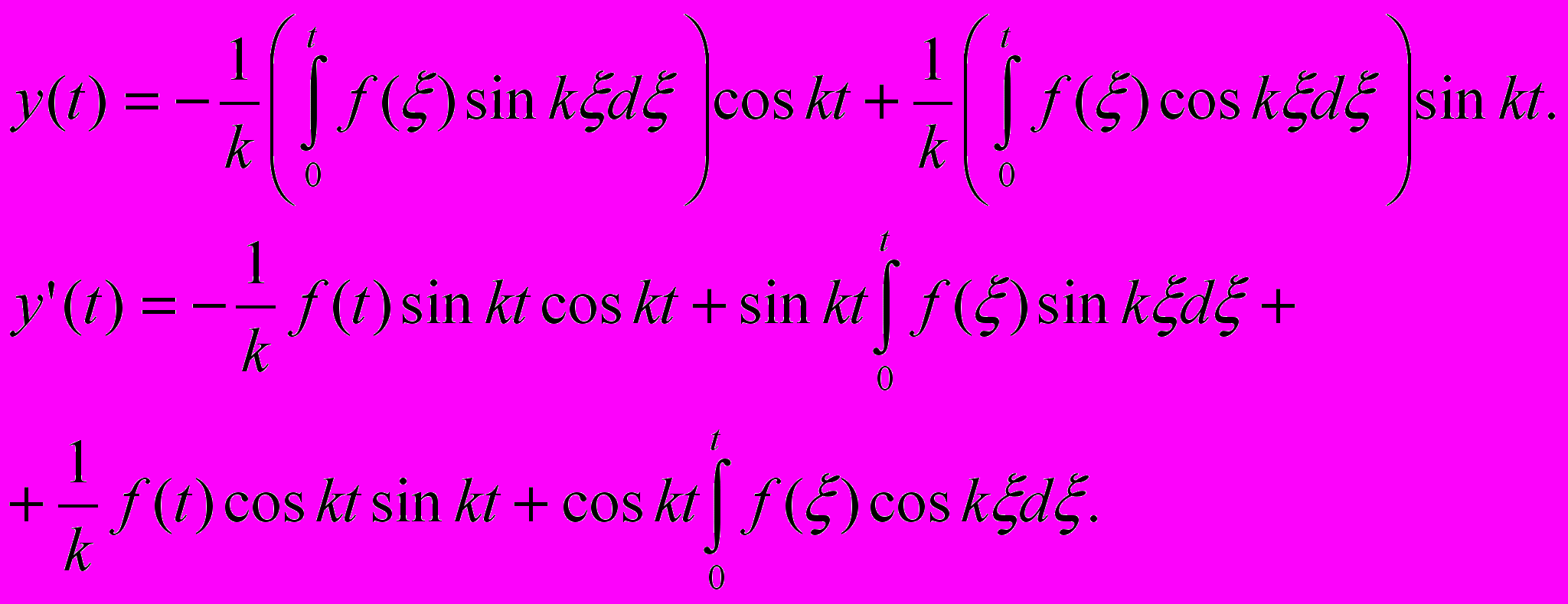
При t=0 y(0)=0. y’(0)=0, т.е. y(t)- решение задачи Коши (I). Запишем y(t) по-другому:

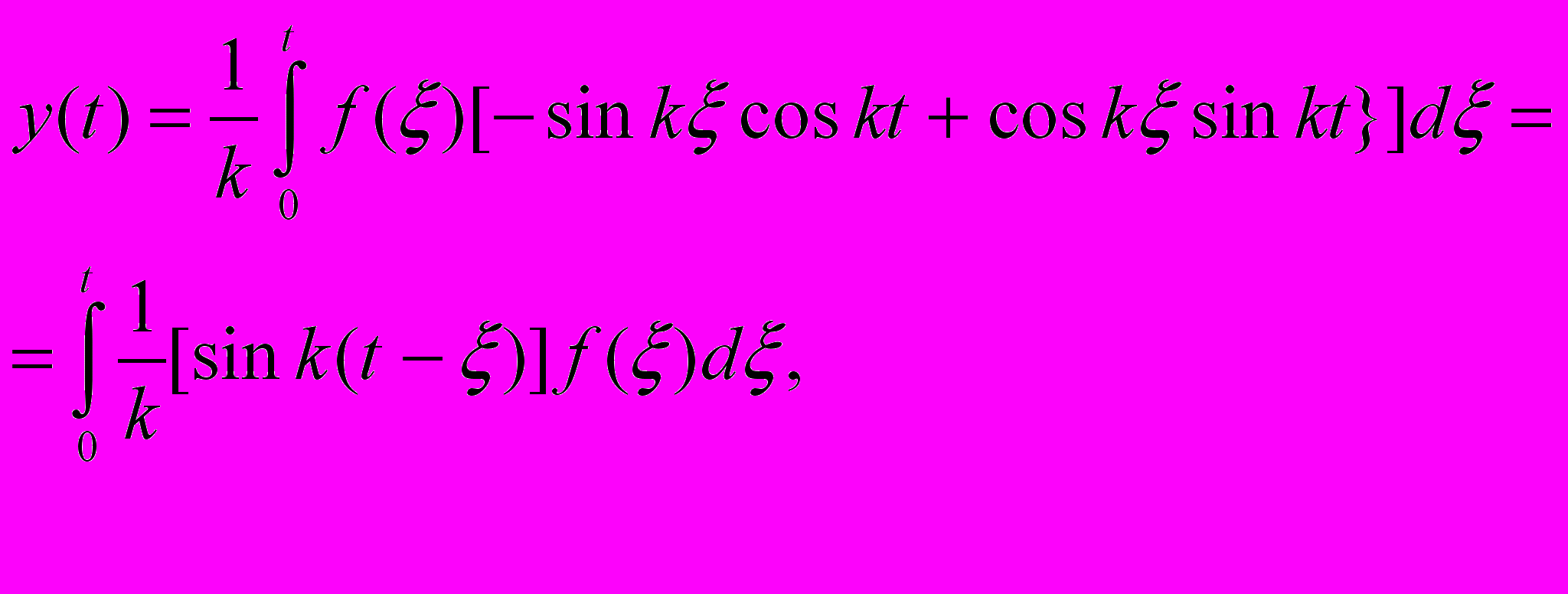так что в подынтегральном выражении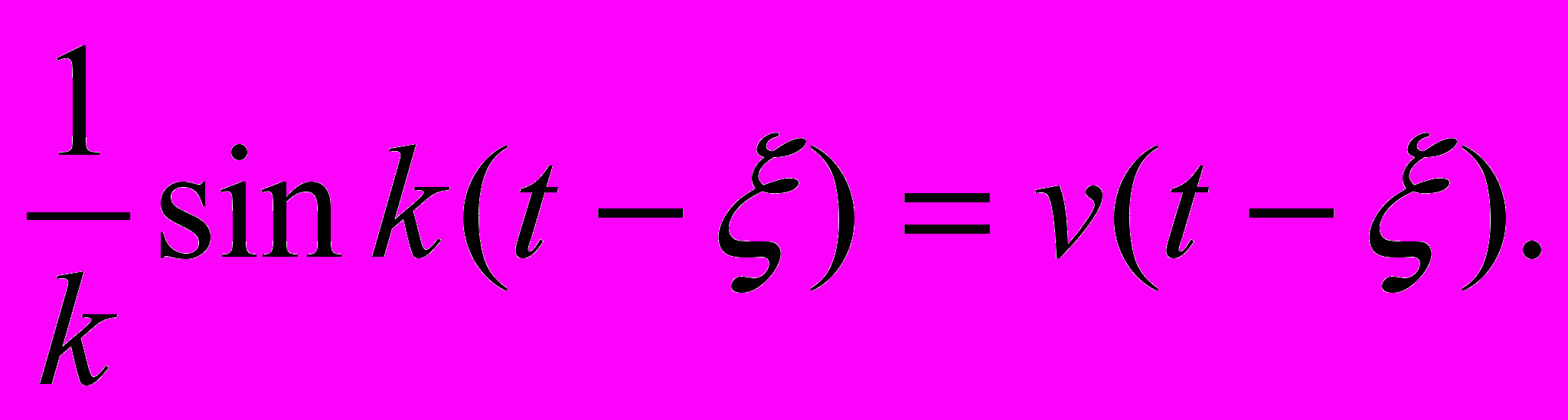



Мы видим, что решение y(t) задачи Коши(I) можно получить, зная решение v(t) задачи Коши (II), по формуле

(*)

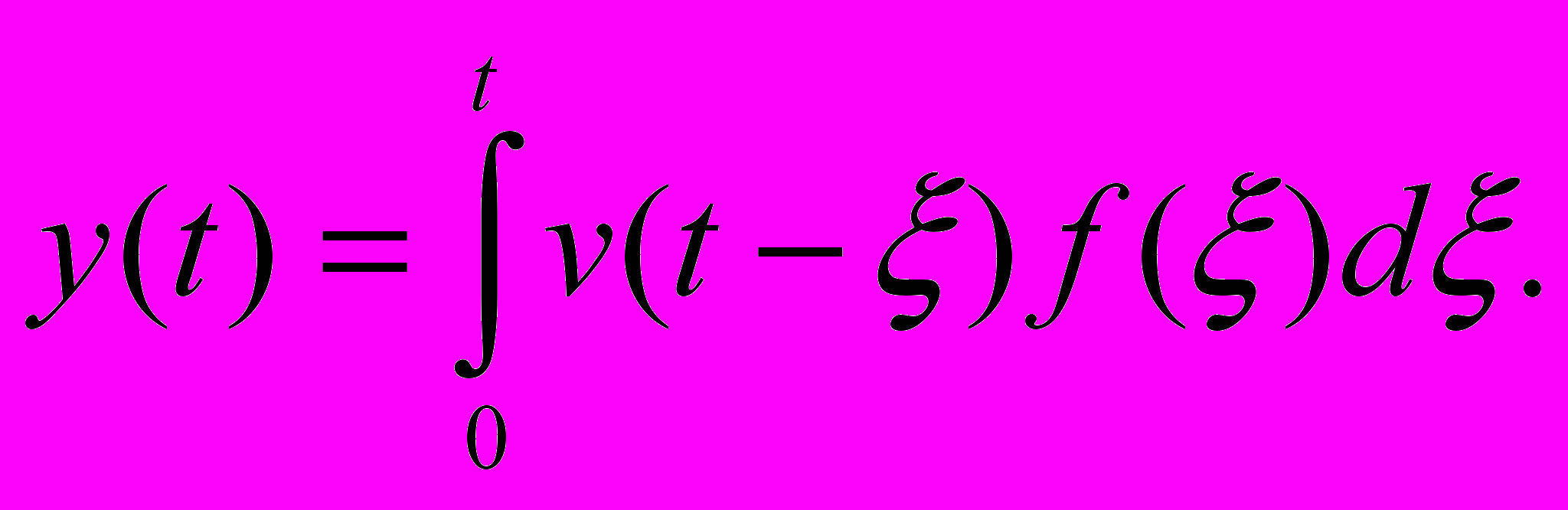Интеграл в правой части формулы (*) называется интегралом Дюамеля, а сама формула- формулой Дюамеля. В нашем частном случае

(**)

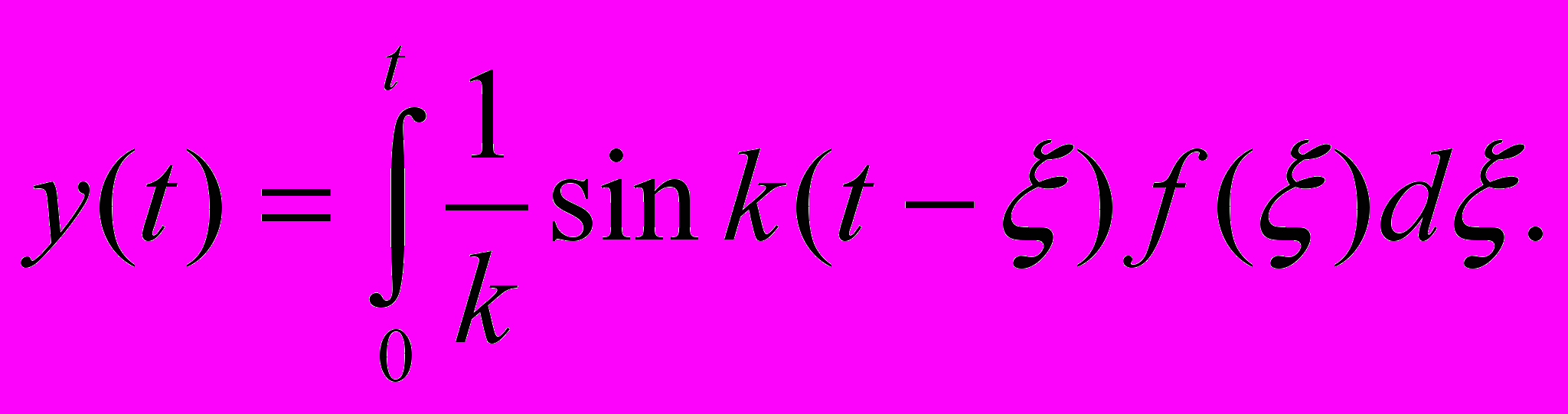Таким образом, можно, получив решение задачи Коши (II) для однородного уравнения, соответствующего данному неоднородному уравнению, вместо метода вариации произвольных постоянных применить формулу (*) и найти решение задачи Коши(I) для неоднородного уравнения с однородными (равными нулю) начальными условиями.


Разъясним, какой физический смысл можно этому придать.


^ Метод импульсов.


Рассмотрим бесконечное множество задач с неизвестными функциями


(I)

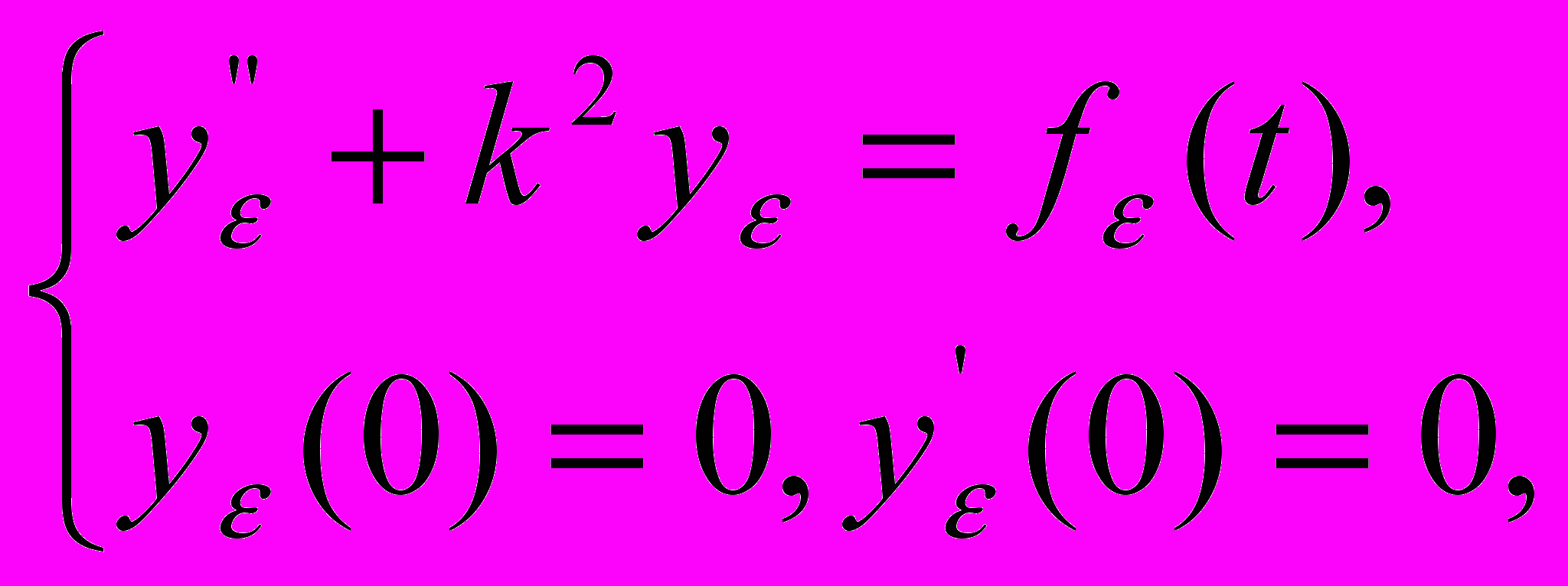
где функция f(t) отлична от нуля в интервале (0, ) и равна нулю вне этого интервала. Будем еще считать, что 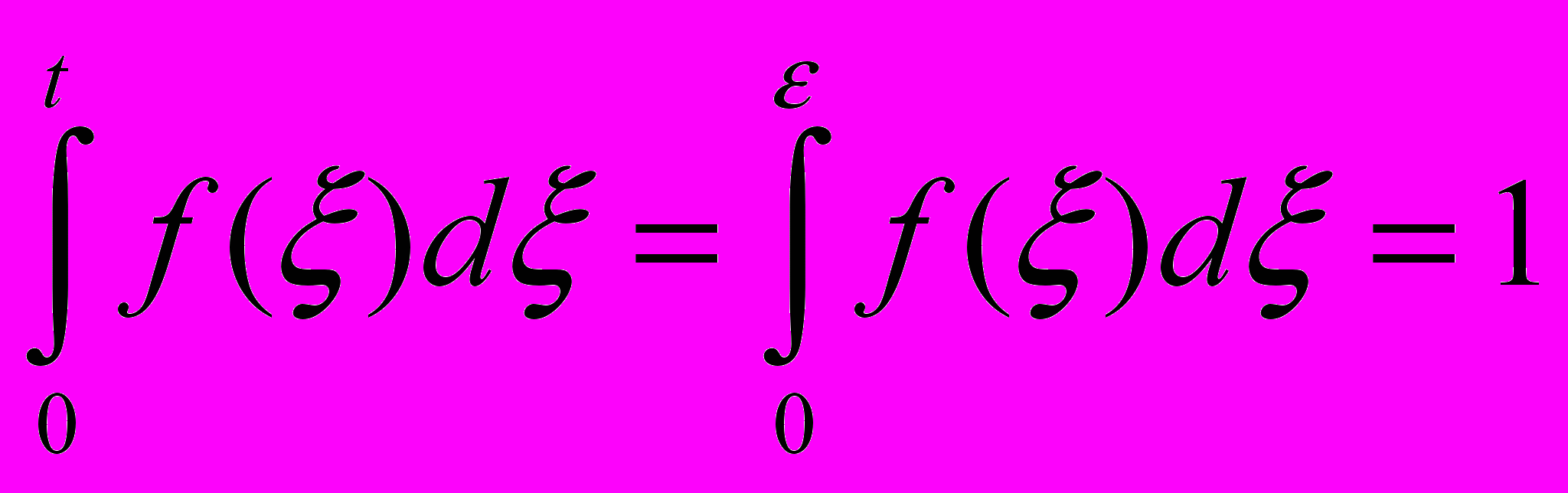(вскоре мы придадим этому условию определенный физический смысл). По формуле (**)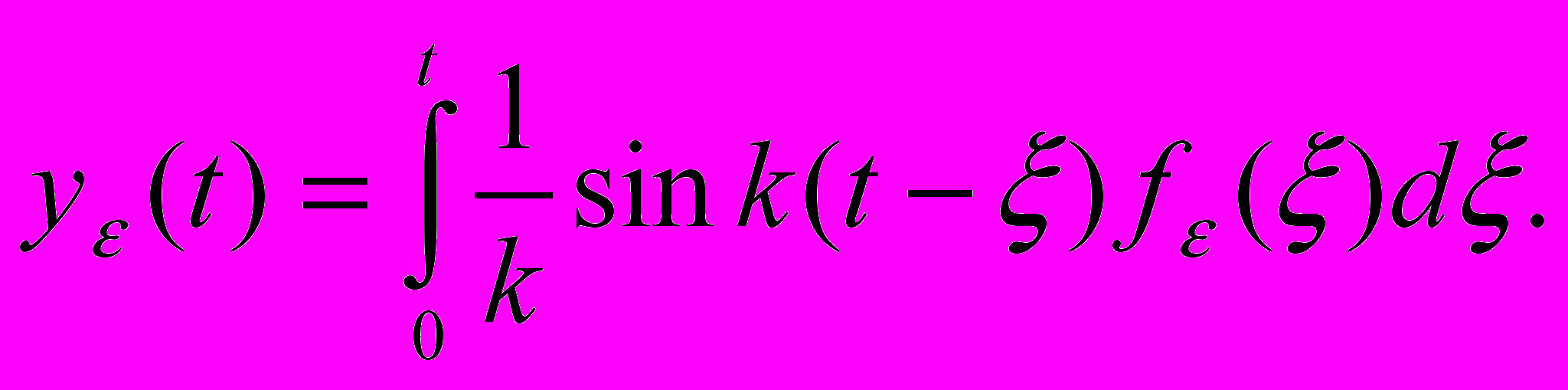



Пусть f(t)- сила, действующая на некоторую систему, а y(t)- смещение этой системы.

Пусть при t<0 система находилась в состоянии покоя (значит, y(0)=0, y’(0)=0). Пусть смещение системы происходит под действием силы f(t), которую мы ввели. Тогда

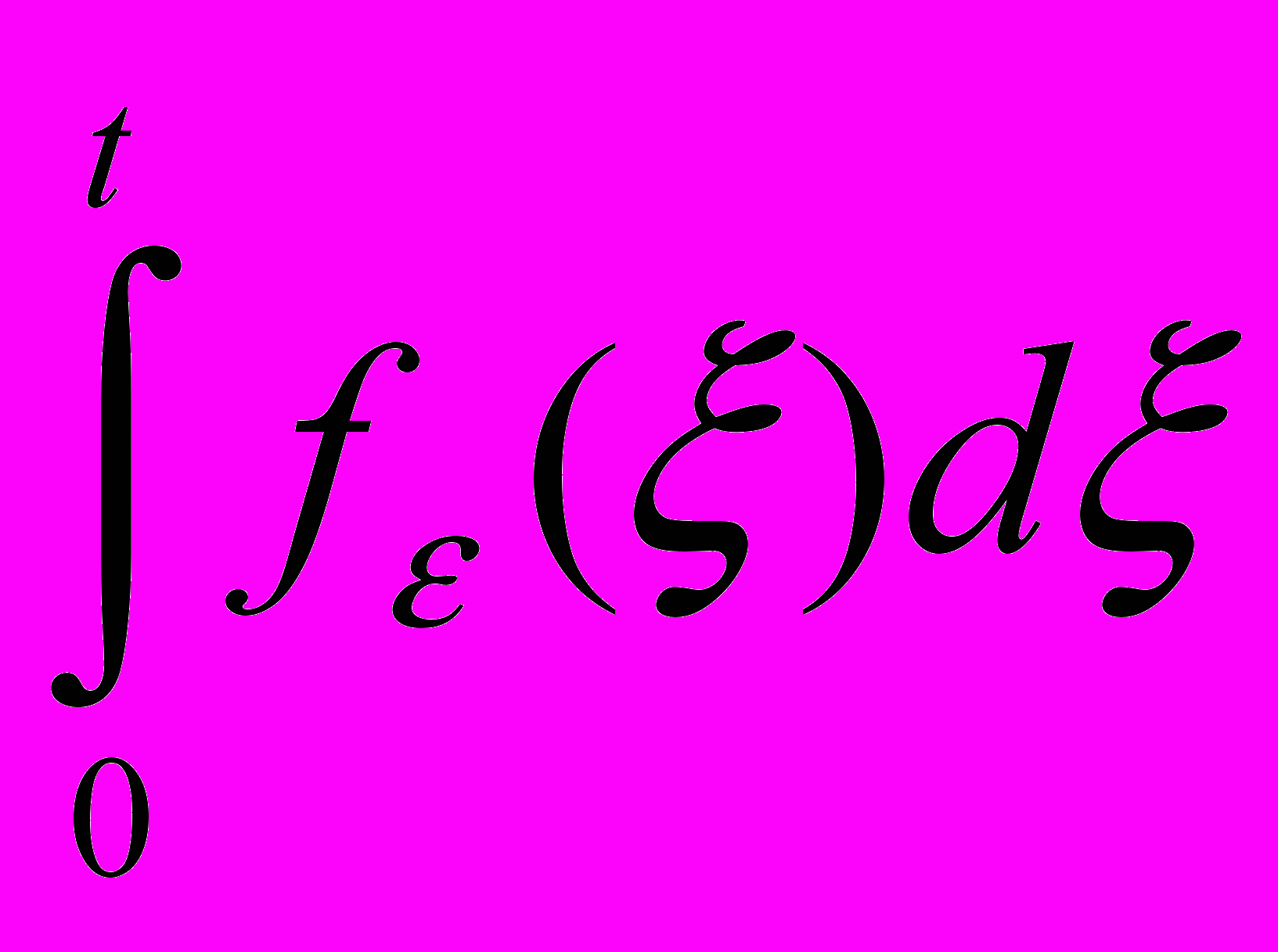есть импульс J(t) силы f(t) на промежутке времени (0, t), а решение задачи Коши (I) есть функция влияния этого импульса. По нашему предположению J(t)=1.

Рассмотрим  как параметр. Повторим формулу для y(t):




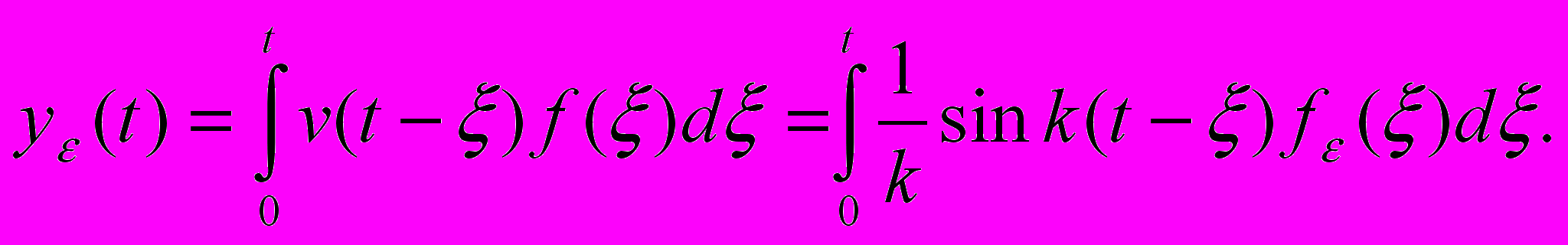
Применим к интегралу теорему о среднем и получим:




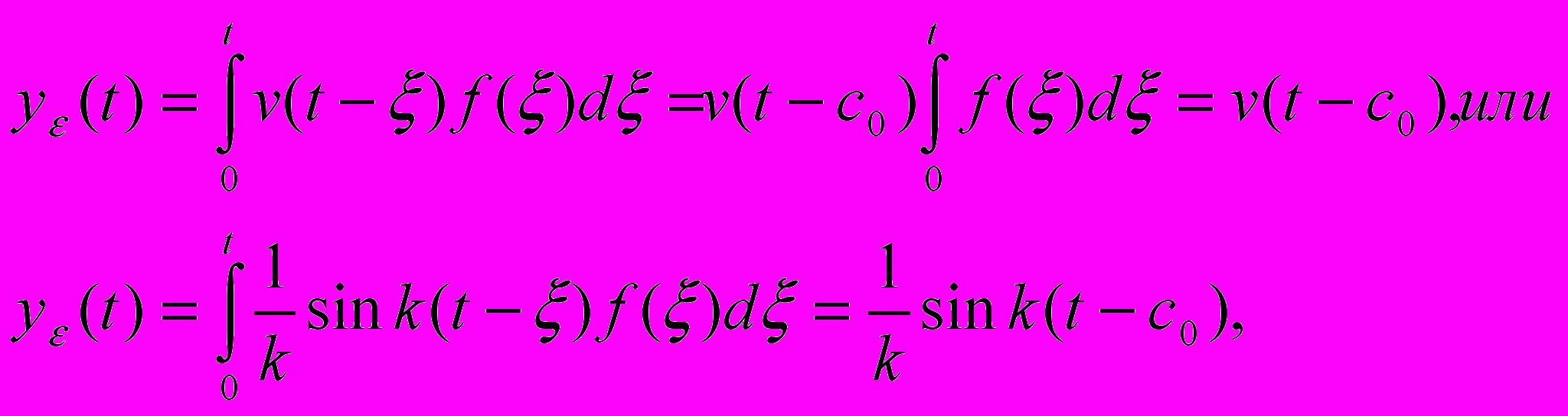
где с0- точка, 00<. Тогда



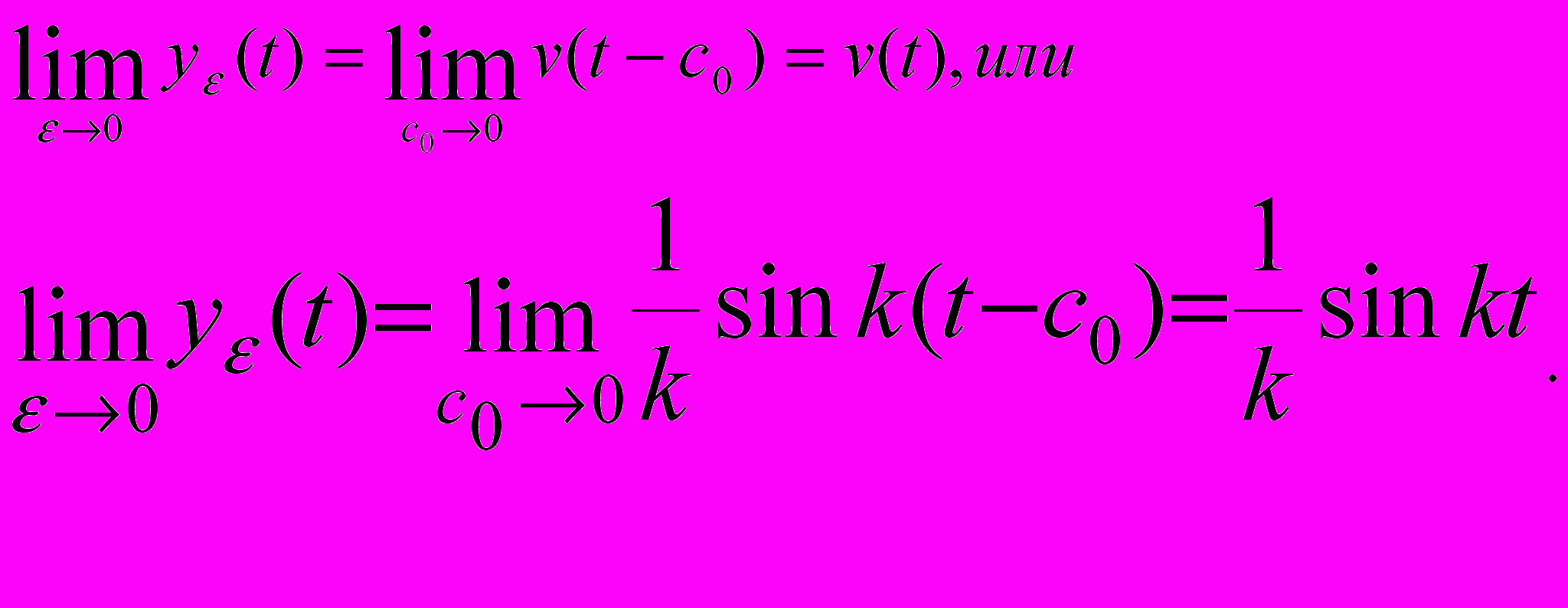
Заметим, что когда 0, сила f(t) и импульс этой силы действуют на участке времени, стремящемся к нулю (в то же время для любого  J(t)=1 по предположению). Поэтому

функцию 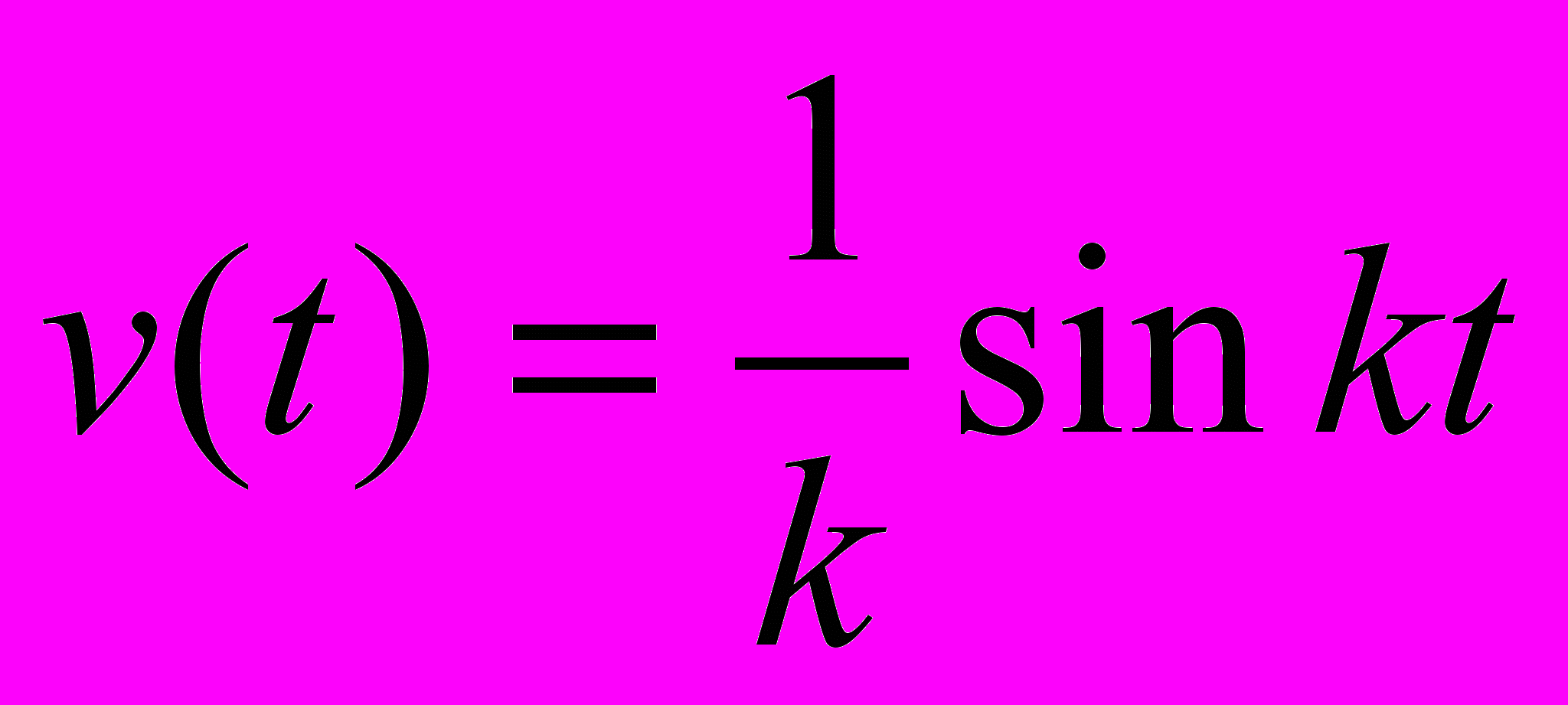можно назвать функцией влияния мгновенного импульса (действующего в момент t=0).

Замечание. Пусть y(t)- координата точки, движущейся по оси y. Если в момент t=t0

координата точки не меняется, а скорость получает конечное приращение, то такое воздействие на точку называется толчком (или мгновенным ударом). Примером служит резкий удар кием по биллиардному шару.

Итак, решение v(t) задачи Коши (II) есть функция влияния мгновенного импульса силы:



(При этом говорят, что интенсивность мгновенного импульса равна единице).


Теперь разъясним физический смысл формулы Дюамеля. Для этого разделим интервал времени (0, t) на n равных частей 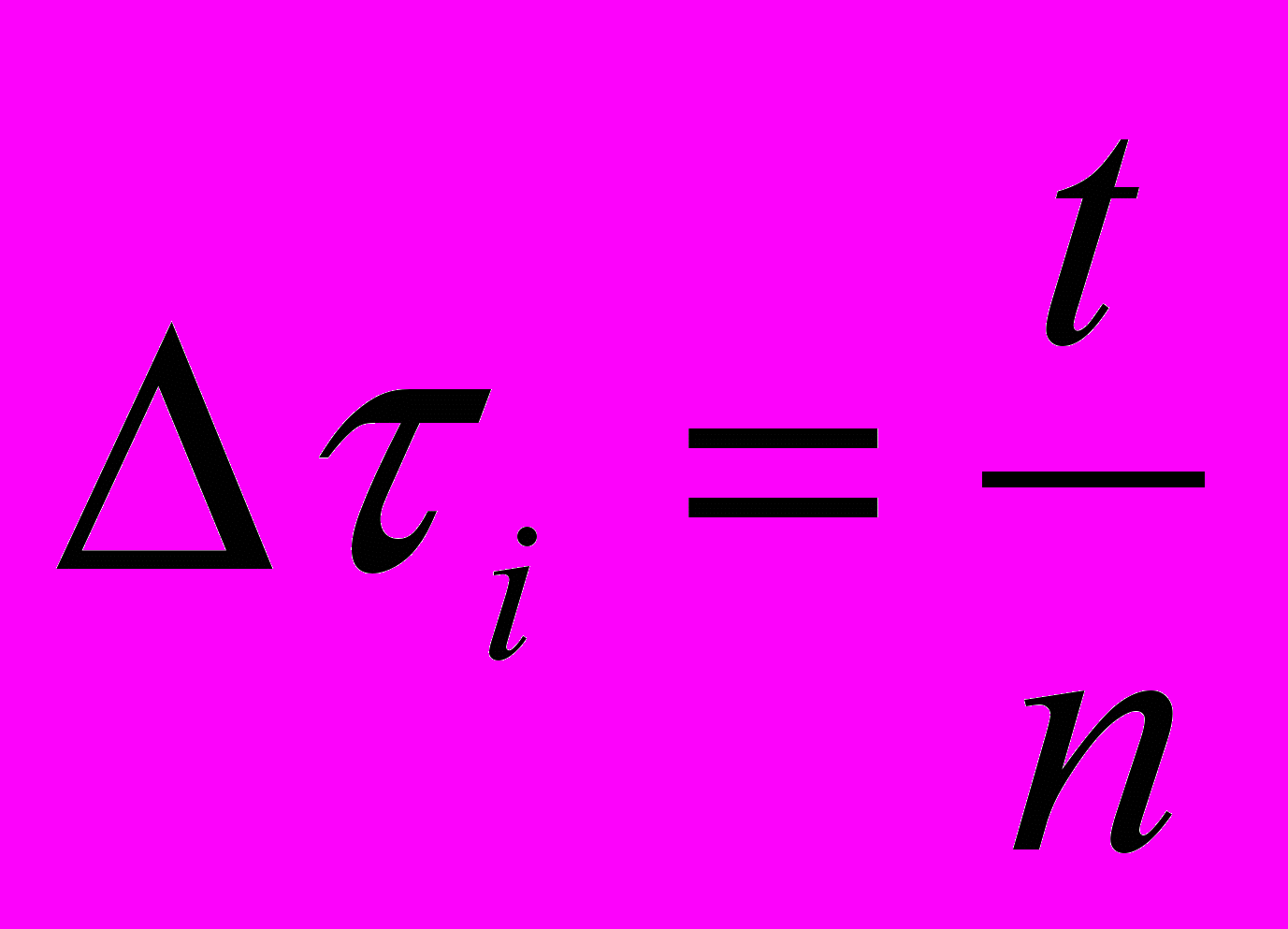точками и рассмотрим n задач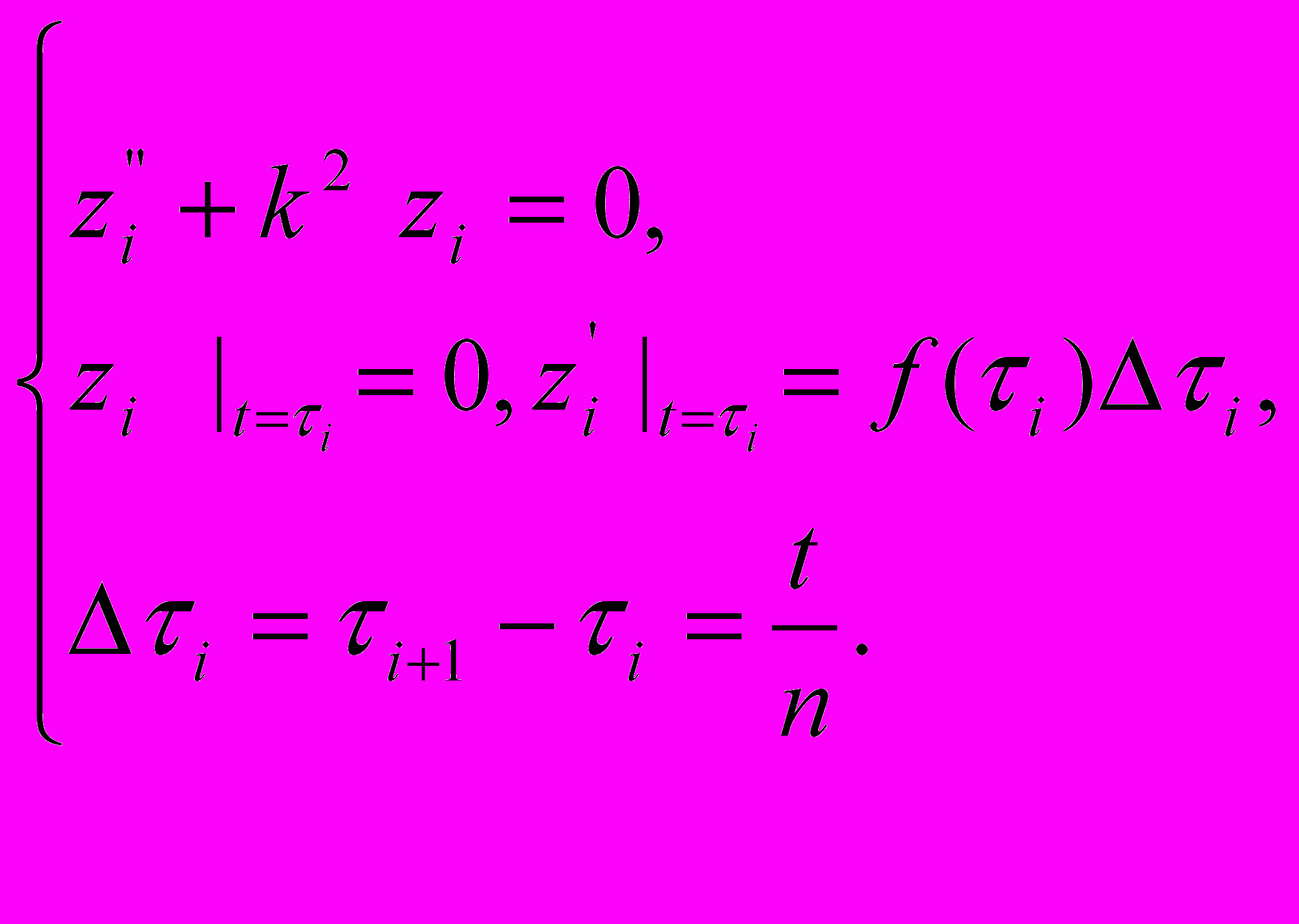

Каждая из функций zi(t) представляет собой функцию влияния мгновенного импульса интенсивности f(i)i.

Записав zi(t) как 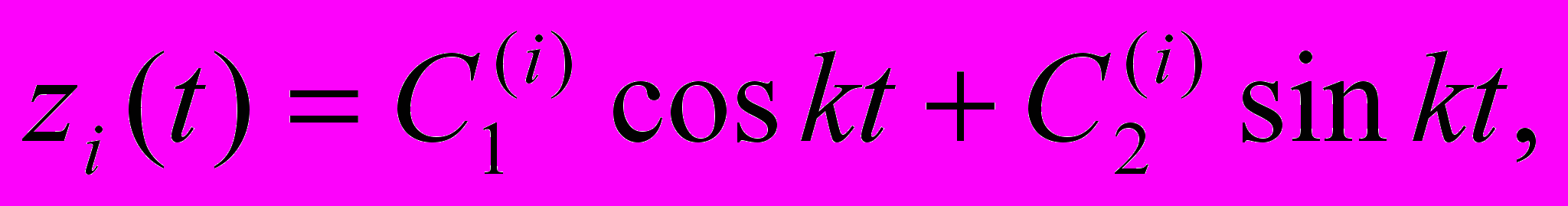используем начальные условия и найдем тем же способом, как мы это делали в случае решения задачи (I) на стр.2, что

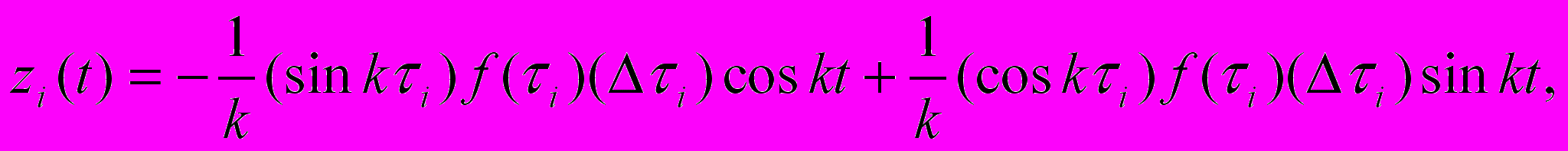а после преобразований-

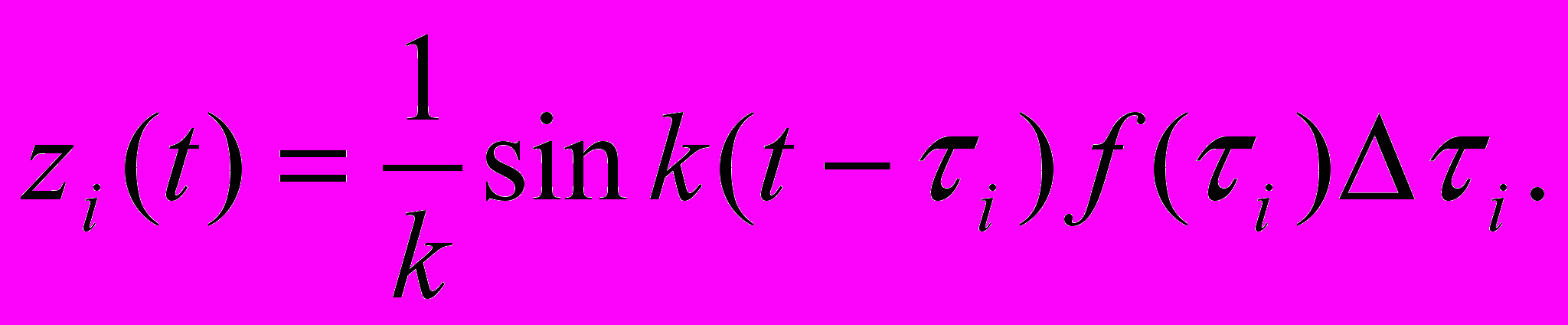Эта функция представляет собой функцию влияния мгновенного импульса интенсивности f(i)i.


Вернемся к формуле Дюамеля (**) на стр.2:



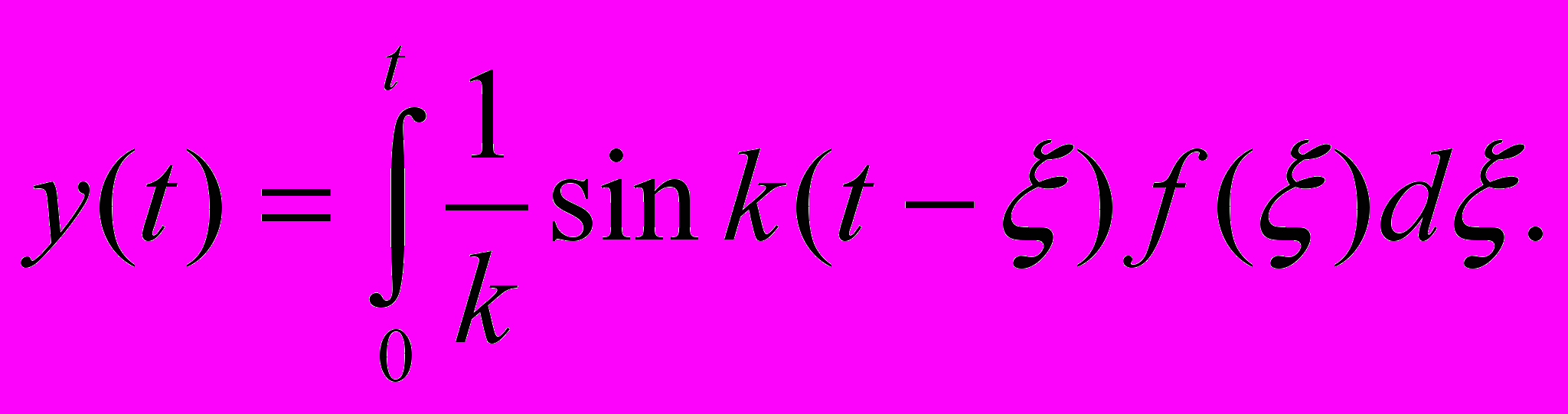
Воспользуемся определением интеграла по отрезку и запишем



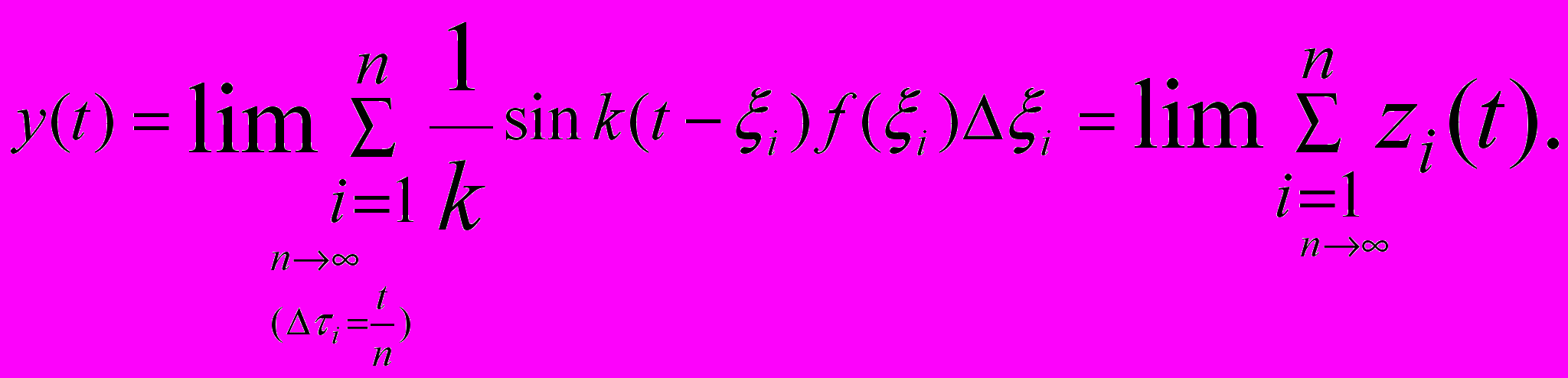
y(t)- функция влияния импульса силы 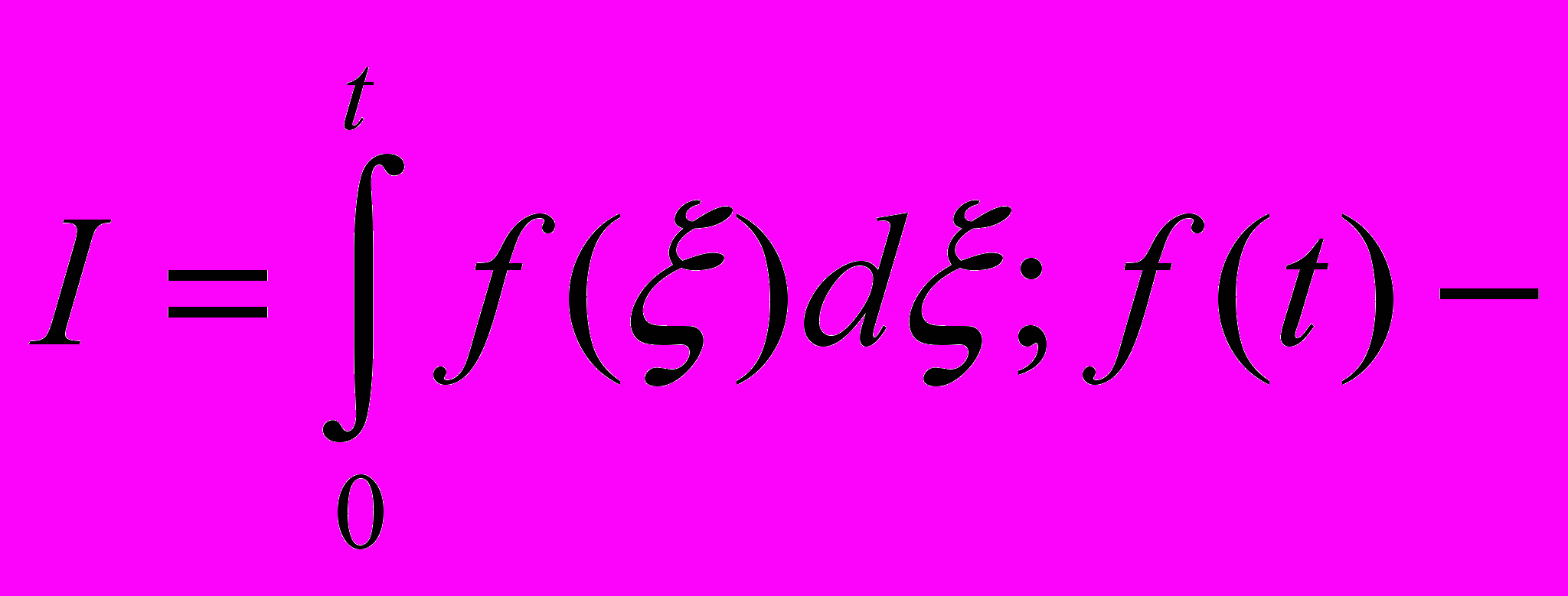непрерывно действующая на систему сила.

Если n достаточно велико, а значит, промежутки времени ii+1i малы, можно с большой точностью считать, что

()

Эта последняя формула показывает, что функция влияния импульса непрерывно действующей силы есть сумма (суперпозиция, наложение) функций влияния мгновенных импульсов; каждое из слагаемых представляет собой функцию влияния мгновенного импульса интенсивности f(i)i в момент t=i. (После перехода к пределу получаем точное значение y(t) в виде интеграла). В формуле () состоит суть метода импульсов.

Если рассматриваются первоначальные задачи Коши I и II для уравнения 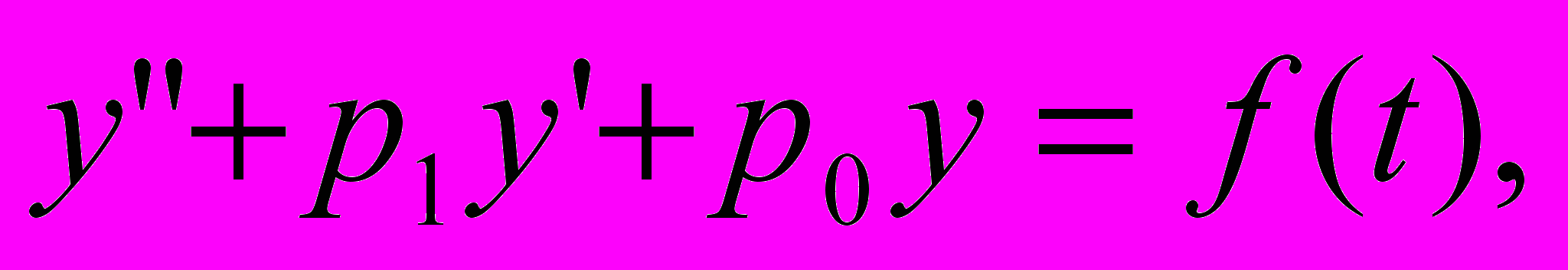то формула Дюамеля имеет вид (*):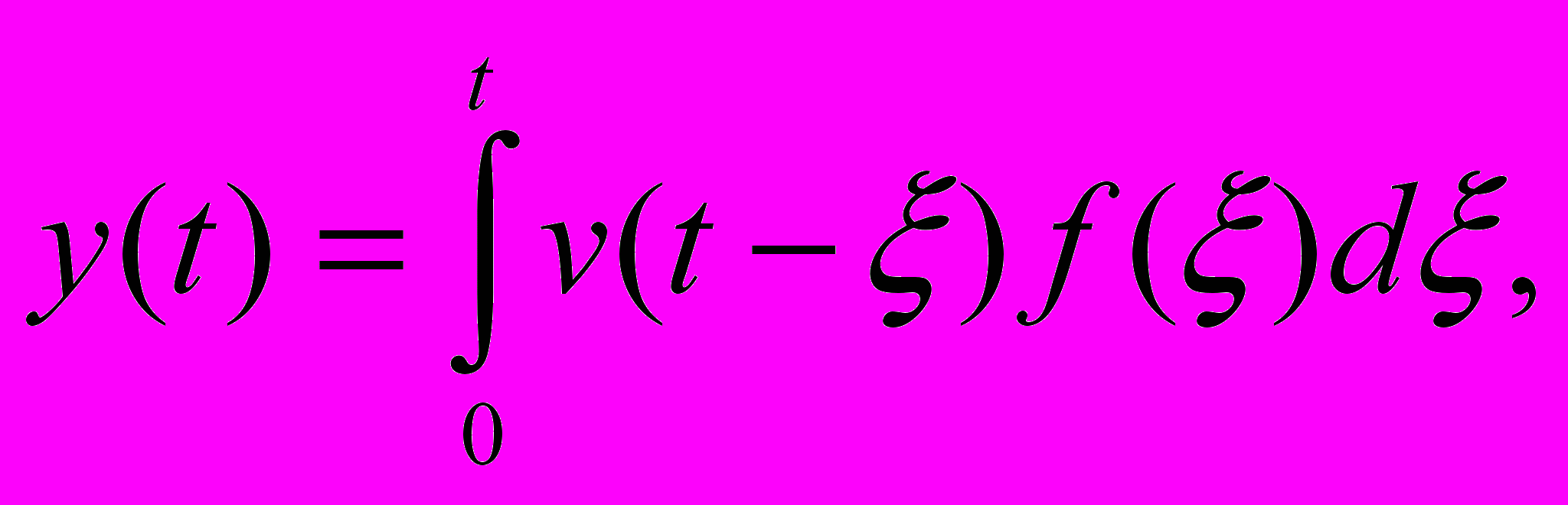

и y(t)- функция влияния непрерывно действующей силы f(t)- есть суперпозиция функций влияния мгновенных импульсов.

Итак, мы 1) решали задачу Коши I методом вариации произвольных постоянных; 2) полученную для y(t) формулу переписали в виде интеграла Дюамеля; 3) придавая функциям f(t), y(t), v(t) физический смысл, показали, что метод вариации можно рассматривать как метод импульсов. Формула Дюамеля при этом связывает между собой решение задачи Коши I для неоднородного уравнения с однородными начальными условиями с задачей Коши II для однородного уравнения, соответствующего данному неоднородному, в которой сама функция v(t) в начальный момент времени равна 0, а производная v’(0)= некоторая постоянная, значения которой связаны с функцией f(t).

v’(0)- скорость, которая сообщается системе при t=0. На практике (если, скажем, система есть натянутая струна) такую скорость можно сообщить системе в момент t=0, ударив по ней тонким молоточком.


^ Принцип Дюамеля для дифференциальных уравнений с частными производными.


Рассмотрим дифференциальное уравнение



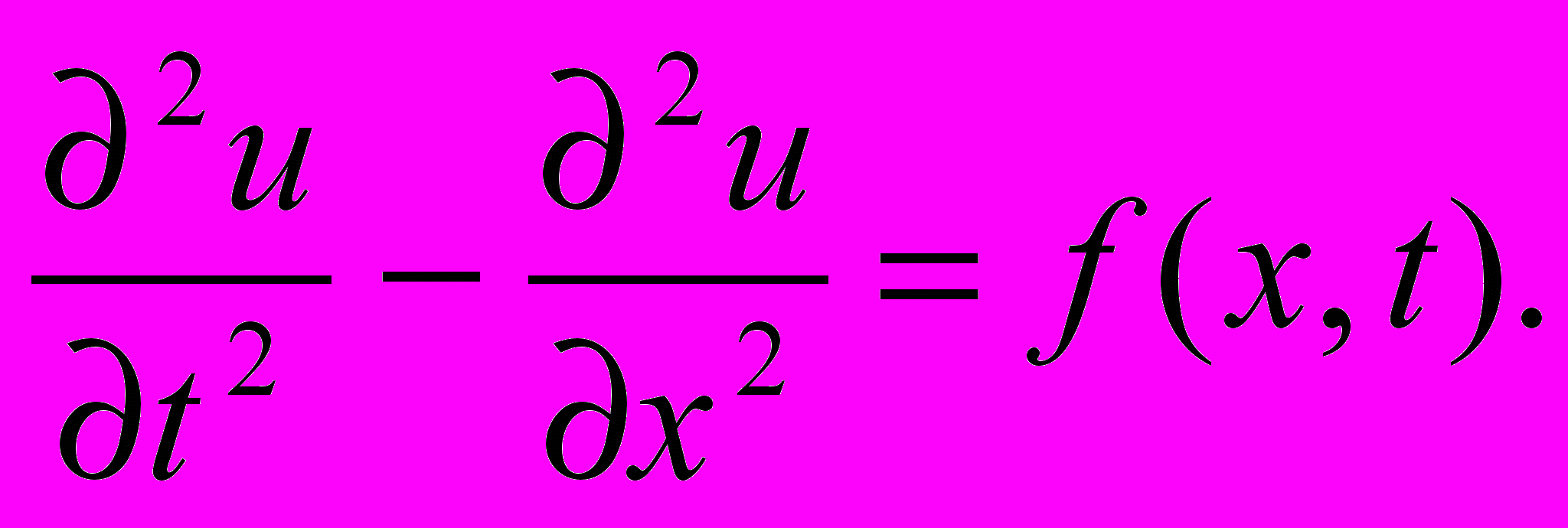
Поставим задачу Коши



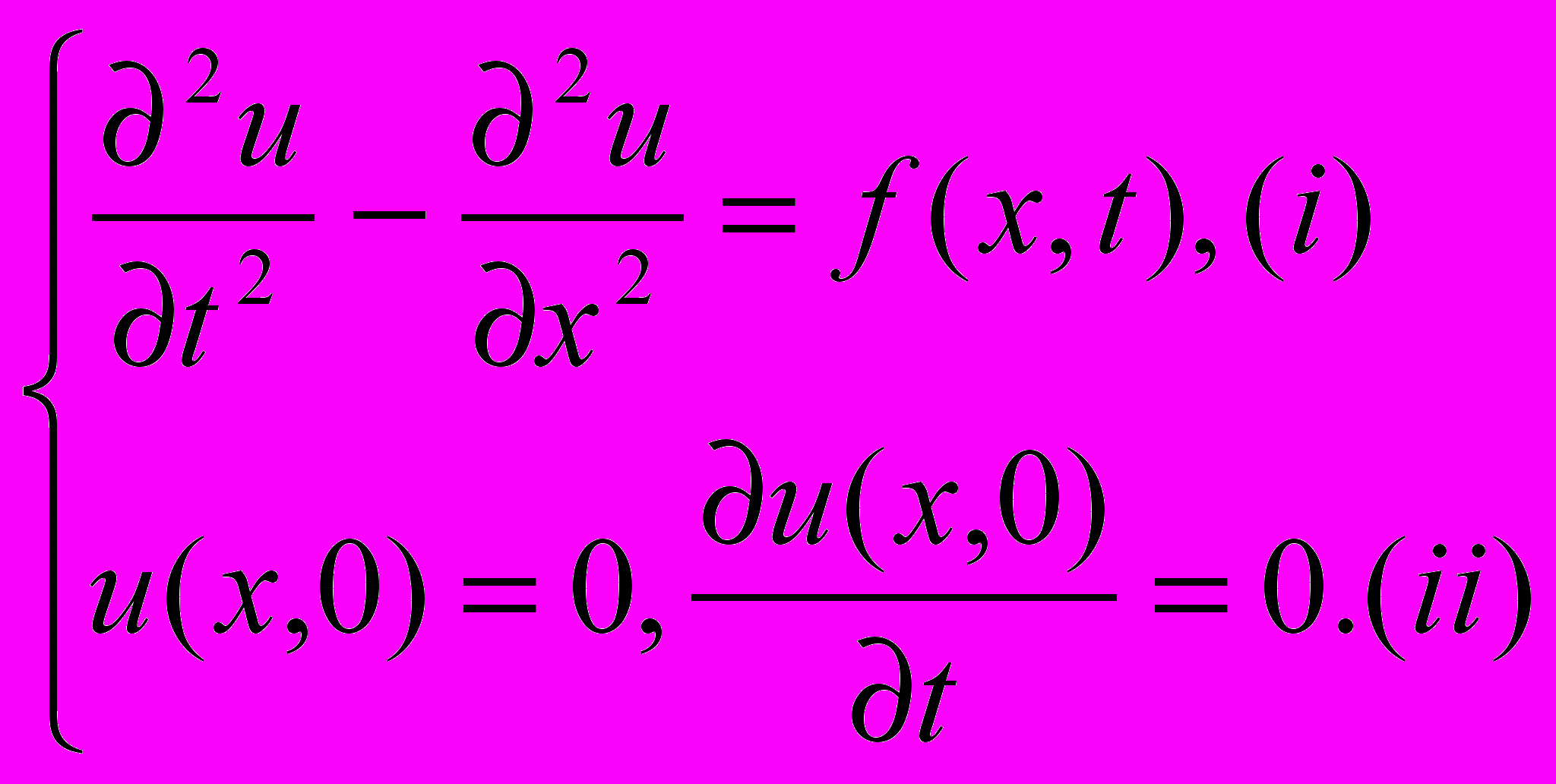
Как и в случае обыкновенного дифференциального уравнения, рассматриваем функцию f(x, t) как внешнюю силу, действующую на некоторую систему. Поскольку мы знаем, что уравнение (i), в частности, описывает колебания струны, то под f(x, t) можно понимать некоторую внешнюю силу, которая непрерывно действует на струну.

Кроме задачи (i)-(ii) рассмотрим ряд задач Коши (при различных t=) для однородных уравнений



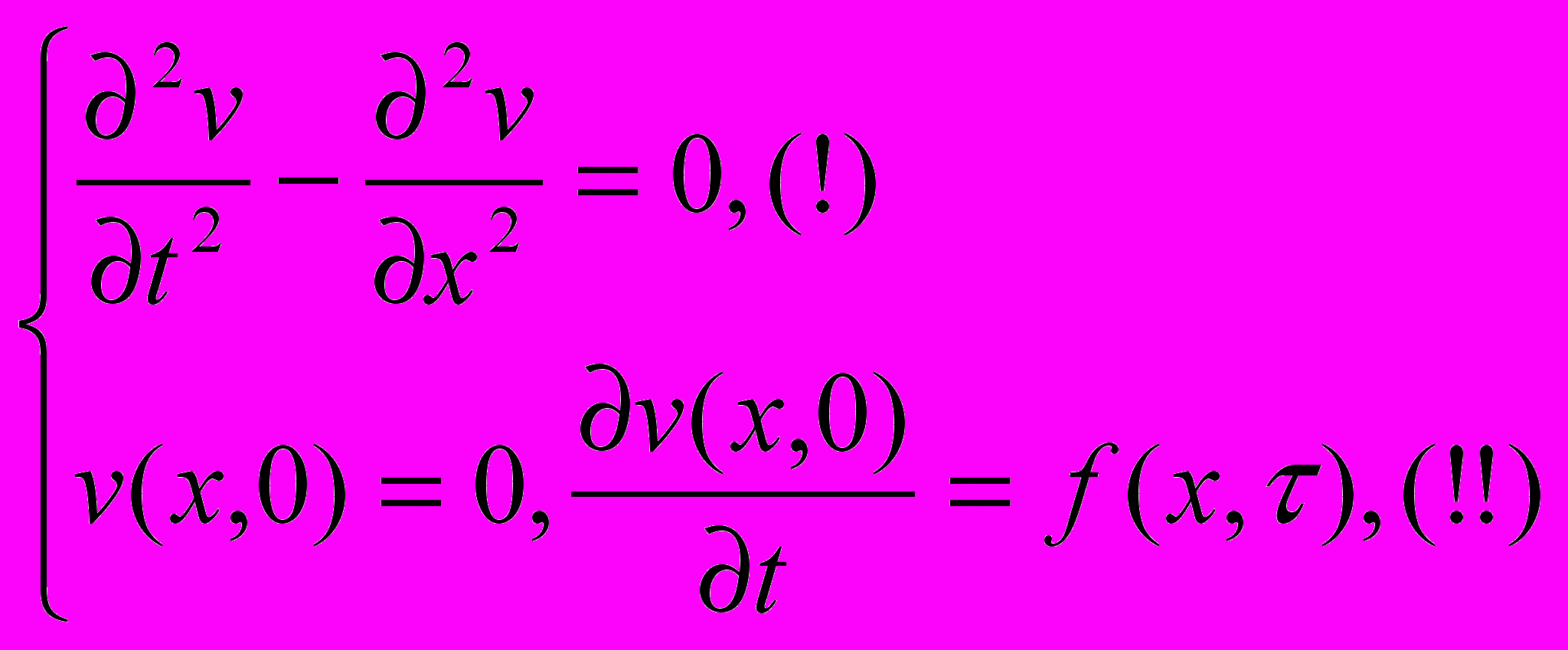
где f(x, )- значение функции f(x, t) из (!)при t=. Чтобы подчеркнуть, что функция v зависит от , будем писать v=v(x, t, ).

Решение задачи (!)-(!!) можно получить по формуле Даламбера (так, как это делалось в одной из предыдущих лекций). При этом, поскольку при t= v=0, выражение для v(x, t, )

содержит только одно слагаемое:

()

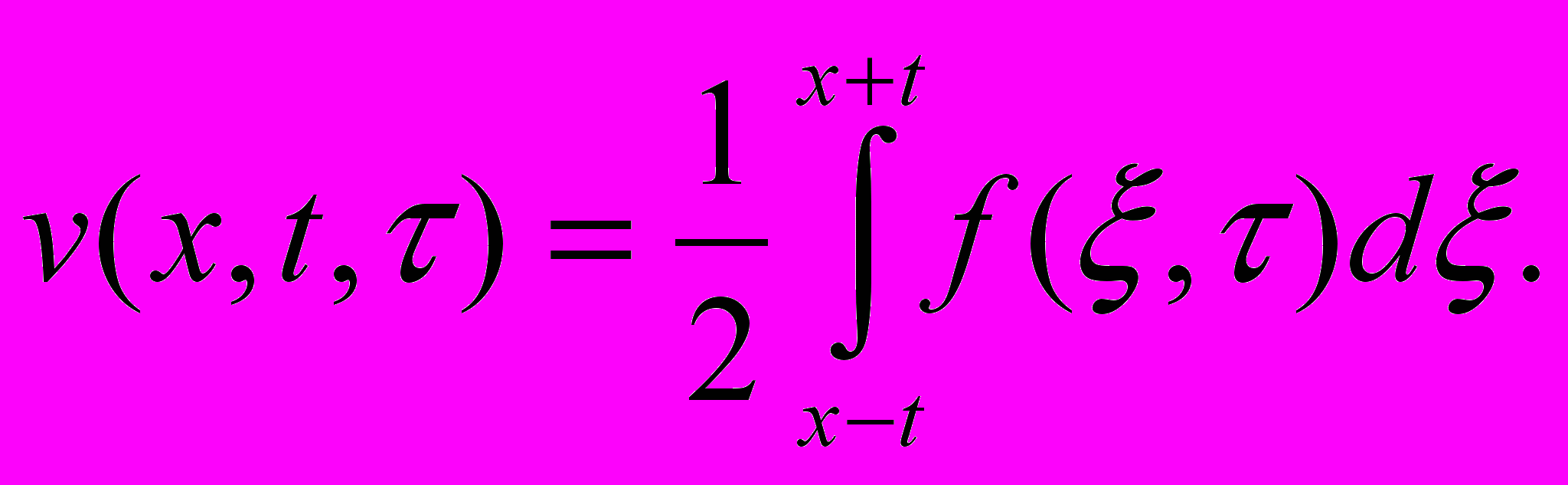Решение v(x, t, ) продолжим нулем при t. v(x, t, )- функция влияния мгновенного импульса силы интенсивности f(x, ).

Оказывается, что решение u(x, t) задачи Коши (i)-(ii) ищется по формуле Дюамеля:

()

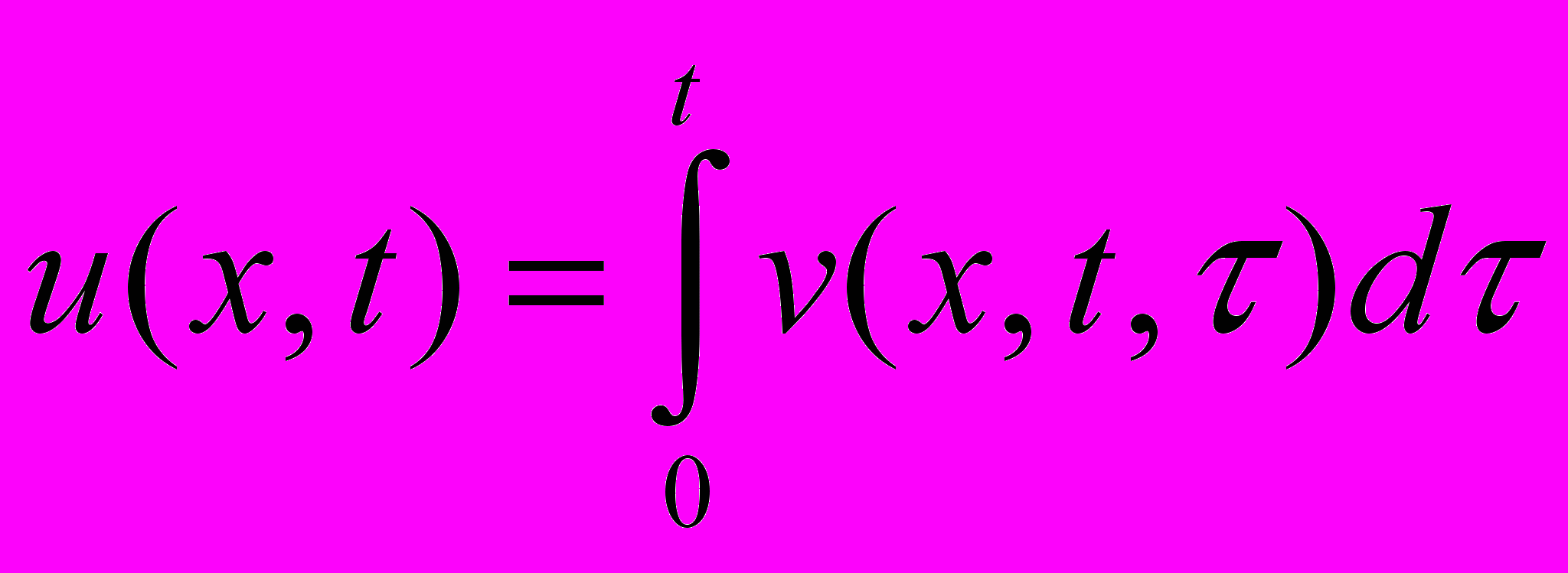(подынтегральная функция в нашем случае находится по формуле ()).

Интеграл в этой формуле называется интегралом Дюамеля. Если формула () верна, то, как и в случае с обыкновенным дифференциальным уравнением, она показывает, что

u(x, t)- функция влияния непрерывно действующей силы- есть суперпозиция функций влияния мгновенных импульсов.

Проверим, что u(x, t) из () является решением уравнения (i) и удовлетворяет

начальным условиям (ii). Итак,



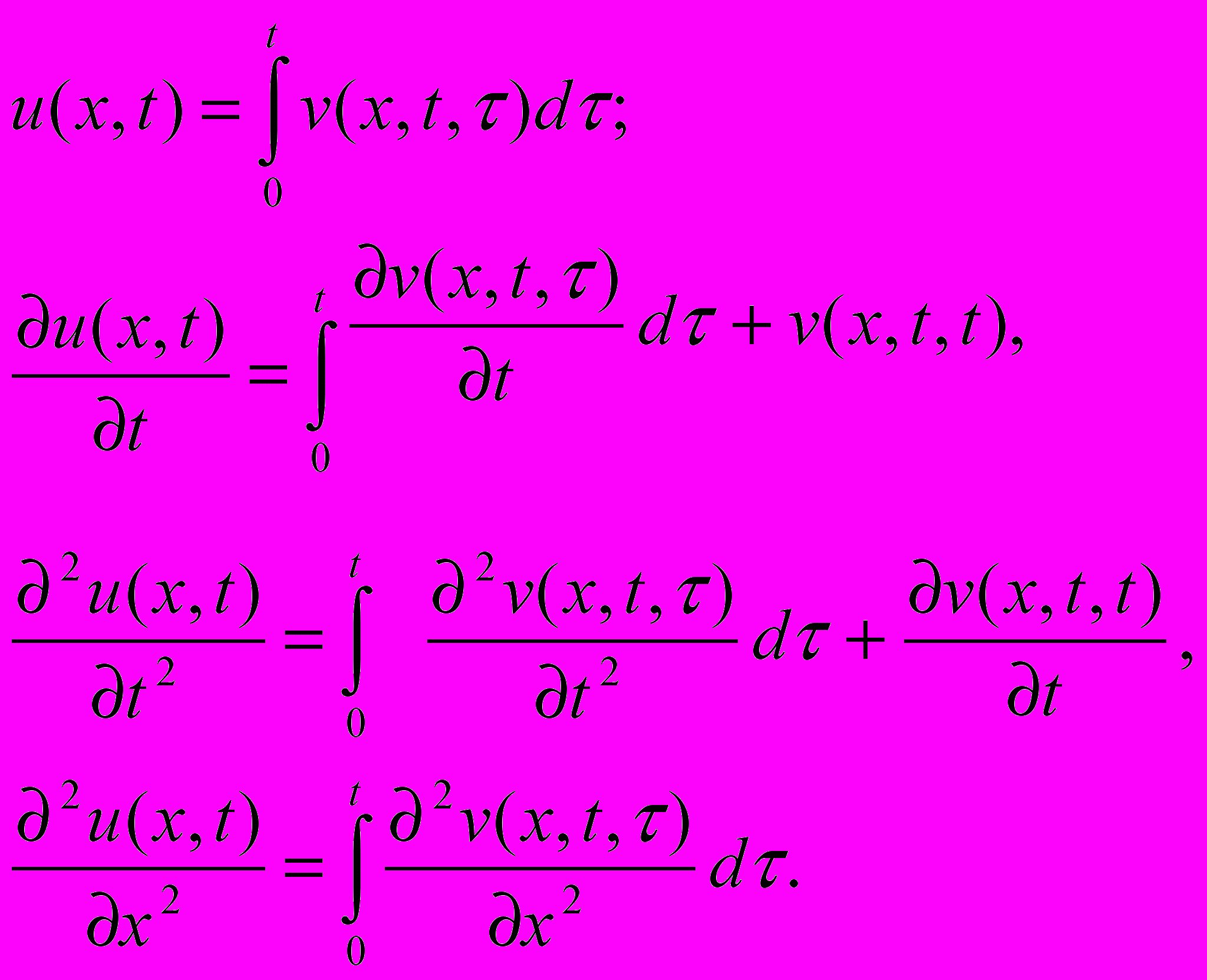
Заметим, что v(x, t, t)=0 и 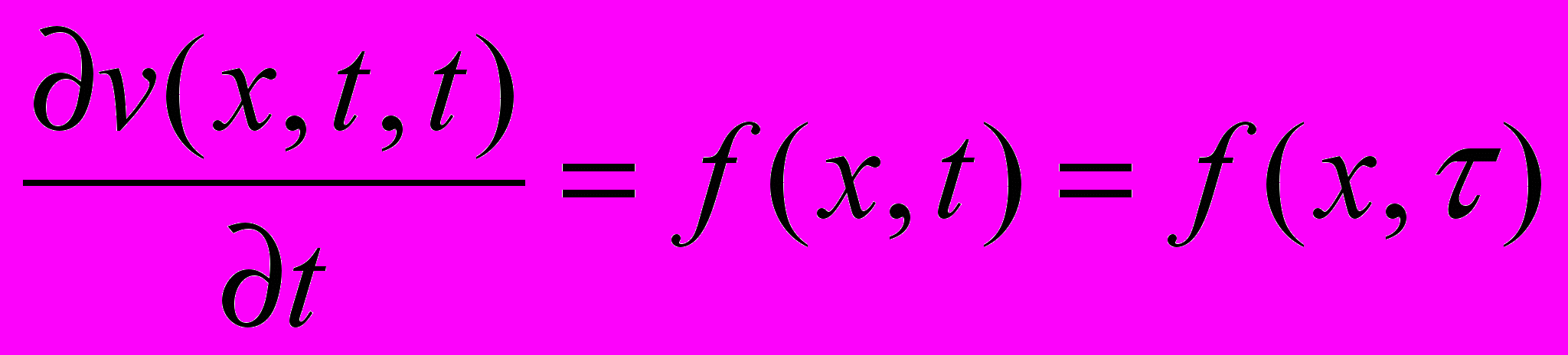по условиям (!!).

Поэтому



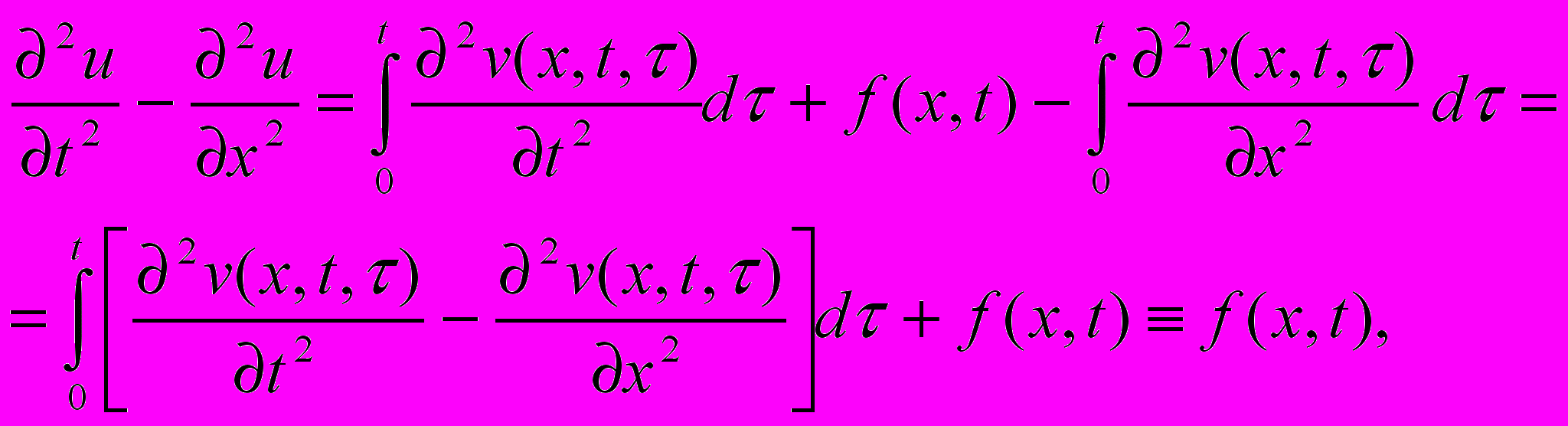
т.е. u(x, t)- решение уравнения (i). Кроме того



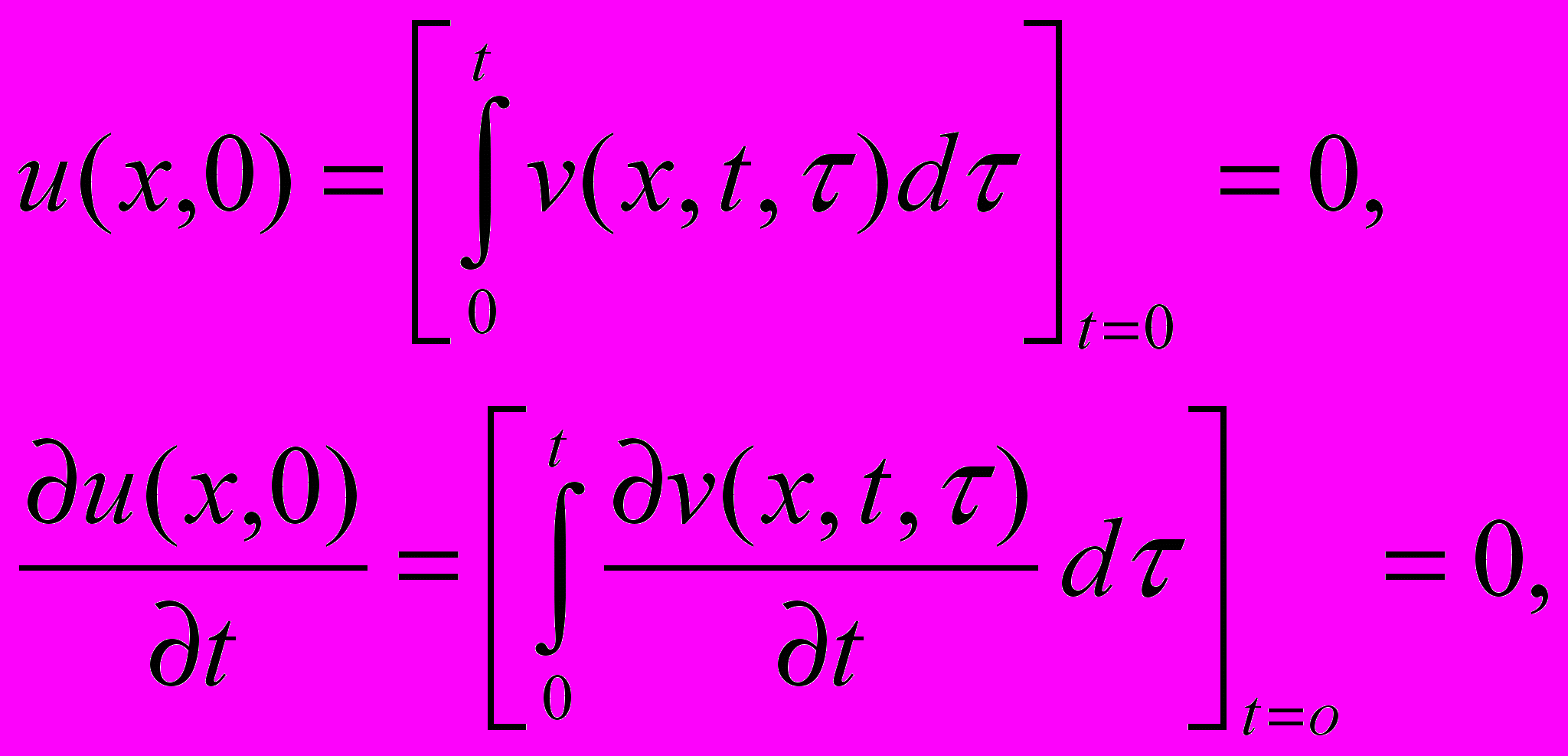
т.е. функция u(x, t) начальным условиям (ii) удовлетворяет.

Формула () дает математическое выражение принципа Дюамеля.


Физическая интерпретация этого принципа: при сложении внешних воздействий их результаты складываются, и результат воздействия на частицу (систему) непрерывно действующей силы эквивалентен воздействию континуальной (т.е. непрерывной) суммы последовательных толчков.


В теории линейных дифференциальных уравнений хорошо известен принцип суперпозиции:

Если функции ui (i=1,…,k) являются частными решениями линейных дифференциальных уравнений Lu=qi (обыкновенных или с частными производными), то сумма 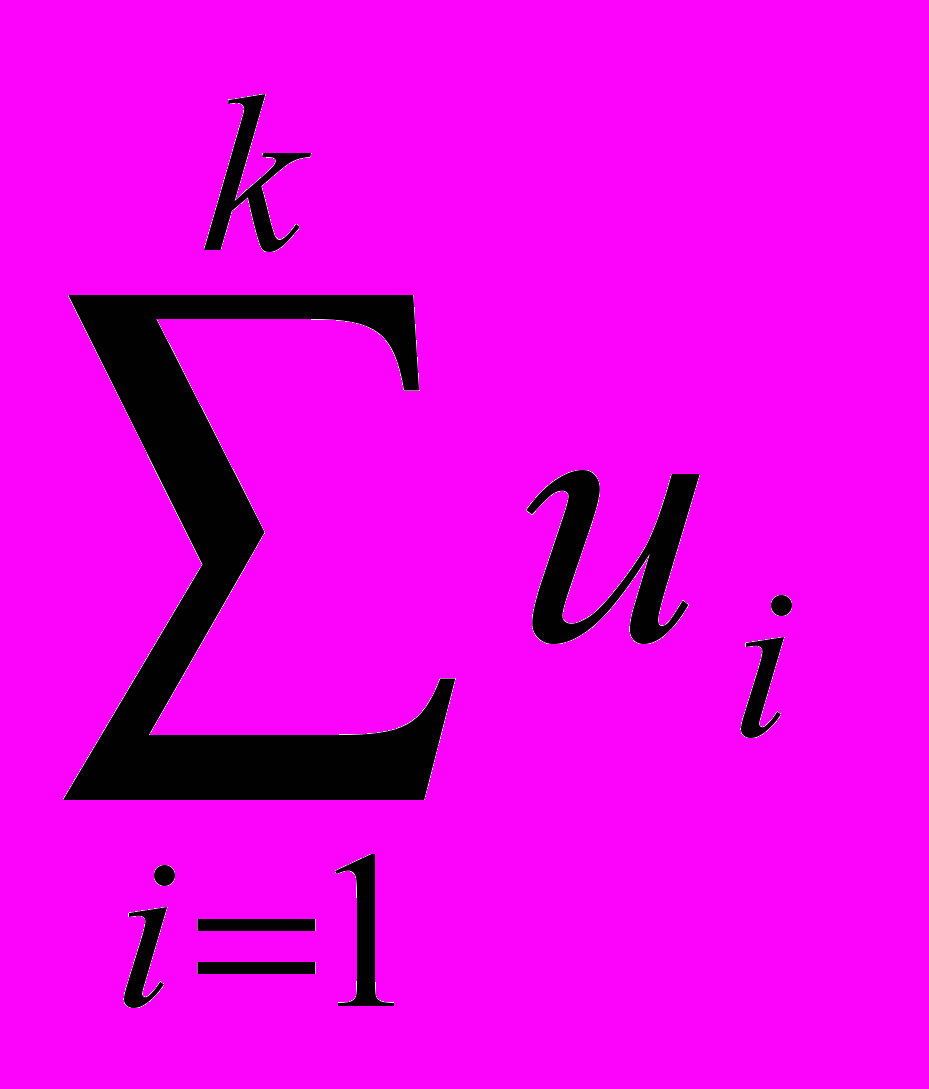является

решением уравнения

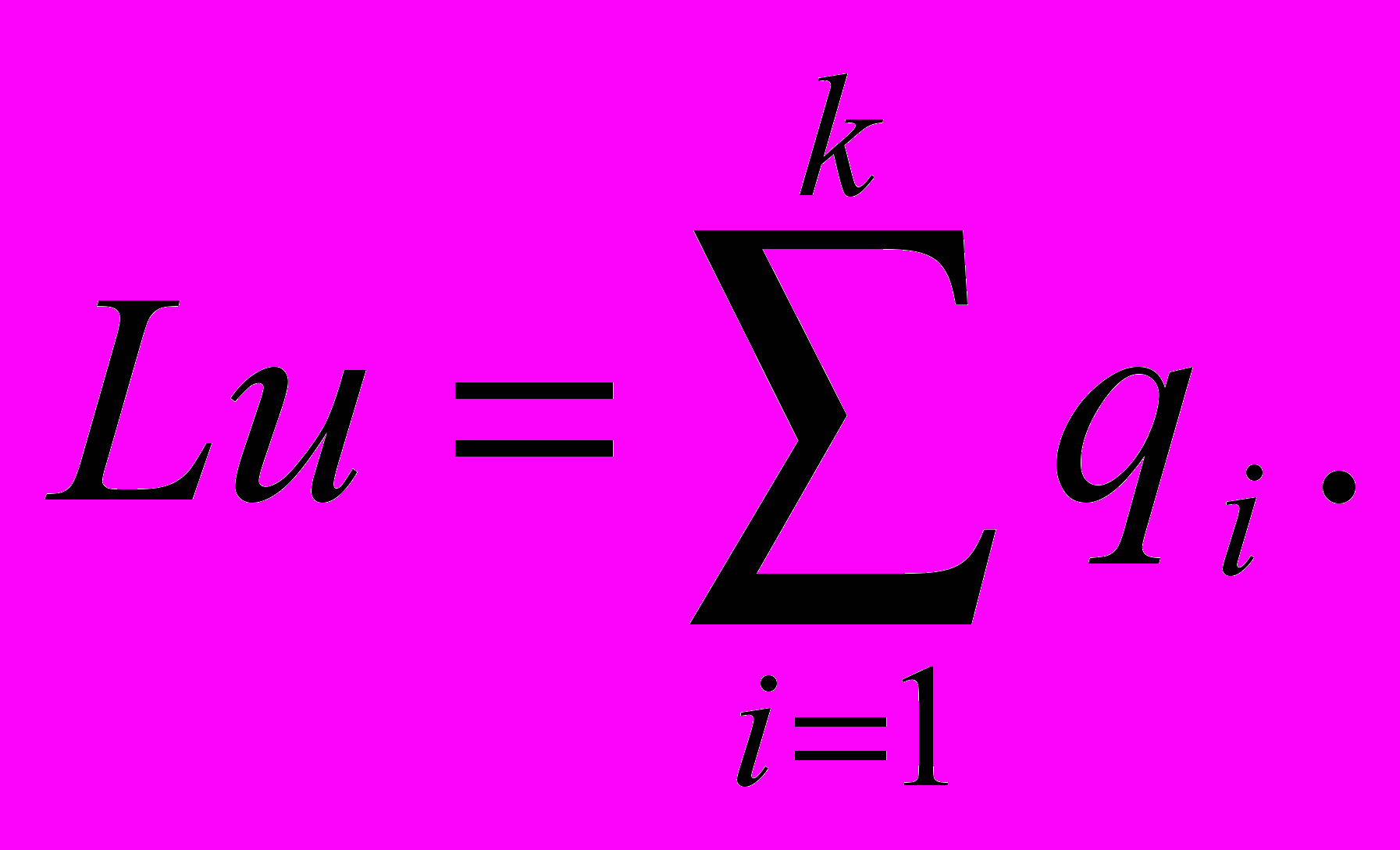
В случае, когда i меняется от 1 до бесконечности, справедлив обобщенный принцип суперпозиции, если вычисление производных от ряда 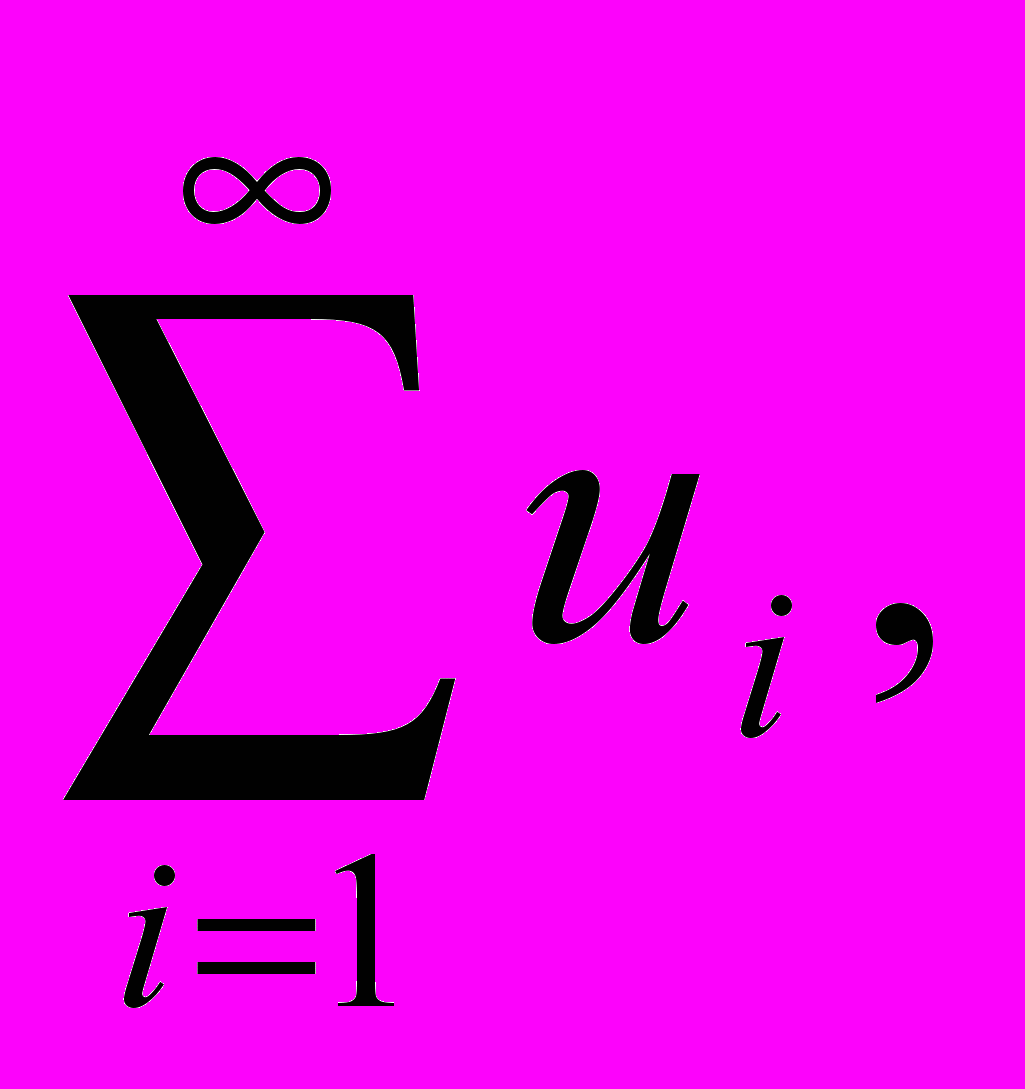фигурирующих в операторе Lu, можно совершить при помощи почленного дифференцирования этого ряда.

^ Принцип Дюамеля можно рассматривать как следствие принципа суперпозиции, и поэтому он применим только к задаче Коши для линейного дифференциального уравнения (обыкновенного или с частными производными).

Отметим некоторые случаи, в которых возможно применение принципа Дюамеля.


1.Уравнение 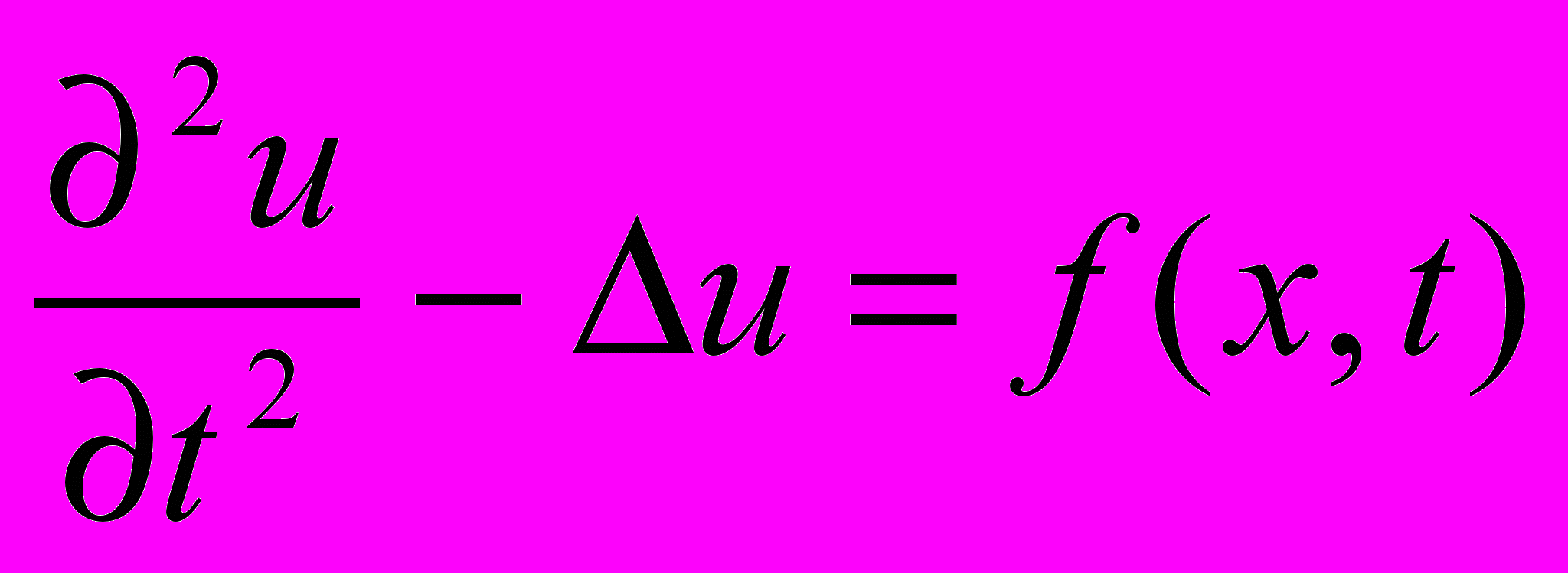с однородными начальными условиями, если x=(x1,…,xn) и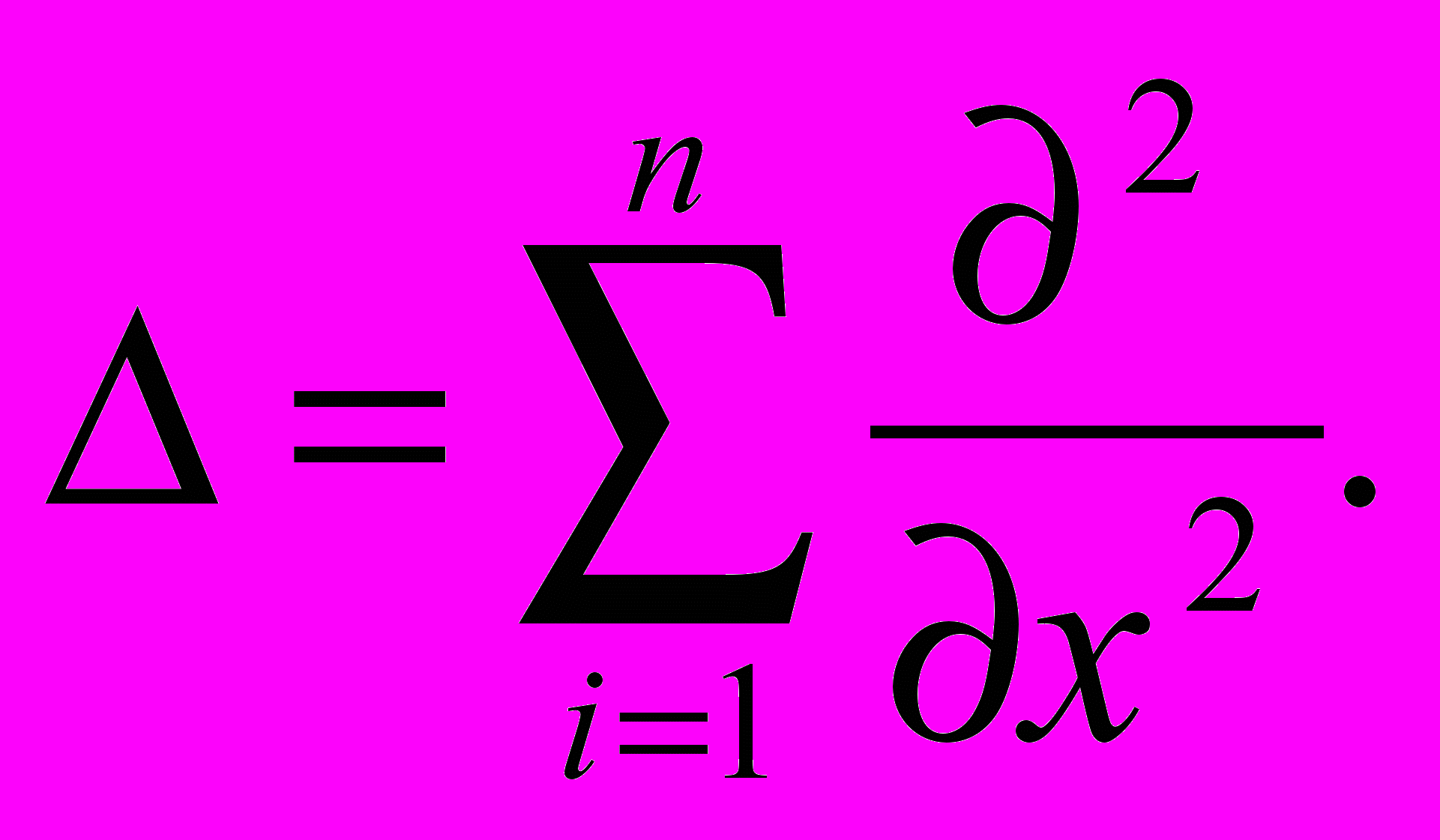

2. Уравнение 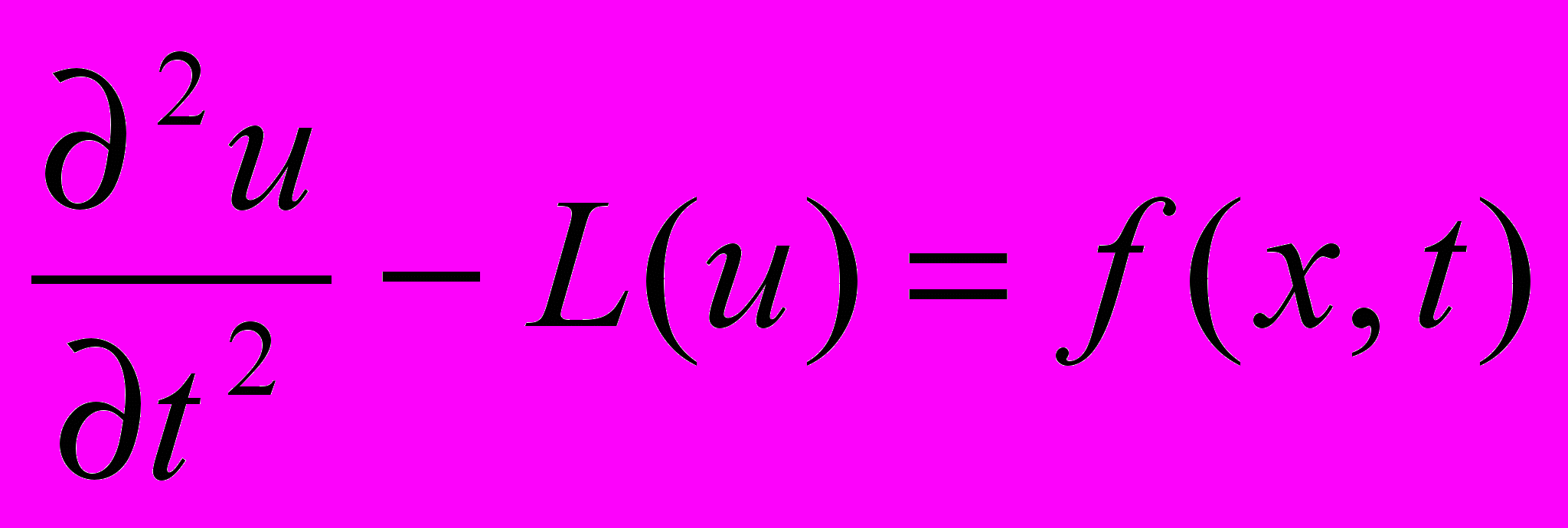с однородными начальными условиями, если x=(x1,…,xn) и L- произвольный линейный дифференциальный оператор по x и t с переменными коэффициентами, который может содержать производную по t первого порядка, но не содержит производной по t более высокого порядка.

3. Задача Коши для уравнения теплопроводности в случае, когда xR1:



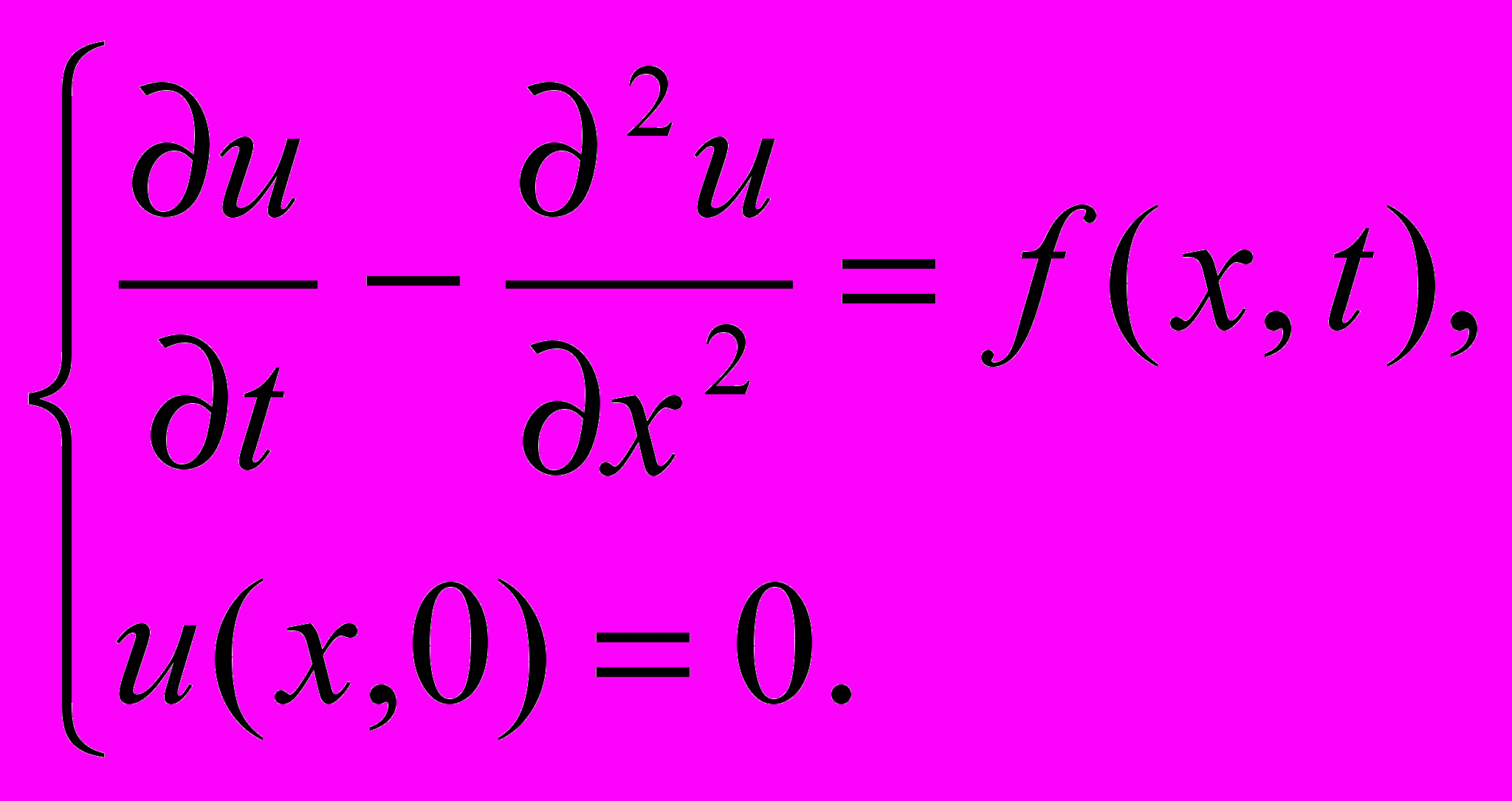
4. Задача Коши

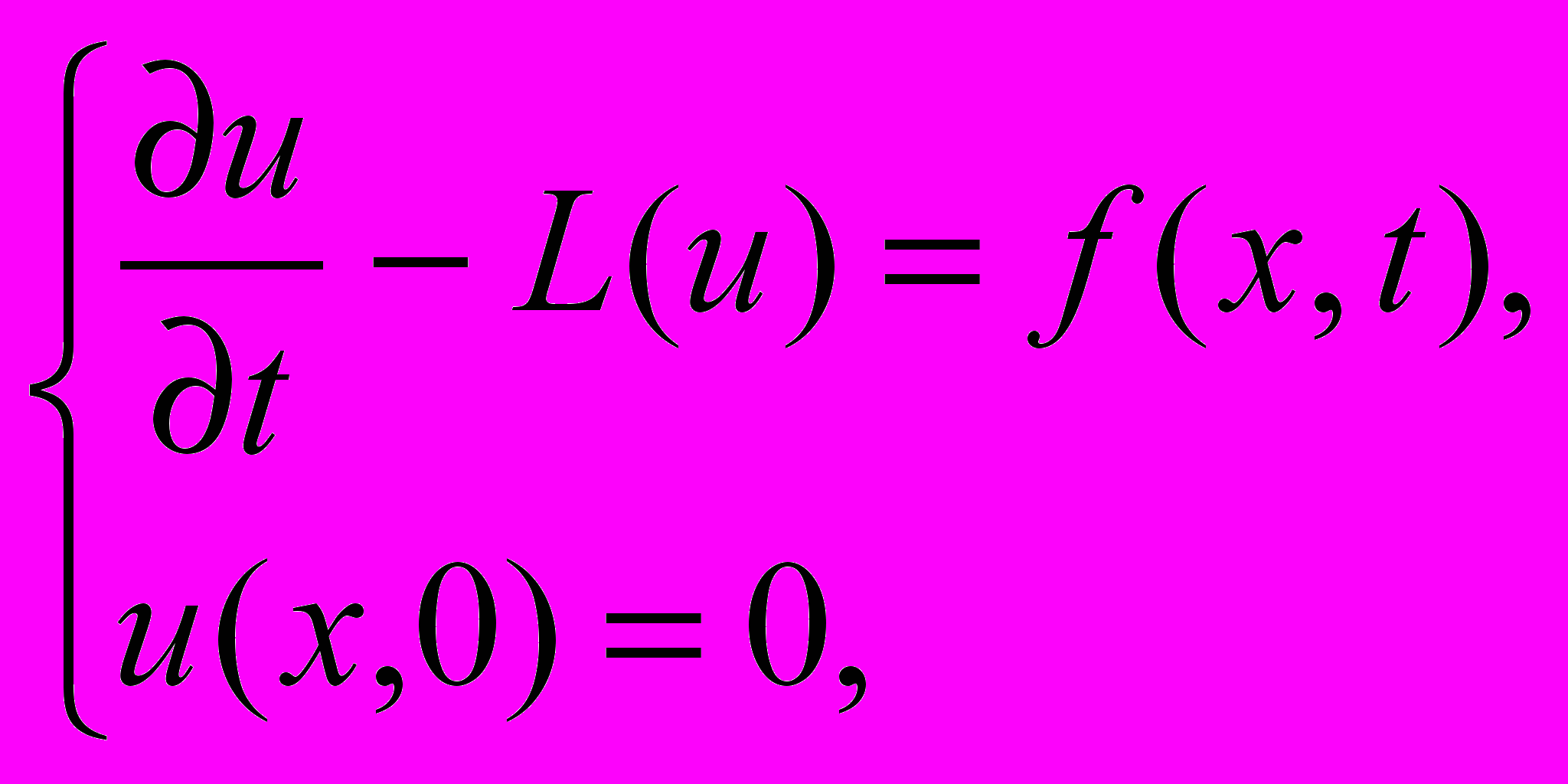если xRn, L(u)- произвольный линейный дифференциальный оператор по x c переменными коэффициентами.

5. Задача Коши для систем дифференциальных уравнений первого порядка:




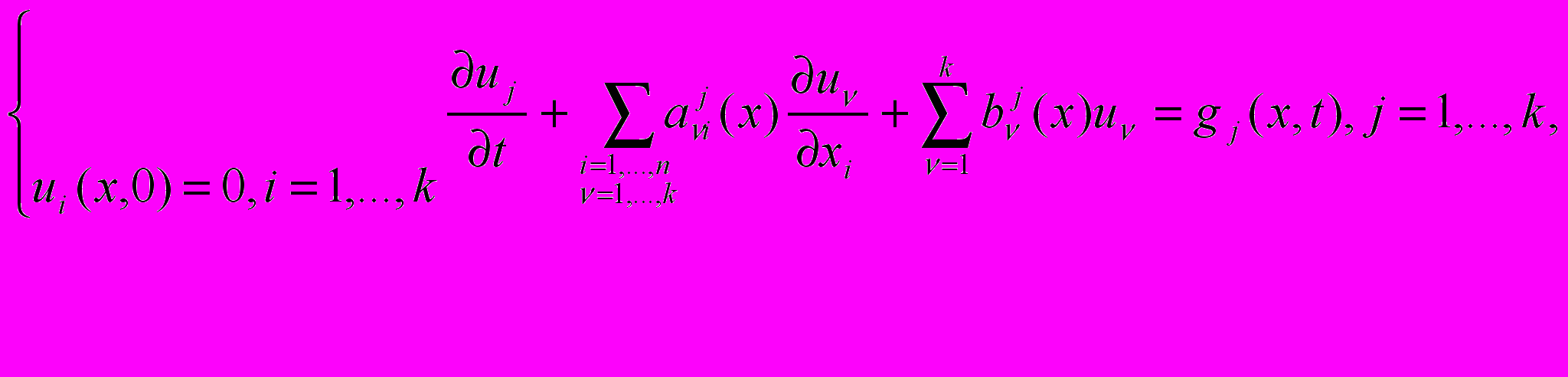
[ Эту же задачу можно сформулировать в матричной форме. Для этого

обозначим



Тогда система запишется в матричной форме:



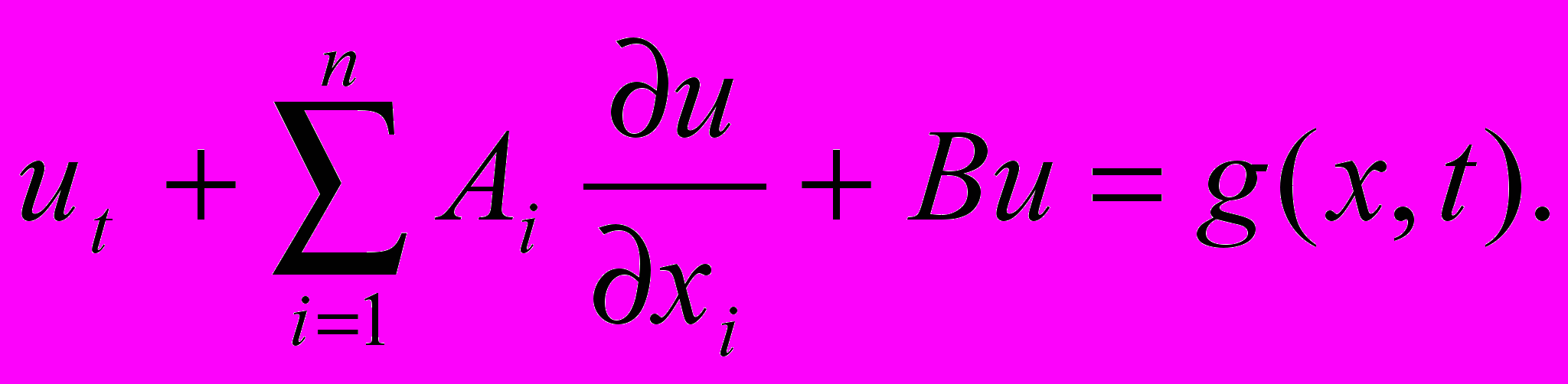
Начальные условия на ui(x, t) перейдут при этом в начальное условие для вектор-функции

u(x, t): u(x, 0)=0].


Литература та же, что в теме 1.

Расширенный вариант лекций по теме 6 и дополнительную литературу можно найти

В Приложении «Ж. Дюамель».