Задача Коши для квазилинейных дифференциальных уравнений в частных производных первого порядка
| Вид материала | Задача |
- Методы современной математики для инженеров, 32.71kb.
- «Математическое моделирование» Общая трудоёмкость дисциплины составляет, 21.97kb.
- Вопросы к экзамену по курсу «Уравнения математической физики» (6 семестр), 55.2kb.
- Программа дисциплины Дифференциальные уравнения Семестр, 29.32kb.
- Уравнения математической физики направление подготовки, 18.02kb.
- Задача Коши для одномерного уравнения Даламбера. Формула Даламбера, 45.74kb.
- А. Ю. Горицкий 1 год, 3 курс, поток механиков Задача, 39.92kb.
- Лекции Число часов, 51.1kb.
- Лекции Число часов, 50.92kb.
- Численное решение обыкновенных дифференциальных уравнений, 10.66kb.
Вопросы по УМФ. (Все, что доказывалось на лекциях — доказывать)
- Гамма-функция Эйлера. Определение, рекуррентное соотношение, формула дополнения.
- Гамма-функция Эйлера. Определение, асимптотика, график.
- Бета-функция и её связь с гамма-функцией.
- Основные и обобщенные функции. Свойства обобщенных функций.
- Примеры обобщенных функций.
- Дельта-функция Дирака и ей свойства.
- Дифференцирование обобщенных функций.
- Дельтообразные последовательности и слабый предел.
- Самосопряженный вид дифференциального уравнения. Задача Штурма-Лиувилля для линейных дифференциальных уравнений второго порядка.
- Свойства собственных функций и собственных значений задачи Штурма-Лиувилля.
- Линейные уравнения в частных производных I порядка. Характеристическая система и ее первые интегралы.
- Задача Коши для квазилинейных дифференциальных уравнений в частных производных первого порядка.
- Классификация уравнений в частных производных второго порядка. Уравнения гиперболического типа.
- Классификация уравнений в частных производных второго порядка. Уравнения параболического типа.
- Классификация уравнений в частных производных второго порядка. Уравнения эллиптического типа
- Физические задачи, приводящие к уравнениям в частных производных. Уравнение колебаний струны.
- Уравнение колебаний струны. Начальные и граничные условия.
- Уравнение колебаний струны. Задача Коши.
- Корректность постановки задач математической физики.
- Задача Коши для одномерного однородного волнового уравнения. Формула Даламбера.
- Задача Коши для одномерного неоднородного волнового уравнения.
- Cмешанная задача для одномерного однородного волнового уравнения.
- Cмешанная задача для одномерного неоднородного волнового уравнения
- Уравнение Бесселя. Функции Бесселя первого рода J (x).
- Функции Бесселя первого рода J (x) и их свойства. Общее решение уравнения Бесселя для n.
- Функции Бесселя второго рода N (x) и их свойства. Общее решение уравнения Бесселя для произвольных .
- Рекуррентные соотношения для функций Бесселя. Функции Бесселя полуцелого индекса.
- Асимптотика и графики функций Бесселя первого и второго рода.
- Модифицированные функции Бесселя первого и второго рода.
- Асимптотика и графики модифицированных функций Бесселя первого и второго рода.
- Задача Штурма—Лиувилля для уравнения Бесселя. (Задача 1).
- Задача Штурма—Лиувилля для уравнения Бесселя. (Задача 2).
- Ряды Фурье—Бесселя и Дини.
- Преобразование Лапласа функций Бесселя. Равенство Парсеваля и частные случаи теоремы Эфроса.
- Уравнения диффузии и теплопроводности. Типы граничных условий.
- Уравнение Лапласа. Основные краевые задачи для уравнения Лапласа.
- Разделение переменных в двумерном уравнении Лапласа в декартовой системе координат (случай непрерывных граничных условий).
- Разделение переменных в двумерном уравнении Лапласа в декартовой системе координат (случай разрывных граничных условий).
- Разделение переменных в двумерном уравнении Лапласа в полярной системе координат.
- Интеграл Пуассона.
- Разделение переменных в уравнении Лапласа в цилиндрической системе координат.
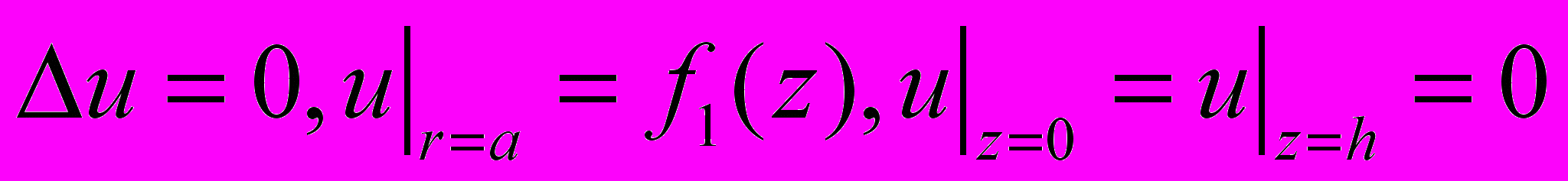
- Разделение переменных в уравнении Лапласа в цилиндрической системе координат.
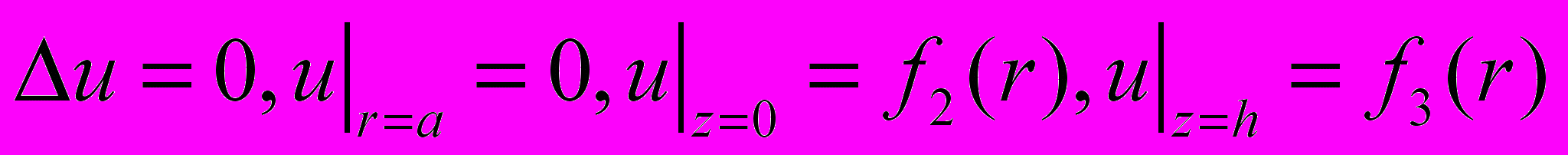
- Полиномы Лежандра. Производящая функция .Формула Родрига. Рекуррентные соотношения для полиномов Лежандра.
- Ортогональность полиномов Лежандра. Задача Штурма-Лиувилля для уравнения Лежандра. Ряд Фурье—Лежандра.
- Присоединенные функции Лежандра. Ряд Фурье по присоединенным функциям Лежандра.
- Сферические функции. Задача Штурма-Лиувилля и соотношение ортогональности.
- Полиномы Эрмита. Производящая функция .Формула Родрига. Рекуррентные соотношения для полиномов Эрмита.
- Ортогональность полиномов Лежандра. Задача Штурма-Лиувилля для уравнения Лежандра. Ряд Фурье—Лежандра.
- Ортогональность полиномов Эрмита. Задача Штурма-Лиувилля для уравнения Эрмита. Ряд Фурье—Эрмита.
- Функции Эрмита.
- Полиномы Лагерра. Производящая функция и формула Родрига. Рекуррентные соотношения для полиномов Лагерра .
- Ортогональность полиномов Лагерра. Ряд Фурье-Лагерра.
- Линейный гармонический осциллятор.
