Вопросы к экзамену по учебной дисциплине «Дифференциальные уравнения»
| Вид материала | Вопросы к экзамену |
- Дифференциальные уравнения (вопросы к экзамену), 26.43kb.
- Вопросы к экзамену по курсу «Дифференциальные уравнения», 22.85kb.
- Программа-минимум кандидатского экзамена по специальности 01. 01. 02 «Дифференциальные, 37.38kb.
- Календарный план чтения лекций, 27.51kb.
- Обыкновенные дифференциальные уравнения, 17.54kb.
- Рабочая программа. Тематический план. Темы семинарских занятий. Контрольные вопросы, 127.79kb.
- Уравнения математической физики направление подготовки, 18.02kb.
- Вопросы к экзамену по дифференциальным уравнениям, 21.14kb.
- Учебной дисциплины «Обыкновенные дифференциальные уравнения» для направления подготовки, 18.38kb.
- Л. С. Понтрягин Обыкновенные дифференциальные уравнения М., «Наука», 1974, 31.21kb.
Вопросы к экзамену по учебной дисциплине
«Дифференциальные уравнения», 3 семестр
- Определение дифференциального уравнения и решения дифференциального уравнения. Задача Коши и краевая задача.
- Геометрическое истолкование дифференциального уравнения (векторное поле) и его решения (интегральная кривая).
- Задача обратная решению дифференциального уравнения.
- Уравнения в полных дифференциалах.
- Линейные уравнения первого порядка.
- Уравнения с разделяющимися переменными и однородные уравнения первого порядка.
- Комплексная функция. Нормальная система дифференциальных уравнений. Расщепление комплексной системы на систему действительных уравнений.
- Теорема существования и единственности (формулировка). Теорема существования и единственности для уравнения n-го порядка (формулировка).
- Экспонента комплексного числа, свойства.
- Некоторые сведения о линейных дифференциальных уравнениях, свойства решений (с доказательством).
- Линейные однородные уравнения с постоянными коэффициентами. Определение оператора
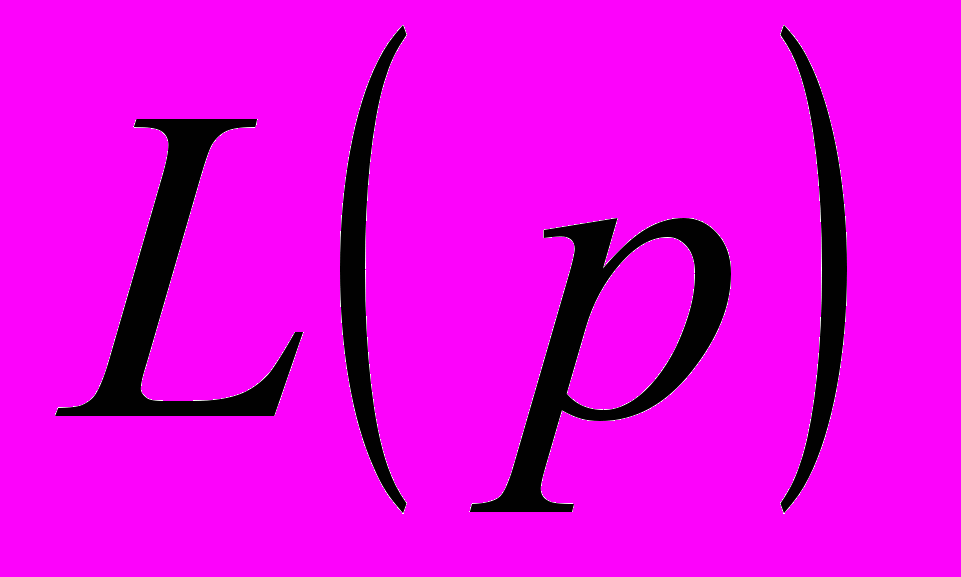, его свойства. Доказательство формулы: 
.
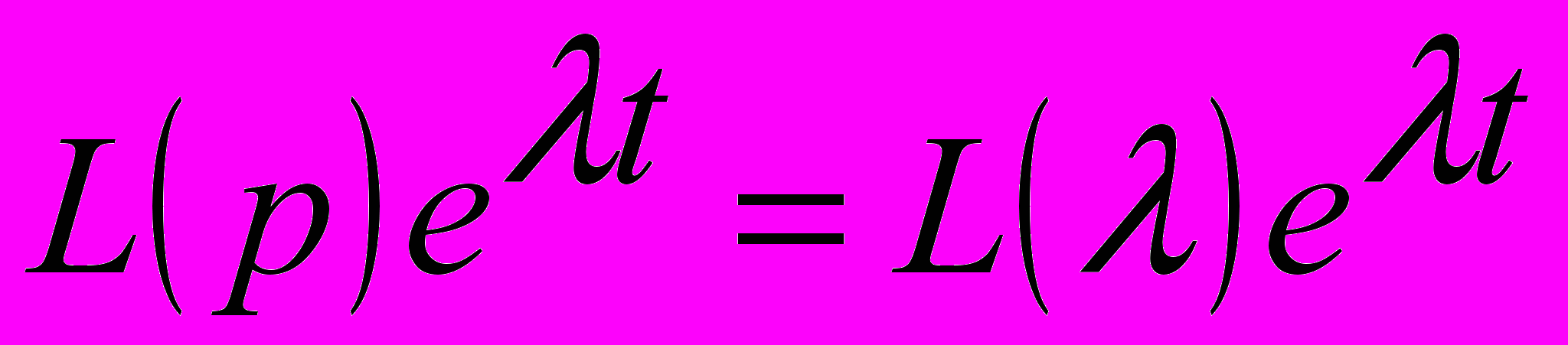- Линейные однородные уравнения с постоянными коэффициентами (случай простых корней). Теорема о виде решения.
- Линейные однородные уравнения с постоянными коэффициентами (случай простых корней). Действительное решение уравнения с действительными коэффициентами.
- Линейные однородные уравнения с постоянными коэффициентами (случай кратных корней). Формула смещения. Предложение о семействе функций
.
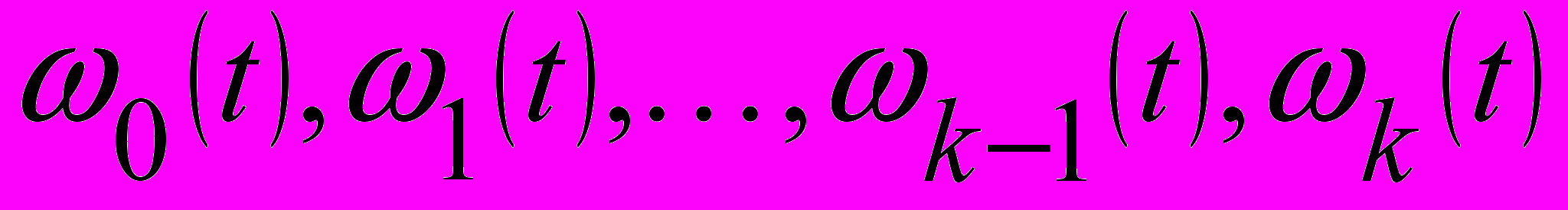- Линейные однородные уравнения с постоянными коэффициентами (случай кратных корней). Теорема о виде решения.
- Линейные неоднородные уравнения с постоянными коэффициентами. Вид решения. Определение квазимногочлена. Теорема о виде частного решения.
- Линейные неоднородные уравнения с постоянными коэффициентами. Свойство квазимногочленов.
- Нормальная линейная однородная система с постоянными коэффициентами. Случай простых корней характеристического уравнения.
- Нормальная линейная однородная система с постоянными коэффициентами. Общий случай.
- Нормальная система линейных уравнений с переменными коэффициентами. Простейшие свойства решений однородной системы. Линейная зависимость системы решений.
- Нормальная система линейных уравнений с переменными коэффициентами. Фундаментальная система решений. Её существование, выражение решения с помощью фундаментальной системы решений.
- Нормальная система линейных уравнений с переменными коэффициентами. Детерминант Вронского. Соответствие между произвольной матрицей с ненулевым определителем и фундаментальной матрицей линейной системы.
- Нормальная система линейных уравнений с переменными коэффициентами. Правило дифференцирования детерминанта. Формула Лиувилля.
- Нормальная неоднородная система линейных уравнений с переменными коэффициентами. Вид решения. Метод вариации постоянных.
- Линейные уравнения n-го порядка с переменными коэффициентами. Сведение к нормальной линейной системе. Эквивалентность решения уравнения и системы.
- Линейные уравнения n-го порядка с переменными коэффициентами. Линейная независимость. Фундаментальная система решений. Её существование, выражение решения с помощью фундаментальной системы решений.
- Линейные уравнения n-го порядка с переменными коэффициентами. Детерминант Вронского. Формула Лиувилля.
- Линейные уравнения n-го порядка с переменными коэффициентами. Метод вариации постоянных.
- Показательная функция матрицы. Ряд от матрицы.
- Экспонента матрицы. Свойства и способы ее нахождения.
- Экспонента диагональной и жордановой матрицы.
- Линейные уравнения второго порядка. Приведение к виду без первой производной.
- Понятия колеблющегося и неколеблющегося на интервале решения. Теорема о неколеблющемся решении.
- Теорема Штурма и ее следствие.
- Теорема сравнения и ее следствие.
- Теорема Кнезера. Способы задания краевых условий для линейных уравнений 2-го порядка.
- Теорема существования и единственности решения задачи Коши для нормальной системы линейных уравнений. Формулировка теоремы существования и единственности решения задачи Коши для линейного уравнения n-го порядка.
- Теорема существования и единственности решения задачи Коши для одного уравнения. Ломаные Эйлера.
- Теорема существования и единственности решения задачи Коши для нормальной системы дифференциальных уравнений.
Лектор__________________ доцент кафедры ТУиО, к. ф.-м. н. Алеева С.Р.