Geum.ru

Рабочая программа. Тематический план. Темы семинарских занятий. Контрольные вопросы к коллоквиумам. Контрольные вопросы к экзамену

Вид материалаРабочая программа

Содержание


Цели и задачи курса
Рабочая программа
Номер раздела
Тематический план
Подобный материал:
Специальность 010100 «математика»


Дифференциальные уравнения


Требования ГОСТ к содержанию курса.

Цели и задачи курса.

Рабочая программа.

Тематический план.

Темы семинарских занятий.

Контрольные вопросы к коллоквиумам.

Контрольные вопросы к экзамену.

Дополнительная информация.

Литература.


Требования ГОСТ к содержанию курса


Математик должен быть подготовлен к выполнению деятельности в областях, использующих математические методы и компьютерные технологии; созданию и использованию математических моделей процессов и объектов; разработке эффективных математических методов решения задач естествознания, техники, экономики и управления. Успешное усвоение курса «дифференциальные уравнения» является одним из главных условий для достижения этих целей.


^ Цели и задачи курса


Дифференциальные уравнения возникают в процессе математического моделирования какого-либо процесса или явления. Математическое моделирование, как известно, есть метод познания окружающего мира, прогнозирования и управления. Поэтому представление о дифференциальных моделях, знание их основных типов необходимо для качественного образования студента-математика. Основными целями курса можно считать следующие:
  1. обеспечить овладение минимумом знаний и практических навыков по методам решения обыкновенных дифференциальных уравнений, с тем, чтобы по мере необходимости студенты могли использовать их для самостоятельной исследовательской работы;
  2. познакомить студентов с простейшими приемами и методами качественного исследования обыкновенных дифференциальных уравнений;
  3. продемонстрировать возможности современных пакетов символьной математики в точном и приближенном решении различных дифференциальных уравнений и систем;
  4. сравнить аналитический и «машинный» подходы к решению той или иной задачи, выявить их сильные и слабые стороны.


^ Рабочая программа


Составлена доцентом Мачулисом В.В.,

утверждена на заседании кафедры

математического моделирования _______


Программа рассчитана на 68 лекционных и 68 практических часов. Курс изучается в течение 3 - го и 4 - го семестра обучения. За это время проводится три коллоквиума, в конце года сдается экзамен.


^ Номер раздела
Содержание раздела
Лекции
Практические

занятия

1
Понятие о дифференциальном уравнении
4
4

2
Элементарные приемы интегрирования
10
12

3
Задача Коши
4
4

4
Уравнения, не разрешенные относительно производной
8
6







Коллоквиум №1
Контрольная работа №1

5
Уравнения порядка выше первого
8
4

6
Методы решения уравнений порядка выше первого
8
10







Коллоквиум №2
Домашняя контрольная работа (№2)

7
Матричный метод решения систем
8
10

8
Теория устойчивости
10
8

9
Некоторые приложения теории дифференциальных уравнений
8
10







Коллоквиум №3
Контрольная работа №3


^ Тематический план


1. Понятие о дифференциальном уравнении и его общем и частном решении, поле направлений, семействе интегральных кривых.

2. Элементарные приемы интегрирования: уравнения с разделяющимися переменными, однородные и линейные уравнения первого порядка, уравнение Бернулли, уравнения в полных дифференциалах и с интегрирующим множителем.

3. Задача Коши, теорема существования и единственности решения задачи Коши.

4. Уравнения, не разрешенные относительно производной, общий метод введения параметра, уравнения Лагранжа и Клеро, особые решения и их нахождение.

5. Уравнения порядка выше первого. Линейная зависимость функций и определитель Вронского, формула Остроградского-Лиувилля, фундаментальные системы решений и общее решение линейного однородного уравнения (системы), неоднородные линейные уравнения (системы).

6. Методы решения линейных неоднородных уравнений (систем): метод вариации произвольных постоянных и метод неопределенных коэффициентов.

7. Матричный метод решения однородных систем: матричная запись системы, характеристические числа и элементарные делители, преобразование подобия, матричная экспонента, интегральная матрица.

8. Непрерывная зависимость решения от параметра и начальных данных. Устойчивость по Ляпунову, теорема Ляпунова об устойчивости по первому приближению и ее применение, фазовые траектории автономной двумерной системы, особые точки фазовой плоскости, качественная эквивалентность систем дифференциальных уравнений.

9. Некоторые приложения теории дифференциальных уравнений: малый коэффициент при старшей производной, асимптотическое поведение решений при больших x, осцилляция решений дифференциальных уравнений.


Темы семинарских занятий

  1. Основные методы интегрирования (повторение).
  2. Составление дифференциальных уравнений семейств кривых.
  3. Уравнения с разделяющимися переменными.
  4. Задачи на составление простейших дифференциальных уравнений.
  5. Однородные уравнения и приводящиеся к ним.
  6. Линейные уравнения первого порядка (и уравнение Бернулли).
  7. Уравнения в полных дифференциалах.
  8. Уравнения с интегрирующим множителем.
  9. Существование и единственность решения.
  10. Уравнения, не разрешенные относительно производной.
  11. Уравнения Лагранжа и Клеро. Особые решения.
  12. Уравнения, допускающие понижение порядка.
  13. Контрольная работа №1.
  14. Линейные однородные уравнения с постоянными коэффициентами.
  15. Линейные неоднородные уравнения с постоянными коэффициентами. Метод вариации произвольных постоянных.
  16. Линейные неоднородные уравнения с постоянными коэффициентами. Метод неопределенных коэффициентов.
  17. Задачи, приводящиеся к линейным неоднородным уравнениям.
  18. Линейные системы с постоянными коэффициентами.
  19. Элементарные делители матриц. Матричная экспонента.
  20. Матричный метод решения систем.
  21. Устойчивость решений уравнений.
  22. Устойчивость по первому приближению.
  23. Критерии устойчивости.
  24. Фазовая плоскость. Особые точки. Качественная эквивалентность линейных и нелинейных систем.
  25. Некоторые приложения теории дифференциальных уравнений. Малый параметр при старшей производной.
  26. Контрольная работа №3.


Вопросы к коллоквиумам


Коллоквиум №1. Уравнения первого порядка.

  1. Понятие об обыкновенном дифференциальном уравнении.
  2. Геометрическая интерпретация дифференциального уравнения и его решений. Поле направлений. Семейство интегральных кривых.
  3. Уравнения первого порядка с разделяющимися переменными.
  4. Однородные уравнения первого порядка и приводящиеся к ним.
  5. Геометрическое свойство интегральных кривых однородного уравнения первого порядка.
  6. Линейные уравнения первого порядка. Метод вариации произвольной постоянной.
  7. Линейные уравнения первого порядка. Метод Бернулли.
  8. Уравнение Бернулли и метод его решения.
  9. Геометрическое свойство интегральных кривых линейного уравнения первого порядка.
  10. Уравнение в полных дифференциалах.
  11. Уравнение с интегрирующим множителем. Интегрирующий множитель линейного уравнения.
  12. Принцип сжимающих отображений.
  13. Задача Коши. Теорема существования и единственности решения дифференциального уравнения вида .
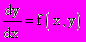  14. Интегрирующий множитель и особые решения.
  15. Некоторые приближенные способы решения уравнений (способ Эйлера-Коши и применение степенных рядов).
  16. Уравнения, не разрешенные относительно производной (некоторые частные случаи).
  17. Уравнения, не разрешенные относительно производной. Общий метод введения параметра.
  18. Уравнения Лагранжа и Клеро. Особые решения.
  19. Теорема существования и единственности для уравнений, не разрешенных относительно производной.
  20. Нахождение особых решений.


Коллоквиум №2. Уравнения порядка выше первого и системы уравнений.

  1. Уравнения порядка выше первого (начальные понятия и геометрическая интерпретация).
  2. Некоторые способы понижения порядка.
  3. Общие свойства линейных уравнений высших порядков.
  4. Однородное линейное уравнение n - го порядка.
  5. Линейная зависимость и независимость системы функций.
  6. Вронскиан и его свойства.
  7. Формула Остроградского - Лиувилля.
  8. Фундаментальная система и общее решение однородного линейного уравнения n - го порядка.
  9. Общее решение неоднородного линейного уравнения n - го порядка.
  10. Построение фундаментальной системы решений однородного линейного уравнения с постоянными коэффициентами.
  11. Общее решение линейного неоднородного уравнения n - го порядка с постоянными коэффициентами и его нахождение методом вариации произвольных постоянных.
  12. Системы дифференциальных уравнений (общие понятия).
  13. Решение системы дифференциальных уравнений путем сведения к одному уравнению более высокого порядка.
  14. Метод интегрируемых комбинаций.
  15. Системы линейных дифференциальных уравнений.
  16. Системы линейных дифференциальных уравнений с постоянными коэффициентами.


Коллоквиум №3. Матричный метод решения систем. Теория устойчивости.

  1. Характеристические числа и элементарные делители.
  2. Матричная экспонента.
  3. Матричная запись линейной однородной системы.
  4. Интегрирование однородной линейной системы с постоянными коэффициентами.
  5. Линейные однородные системы второго порядка.
  6. Линейные однородные системы третьего порядка.
  7. Основные понятия теории устойчивости.
  8. Фазовые портреты автономных систем на плоскости. Простейшие типы точек покоя.
  9. Исследование на устойчивость по первому приближению.
  10. Понятие о качественной эквивалентности систем дифференциальных уравнений на плоскости.
  11. Критерий Рауса - Гурвица.
  12. Критерий Михайлова.
  13. Непрерывная зависимость решения от параметра и начальных данных.
  14. Малый параметр при старшей производной.
  15. Асимптотическое поведение решений при больших x.
  16. Осцилляция решений дифференциальных уравнений.


Вопросы к экзамену

  1. Понятие об обыкновенном дифференциальном уравнении.
  2. Геометрическая интерпретация дифференциального уравнения и его решений. Поле направлений. Семейство интегральных кривых.
  3. Уравнения первого порядка с разделяющимися переменными.
  4. Однородные уравнения первого порядка и приводящиеся к ним.
  5. Геометрическое свойство интегральных кривых однородного уравнения первого порядка.
  6. Линейные уравнения первого порядка. Метод вариации произвольной постоянной.
  7. Линейные уравнения первого порядка. Метод Бернулли.
  8. Уравнение Бернулли и метод его решения.
  9. Геометрическое свойство интегральных кривых линейного уравнения первого порядка.
  10. Уравнение в полных дифференциалах.
  11. Уравнение с интегрирующим множителем. Интегрирующий множитель линейного уравнения.
  12. Принцип сжимающих отображений.
  13. Задача Коши. Теорема существования и единственности решения дифференциального уравнения вида .
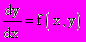  14. Интегрирующий множитель и особые решения.
  15. Некоторые приближенные способы решения уравнений (способ Эйлера-Коши и применение степенных рядов).
  16. Уравнения, не разрешенные относительно производной (некоторые частные случаи).
  17. Уравнения, не разрешенные относительно производной. Общий метод введения параметра.
  18. Уравнения Лагранжа и Клеро. Особые решения.
  19. Теорема существования и единственности для уравнений, не разрешенных относительно производной.
  20. Нахождение особых решений.
  21. Уравнения порядка выше первого (начальные понятия и геометрическая интерпретация).
  22. Некоторые способы понижения порядка.
  23. Общие свойства линейных уравнений высших порядков.
  24. Однородное линейное уравнение n - го порядка.
  25. Линейная зависимость и независимость системы функций.
  26. Вронскиан и его свойства.
  27. Формула Остроградского - Лиувилля.
  28. Фундаментальная система и общее решение однородного линейного уравнения n - го порядка.
  29. Общее решение неоднородного линейного уравнения n - го порядка.
  30. Построение фундаментальной системы решений однородного линейного уравнения с постоянными коэффициентами.
  31. Общее решение линейного неоднородного уравнения n - го порядка с постоянными коэффициентами и его нахождение методом вариации произвольных постоянных.
  32. Системы дифференциальных уравнений (общие понятия).
  33. Решение системы дифференциальных уравнений путем сведения к одному уравнению более высокого порядка.
  34. Метод интегрируемых комбинаций.
  35. Системы линейных дифференциальных уравнений.
  36. Системы линейных дифференциальных уравнений с постоянными коэффициентами.
  37. Характеристические числа и элементарные делители.
  38. Матричная экспонента.
  39. Матричная запись линейной однородной системы.
  40. Интегрирование однородной линейной системы с постоянными коэффициентами.
  41. Линейные однородные системы второго порядка.
  42. Линейные однородные системы третьего порядка.
  43. Основные понятия теории устойчивости.
  44. Фазовые портреты автономных систем на плоскости. Простейшие типы точек покоя.
  45. Исследование на устойчивость по первому приближению.
  46. Понятие о качественной эквивалентности систем дифференциальных уравнений на плоскости.
  47. Критерий Рауса - Гурвица.
  48. Критерий Михайлова.
  49. Непрерывная зависимость решения от параметра и начальных данных.
  50. Малый параметр при старшей производной.
  51. Асимптотическое поведение решений при больших x.
  52. Осцилляция решений дифференциальных уравнений.


Дополнительная информация


Во время изучения курса дифференциальных уравнений на лекциях и практических занятиях используется система символьной математики Maple V R4 (Waterloo Maple Inc.). Maple V является лидером среди систем компьютерной алгебры; она позволяет решать большое число сложных математических задач из многих разделов математики, в том числе и дифференциальных уравнений. Результаты решения представляются в символьном (аналитическом), численном и графическом виде. Цели применения Maple V в курсе дифференциальных уравнений следующие:
  • дать представление о возможностях применения современных систем компьютерной алгебры (на примере Maple);
  • подготовить студентов к последующему использованию подобных систем в исследовательской работе;
  • продемонстрировать некоторые численные методы решения дифференциальных уравнений и систем с помощью Maple V.

Лекции и практические занятия по курсу проводятся в малом лекционном зале факультета математики и компьютерных наук, оборудованным компьютером и телевизором с большим экраном.


Литература

  1. Агафонов С.А., Герман А.Д., Муратова Т.В. Дифференциальные уравнения. - М.: Издательство МГТУ имени Н.Э. Баумана, 2000.
  2. Амелькин В.В. Дифференциальные уравнения в приложениях. - М.: Наука, 1987.
  3. Краснов М.Л. Обыкновенные дифференциальные уравнения: Учеб. Пособие для вузов. - М.: Высшая школа, 1983.
  4. Матвеев Н.М. Методы интегрирования обыкновенных дифференциальных уравнений. - М.: Высшая школа, 1967.
  5. Матвеев Н.М. Сборник задач и упражнений по обыкновенным дифференциальным уравнениям. - Минск.: Вышэйшая школа, 1977.
  6. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. - Москва - Ленинград.: Государственное издательство технико-теоретической литературы, 1952.
  7. Пономаренко А.К., Сахаров В.Ю., Степанова Т.В., Черняев П.К. Учебные и контрольные задания по обыкновенным дифференциальным уравнениям. - Издательство С.-Петербургского университета, 2000.
  8. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. - М.: Наука. Физматлит, 1998.
  9. Филиппов А.Ф. Сборник задач по дифференциальным уравнениям. - М.: Наука, 1985.
  10. Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. - М.: Наука, 1969.
  11. Дьяконов В.П. Математическая система Maple V R3/R4/R5. М.: «Солон», 1998. 400 с.
  12. Дьяконов В.П. Компьютерная математика. Теория и практика. М.: Нолидж. 1999 г.: «Нолидж», 2001.
  13. Манзон Б.В. Maple V Power Edition. М.: Информац. - издат. дом «Филин», 1998. 240 с.
  14. Матросов А.В. Maple 6. Решение задач высшей математики и механики. - СПб.: БХВ-Петербург, 2001.