Давид Абрамович Шапиро программа

Вид материала

Содержание

Уравнения второго порядка
Специальные функции
Асимптотические методы
Задания ЗАДАНИЕ № 1 (сдать до 25 октября) Вычислить exp(a+bσ
R температура осциллирует как T(t)=T

Подобный материал:

МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ

5 семестр

профессор Давид Абрамович Шапиро

Программа лекций

Уравнения первого порядка

Метод характеристик для линейных и квазилинейных уравнений с частными производными. Задача Коши. Образование разрывов. Характеристики нелинейного уравнения.

Понятие характеристик для систем линейных и квазилинейных уравнений с двумя переменными. Классификация по типам: гиперболические, эллиптические, параболические системы.

Приведение гиперболической системы к каноническому виду. Инварианты Римана, простая волна Римана.

Метод годографа для уравнений газовой динамики. Точные решения для политропного газа.

^ Уравнения второго порядка

Волновое уравнение. Вывод из уравнений Максвелла и газодинамики. Решение одномерного волнового уравнения, формула Даламбера.

Приведение гиперболического, эллиптического и параболического уравнения с двумя переменными к каноническому виду.

Приведение многомерных уравнений к каноническому виду. Классификация по типам. Характеристики гиперболического уравнения, характеристические нормали и их физический смысл.

Понятие автомодельности. Автомодельные подстановки для уравнений теплопроводности.

Разделение переменных. Метод Фурье для гиперболических и параболических уравнений.

^ Специальные функции

Разделение переменных в задаче о колебаниях круглой мембраны. Функции Бесселя.

Разделение переменных в уравнении Шрёдингера для частицы в центрально-симметричном поле. Присоединенные функции Лежандра. Сферические гармоники. Функции Бесселя с полуцелым индексом.

Разложение решения обыкновенного дифференциального уравнения второго порядка вблизи обыкновенной точки и регулярной особой точки. Характеристические показатели.

Гипергеометрическая функция Гаусса и вырожденная гипергеометрическая функция.

Уравнение Шрёдингера для осциллятора и атома водорода. Полиномы Эрмита и Лагерра.

^ Асимптотические методы

Асимптотика интегралов Интеграл Лапласа.

а) Случаи стационарной точки на границе и внутри отрезка интегрирования. Асимптотика Γ–функции Эйлера.

б) Метод стационарной фазы. Асимптотика функции Бесселя.

в) Метод перевала. Асимптотика функций Лежандра и Эйри.

Метод усреднения. Асимптотика усредненного решения дифференциального уравнения.

Литература

В. Я. Арсенин. Методы математической физики и специальные функции. М.: Наука, 1984.
С. К. Годунов. Уравнения математической физики. М.: Наука, 1971.
Задачи по математическим методам физики. Ч. I, II. Новосибирск: НГУ, 1994.
Л. Д. Ландау, Е. М. Лифшиц. Квантовая механика; Гидродинамика.
Дж. Мэтьюз, Д. Уокер. Математические методы в физике. М.: Атомиздат, 1972.
Ф. Олвер. Асимптотика и специальные функции. М.: Наука, 1990.

Дополнительная литература

В. И. Арнольд. Дополнительные главы теории обыкновенных дифференциальных уравнений. М.: Наука, 1978. — § 7; Обыкновенные дифференциальные уравнения. — Изд. 3^e. М.: Наука, 1984. — § 11.
А. Найфэ. Введение в методы возмущений. М.: Мир, 1984.
Р. Рихтмайер. Принципы современной математической физики. М.: Мир, Т.1 — 1982.
Ю. В. Сидоров, М. В. Федорюк, М. И. Шабунин. Лекции по теории функций комплексного переменного. М.: Наука, 1976. — Гл.VII.

Программа семинаров

доцент Евгений Вадимович Подивилов

Унитарные и эрмитовы матрицы, проекторы. Матрицы Паули.
Собственные значения. Функции от матриц. Резольвента.
Ортогонализация. Полнота системы функций. Проверка самосопряженности дифференциальных операторов. Свойства -функции.
Линейные уравнения первого порядка. Характеристики.
Квазилинейные уравнения. Опрокидывание.
Характеристики нелинейных уравнений. Общее решение уравнения Гамильтона – Якоби.
Системы линейных уравнений. Приведение к каноническому виду.
Инварианты Римана и характеристики в случае двух переменных.
Задача о политропном газе. Простая волна Римана.
Характеристические переменные. Области эллиптичности и гиперболичности. Приведение уравнений второго порядка к каноническому виду.
Исключение первых производных. Волновое уравнение. Формула Даламбера.
Поиск автомодельной подстановки с помощью масштабных преобразований. Автомодельные решения линейного и нелинейного уравнения теплопроводности.
Решения нелинейных уравнений типа бегущей волны. Солитоны.
Решение задач о колебаниях струны методом Фурье.
Решение уравнений теплопроводности и Лапласа методом Фурье.
Разделение переменных уравнения Шрёдингера в ортогональных системах координат.
Сферические гармоники. Полиномы Лежандра и Эрмита. Основные свойства функции Бесселя: разложение, рекуррентные соотношения, производящая функция, интегральное представление, соотношение ортогональности.
Характеристические показатели в особых точках. Определяющее уравнение. Гипергеометрические функции.
Асимптотика интеграла Лапласа. Метод стационарной фазы.
Метод перевала. Асимптотика функции Эйри.
Метод усреднения. Преобразование Боголюбова – Крылова.

Контрольная работа: проводится по группам перед началом контрольной недели.

Коллоквиум: проводится после окончания контрольной недели.

^ Задания

ЗАДАНИЕ № 1 (сдать до 25 октября)

Вычислить exp(a+bσ), где σ – матрицы Паули, a и b комплексные скаляр и вектор.
Найти решение кинетического уравнения

в скрещенных электрическом и магнитном полях E H=0. Как выглядят

характеристики?

Найти закон колебаний холодного электронного газа относительно однородного неподвижного ионного фона плотности n₀. Колебания описываются уравнением непрерывности для плотности электронов n(x,t), уравнением Эйлера для их скорости u(x,t) и уравнением Пуассона для электрического поля E(x,t) .

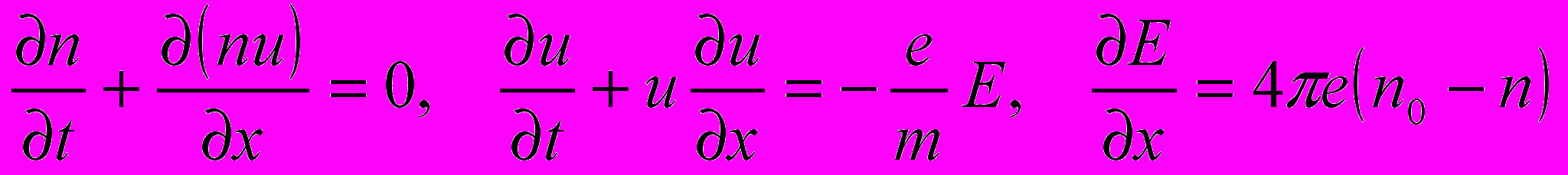При каких начальных значениях амплитуды электрического поля E₀ происходит опрокидывание, если u(x,0)=0,

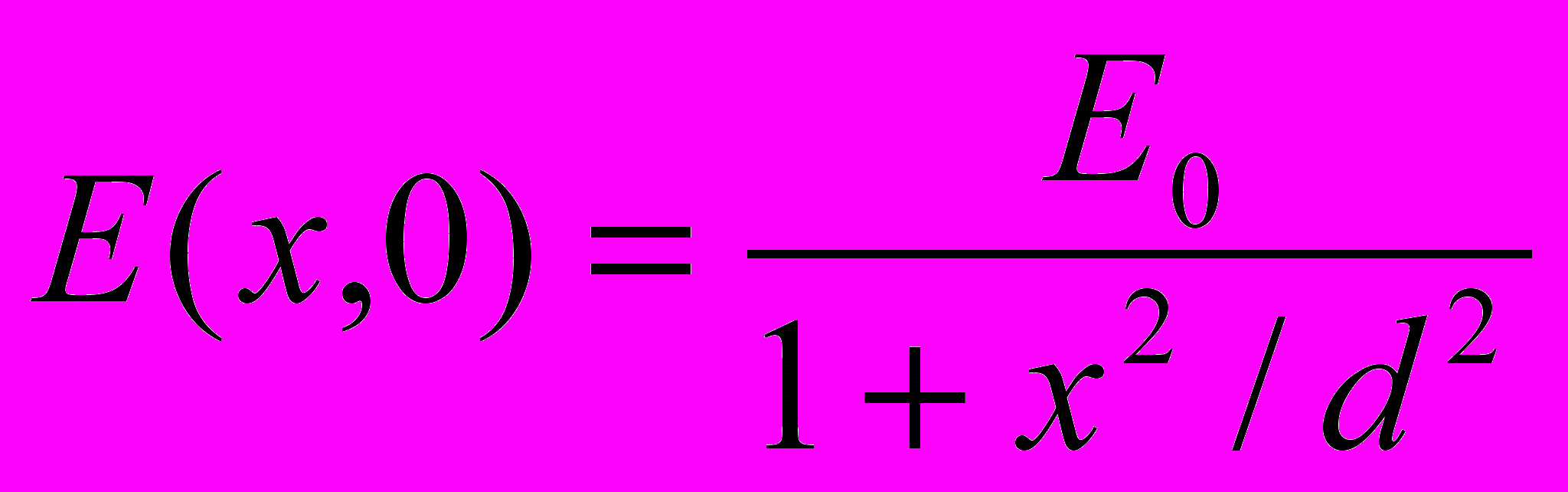Решить уравнение Гамильтона–Якоби с начальным условием .

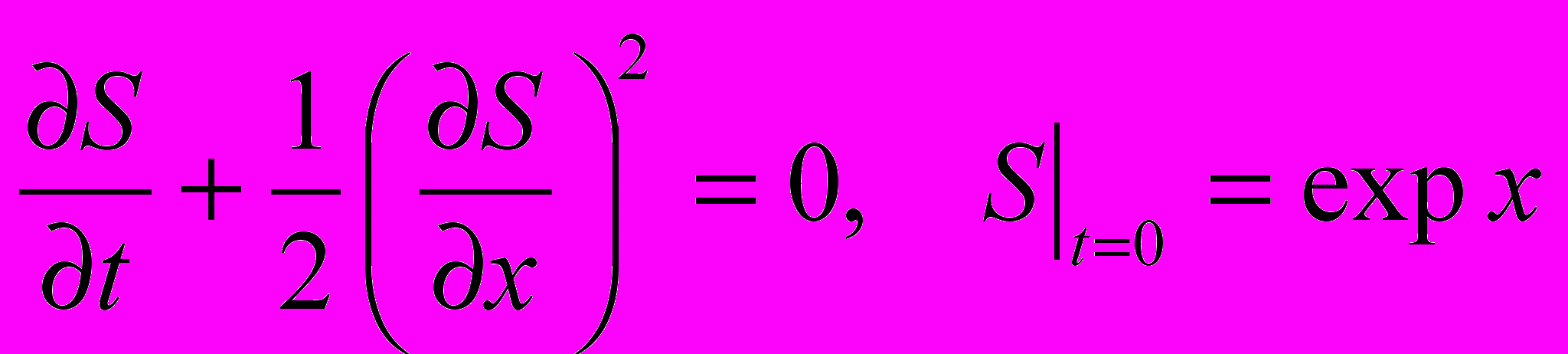ЗАДАНИЕ № 2 (сдать до 25 ноября)

Найти общее решение уравнения .
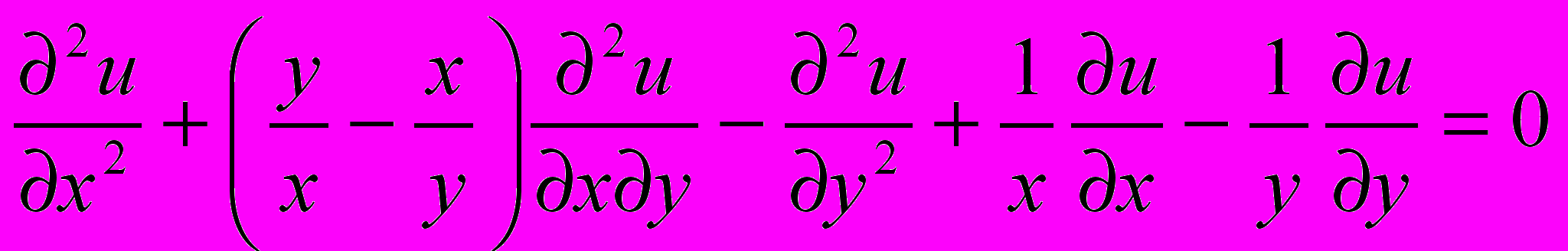Струна длины l с закрепленными концами в начальный момент имеет форму полуокружности 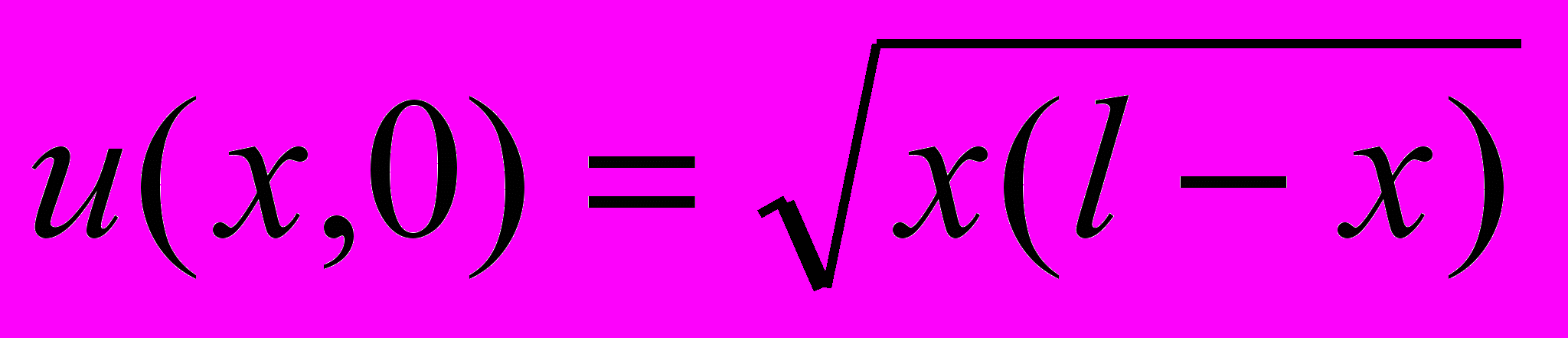и нулевую скорость. Найти зависимость смещения от координат и времени.
На границе бесконечного цилиндра радиуса ^ R температура осциллирует как T(t)=T₀ sin ωt. Найти распределение температуры в цилиндре как функцию времени. Исследовать решение при ω>>χ /R², где χ – температуропроводность.
Найти собственные частоты ω колебаний шара радиуса R 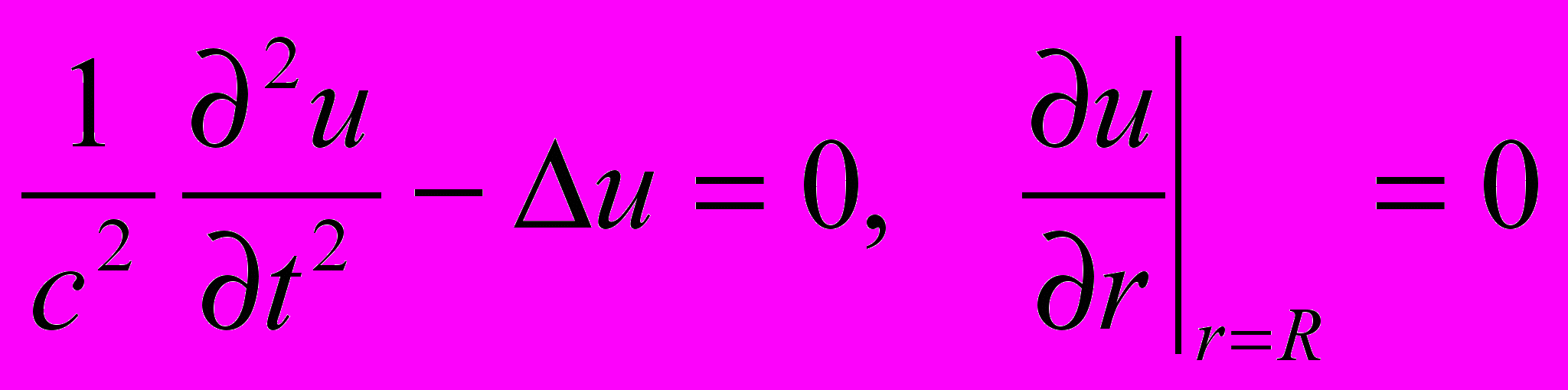при условии ωR/c>>1.

ЗАДАНИЕ № 3 (сдать до 25 декабря)

Вычислить асимптотику интеграла 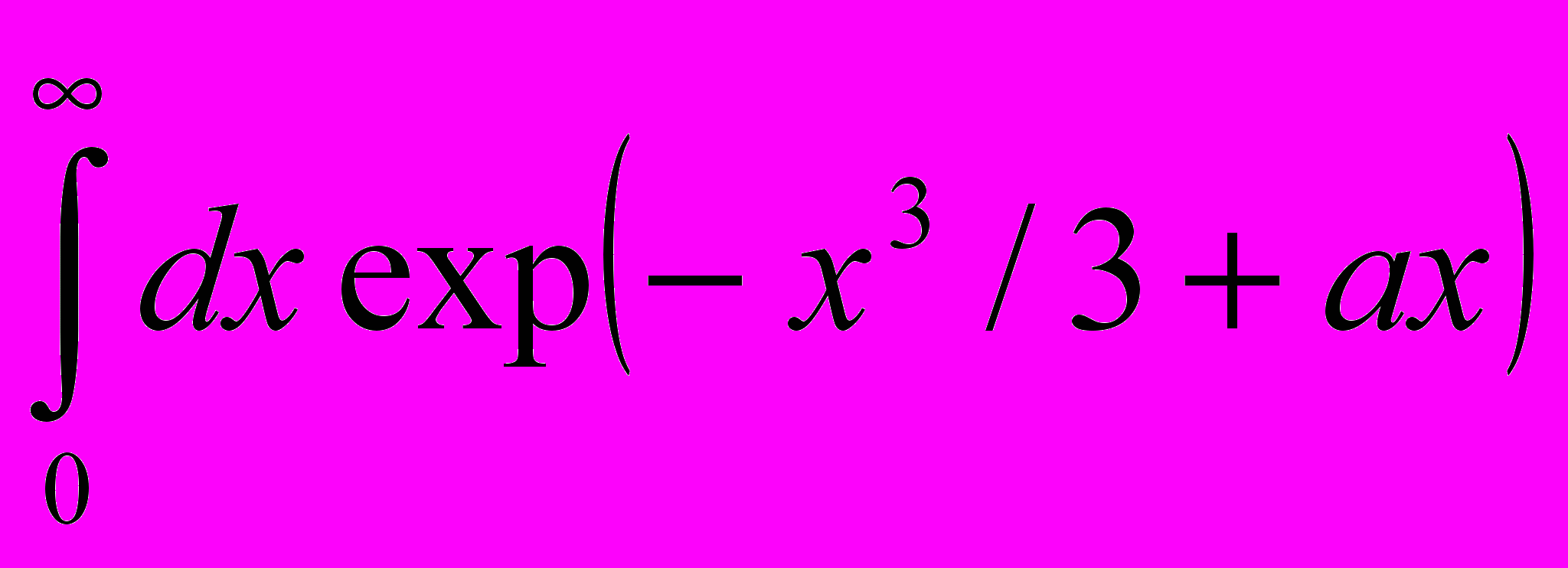, где a – комплексный параметр, |a|→∞.
Найти решение ψ(x,t) уравнения Шрёдингера

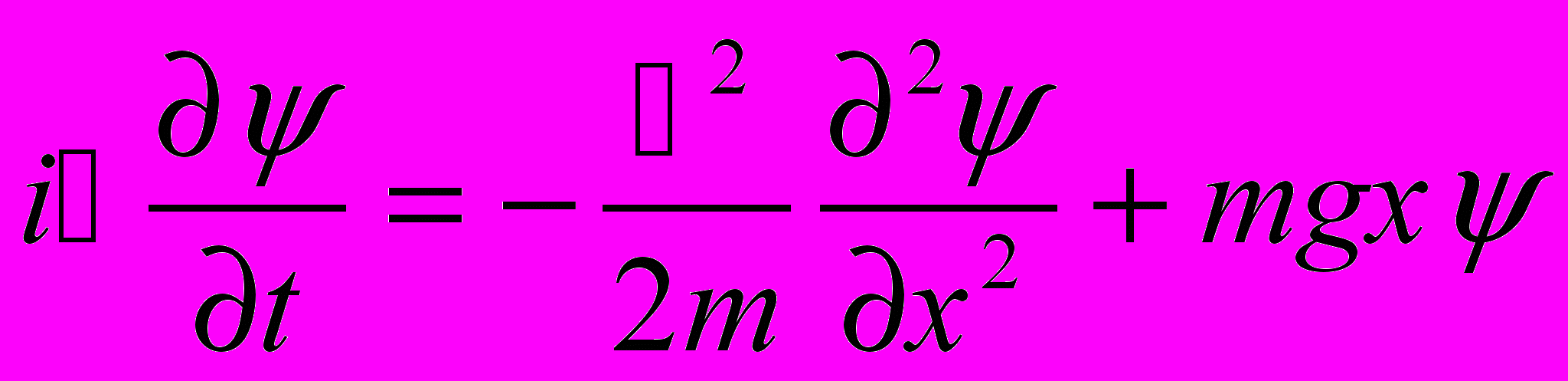
с начальным условием ψ(x,0)=A exp(-|x|/a). Исследовать асимптотику на больших временах. С какой скоростью движется центр пакета и как меняется его ширина?

Найти методом усреднения эволюцию колебаний маятника, испытывающего трение при прохождении точки x=a:

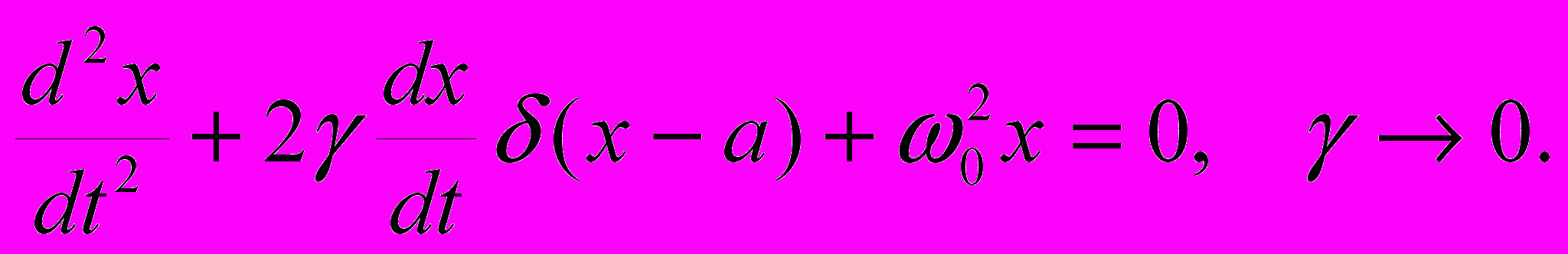
Сравнить с точным решением.