Экзаменационные вопросы по курсу «Высшая математика, часть 6» для студентов второго курса фсап заочной формы обучения
| Вид материала | Экзаменационные вопросы |
- Контрольная работа по курсу «Высшая математика (раздел «Математическое программирование»)», 24.35kb.
- Программа курса, методические указания по выполнению контрольных работ, планы семинарских, 462.04kb.
- Экзаменационные вопросы по курсу «Исследование социально-экономических и политических, 21.31kb.
- Методические рекомендации для студентов очно-заочной и заочной форм обучения Тематика, 268.03kb.
- Темы курсовой работы и экзаменационные вопросы по дисциплине: «Экономика отрасли» для, 31.96kb.
- Методические рекомендации к выполнению курсовой работы по основам менеджмента для студентов, 236.14kb.
- Программа, методические указания и контрольные задания по курсу «основы программирования, 516.11kb.
- Темы контрольных работ по курсу «Религиозная философия» Ч. для студентов 3 курса заочной, 27.42kb.
- Тематический план курса для студентов очно-заочной формы обучения 7 > Тематический, 1325.78kb.
- Методические указания и контрольные задания для студентов 1 курса железнодорожных специальностей, 785.04kb.
Экзаменационные вопросы по курсу
«Высшая математика, часть 6»
для студентов второго курса ФСАП заочной формы обучения.
(3 семестр)
Лектор: доц. Афанасьева О.В.
- Общие понятия о дифференциальных уравнениях и их решениях. Уравнения 1-го порядка: задачи Коши, теорема о существовании и единственности решения задачи Коши. Уравнения с разделяющимися переменными.
- Однородные дифференциальные уравнения первого порядка.
- Уравнения в полных дифференциалах.
- Линейные дифференциальные уравнения первого порядка. Метод Бернулли.
- Линейные дифференциальные уравнения первого порядка. Метод Лагранжа.
- Дифференциальные уравнения высших порядков: задача Коши, теорема о существовании и единственности решения задачи Коши. Решение уравнений вида
.
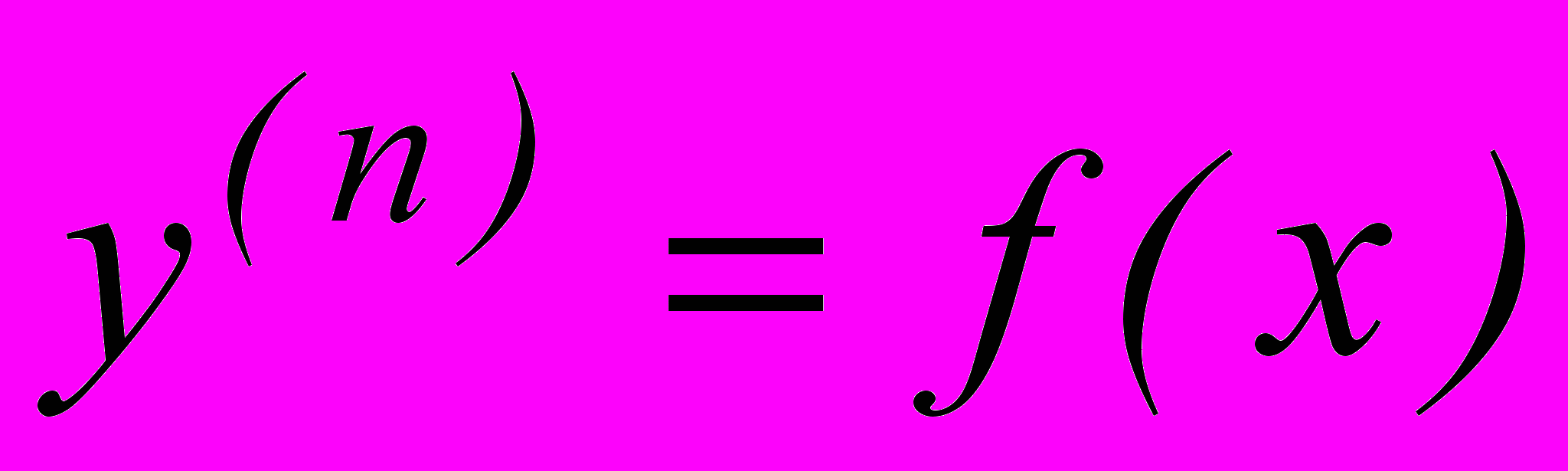- Решение дифференциальных уравнений, приводимых к уравнениям 1-го порядка (вида
, 
).
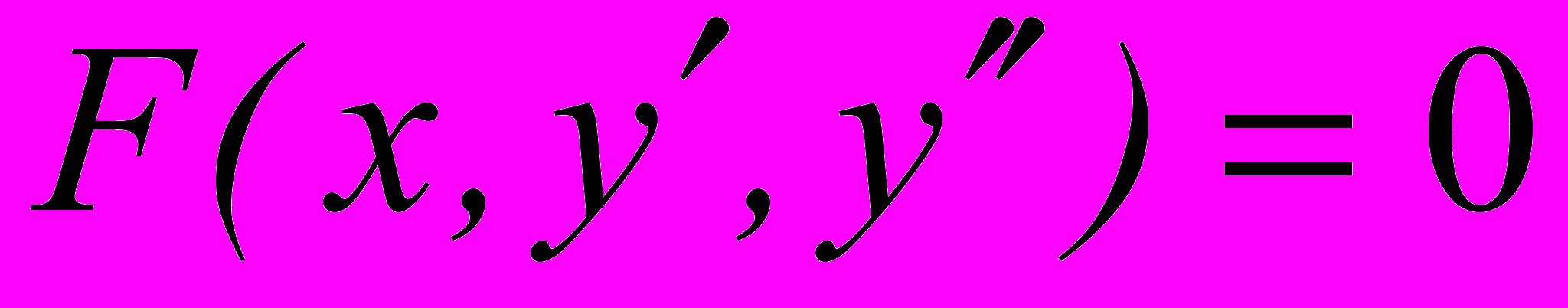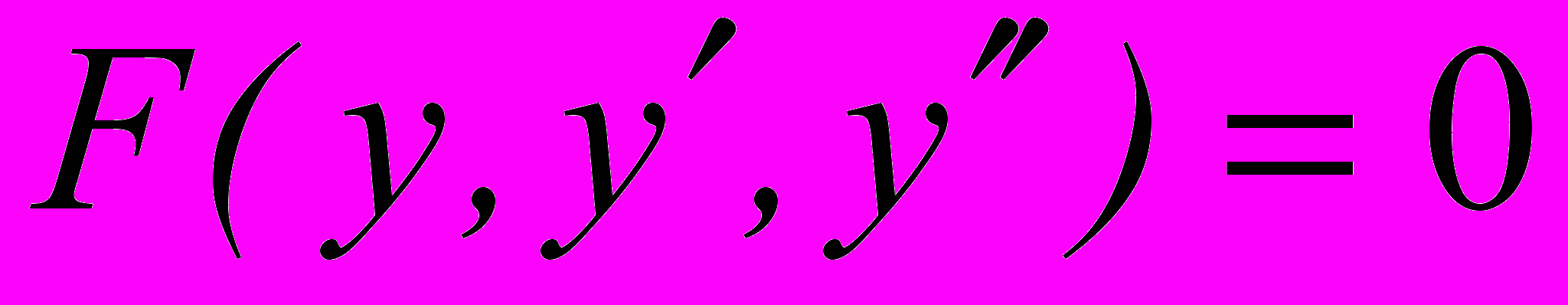- Линейно-независимые системы решений (функций). Определитель Вронского. Необходимое и достаточное условие линейной независимости решений дифференциальных уравнений второго порядка.
- Линейные однородные дифференциальные уравнения n-го порядка. Свойства их решений. Фундаментальная система решений. Структура общего решения.
- Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Построение фундаментальной системы решений.
- Неоднородные линейные дифференциальные уравнения n-го порядка. Структура общего решения.
- Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Случай, когда правая часть представляет собой показательную функцию.
- Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Случай, когда правая часть представляет собой тригонометрический полином.
- Линейные неоднородные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Случай, когда правая часть представляет собой полином, например второй степени.
- Дифференциальные уравнения, неразрешённые относительно производной.
- Понятие об интегрировании дифференциальных уравнений с помощью степенных рядов.
- Таблица производных.
- Дифференциал функции и её геометрический смысл. Применение дифференциала в приближённых вычислениях.
- Теоремы Ферма, Ролля, Лагранжа о дифференцируемых функциях.
- Теоремы Коши, Лопиталя о дифференцируемых функциях.
- Формула Тейлора. Разложение функции
, 
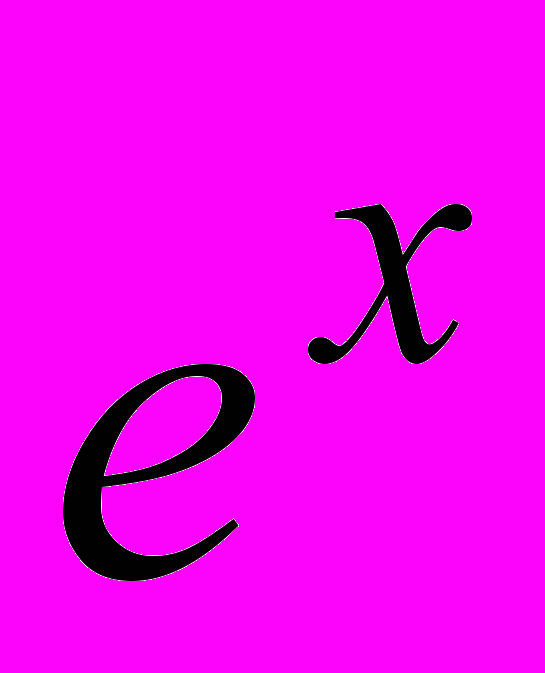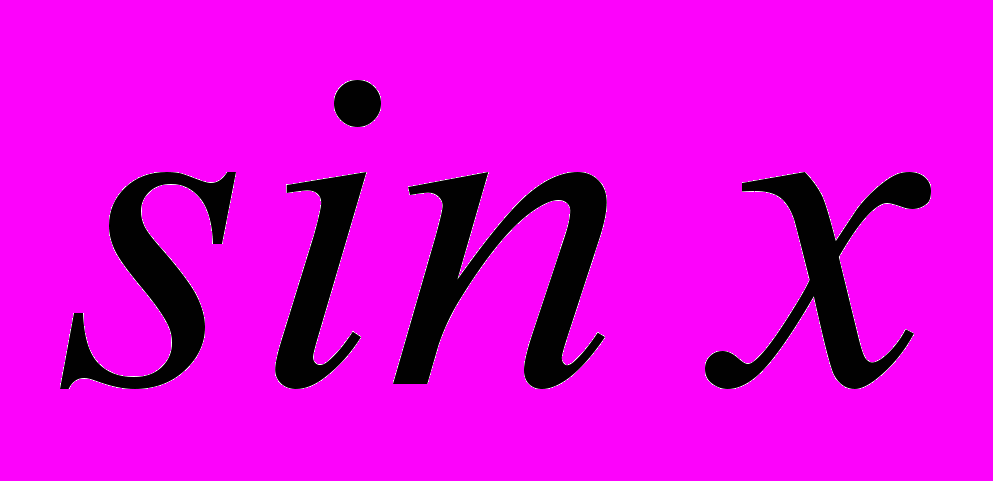в точке 
.
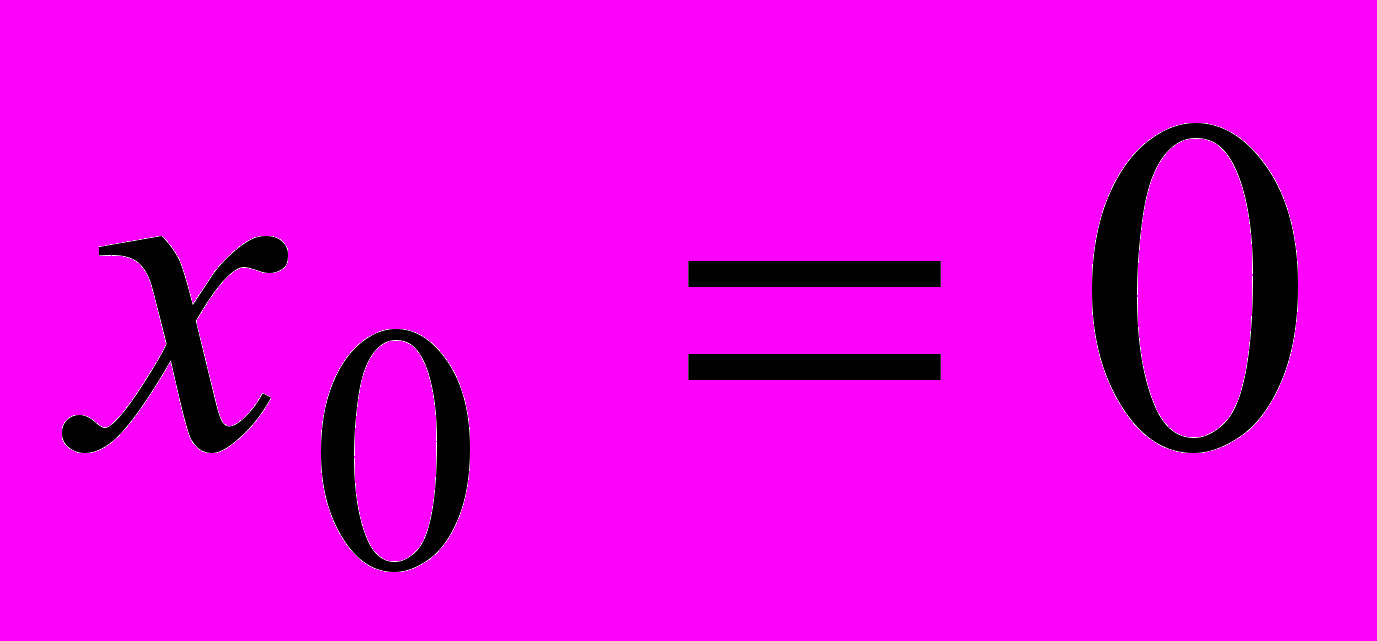- Формула Маклорена. Разложение Функций
, 
, 
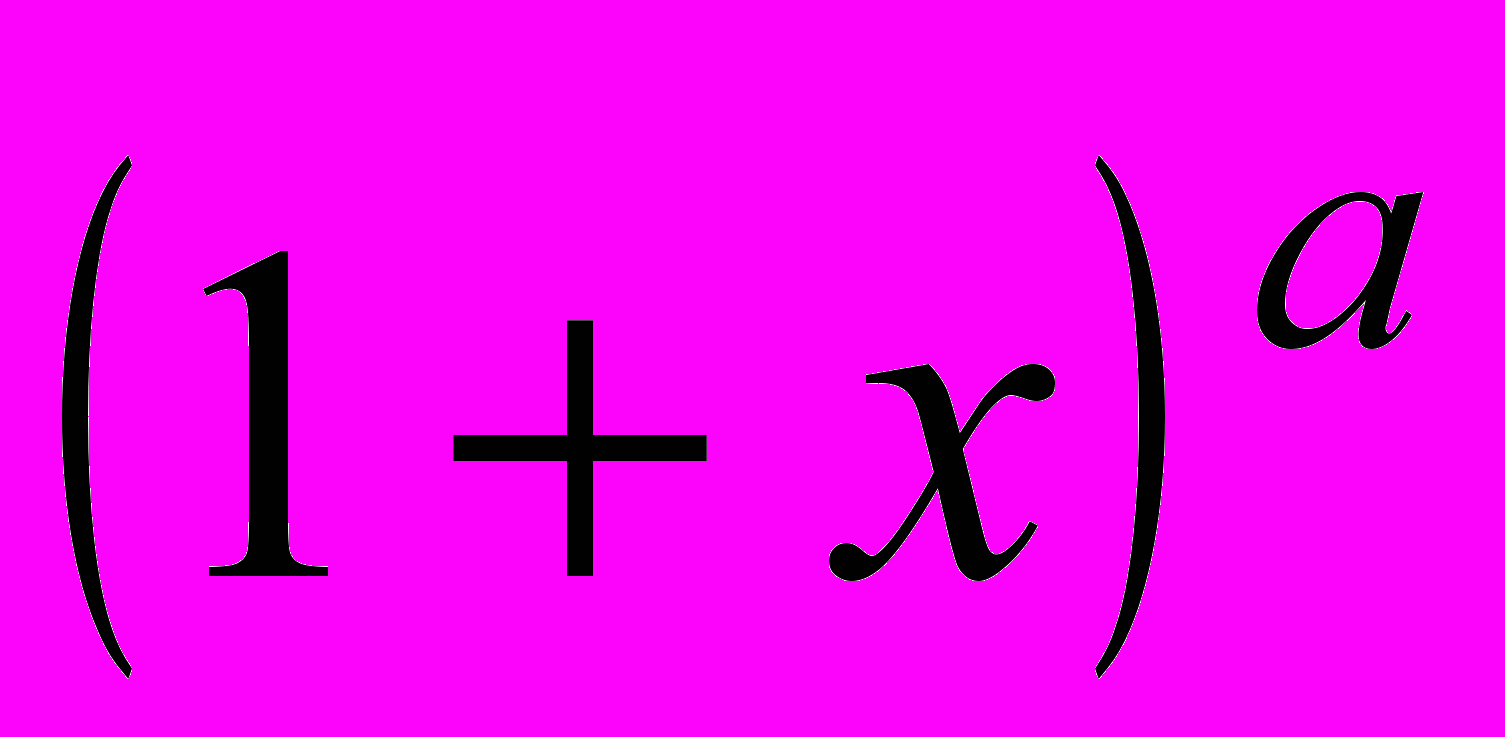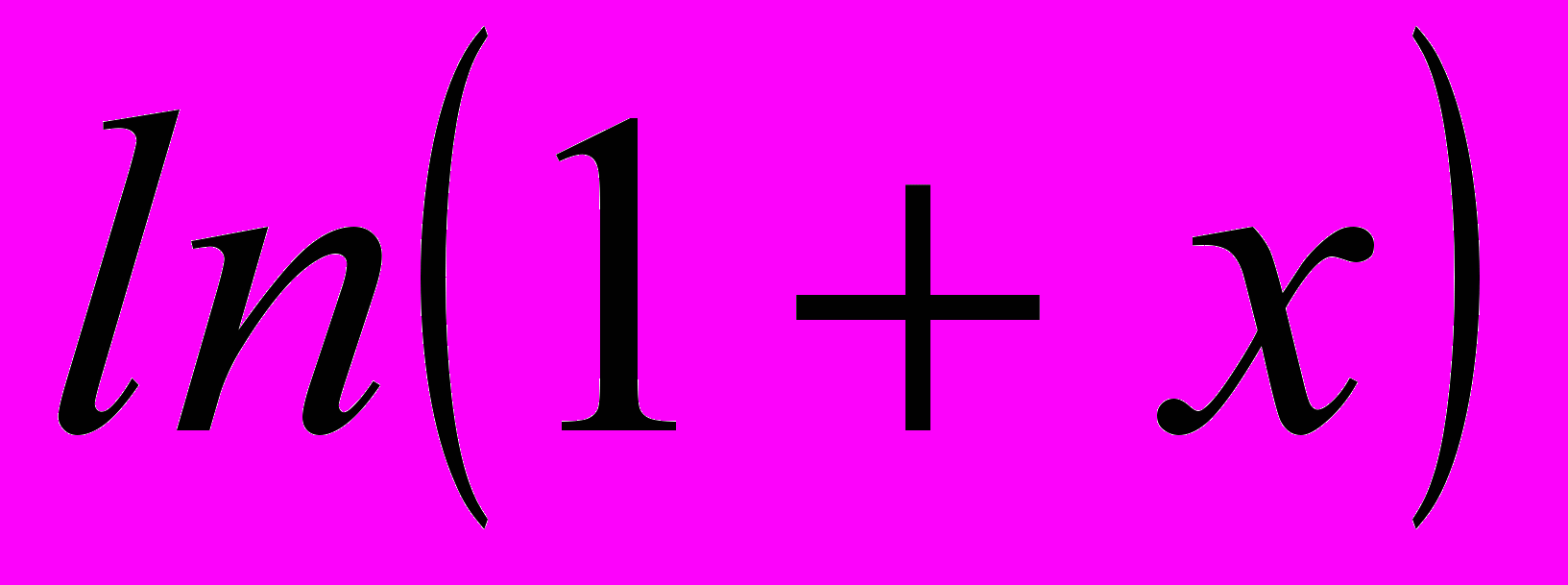по формуле Маклорена.
- Экстремумы функции. Необходимое условие существования экстремума. Наибольшее и наименьшее значения функции на отрезке.
- Экстремумы функции. Достаточное условие существования экстремума по 1-й и 2-й производной.
- Направление вогнутости графика функции. Точки перегиба. Теоремы о вогнутости и точках перегиба.
- Асимптоты графика функции.
- Полное исследование функции и построение её графика.