Контрольная работа по курсу «Высшая математика (раздел «Математическое программирование»)» для студентов заочной формы обучения и сокращенной заочной формы обучения 2 курса (четвертый семестр)

Вид материала

Контрольная работа

Подобный материал:

• Культурология рекомендации студентам заочной формы обучения. Продолжительность курса, 57.64kb.
• Методические рекомендации для студентов очно-заочной и заочной форм обучения Тематика, 268.03kb.
• Тематический план для студентов очной формы обучения Тематический план для студентов, 1529.08kb.
• Тематический план курса для студентов очно-заочной формы обучения 7 > Тематический, 1325.78kb.
• Экзамен Контрольная работа Для студентов заочной формы обучения Пояснительная записка, 240.09kb.
• Тематический план для студентов очной формы обучения 6 > Тематический план для студентов, 660.76kb.
• Методические указания по выполнению, 130.38kb.
• Методические рекомендации к выполнению курсовой работы по основам менеджмента для студентов, 236.14kb.
• Вопросы к зачету по дисциплине математическое программирование для студентов 2 курса, 25.03kb.
• Здоровье населения и пути его улучшения, 12.76kb.

КОНТРОЛЬНАЯ РАБОТА

по курсу «Высшая математика (раздел «Математическое программирование»)»

для студентов заочной формы обучения и

сокращенной заочной формы обучения 2 курса (четвертый семестр)

факультета экономики и управления


Задание 1.


Предприятие выпускает 4 вида продукции и использует 3 вида сырья. Требуется:

1. привести пример возможных значений с_j – прибыль от реализации единицы продукции j-го вида, b_i – запасы сырья i-го вида, a_ij – количество сырья i-го вида, которое требуется для изготовления единицы продукции j-го вида; i= 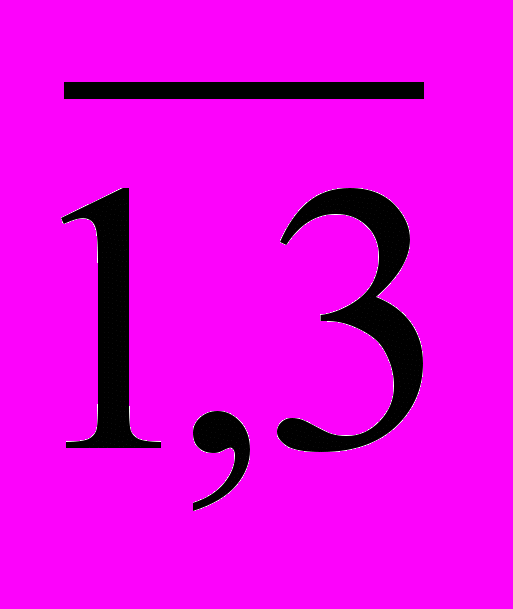, j= ;
   
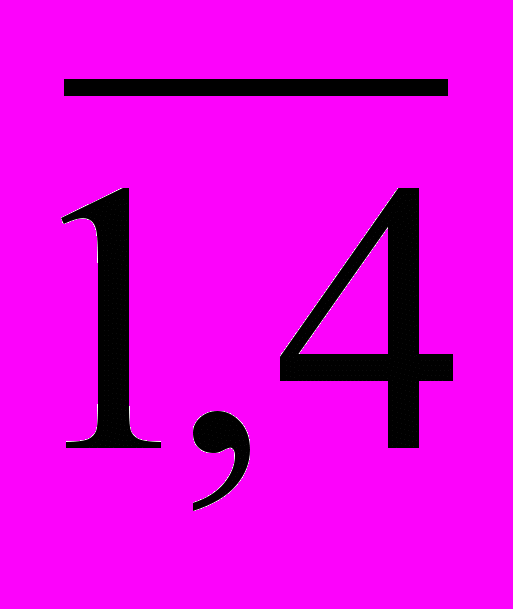2. составить математическую модель в виде задачи линейного программирования в нормальной форме;
   
3. найти оптимальный план выпуска продукции симплекс-методом;
   
4. сформулировать в экономических терминах двойственную задачу и составить ее математическую модель;
   
5. используя решение прямой задачи найти с помощью теории двойственности оптимальный план двойственной задачи.
   

Задание 2.


Задача линейного программирования имеет вид:



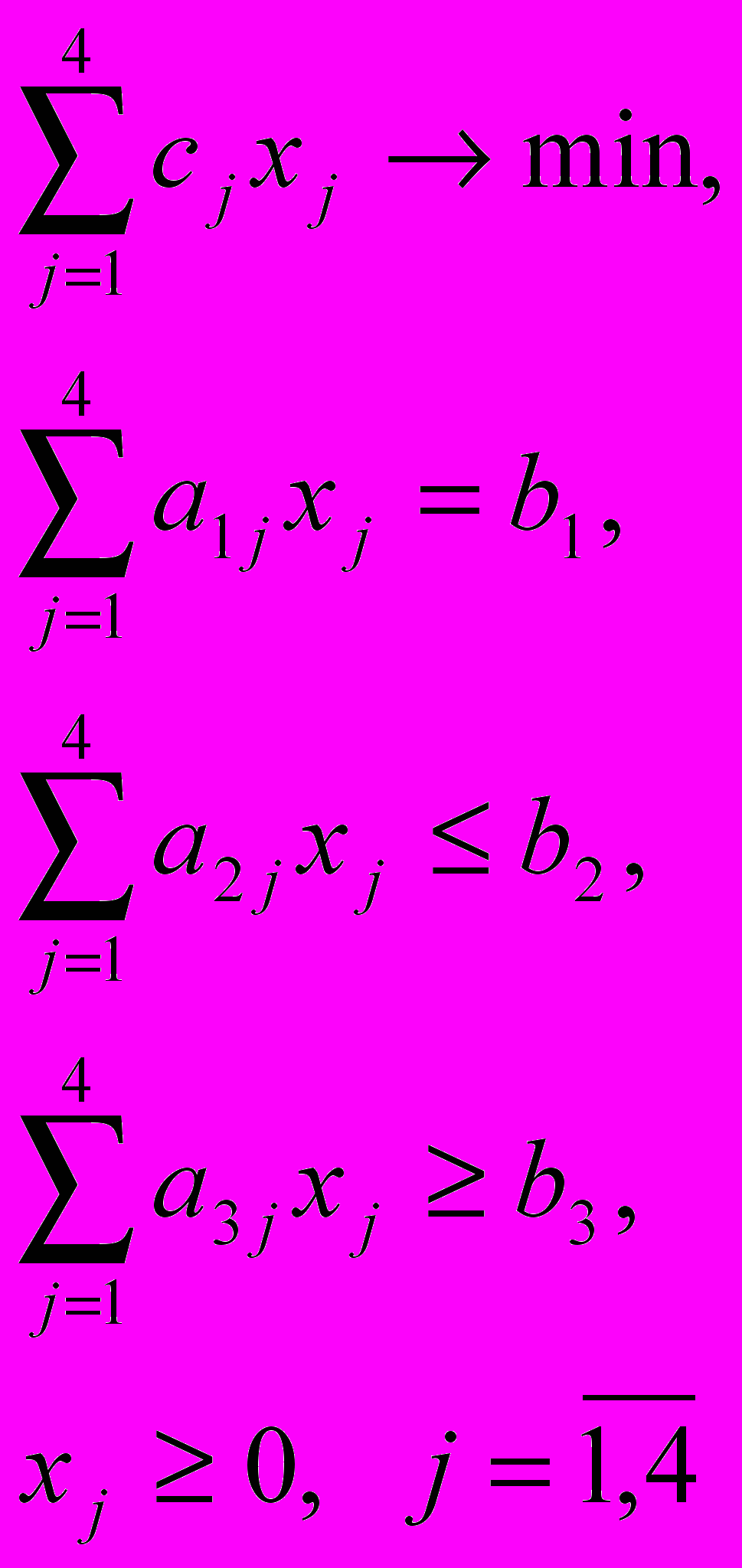
Требуется:

1. привести пример возможных значений с_j, b_i, a_ij, i= 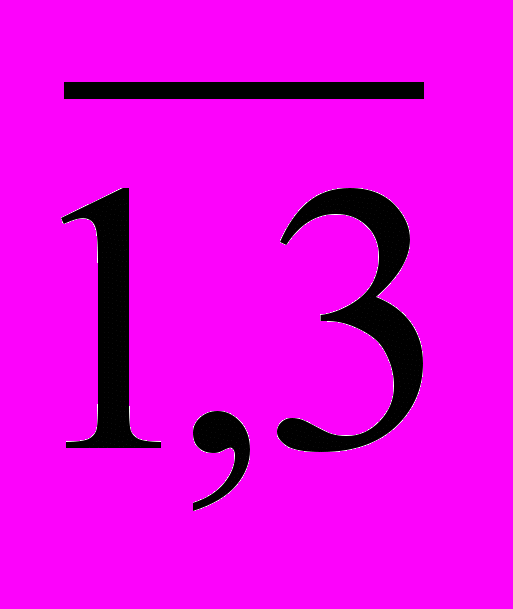, j= ;
   
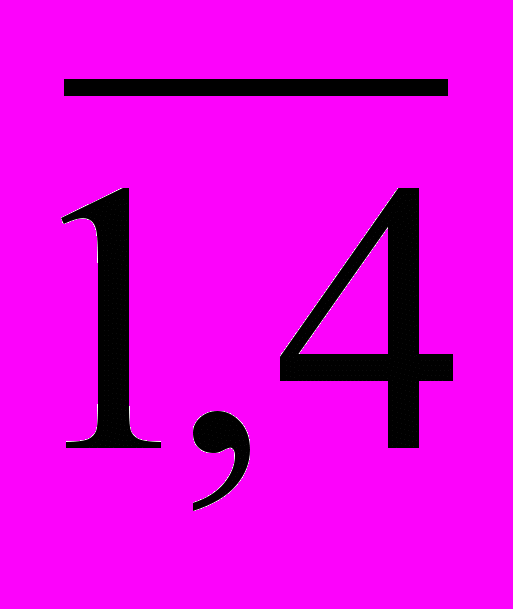2. решить полученную задачу линейного программирования;
   
3. выписать двойственную задачу;
   
4. найти решение двойственной задачи.
   

Задание 3.


Привести примеры задач линейного программирования в виде математических моделей, в которых:

а) множество планов пусто;

б) целевая функция неограниченно возрастает;

в) оптимальный план единственный.

Примеры проиллюстрировать графически.


Задание 4.


Задача линейного программирования имеет нормальный вид. Требуется:

1. привести пример возможных значений с_j, b_i, a_ij, i= 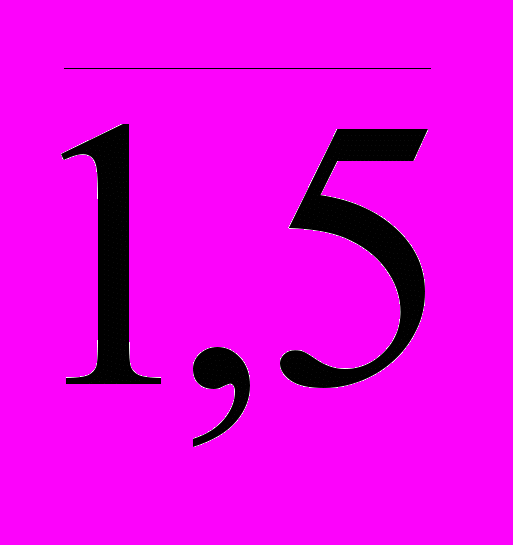, j= ;
   
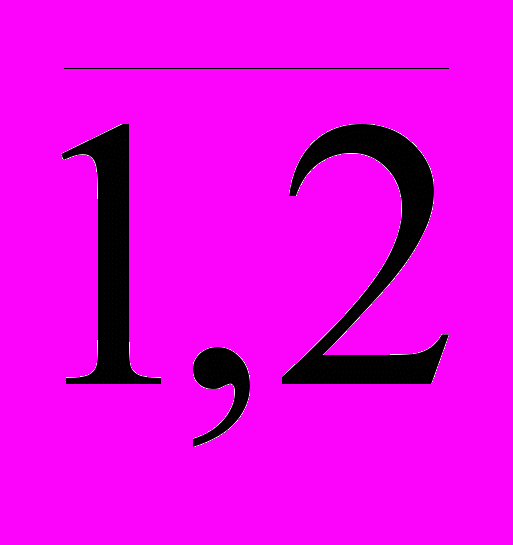2. найти оптимальный план графическим методом;
   
3. найти оптимальный план, если дополнительно задано, что все переменные целые;
   
4. решения сравнить.
   

Задание 5.


Три поставщика A_i, i=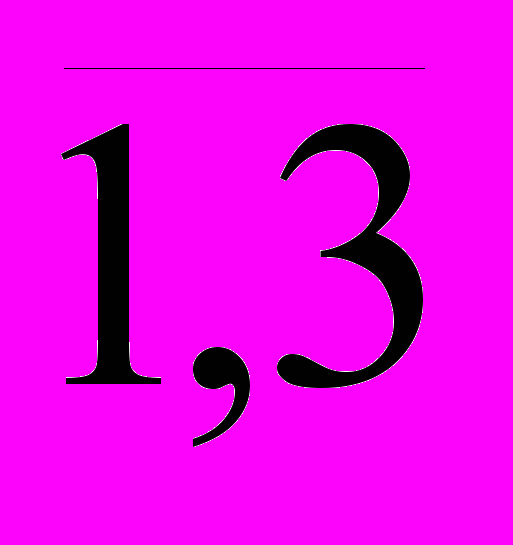, доставляют груз четырем потребителям B_j, j=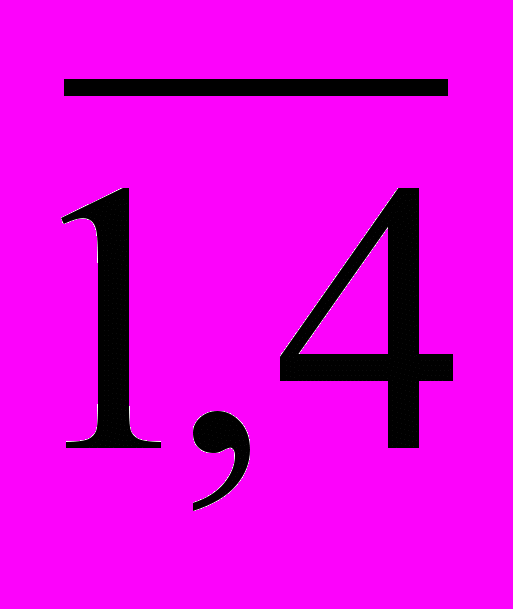. Требуется:

1. привести пример возможных значений a_i – запас груза в пункте A_i, i=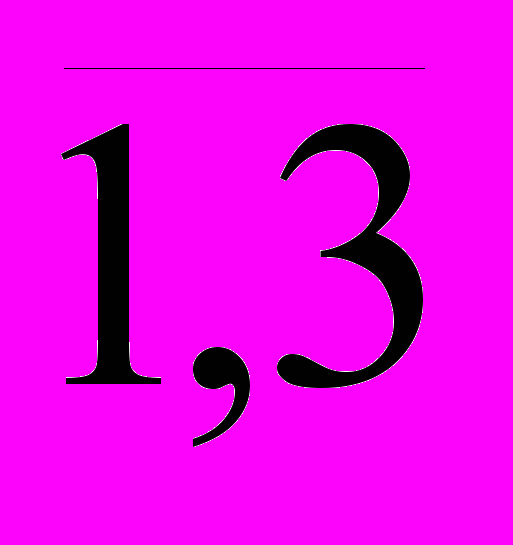; b_j – потребности в пункте B_j, j=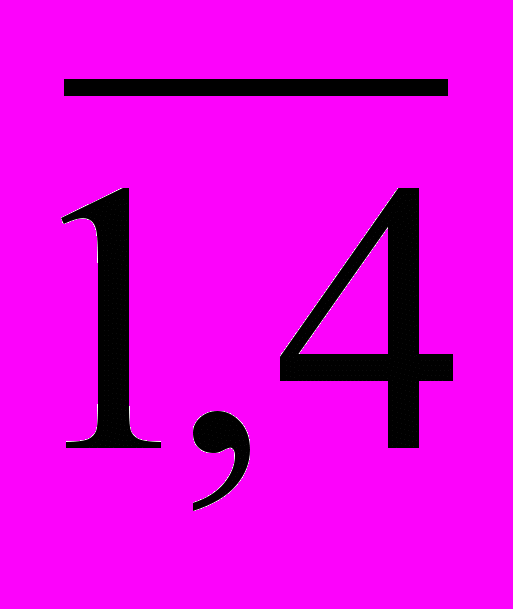; с_ij – тариф перевозки между пунктами A_i и B_j, i=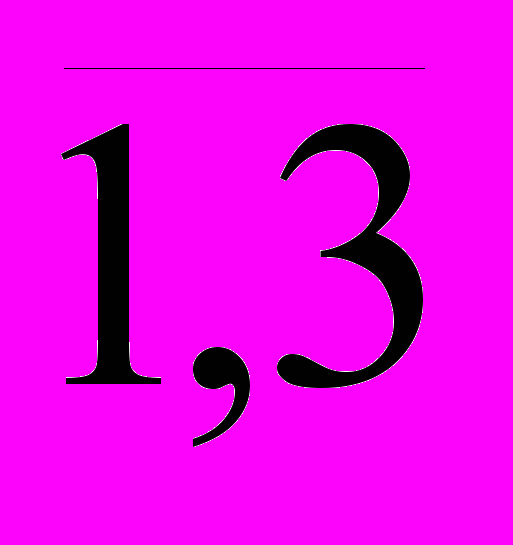, j=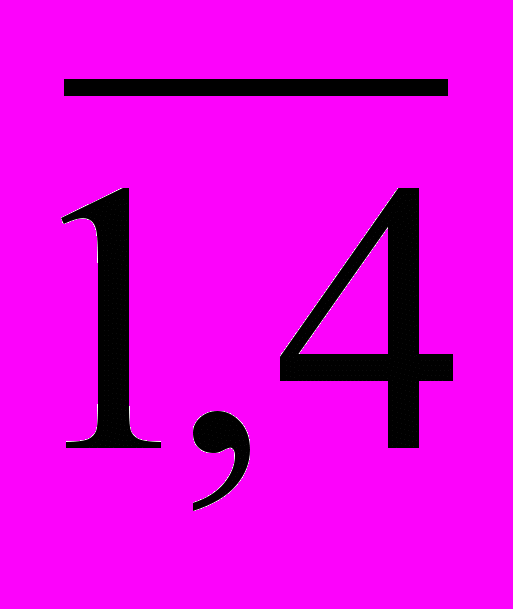; таким образом, чтобы получилась транспортная задача открытого типа;
   
2. записать математическую модель задачи перевозки груза с минимальной стоимостью;
   
3. записать задачу в табличной форме;
   
4. найти оптимальный план перевозки груза методом потенциалов.
   

Задание 6.


Сетью дорог связаны 15 пунктов. Требуется:

1. привести пример сети графически;
   
2. выбрать начальный – А и конечный – В пункты, задать затраты на перевозку единицы груза по дороге между каждыми соседним пунктами;
   
3. на основе применения метода динамического программирования найти маршрут перевозки груза из пункта А в пункт В, обеспечивающий минимальную стоимость.