Geum.ru

В. Ю. Калугина, студент; Н. Н. Михайлова, ст

Вид материалаДокументы
Подобный материал:
УДК 681.3.06

В.Ю. Калугина, студент; Н.Н. Михайлова, ст. преподаватель

Комсомольский-на-Амуре государственный технический университет


Параллельный алгоритм построения кубического сплайна


Работа посвящена распараллеливанию последовательного алгоритма построения интерполяционного кубического сплайна. Результатом является программное обеспечение, реализующее последовательный и параллельный алгоритмы построения интерполяционного кубического сплайна.

Приведем определение. Естественным интерполяционным кубическим сплайном называется функция , удовлетворяющая следующим условиям:
  1. функция – дважды непрерывно дифференцируемая функция на отрезке ;
  2. на каждом из отрезков функция является полиномом третьей степени вида

, ;
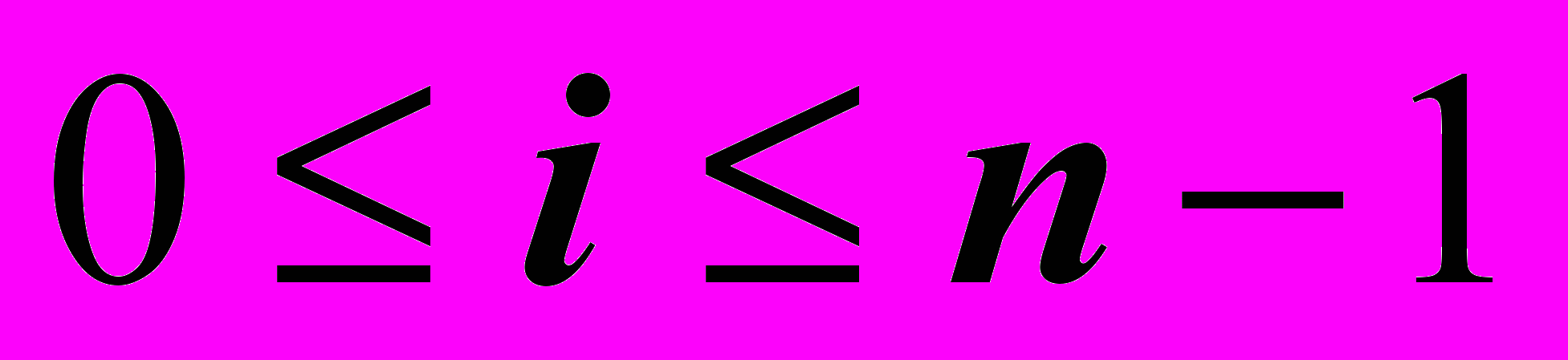  1. функция – интерполяционная функция, то есть:, ;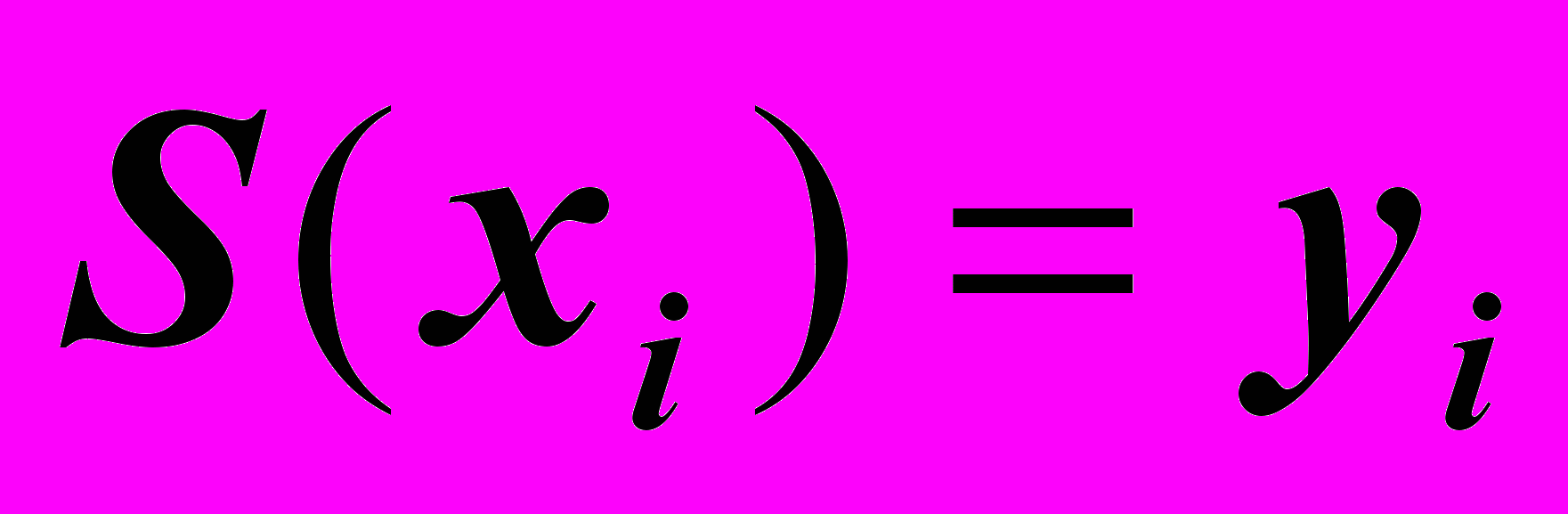

4) вторая производная функции в точках a и b обращается в ноль.

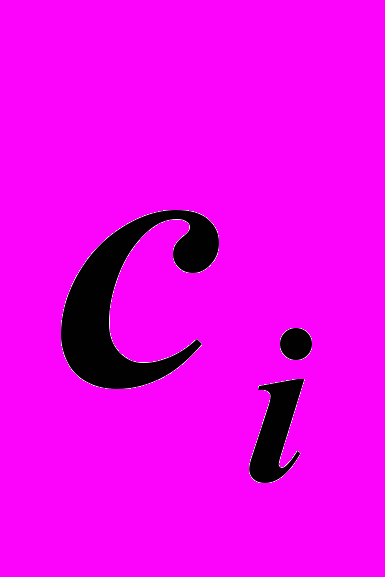
Рассмотрим алгоритм построения естественного интерполяционного кубического сплайна. Сначала необходимо найти все коэффициенты сплайна: , и , 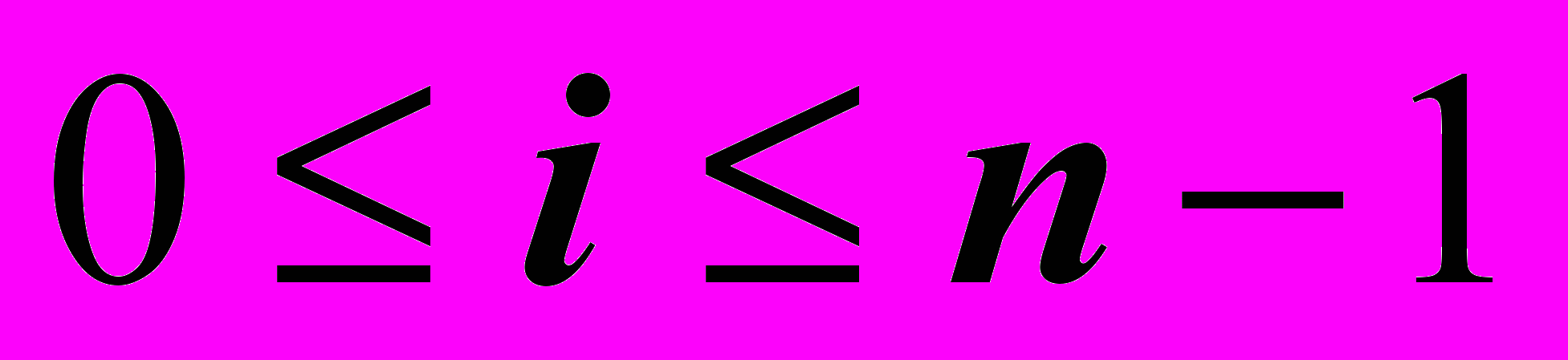. А затем, определив номер отрезка, можно вычислить значения сплайна в любой точке отрезка .

Коэффициенты сплайна находятся в следующем порядке.

1. Сначала по явным формулам находятся коэффициенты , .

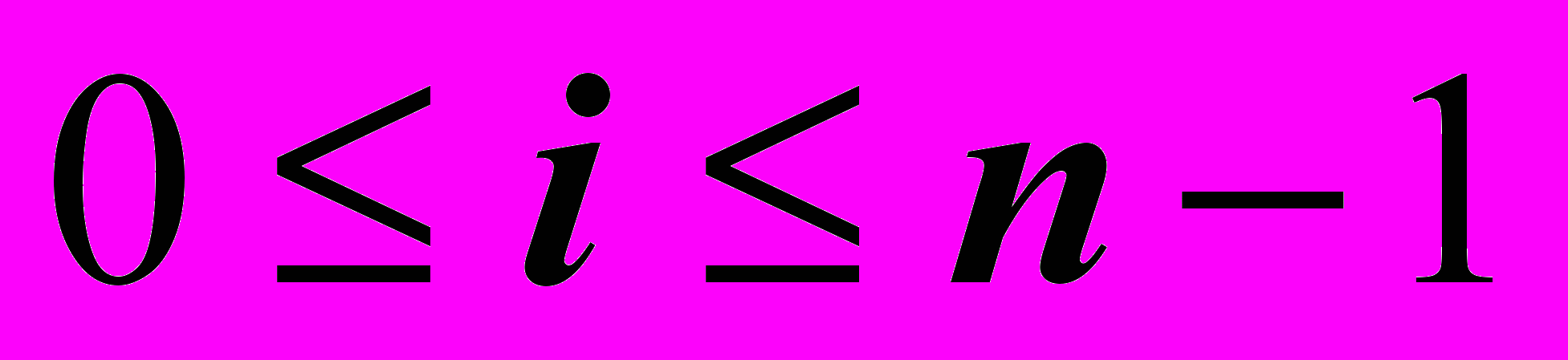2. Коэффициенты 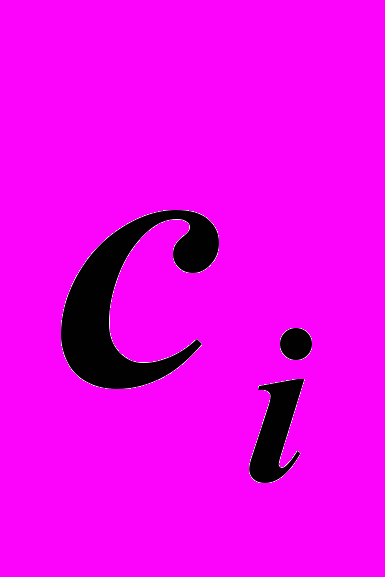находятся из решения системы линейных уравнений размерности 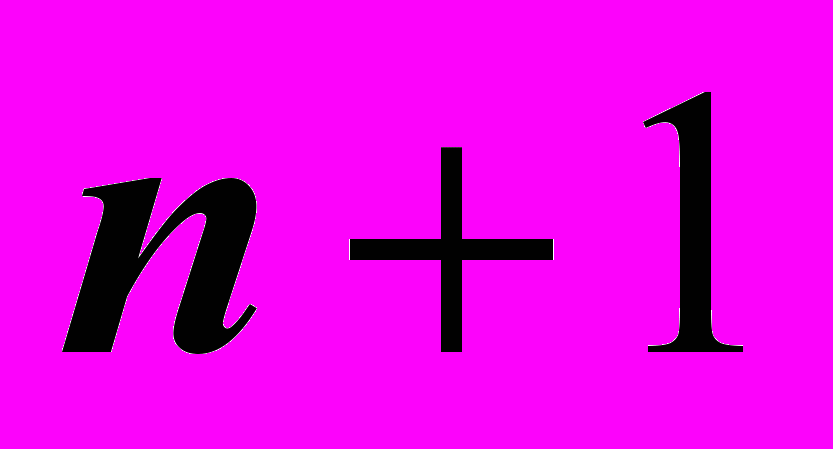с невырожденной трехдиагональной матрицей методом прогонки. Запишем эту систему линейных уравнений для случая равномерного шага


  1. Зная и 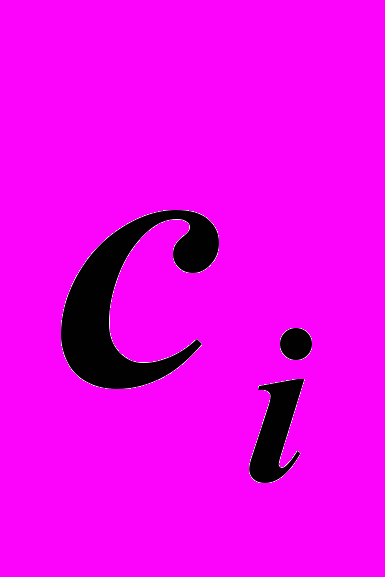, коэффициенты сплайна и можно вычислить

по явным формулам:

, , .

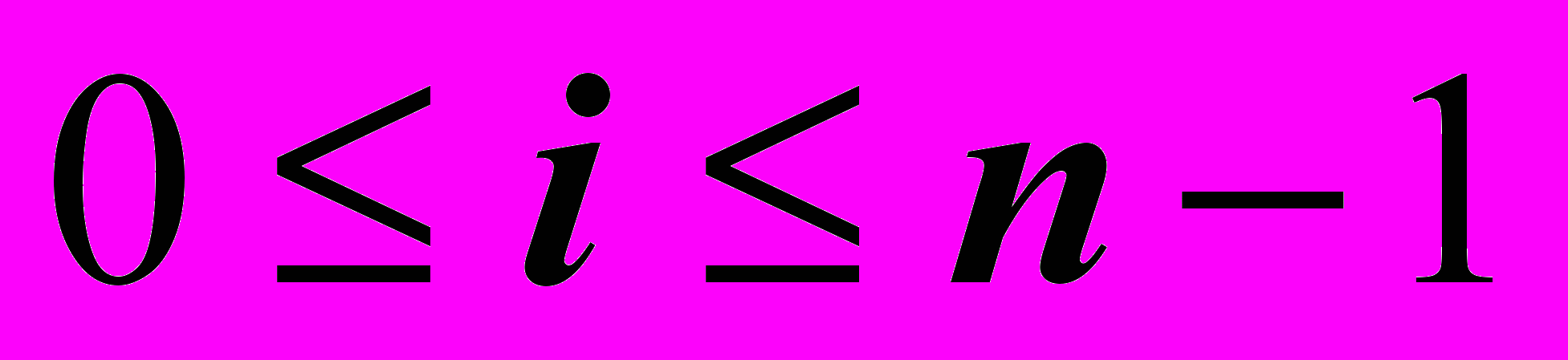Отметим, что эти вычисления можно проводить параллельно.

Обсудим возможность применения метода прогонки. Как известно, метод прогонки состоит из двух этапов. На первом, называемом прямой прогонкой, вычисляются коэффициенты 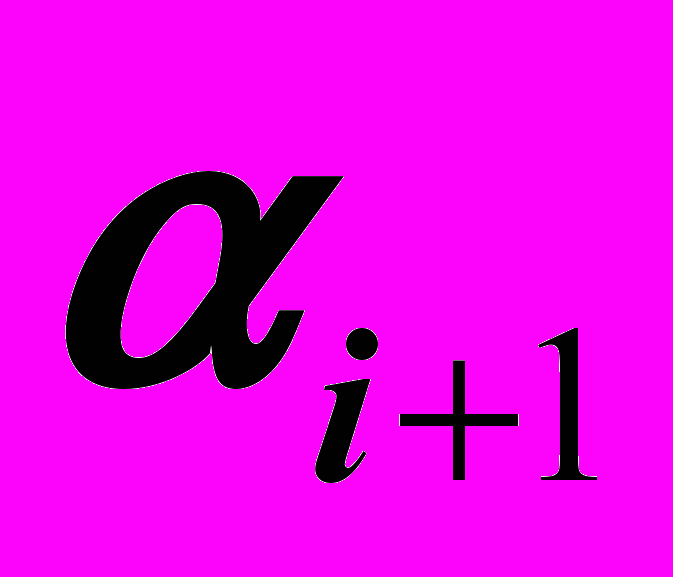, по следующим формулам:

, ,

где i= 1,2, … n-1. На втором этапе, называемом обратной прогонкой, находятся неизвестные 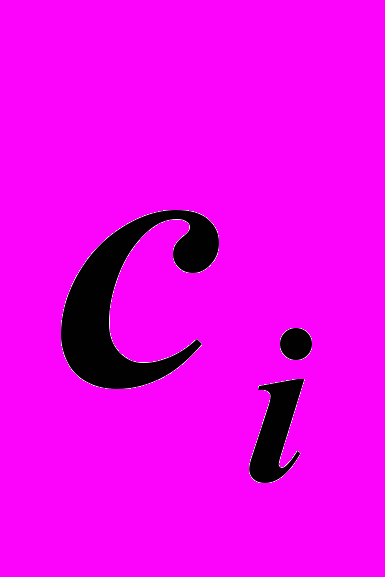в порядке убывания индексов:

,

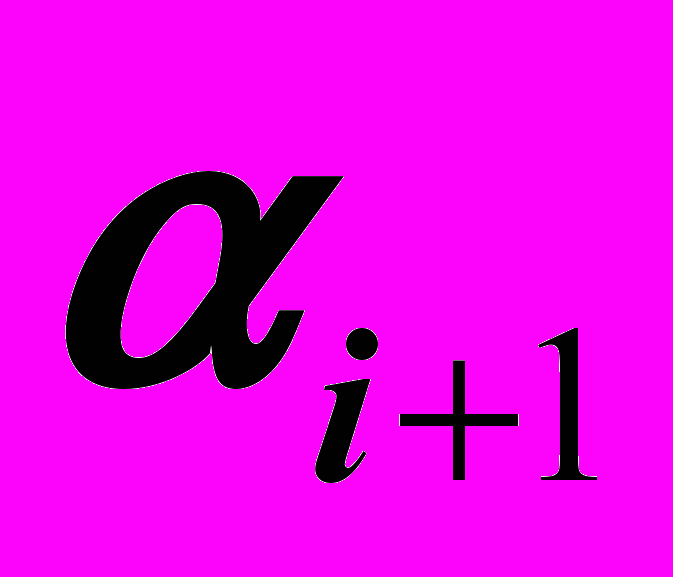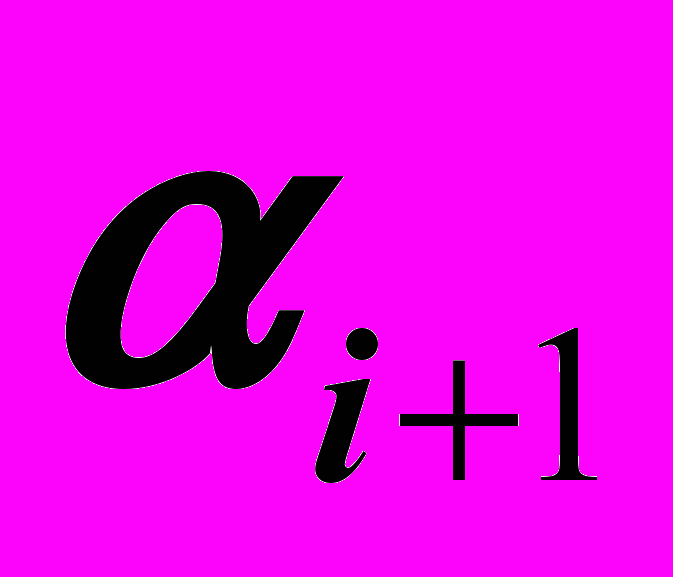Для распараллеливание метода прогонки были организованы двухпоточные вычисления. Один поток вычисляет , другой - . Т.к. при вычислении используется , то в главной программе в процессе работы запускает поток , который параллельно вычисляет 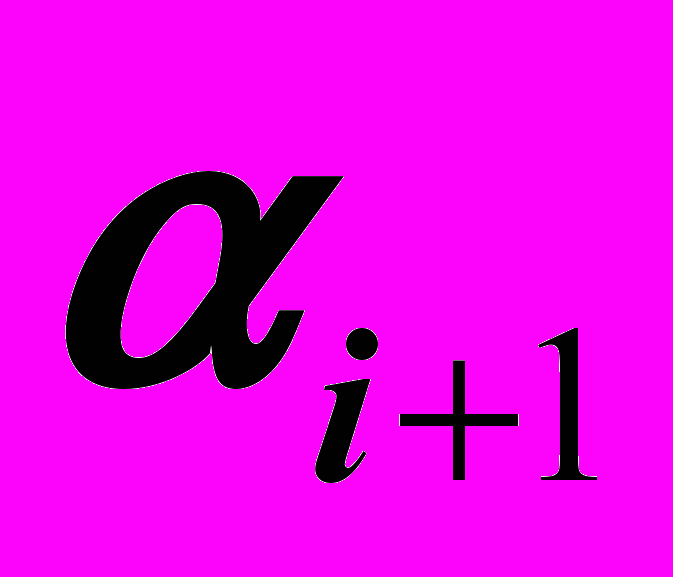. Затем, когда поступает сигнал о вычислении 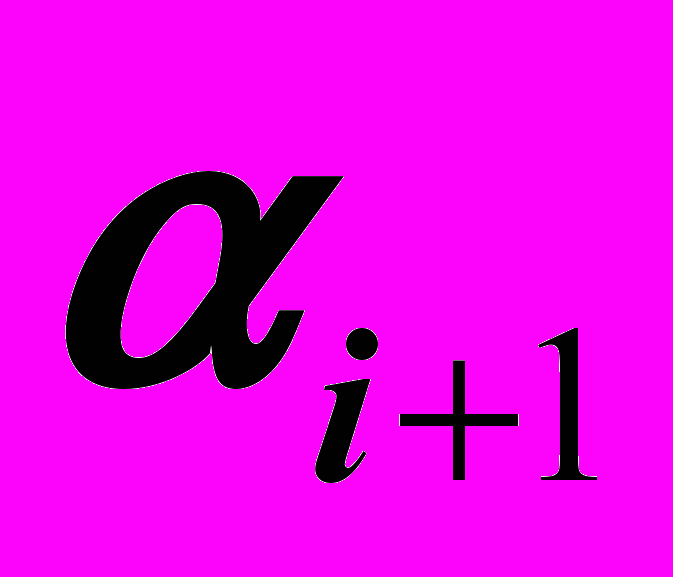, главная программа вычисляет .

При разработке параллельной программы появилась проблема. Она связана с тем, что на передачу сообщения о вычислении 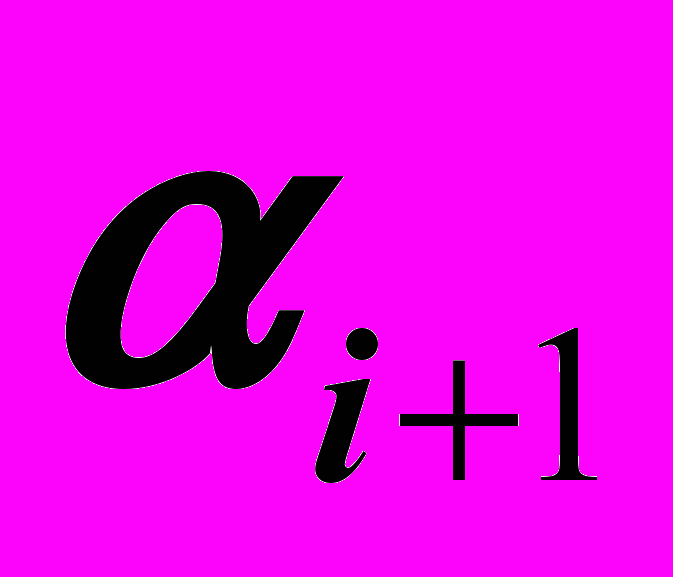расходуется времени больше, чем на само вычисление 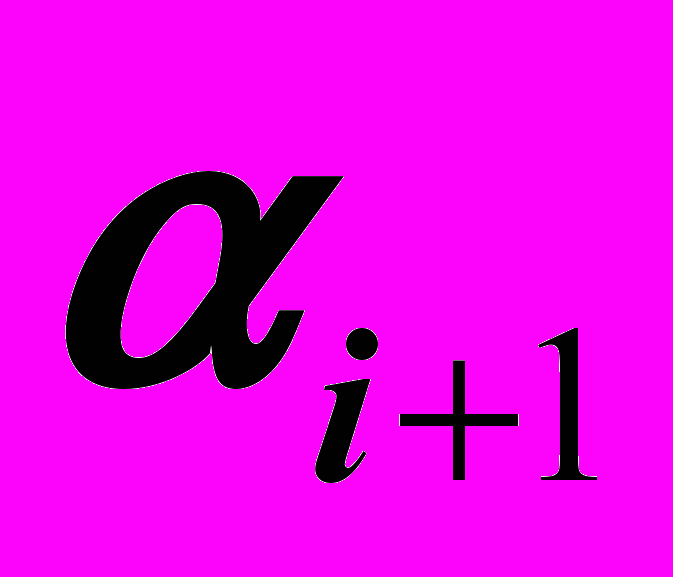. Для уменьшения времени работы параллельной программы мы предлагаем блочный подход. Заключается он в следующем. Сначала второй поток вычисляет большое количество, например тысячу, чисел 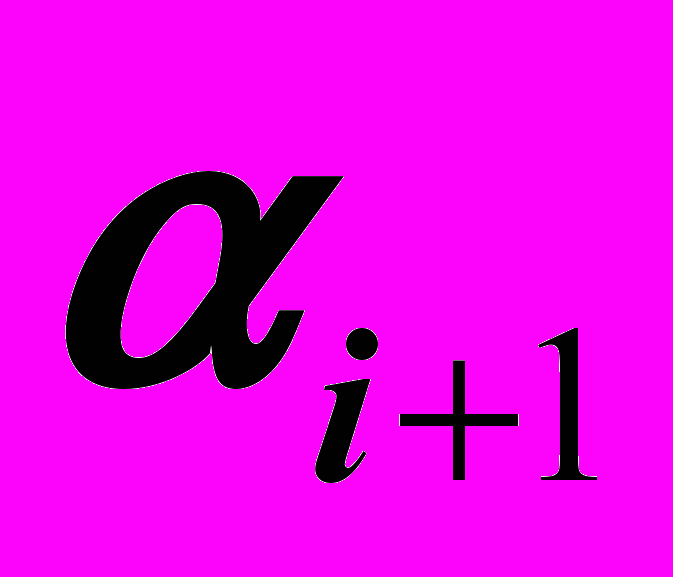. Затем он передает сигнал об их вычислении, и главный поток вычисляет тысячу , а второй поток в это время параллельно вычисляет следующую тысячу 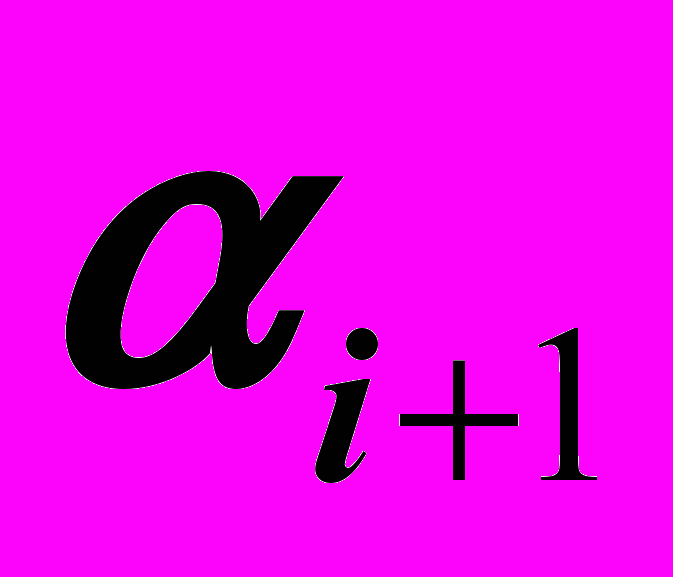. Количество вычислений внутри блока может меняться и задается пользователем.

Для распараллеливания вычислений и организуем двухпоточные вычисления. Один поток вычисляет , а второй - . Т.к. вычисления могут происходить независимо друг от друга, то эти потоки могут выполняться параллельно.

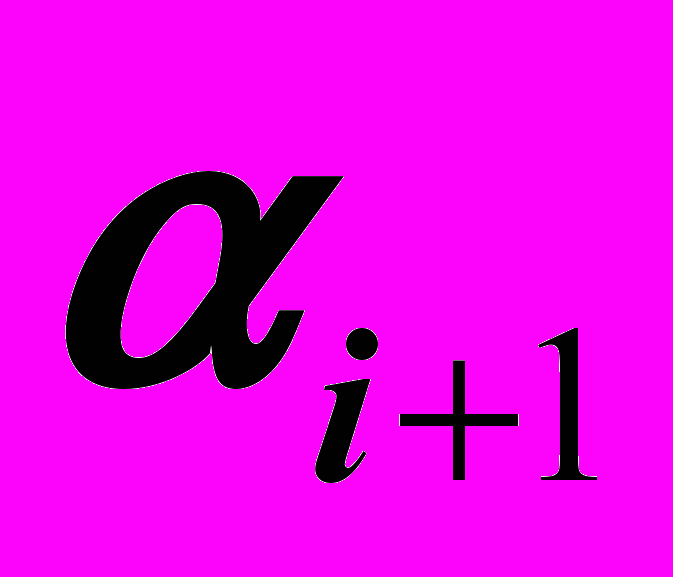Программное обеспечение было разработано на языке Borland C++ Builder 6.0 в операционной системе Windows XP. Тестирование проводилось на двухядерном компьютере Acer. При использовании блоков без распараллеливания вычислений и удалось получить ускорение от 3 до 19%. Если же использовать блоки при параллельном вычислении и и параллельно вычислять и , то удается получить ускорение до 45% (в зависимости от соотношения длины блока к числу точек).